描述刚体定点运动姿态的欧拉角作为一组广义坐标是独立的,即,任意一个欧拉角的变化不会引起其余两个的变化,并且与欧拉角相对应的转动也与顺序无关,这与通常情况下定点运动刚体的有限位移与转动顺序有关并不矛盾,或者说欧拉角对应的转动与顺序无关是一个特例。在教学过程中,导出随体坐标系到固定坐标系的变换矩阵时,往往又是规定了先进动再章动最后自转的顺序,很容易引起学生困惑：既然欧拉角的变化与顺序无关,为何这时又要规定顺序?这里,对上述问题说明以下两点：(1)欧拉角作为一组广义坐标,其与变化顺序无关;(2)将有限位移分解为三次定轴转动建立变换矩阵时,在可能的转动顺序中,存在一个特定的顺序,使得变换关系最为简单,即,按其他顺序也可以导出相同的最终变换矩阵,只是中间变换矩阵相对复杂。

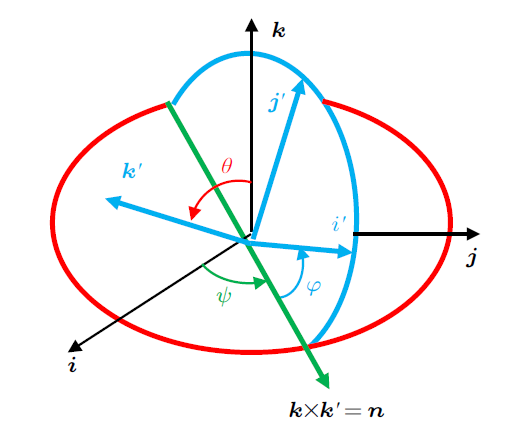
设固定坐标轴的三个单位向量为$\left( {i},{j},{k}\right)$,定点运动刚体随体坐标轴的三个单位向量为$\left({i'},{j'},{k'} \right)$,定义$n=k\times k'$,即所谓的节线方向。由此即可定义欧拉角：${k}$轴与${k'}$轴之间的夹角为章动角$\theta $,节线 ${n}$与 ${i}$ 轴之间的夹角为进动角$\psi $, ${i'}$ 轴与节线 ${n}$之间的夹角为自转角$\varphi$,如图1所示。

从图1可以看出,刚体姿态的变化可以分解为绕 ${k}$,${n}$和${k'}$三根轴的转动,不难验证,刚体绕上述三根轴中的任意一根轴做定轴转动时,仅有一个欧拉角随之变化,也就是说欧拉角是独立的;从一组欧拉角$(\psi_{0},\ \theta_{0},\ \varphi_{0})$到另一组欧拉角$(\psi_{1},\ \theta _{1}, \ \varphi_{1})$的有限位移,可以依次绕上述三根轴转动相应的角度差而实现,且与顺序无关。可以这样来理解,定点运动刚体的有限位移分解为一组定轴转动时,多种情况下是与转动顺序有关的,但是绕上述三根轴转动时与顺序无关,这也是用欧拉角作为广义坐标的必要条件。值得注意的是,当自转轴${k'}$与固定轴 ${k}$重合时,节线的方向不确定,这时刚体的运动退化为定轴转动,转角为$\beta =\psi +\varphi$,单纯从运动学上来看,在此情况下没有必要将转角分为进动和自转,一旦${k}$和${k'}$两轴分开,节线自动生成,进动角和自转角也随之确定。

用欧拉角作为广义坐标表示定点运动刚体上任意一点的位置时,通常需要导出一个从随体坐标到固定坐标的变换矩阵,导出该变换矩阵时,是按先进动$\psi$,再章动$\theta $,最后自转$\varphi$的顺序进行的,这个"顺序"似乎与第1节所讨论的欧拉角的变化与顺序无关相矛盾,下面将说明,这个顺序只是为了让每次定轴转动的变换矩阵更为简单,或者说按任何顺序都可以导出最终相同的变换矩阵,只是按不同顺序,每次转动所给出的中间变换矩阵的复杂程度不同。

为了便于讨论和欧拉角相对应的转动与顺序的无关性,以及导出随体坐标与固定坐标的变换矩阵,这里引入两个中间坐标系,设$Oxyz$为固定坐标系,其坐标轴的三个单位向量分别为$\left({i},{j},{k}\right)$,第一个中间坐标系定义为绕$z$轴做定轴转动的坐标系,其三个坐标轴的单位向量分别为$\left( {n},{k}\times {n},{k} \right)$ 如图2(a)所示,即该坐标系和固定坐标系有共同的坐标轴$z$,单位向量$n$所对应的坐标轴,也称为节线,与$x$的夹角为$\psi$,即进动角;第二个中间坐标系定义为绕节线$n$做定轴转动的坐标系,其三个坐标轴的单位向量分别为$\left({n},{k}'\times {n},{k}' \right)$,如图2(b)所示,其中,单位向量${k}'$所对应的坐标轴也称为自转轴,它与$z$轴的夹角为 $\theta $,即章动角;最后,定义随体坐标系,其三个单位向量分别为 $\left({i'},{j'},{k'} \right)$,如图2(c)所示,随体坐标系绕着${k}'$所对应的坐标轴,也称为自转轴作定轴转动,其中,${i}'$ 与节线$n$的夹角为$\varphi $,也称为自转角。

考察2.1节的四个坐标系可以发现：固定坐标系$\left({i},{j},{k} \right)$ 和中间坐标系 $\left({n},{k}\times {n},{k}\right)$之间有共同的坐标轴${k}$;两个中间坐标系$\left({n},{k}'\times {n},{k}' \right)$和$\left({n,k\times n,k}\right)$之间有共同的坐标轴${n}$;中间坐标系$\left({n},{k}'\times {n},{k}' \right)$与随体坐标系$\left( {i'},{j'},{k'} \right)$有共同的坐标轴${k'}$。上述存在共同坐标轴的坐标系之间的变换关系分别如下：

随体坐标系$\left( {i'},{j'},{k'} \right)$与中间坐标系$( n$, $k'\times n$, $k')$ 的变换关系,当随体坐标系$\left(i^{'},{j}^{'},k'\right)$上的一点,设其矢径为${r'}$,随$\left(i', j',k'\right)$绕${k'}$ 轴转过$\varphi $ 角后,该点在$\left({n},{k'}\times {n},{k'} \right)$坐标系下的矢径${r}_{k'n}$为

其中

两个中间坐标系$\left( {n},{k}\times {n},{k}\right)$和$\left( {n},{k}'\times {n},{k}'\right)$之间的变换关系,当坐标系$\left( {n},{k'}\times{n},{k'} \right)$ 上的一点,设其矢径为${r}_{k'n}$,随$\left( {n},{k}'\times{n},{k}' \right)$ 绕$n$轴转过$\theta $ 角后,该点在$\left( {n},{k}\times {n},{k}\right)$ 坐标系下的矢径${r}_{kn}$ 为

其中

中间坐标系$\left( {n},{k}\times {n},{k} \right)$和固定坐标系 $\left( {i},{j},{k} \right)$之间变换关系,当坐标系$\left( {n},{k}\times{n},{k} \right)$上的一点,设其矢径为 ${r}_{kn}$,随$\left( {n},{k}\times {n},{k} \right)$绕$z$轴转过$\psi $ 角后,该点在坐标系 $\left( {i},{j},{k}\right)$ 下的矢径 ${r}$ 为

其中

式(2),式(4),式(6)给出的变换矩阵,各对应一个欧拉角的变化,或者说,各对应一个坐标系变换矩阵,分别是随体坐标系$\left( {i'},{j'},{k'} \right)$ 到中间坐标系$\left({n},{k}'\times {n},{k}'\right)$、两个中间坐标系之间、中间坐标系$\left( {n},{k}\times{n},{k}\right)$到固定坐标系。对于给定的欧拉角,欲求刚体上一点的随体坐标与固定坐标的变换关系,可以利用上述中间变换,按"顺序"将其随体坐标逐次"过渡"到固定坐标,即,利用式(1)将随体坐标过渡到$\left( {n},{k}'\times {n},{k}' \right)$坐标,再由式(3)过渡到 $\left( {n},{k}\times{n},{k} \right)$ 坐标,最后由式(5)过渡到固定坐标系,得到

上述逐次代入的"顺序"是由四个坐标系之间的相对位置关系决定的,或者说,这四个坐标系是由三个"共同坐标轴"按"顺序"串联起来的,由此决定了上述代入顺序。这样做的目的是为了利用三次简单的中间变换,得到随体坐标到固定坐标系之间的变换矩阵$A\left( \psi \right)A\left( \theta \right)A\left( \varphi\right)$。同时,利用中间坐标系,由式(2),式(4),式(6)可以给出上述四个坐标系中任意两个坐标系之间的变换关系,例如,随体坐标系到坐标系$\left({n},{k}\times {n},{k} \right)$ 间的变换矩阵是$A\left( \theta \right)A\left( \varphi \right)$,中间坐标系 $\left({n},{k}'\times {n},{k}' \right)$到固定坐标系的变换矩阵则是$A\left( \psi \right)A\left( \theta \right)$。

将有限位移分解为定轴转动时,不引入中间坐标系,也可以在固定坐标系下直接给出每次转动以及最终位置的变换关系。例如：刚体从初始欧拉角(0,0,0)到给定欧拉角($\psi,\theta,0$)的有限位移,可以分解为两次定轴转动,如图3所示,下面我们在固定坐标系下,按两种方案分别将刚体有限位移分解为两次定轴转动,并求出刚体上的一点$M$在每次转动后的位置变化。第一种方式是从初始位置,如图3(a)所示,令刚体绕$x$轴转动角度$\theta $,如图3(b)所示,然后再绕$z$轴转动角度 $\psi $,如图3(c)所示;第二种则是先绕$z$转动角度 $\psi $,如图3(e)所示,再绕随体轴$n$转动角度$\theta $,如图3(f)所示,其中$n$ 轴在$xy$平面内,与$x$轴夹角为$\psi$。下面在固定坐标系下分析每次转动后$M$点的位置变化。

首先可以看出,两种转动方式给出的最终位置相同。第一种情况,设$M$点在固定坐标系下的初始、第一次和第二次转动后的位置向量分别为${r}_{a}$,${r}_{b}$和 ${r}_{c}$,三个位置向量之间的变换关系为：${r}_{b}=B\left( \theta\right){r}_{a}$, ${r}_{c} =B\left( \psi\right){r}_{b}$,将前面的公式代入后面可得

其中,式(8)中的两个矩阵分别与式(4),式(6)右端的矩阵相同,即,$B\left(\theta \right)= A\left( \theta \right)$, $B\left( \psi \right) =A\left( \psi \right)$,也是简单的变换矩阵。

第二种情况,由于$M$点初始和最终的位置向量和第一种情况相同,分别为${r}_{a}$和${r}_{c}$,设第一次转动后在固定坐标系下的位置向量为${r}_{d}$,有

其中,$C\left( \psi \right)$的表达式仍然与式(6)右端给出的矩阵相同,$C\left( \psi\right) =A\left( \psi \right)$。但是,当绕$n$轴做第二次转动时,$M$点的三个坐标都发生变化,同时,由于$n$轴的位置与$\psi $ 有关,变换矩阵也必将与$\psi $有关。由于在两种情况下,$M$点都是由初始位置${r}_{a}$出发,最终达到同样的位置${r}_{c}$,因此,可以利用式(8),式(9)来导出${r}_{c}$和 ${r}_{d}$ 之间的变换矩阵,求式(9)的逆有${r}_{a}=C^{-1}\left( \psi\right){r}_{d}$,将该式代入式(8)可得

从式(10)不难看出其中的变换矩阵的复杂程度。

利用式(7)也可以直接导出固定坐标系下的${r}_{c}$和${r}_{d}$之间的变换矩阵,令欧拉角为($\psi,0,0$), 由于初始位置随体坐标系与固定坐标系重合${r}_{a} =r'$,有${r}_{d}=C\left(\psi \right){r}_{a}$,或${r}_{a} =A {(\psi )}^{-1}{r}_{d}$,再令欧拉角为($\psi,\theta,0$)有${r}_{c}=A\left( \psi\right){A\left( \theta \right){r}}_{a}$,因此

本节例子说明,定轴转动刚体上任意一点的位置变化取决于轴的位置和转角,同一坐标系下,当转轴是坐标轴时,两个坐标系绕着共同坐标轴作相对转动时,变换关系最为简单。

欧拉角是一组独立的广义坐标,如果将定点运动刚体的有限位移分解为绕固定坐标系的$z$轴、随体坐标系的自转轴$z'$ 和节线 $n=k\times k'$的定轴转动,刚体的姿态变化与转动顺序无关。利用上述三根轴可以构造出两个中间坐标系,每次转动都是绕着两个坐标系的共同坐标轴进行的,因此,每次转动的变换矩阵都相对简单。给定欧拉角,确定刚体上某点的随体坐标与固定坐标的变换矩阵时,需要将三个中间变换矩阵按顺序相乘,这个顺序是由四个坐标系的位置关系决定的,即,取决于三个"共同坐标轴"串联起四个坐标系的"顺序",这个"顺序"并非是欧拉角变化必须遵循的顺序。不引入中间坐标系,也可以导出同样的随体坐标与固定坐标的变换矩阵,只是每次转动的变换关系相对复杂。