与普通小汽车相比,货车通常载重更大,重心更高。因此,货车转弯时,如果速度过大,车身会向弯道的外侧侧翻,从而导致严重的后果。因此,研究货车转弯侧翻的条件及影响因素,可以为避免侧翻事故提供理论指导。学者们对此问题已经做了一些分析^[1-5],如文献^[1]引入了横向载荷转移率作为评价侧翻的指标,并从车辆构造的角度分析了影响侧翻的因素;文献^[2]对重型货车侧翻的动力学过程进行了仿真,并提出了主动防侧翻的控制方法;文献^[5]讨论了外部条件和车体结构等多种因素对侧翻的影响,并用正交实验分析了各个因素的重要程度。

但上述文献对车辆侧翻的过程分析着力不多,大多只讨论了内侧车轮离地时对应的速度阈值。事实上,车辆侧翻是一个动态过程,内侧车轮离地并不一定导致车辆的侧翻。如果驾驶员在内侧车轮离地后及时制动,车辆仍有可能安全过弯。本文侧重研究车辆侧翻的全过程,在前人研究的基础上对车辆侧翻做进一步的分析,并讨论了不同因素对内侧车轮离地和车辆侧翻的影响。

在惯性系中,受力物体处于平衡状态的充要条件是,其受到的力系可等效为一个零力系,即外力系的主矢量和主矩均为零。众所周知,一个本身具有加速度或者角加速度的物体,并非处于平衡状态。但如果建立与一个物体本身固连的参考系,在此非惯性系下观察,物体处于虚拟的"平衡"状态。受力分析时,除真实的受力${F}$外,还需要加上非惯性系导致的惯性力——牵连惯性力${S}_{\rm e} =- m{a}_{\rm e}$和科氏惯性力${S}_{\rm c} = -m {a}_{\rm c}$,其中${a}_{\rm e}$为牵连加速度,${a}_{\rm c}$为科氏加速度。此时物体的受力可以等效成零力系,即将一个动力学问题简化为静力平衡问题求解^[6]：$F + {S}_{\rm e} + S_{\rm c}= 0$,这就是“动静法”。需要指出的是,这里研究对象是质点,如果是刚体,公式会更复杂一些。

货车转弯时,地面对车轮的摩擦力指向弯道的曲率中心,用于提供车转弯时的向心力。为保持车的力矩平衡,外侧车轮受到的支持力会大于内侧车轮,当车速过大时,将造成内侧车轮脱离地面,甚至车辆的侧翻^[1]。

对车及其运动做如下理想化假设：(1) 不考虑车的悬架结构;(2) 不考虑轮胎的形变;(3) 不计车轮的宽度;(4) 认为车的质量在车前进方向均匀分布;(5) 转弯时同侧前、后轮受力情况相同,可以等效为一个轮。

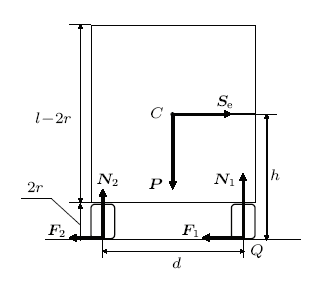
车转弯时的运动为定轴转动,转动轴过弯道的曲率中心。取与车固连的非惯性系,由动静法,假想车受到一个牵连惯性力$S_{\rm{e}}$。画出车转弯时的受力图,如图1所示。

图1中$C$为车的质心,$C$点离地高度为$h$;设轮子半径为$r$,车高为$l$,两轮间距为$d$,$Q$为转弯时外侧车轮与地面的接触点。车重为$P$,外侧车轮受到地面的支持力为$N_{1}$,静摩擦力为$F_{1}$,内侧车轮受到地面的支持力为$N_{2}$,静摩擦力为$F_{2}$。

转弯时为保持车身力矩平衡,$N_{1}$将大于$N_{2}$,且两者之差随车速的增大而增大。当车速达到某个值时,$N_{2}$减小为零,内侧车轮开始离地,我们将这一速度称为倾斜临界速度$v_{\rm{t}}$,这里的"速度"仅指速度矢量的大小,是等同于速率的标量。下面推导$v_{\rm{t}}$的表达式。

由图1中车对$Q$点力矩平衡条件,可得

令车速为$v$,转弯半径为$R$,则牵连惯性力$S_{\rm{e}} = \dfrac{Pv^{2}}{gR}$。当内侧车轮刚脱离地面时,$N_{2}=0$,代入式(1)解得倾斜临界速度

若倾斜时外侧车轮不滑动,地面摩擦力$F_{1}$需满足$F_{1}\leq f N_{1}$。由车在水平和竖直方向受力平衡,得

联立解得

内侧车轮离地后,车将开始倾斜。出于本能,此时驾驶员将会采取制动措施,降低车速。这里首先分析车在制动过程中牵连惯性力的变化。

车前进时的动能$T = \dfrac{P}{2g}v^{2}$,设制动力矩为$M$,车轮转过的角度为$\varphi$,由动能定理

由纯滚动条件$\mathrm{d}\varphi =\dfrac{v}{r}\mathrm{d}t$,代入整理得

由式(7)可知$\dot{v}$与时间$t$无关,因此车做匀减速度运动,设车入弯的速度为$v_{0}$,则$v = v_{0}-\dfrac{Mg}{Pr}t$,牵连惯性力

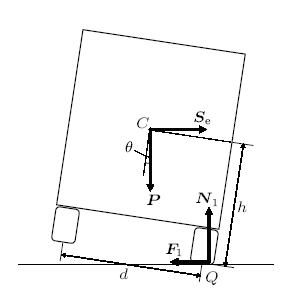
侧翻过程中,车受力情况如图2所示。

取与车的质心固连、绕弯道中心做定轴转动的非惯性系,车在此非惯性系中绕过$Q$点且与车前进方向平行的轴做定轴转动。

由对$Q$的动量矩定理,得

式中$J_{Q}$为车对$Q$的转动惯量,其计算方法如下。

将车视为重$P$的长方体,由图1可以计算得,车对通过$C$点且沿前进方向的轴的转动惯量$J_{C}=\dfrac{P}{12g}\left( d^{2}+l^{2}\right)$,由平行轴定理,对$Q$点的转动惯量$J_{Q} = J_{C} + \dfrac{P}{g}\Big[\Big(\dfrac{d}{2} \Big)^{2}+h^{2} \Big]$,整理得

若车的质心在地面的投影在$Q$点右侧,则车侧翻,即

得侧翻临界角

当$\theta > \theta _{\rm{r}}$时侧翻。若车的角速度小于等于零,且未侧翻,则安全过弯,即$\theta \leq \theta_{\rm{r}}$且$\dot{\theta }\leq 0 $。

设定货车的参数^[2-4]：$P =100$kN,$d=2$m,$h=2$m,$r=0.5$m,$M=10$kN$\cdot$m,$R=150$m,以及$ g =9.8$m/s$^2$。图中若没有特殊说明,计算中采用的参数即为以上数值。

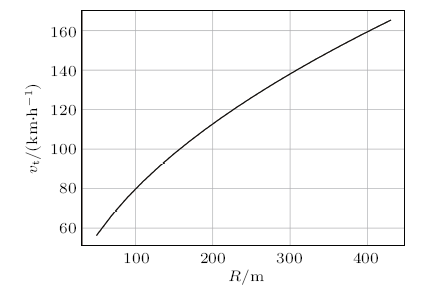
由式(2)和上述参数,可以得到倾斜临界速度$v_{\rm{t}}$与转弯半径$R$的关系曲线,如图3所示。由图可知,$v_{\rm{t}}$随$R$的减小而减小,转弯半径越小,车越容易倾斜。当转弯半径为150m左右时,倾斜临界速度已经与高速公路上的车速相近。

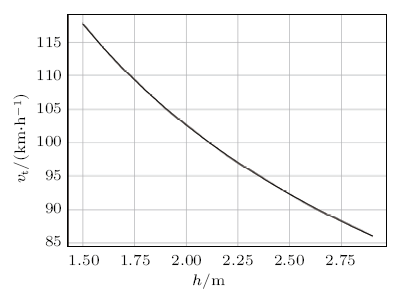
取$R=150$m,改变车的质心高度$h$,得到$v_{\rm{t}}$与$h$的关系曲线,如图4所示。由图可知,$v_{\rm{t}}$随$h$的增大而减小,质心高度越大,车越容易倾斜。

由式(5)可得摩擦系数

$$ f\geq 0.5 $$

由式(12)可得侧翻临界角

$$ \theta_{\rm{r}}\approx 26.6^{\circ} $$

若车进入弯道的速度$v_{0} \leq v_{\rm{t}}$,则车不会倾斜,因而不会侧翻;若$v_{0} > v_{\rm{t}}$,且司机不制动,则车持续向外倾斜,牵连惯性力的力矩不断增大,重力的力矩不断减小,车将加速侧翻。若车开始倾斜时驾驶员马上制动,则在$v_{0}$不太大的情况下,车有可能倾斜一定角度后摆回$\theta =0$的位置,安全过弯。我们将驾驶员制动的情况下,能使车安全过弯的$v_{0}$的最大值称为侧翻临界速度$v_{\rm{r}}$。

对于给定的初速$v_{0}$,由2.4中的分析可以计算出$\theta$随时间$t$的变化情况。编写程序计算,程序的基本思路如下：

(1) $t=0$时,设定$\theta_{0}=0$,$\dot{\theta}_{0}=0$;

(2) 在$t$时刻,由$\theta_{t}$,$S_{\rm{e}}(t)$和给定参数计算$\ddot{\theta}_{t}$;

(3) 在$t+dt$时刻,更新$\theta $和$\dot{\theta }$：$\theta_{t+dt}=\theta_{t}+\dot{\theta }_{t}dt$,$\dot{\theta}_{t+dt}=\dot{\theta}_{t}+\ddot{\theta}_{t}dt$,$t=t+dt$;

(4) 重复(2)和(3),直到车安全过弯或侧翻。

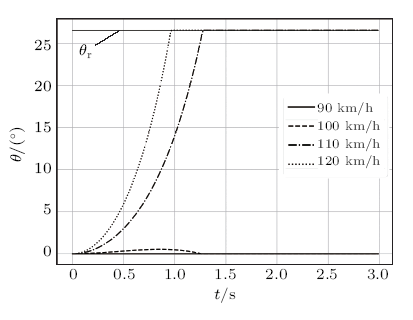
取$R=150$m,对于不同的初速$v_{0}$,计算得到$\theta$随时间$t$的变化关系,如图5所示。

由图5可知,对于不同的$v_{0}$,$\theta$的变化出现了较大的分化,当$v_{\rm{t}}\leq v_{0}\leq 100$km/h时,$\theta$先增大后减小,最终减小至零,表明车倾斜一定角度后能够回到安全状态;当$v_{0}\geq 110$km/h时,$\theta $单调递增直至$\theta _{\rm{r}}$,且$v_{0}$越大,$\theta$的增速越快,表明车不能回到安全状态,会发生侧翻。

由此可知,上述计算中的侧翻临界速度$v_{\rm{r}}$在(110km/h, 120km/h)之间,用多次迭代,两侧逼近的方法可以得到$v_{\rm{r}}$更精确的值。下面分析各个参数对$v_{\rm{r}}$的影响,并与$v_{\rm{t}}$进行比较。

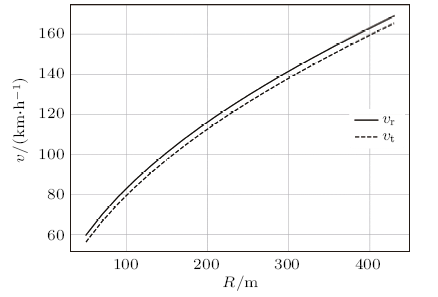
改变转弯半径$R$,固定其他参数,得到$v_{\rm{r}}$和$v_{\rm{t}}$随$R$的变化关系,如图6所示。

由图可知,随着$R$的增大,$v_{\rm{r}}$单调递增,变化与$v_{\rm{t}}$相似,值略大于$v_{\rm{t}}$,且两者之差基本保持不变。这说明对于曲率半径越小的弯道,车越容易倾斜,同时也越容易侧翻,且倾斜后发生侧翻的概率与转弯半径无关。

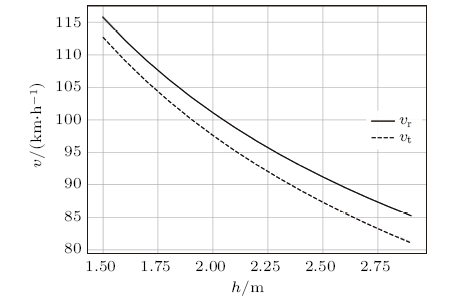
改变车的质心高度$h$,固定其他参数,得到$v_{\rm{r}}$和$v_{\rm{t}}$随$h$的变化关系,如图7所示。

由图可知,随着$P$的增大,$v_{\rm{r}}$单调递减,变化与$v_{\rm{t}}$相似,值略大于$v_{\rm{t}}$。这说明对于载重一定的货车,合理安放货物的位置,使质心的高度尽可能低,可以增大侧翻临界速度,提高车转弯时的安全性。

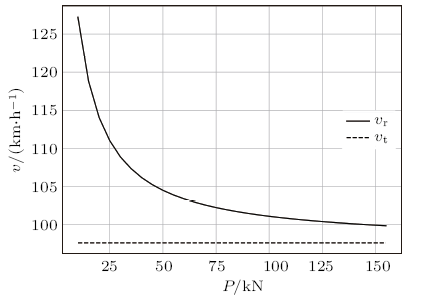
改变车重$P$,固定其他参数,得到$v_{\rm{r}}$和$v_{\rm{t}}$随$P$的变化关系,如图8所示。

由图8可知,随着$P$的增大,$v_{\rm{t}}$保持不变,$v_{\rm{r}}$类似于反比例递减,两者之差越来越小。这说明车是否会倾斜与车重无关,但减小车重能降低侧翻的可能性。车重越小,倾斜后能将车"挽救"回安全状态,避免侧翻的可能性就越大;车重越大,两个临界速度就越接近,从倾斜到侧翻的差距也越小,因此重型车的倾斜往往意味着侧翻。可见,避免超载对于保证货车的安全性非常重要。

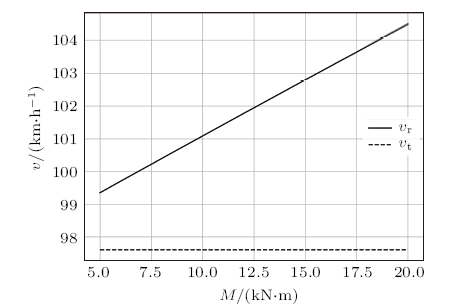
改变制动力矩$M$,固定其他参数,得到$v_{\rm{r}}$和$v_{\rm{t}}$随$M$的变化关系,如图9所示。

由图可知,$v_{\rm{t}}$与$M$无关,$v_{\rm{r}}$随$M$的增加线性增加,但变化幅度不大,这是因为从倾斜到侧翻的过程只有短短几秒,制动带来的减速效果并不明显。考虑到制动力矩的大小受到摩擦片及传动机构的限制,其对车辆防侧翻的保护很有限。因此,在入弯前降低车速比入弯后制动,对防止侧翻来说更有效。

本文利用动静法的思想,分析了货车转弯时的物理现象。货车转弯时,在与车固连的非惯性系中受到牵连惯性力的作用。当入弯车速小于倾斜临界速度($v_{0}$ < $v_{\rm{t}}$) 时,内侧车轮始终与地面接触,车不会侧翻;当入弯车速大于倾斜临界速度($v_{0}$ > $v_{\rm{t}})$时,内侧车轮会离地,车以一定角加速度开始倾斜,此时必须减速才可能避免侧翻。若开始倾斜时的车速小于侧翻临界速度($v_{0}\leq v_{\rm{r}})$,则车倾斜一定角度后能回到安全状态;反之若$v_{0} > v_{\rm{r}}$,则车必会侧翻。经分析,$v_{\rm{t}}$和$v_{\rm{r}}$均随车的质心高度的增大而减小,随转弯半径的增大而增大,$v_{\rm{t}}$与车重、制动力矩无关,$v_{\rm{r}}$ 随车重的增大而迅速减小,随制动力矩的增大而略有增大。

因此,基于本简化模型的分析结果,为避免货车转弯时侧翻,建议司机：(1)装货物时应尽可能降低车的质心高度;(2)不能超载;(3)不能超速,且低速入弯比进入弯道后再减速更安全。