气泡普遍存在于核反应堆、火箭推进燃料以及化学实验等领域采用的液体材料^[1] 中。在振动条件下,这类液体材料会呈现出复杂的非线性涡流场^[2-3],并且伴随着气泡下沉现象,该现象对材料的性能及应用会产生较大影响。比如在液体火箭燃料的早期阶段^[4],火箭起飞时的振动迫使燃料箱中的气泡下沉到容器底部,使得底部压强减小,压力传感器被触发,进而导致火箭飞行时发生爆炸现象。因此,振动液体中气泡运动规律的研究,对液态金属动力装置以及气泡下沉过程中两相流动的发展都有着重要的意义,受到越来越多国内外学者的关注。

气泡在振动液体中运动时存在临界位移$X_0$,在$X_0$以下的液体区域会发生气泡下沉现象,而火箭燃料的低压区正是气泡运动到临界位移以下时形成的。因此,对于振动液体中气泡下沉运动规律的研究,前人主要关注下沉运动过程的临界位移以及速度变化。根据流体力学原理,Sorokin等^[5-6]建立了无静压力波情况下气泡下沉效应的理论模型,并且推导出气泡在流体中运动的平均速度公式。对于气泡下沉原理的研究,Bleich和Blekhman分别从不同角度出发,分析了气泡在不可压缩无黏流体中的运动行为：Bleich^[7]根据压力梯度原理,提出气泡下沉的"波诱导机制";Blekhman等^[8-9]根据气泡压缩性原理,提出气泡下沉的"振动诱导机制"。两者的理论推导都着重强调了气泡下沉的临界位移$X_0$,但由于流体内气泡大小各异且体积形状始终发生变化,因此实验中$X_0$界线的准确测量具有一定的难度。随后Kana等^[10]对Bleich的工作进行改进,提出了气液系统的压缩性和容器壁的弹性对气泡运动的影响。Apshtein^[11]描述了液体中气泡群在垂直管内产生的垂直振荡现象,对空气进入液体的机理和单个微小气泡的行为给出了解释,研究了气泡群的空化及聚集现象,着重分析了气泡群的稳定性,最后比较了实验研究和理论计算的结果。Fritz等^[12]和Buchanan等^[13]从理论和实验方面,对气泡在振动液体中的循环迁移运动进行了分析。尤明庆^[14]提出,物体在液体中的平衡姿态与其长径比有关。因此,在分析气泡下沉过程的受力状态时,应关注气泡形变对其受力带来的影响^[15-17]。

本文采用数值模拟和实验研究相结合的方法,通过对气泡进行受力分析,研究多种振动条件下气泡下沉运动的行为特性。采用气泡压缩性原理进行理论分析,并通过实验研究不同激励振幅、频率对气泡运动过程中临界位移$X_0$以及下沉速度的影响,总结气泡在正弦振动液体中下沉运动行为的变化规律,为研究振动条件下气液两相流动提供一种思路。

通常情况下,液体内部的气泡受到浮力作用,会上升到液体表面。但当液体以特定的振幅、频率振动时,会出现"反常"现象,即液体内的气泡不再上升,而是在液体内悬浮,甚至下沉。气泡的下沉现象与通常的上升现象有所不同,该现象会对液体的物质性能及应用产生显著影响。

引发气泡下沉现象的原因主要有两个：一是压力脉动,振动过程中压力的周期性变化导致气泡在一个振动周期内的体积和形状发生变化,气泡液膜受力不平衡,当压力引起的向下加速度大于向上加速度时,气泡向下运动;二是附加质量^[18],当气泡通过流体加速时,气泡所受的推力不仅要增加气泡的动能,还要增加周围流体的动能。此时需要有大于合外力$ma$的附加力,使气泡有效质量增加,产生向下的加速度。

假设气泡为可压缩性理想气体,容器为刚性壁,且忽略气泡间的相互作用力。则气泡在振动液体中运动时,所受之力有重力、浮力、流体阻力、附加质量力以及液体正弦振动产生的脉动压力,其中,附加质量力和脉动压力的数量级较大,是影响气泡下沉的主要因素。

当气泡通过流体加速时,气泡所受的推力要增加气泡和周围流体的动能。此时需要有额外的附加质量力,置换气泡一半体积的液体,增大气泡有效质量,产生向下的加速度。而增加的这部分质量就是附加质量$m_{\rm att}$^[18]

其中,$\rho$为水的密度,$R$为气泡的半径,$\chi$为球体附加质量系数,$m_{\rm att}$为气泡附加质量,$m_{\rm f}$为气泡体积下置换的水的质量。

综合考虑气泡在振动液体中运动时所受的重力、浮力、流体阻力、附加质量力以及脉动压力,最终得气泡受力方程等式^[19]

其中,$m$为气泡质量;$m_{\rm att}$为气泡附加质量;$C$为流体阻力系数;$V(x,t)$ 为气泡体积;$A$为振幅;$\omega = 2\pi f$,$\omega $为角频率,$f$为频率。

Bleich等^[7]的理论分析建立在球形气泡的理想状况下,忽略了气泡形变对下沉运动的影响。而实际情况下,在振动液体中运动的气泡,其体积和形状会随周围压力的改变而发生明显的变化,不再为理想球形状态,会呈现椭球形或球冠形。

设气泡的体积变化为等温准静态过程,水为不可压缩性液体,因此容器内的液体均匀振动,脉动压强为$\rho xA\omega ^2\sin \omega t$且处处相等。气泡除受此脉动压强作用外,还受到大气压强$P(0,t)$、与距离$x$有关的液体压强$\rho gx$以及表面张力产生的附加压强${2\sigma}/{R}$,因此,振动液体中气泡所受总压强为

压强脉动导致气泡在一个振动周期内体积脉动变化,根据理想气体定律,此时气泡体积为

其中,$P(0,t)$为大气压强;$V(0,t)$为气泡液面处体积;$\sigma$为液体(水)表面张力系数。

气泡在实际运动中所受的黏滞力、惯性力以及表面张力对气泡形状有很大影响,因此一般情况下气泡为非球形状态。闫红杰等^[15]提出使用韦伯数($We$)表征气泡形状变化,当$We<0.02$时,气泡为球形;当$0.02< We <0.8$时,气泡为椭球形;当$We >0.8$ 时,气泡形变进一步加大。

通过数值计算,本文得出在实验振动条件下气泡的$We >0.2$,因此应考虑振动液体中气泡的体积和形状变化。使用高速摄像机拍摄,发现气泡体积越大,变形幅度越大,并且气泡随容器做似正弦运动时,其形状随$x-t$运动曲线呈现周期性变化,如图1。

当气泡运动到波腹附近,气泡上下表面压力差较大,气泡受压变化,呈椭球形状态或变形状态,如图1(a)和图1(c);当气泡运动到波节附近,气泡上下表面压力差较小,气泡受压均匀,呈球形状态,如图1(b)和图1(d)。并且气泡运动到上波腹时,其下表面逐渐凹陷,曲率半径变大,下表面处压强变小,如图1(a);气泡运动到下波腹时,其上表面逐渐凹陷,曲率半径变大,上表面处压强变小,如图 1(g)。这是由于气泡具有压缩性,当其周围涡流场变化复杂时,液膜所受表面张力不平衡,且黏滞力、惯性力有所变化,导致气泡受力不均匀,体积和形状发生脉动变化。并且实验发现气泡体积和形状的脉动与正弦激励脉动有直接关系,呈现周期性变化。

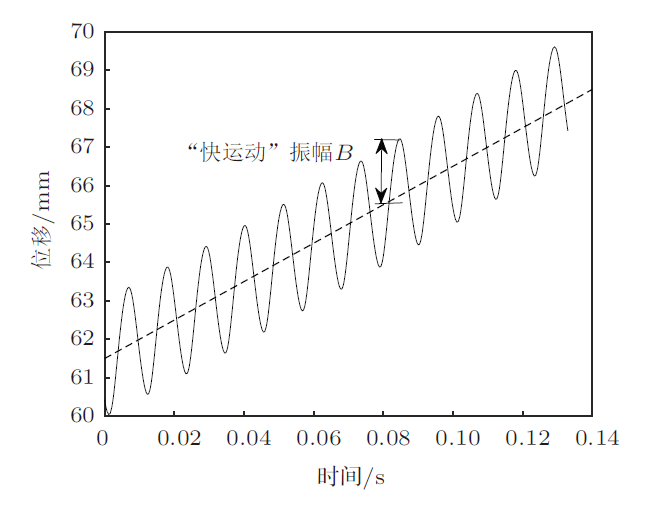
为准确表征气泡下沉运动过程,采用分离变量法对气泡运动方程(2)进行求解。求解发现气泡并非匀速或匀加速下沉而是震荡式下沉,即气泡下沉过程为时均运动(总运动趋势)以及脉动运动(正弦运动)的叠加,如图2。

以Blekhman等^[8-9]推导的"快慢运动模型"为基础,从"振动"的角度分析气泡下沉运动状态。使用振动力学的概念和运动直接分离的方法^[20],分析气泡运动行为,求出了"快慢运动"方程的解。其中,"快运动"即为气泡下沉脉动运动," 慢运动"即为气泡下沉时均运动。因此,气泡的运动方程式可写成

图2为Matlab数值模拟的气泡下沉的距离与时间的关系曲线,可见气泡在做"慢运动"下沉的同时,也在做正弦"快运动","快运动"的振幅为$B$,虚线斜率为慢运动速度$\dot{X}(t)$,并且"慢运动"决定气泡整体运动状态。

快运动方程^[20]为

其中,$m_{\rm att}$为气泡附加质量。

使用谐波平衡法可求出"快运动"方程(7)的近似解

此处$B$和$\varphi $都是常数,又因为$\big\langle {\dot {\psi}^{2}\text{sgn}\dot {\psi}} \big\rangle = 0$,因此得气泡"快运动"振幅$B$的表达式

其中,$\chi $是附加质量系数,$\psi_\infty \equiv {0.2}$。

"快运动"为气泡下沉瞬间的脉动运动,即正弦运动。气泡的"快运动"过程受外界激励振幅、激励频率的影响较大,其运动振幅$B$接近于激励振幅$A$,其运动频率与激励频率相一致。

慢运动方程^[20]为

其中,$\gamma = \dfrac{\rho H_{0} {g}}{P(0,t)}$,$H_0$为容器内液柱高度,$m_{\rm att} $为气泡附加质量。

根据式(10)可得气泡下沉的条件为

其中,$w = \dfrac{A\omega ^2}{g}$,$\theta = \dfrac{{16}^{2}}{\pi ^{4}} \cdot \dfrac{\psi^{2}_\infty}{\chi^{4}} = \dfrac{{16}^{2}}{\pi ^{4}} \cdot \dfrac{0.2^{2}}{0.5^4} = {1.68}$。 不等式(11) 的左边 是"慢运动"位移量,因此气泡是否下沉取决于其在液体的当前位置。求解不等式(11),可得气泡在特定的振幅、频率下的临界位移。

假设气泡"慢运动"加速度很小,对其"慢运动"速度,可确定以下近似表达式

其中刚性气泡"慢运动"速度的绝对值

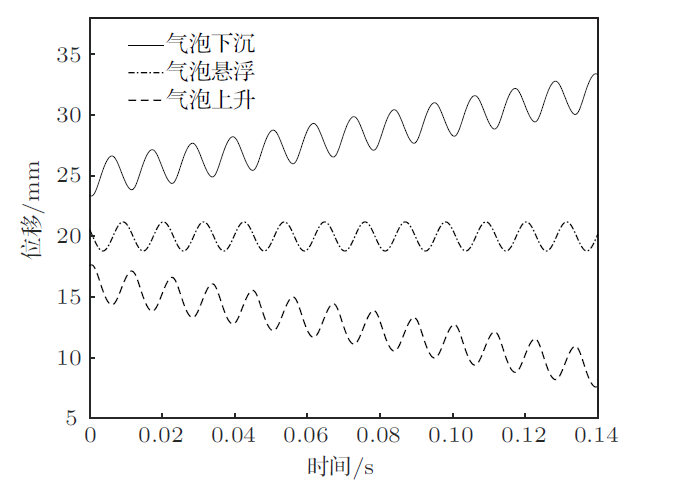
气泡"慢运动"速度的正负代表气泡的下降上升状态,如图3。当$X = X_0$时,气泡"慢运动"速度$\dot {X} = 0$,气泡悬浮在临界位移$X_0 $处;当$X < X_0$时,$\dot {X} < 0$,气泡上升;当$X > X_0 $时,$\dot {X} > 0$,气泡下沉。

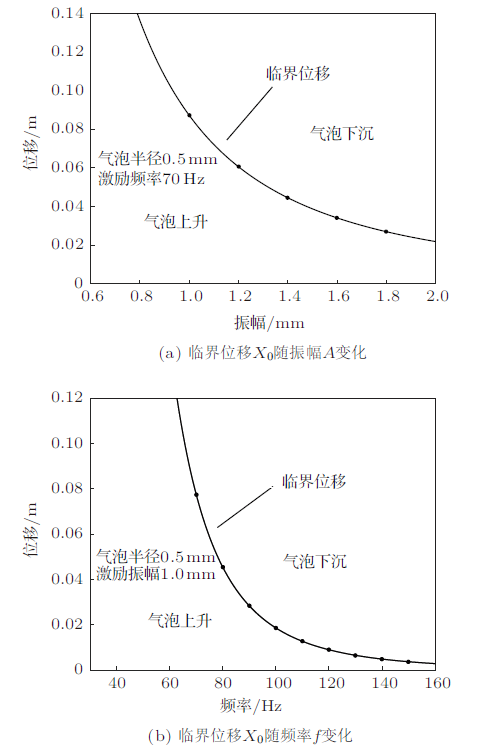
气泡是否下沉取决于位移$X$和临界位移$X_0$的关系,而根据式(12)可知外界激励振幅和频率是影响$X_0$变化的主要因素,因此,本文使用Matlab对不同振幅、频率条件下的气泡下沉运动做初步定性分析。图4(a)和图4(b)分别为临界位移$X_0$与振幅$A$、频率$f$的关系图象,可见气泡下沉的临界位移$X_0$随振幅和频率的增加而减小。并且在曲线临界位移$X_0 $以上的区域,由于$X > X_0 $,会发生气泡下沉现象;在曲线临界位移$X_0 $ 以下的区域,由于$X < X_0$,会发生气泡上升现象。

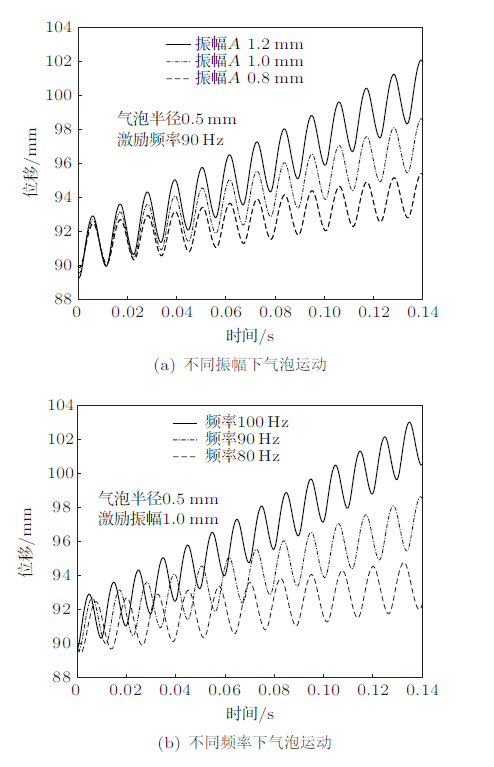
式(13)和式(14)表示,气泡下沉过程的速度取决于位移$X$和临界位移$X_{0}$的关系,并且外界激励振幅和频率影响下沉速度的大小。本文使用Matlab数值模拟不同振幅、频率下气泡下沉运动曲线,比较不同条件下气泡下沉速度大小,如图5(a)和图5(b)。

图5(a)和图5(b)分别为不同振幅、频率下气泡下沉时间-位移曲线,并且曲线的整体斜率为"慢运动"速度$\dot{X}$。由图5可见,气泡下沉的"慢运动"速度$\dot{X}$ 随振幅和频率的增加而增加。

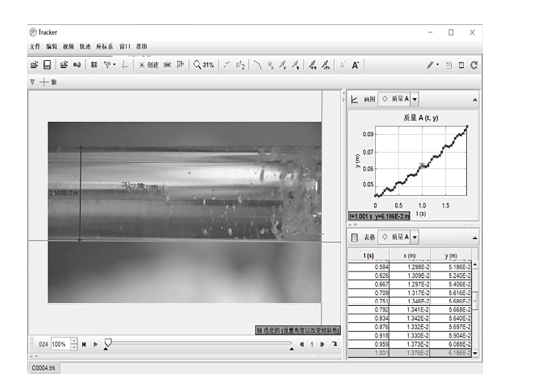
实验使用每秒240帧的高速摄像机拍摄气泡下沉运动的过程,视频导入到Tracker分析软件中,数据分析气泡下沉运动行为,如图6。

由图6可见,气泡实际运动过程与理论分析相一致,下沉过程存在"快慢运动",即气泡在做整体下沉运动的同时也做小幅度正弦振动。

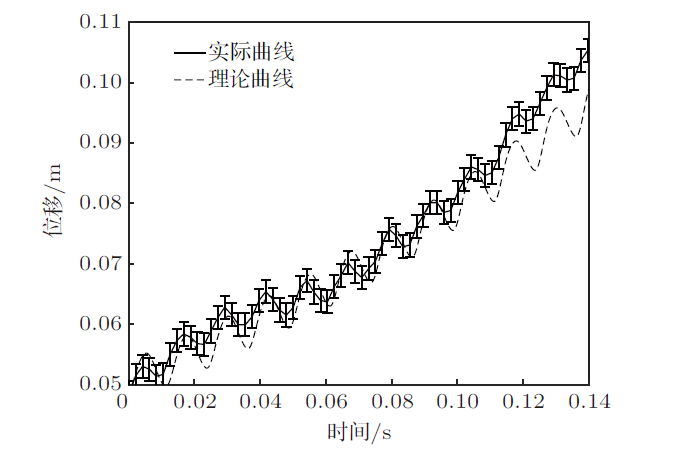
根据式(2),使用Matlab数值模拟正弦振动激励振幅2.5 mm,频率40 Hz条件下,半径为1 mm的气泡的下沉运动曲线。使用Tracker追踪半径为1.015 mm的气泡在此激励条件下的运动状态,分析实验与理论的运动轨迹,如图7所示。实验曲线大致符合理论曲线,验证了理论的正确性。

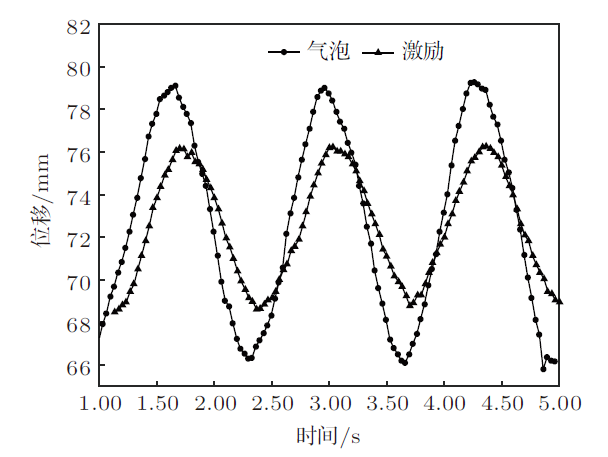
为准确追踪气泡运动轨迹,实验使用每秒960帧的慢动作拍摄,避免Tracker因取点个数太少导致误差较大。 图8为960帧慢动作拍摄下气泡和激励的运动曲线,使用Tracker 进行数据分析时发现,气泡下沉过程中气泡脉动振幅$B$大于外界激励振幅$A$,并且气泡脉动和外界激励始终存在小幅度相移差,气泡先于外界激励运动。宋禹林等^[21]在晃荡条件下气泡上升的研究中也发现了这一现象,这是因为气泡在受到外界激励的基础上,还受到来自于空气和水的密度差提供的驱动,这使得气泡所受驱动力更大,速度变化更早、更快。

初步预实验下发现,外界激励振幅越大、激励频率越高,气泡越容易发生下沉现象。

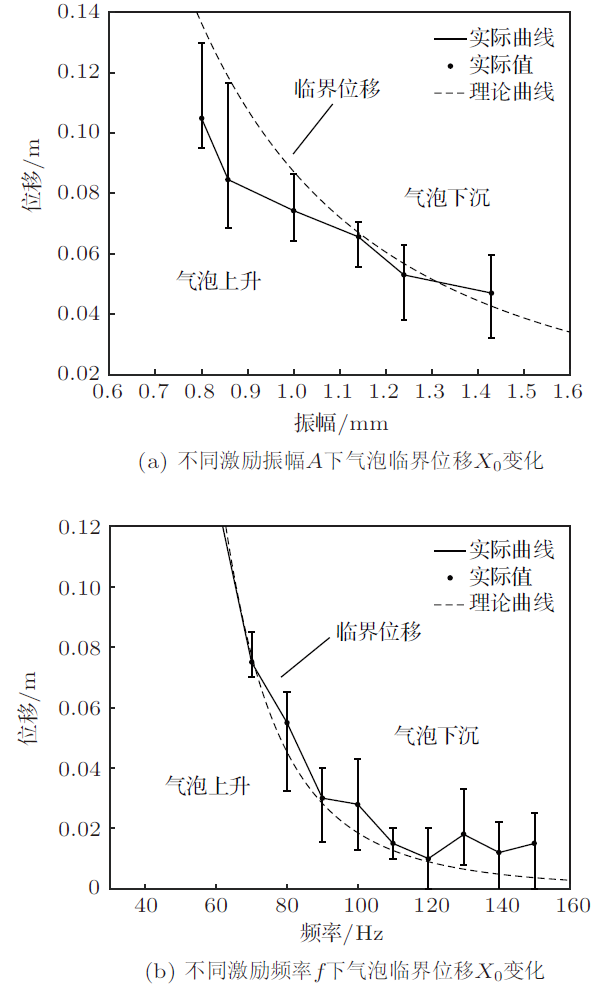
图9(a)和图 9(b)是半径为0.5 mm的气泡分别在激励频率70 Hz、激励振幅1 mm条件下临界位移$X_0$的变化曲线,并且将Matlab数值模拟公式(12)的结果与实际测量$X_0$的结果对比。由图可见,随着激励振幅、频率的变大,临界位移$X_0$明显变小。并且当振幅、频率过大时,气泡所受脉动加速度$A\omega ^2\sin \omega t$较大,因此气泡在较小的位移处会发生下沉现象。

本文从流体动力学角度分析气泡下沉现象的机理,数值模拟单个气泡在振动液体中的运动,并通过实验进一步分析气泡下沉的原因及其影响因素。对气泡进行动力学分析,研究其受力状况,得出气泡下沉的原因是压力脉动和附加质量。而压力脉动导致气泡体积脉动,因此需要考虑下降过程气泡的形变规律。采用分离变量法研究气泡运动过程,并结合Matlab数值模拟和实验测量,分析激励振幅、频率对气泡下沉过程的影响。数值模拟发现振幅、频率越大,气泡越容易下沉,且下沉的临界位移越小,下沉速度越大,这与实验测量结果一致。

实验观察到在振动的高频阶段,容器中出现大量的气泡团簇,该现象与驻波场内Bjerknes力效应导致的空泡溃灭有关,后续将对此展开深入研究。未来工作将考虑弹性壁和气泡间的相互作用,对单个气泡的分析扩展到多个气泡,并研究气泡下沉对化学仪器安全性的影响。