自工业革命以来,人类发明了内燃机、电机、气动或液压等动力装置,这些装置对人类文明的发展起到了至关重要的作用。哺乳动物则利用肌肉纤维达到驱动效果。以骨骼肌为例,其输出应力约0.3 MPa,输出应变约20%,功率密度可达300 W/kg[1 ] 。人工肌肉是指用于模仿天然肌肉的新材料或驱动装置,其可感受外部刺激(如光、电、热、湿度等)并在一个部件内收缩、膨胀或旋转,从而衍生出其他复杂类型的动作[2 -3 ] 。如何模拟动物肌肉,进而制备出先进的人工肌肉纤维,是科学家最近研究的热点问题[1 ,3 -5 ] 。2014年,Haines等[6 ] 利用聚合物纤维制作出的螺旋卷绕型纤维基人工肌肉(twisted and coiled polymer, TCP)具有如下的致动特性:当温度恒定时,肌肉相当于一个弹簧,外加载荷会导致肌肉的伸长;当温度升高时,肌肉会缩短。这种TCP人工肌肉一般由高性能纤维螺旋卷绕而成,其成本低、迟滞小、寿命长、变形量大、能量密度高,在柔性驱动技术领域具有广阔的应用前景[1 ,3 -4 ,7 ] 。
人手能够完成各种复杂的操作,但机械末端结构机械手完成这些动作并非易事。模仿人手来研究具有多关节的多指机械手的物体抓取、把持等日常动作有着重要的意义。机械手指的设计和制造核心包括执行器材料的选取、驱动方式的选择、手指驱动模型的建立等[8 -9 ] 。近年来,随着各种驱动、传感和控制技术的进步,多自由度机械手的研究也取得了较大的发展[9 -13 ] ,能够抓取各种物体。传统的机械手指多采用直流电动机、气动或液压驱动器,这些常规驱动器一般比较笨重或昂贵。目前研究人员已开始尝试采用纤维基人工肌肉驱动器、形状记忆合金等低轮廓驱动器。2016年,Arjun等[14 ] 设计了一种采用TCP人工肌肉驱动的假肢手。2017年,Wu等[9 ] 提出了一种以TCP人工肌肉为驱动的新型手指模型,通过对人工肌肉的热驱动实现手指两侧的任意偏转。他们研究了三个关节的相对偏转角$\theta_{1}$,$\theta_{2}$,$\theta_{3}$和肌肉收缩量之间的关系。随后关于这种手指实物模型的研究,大多采用Wu等[9 ] 的理论模型。但是,该模型存在的问题是模型两侧都仅采用一股人工肌肉驱动,即多个关节的偏转只对应于一个收缩量,因此,无法控制各个关节的独立转动。随后,Yip等[15 ] 在纤维基人工肌肉力与位置控制系统的基础上,通过多根人工肌肉的组合驱动,实现了仿生机械手的多指弯曲动作和手臂摆动动作。
本文旨在提出一种由TCP人工肌肉驱动的灵巧、紧凑、低成本的机械手指新模型,实现机械手指在三个自由度上的独立驱动,使其更加符合人类手指的运动学规律。同时,基于Karami等[16 ] 的热驱动物理模型,通过数值模拟对所制备的纤维基人工肌肉的热致动效果以及手指模型的偏转效果进行预测,证明纤维基人工肌肉在仿生机械手应用中的有效性。
1 手指模型
1.1 机械手指模型
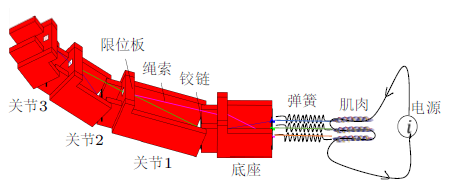
机械手指模型的结构如图1 所示,模型由三个关节和一个底座组成,关节和底座具有一沿竖直方向的限位板,关节末端用一铰链与相邻关节连接,初始时刻肌肉处于拉伸状态,随后通过电阻丝使肌肉升温,肌肉发生收缩,肌肉收缩量通过绳索传递到对应关节并转化为关节的偏转。
图1
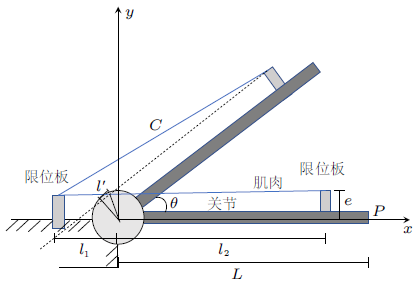
首先分析单个关节的偏转,如图2 所示,关节长度为$L$,限位板高度为$e$,长度为$d$,两侧限位板距离链杆中心的长度分别为$l_{1}$和$l_{2}$,肌肉收缩带动关节发生偏转,肌肉收缩量为$\varDelta l$,关节偏转后两限位板间的绳索长度为$C$,关节偏转角为$\theta$,关节端点为$P$。由几何关系,得
(1) $\begin{eqnarray} \varDelta l=l_{1}+l_{2}-C \end{eqnarray}$
图2
(2) $\begin{eqnarray} C=\big[(l_{1}-l')^{2}+(l_{2}-l')^{2}- 2(l_{1}-l')(l_{2}-l')\cos(\pi-\theta )\big]^{1/2} \end{eqnarray}$
其中,$l'=e\tan(\theta/2)$。偏转后,$P$点坐标为
(3) $\begin{eqnarray} x_{P}=L\cos \theta,\ \ y_{P}=L\sin \theta \end{eqnarray}$
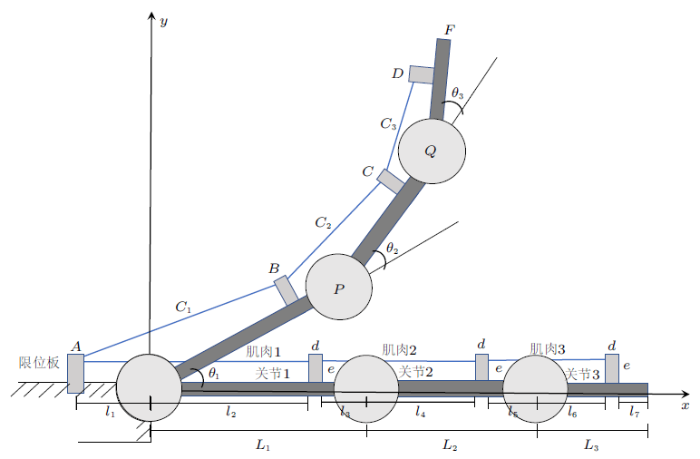
下面分析具有三个关节机械手指的偏转问题,如图3 所示。三关节机械手指的偏转可视为三个单关节偏转的组合。因此,三段肌肉的收缩量表示为
(4) $\begin{eqnarray} \left.\begin{array}{l} \varDelta L_{1}=l_{1}+l_{2}-C_{1}\\[2mm] \varDelta L_{2}=l_{3}+l_{4}-C_{2}\\[2mm] \varDelta L_{3}=l_{5}+l_{6}-C_{3} \end{array}\right\} \end{eqnarray}$
图3
(5) $\begin{eqnarray} \left.\begin{array}{l} C_{1}=\big[(l_{1}-l_{1}')^{2}+(l_{2}-l_{1}')^{2}- 2(l_{1}-l_{1}')(l_{2}-l_{1}')\cos(\pi -\theta_{1})\big]^{1/2} \\ C_{2}=\big[(l_{3}-l_{2}')^{2}+(l_{4}-l_{2}')^{2}-2(l_{3}-l_{2}')(l_{4}-l_{2}')\cos(\pi -\theta_{2})\big]^{1/2} \\ C_{3}=\big[(l_{5}-l_{3}')^{2}+(l_{6}-l_{3}')^{2}-2(l_{5}-l_{3}')(l_{6}-l_{3}')\cos(\pi -\theta_{3})\big]^{1/2} \end{array}\right\} \end{eqnarray}$
其中,$l_{i}'={e}\tan ({\theta_{i}}/{2})(i=1,2,3)$。偏转后$P$,$Q$,$F$点的坐标分别为
(6a) $\begin{eqnarray} \left[\begin{array}{c}x_{P}\\ y_{P} \end{array} \right]=\left[ {\begin{array}{*{20}c} L_{1}\cos \theta_{1}\\ L_{1}\sin \theta_{1} \end{array} } \right] \end{eqnarray}$
(6b) $\begin{eqnarray} \left[{\begin{array}{*{20}c} x_{Q}\\ y_{Q} \end{array} } \right]=\left[ {\begin{array}{*{20}c} \cos \theta_{1} & {\cos(}\theta_{1}+\theta _{2})\\ \sin \theta_{1} & \sin(\theta_{1}+\theta _{2}) \end{array} } \right]\left[ {\begin{array}{*{20}c} L_{1}\\ L_{2} \end{array} } \right] \end{eqnarray}$
(6c) $\begin{eqnarray}\left[ {\begin{array}{*{20}c} x_{F}\\ y_{F} \end{array} } \right]\!=\!\left[ {\begin{array}{*{20}c} \cos \theta_{1} & {\cos(}\theta_{1}+\theta _{2}) & {\cos(}\theta_{1}+\theta _{2}+\theta_{3})\\ \sin \theta_{1} & \sin(\theta_{1}+\theta _{2}) & \sin(\theta_{1}+\theta _{2}+\theta_{3}) \end{array} } \right]\times \left[ {\begin{array}{*{20}c} L_{1}\\ L_{2}\\ L_{3} \end{array} } \right] \end{eqnarray}$
1.2 纤维基人工肌肉热驱动模型
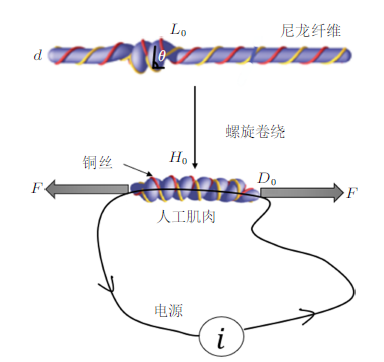
针对热驱动螺旋卷绕型纤维基人工肌肉,本文采用Karami等[16 ] 提出的物理模型。如图4 所示,单股人工肌肉表面缠绕铜丝,肌肉初始受拉伸,当$t=0$时,在铜丝中通入电流使肌肉升温,$t$时刻肌肉温度变为[16 ]
(7) $\begin{eqnarray} T=T_{0}-\frac{R_{0}i^{2}}{-hA+R_{0}i^{2}\alpha}\bigg(1-{\rm e}^{\frac{-hA+R_{0}i^{2}\alpha}{mc_{\rm p}}t}\bigg) \end{eqnarray}$
式中,$T_0$为肌肉初始时刻温度,$R_0$为铜丝电阻,$i$为通入的电流,$h$为肌肉与空气之间的对流换热系数,$A$为有效对流换热面积,$\alpha$为电阻随温度的变化系数,$m$为肌肉质量,$c_{\rm p}$为肌肉比热容。
图4
肌肉加热后收缩,肌肉最终长度为$H$,由外部载荷造成的伸长量$\varDelta_{F}$,以及加热后造成的缩短量$\varDelta_{T}$两部分叠加得到
(8) $\begin{eqnarray} H=H_{0}-\varDelta _{T}+\varDelta _{F}= H_{0}+\frac{L_{0}^{2}-\pi^{2}N^{2}D_{0}^{2}}{H_{0}}\left(c_{1}T+c_{2} \right)\left( T-T_{0}\right)+ F\frac{d^{4}{(a}_{1}T^{a_{2}}+a_{3})}{16D_{0}^{3}N(1+\mu)} \end{eqnarray}$
其中,$L_0$为尼龙纤维在室温下的长度,$d$为纤维在室温下的直径,$N$为肌肉螺旋圈数,$D_0$为肌肉在室温下的线圈直径,$H_0$为肌肉在室温下的长度,$c_{1}$和$c_{2}$为纤维轴向与横向热膨胀系数随温度的变化系数,$a_{1}$, $a_{2}$, $a_{3}$为纤维弹性模量随温度的变化系数,$\mu$为尼龙纤维的泊松比,$F$为恒定的外加载荷。
由于在机械手指中,采用了弹簧提供的线性回复力作为肌肉的外载,所以下面考虑外载形式为线性回复力时的人工肌肉热驱动模型。忽略关节之间的摩擦,认为在肌肉升温过程中,机械手指模型处于平衡状态。初始时刻,肌肉在弹簧作用下处于张紧状态,弹簧拉力为$F_0$,初始温度为$T_0$,肌肉的初始伸长量$\varDelta H_{\rm ini}$为
(9) $\begin{eqnarray} \varDelta H_{\rm ini}=\frac{16D_{0}^{3}N(1+\mu )F_{0}}{d^{4}{(a}_{1}T_{0}^{a_{2}}+a_{3})} \end{eqnarray}$
加热后,肌肉温度升高到$T$,肌肉收缩拉动绳与弹簧,弹簧刚度系数为$k_0$,肌肉在加热后的伸长量可计算为
(10) $\begin{eqnarray} \varDelta H_{{\rm end}}=\left[ F_{0}+k_{0}(\varDelta H_{\rm ini}-\varDelta H_{{\rm end}})\right]\times\\ \frac{d^{4}{(a}_{1}T^{a_{2}}+a_{3})}{16D_{0}^{3}N(1+\mu )}+ \frac{L_{0}^{2}-\pi^{2}N^{2}D_{0}^{2}}{H_{0}}\times\\ (c_{1}T+c_{2})(T-T_{0}) \end{eqnarray}$
由于$\varDelta H_{\rm ini}$和$\varDelta H_{\rm end}$都是肌肉相对于自由状态下的伸长量,所以温度升高后肌肉最终长度$H$为
(11) $\begin{eqnarray} H=H_{0}+\varDelta H_{\rm ini}-\varDelta H_{{\rm end}}=fun(T) \end{eqnarray}$
其中,$fun(T)$表示肌肉的最终长度为温度$T$的单值函数。
2 结果与讨论
2.1 热驱动型人工肌肉的致动分析
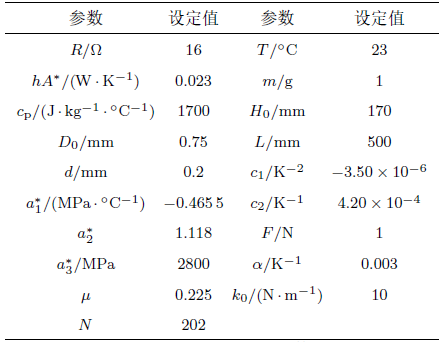
基于对文献[16 ]中实验数据的分析,给出用于模拟温度变化时肌肉收缩量的材料参数,如表1 所示。采用这些材料、结构和环境参数,对温度变化时肌肉的收缩量进行分析。
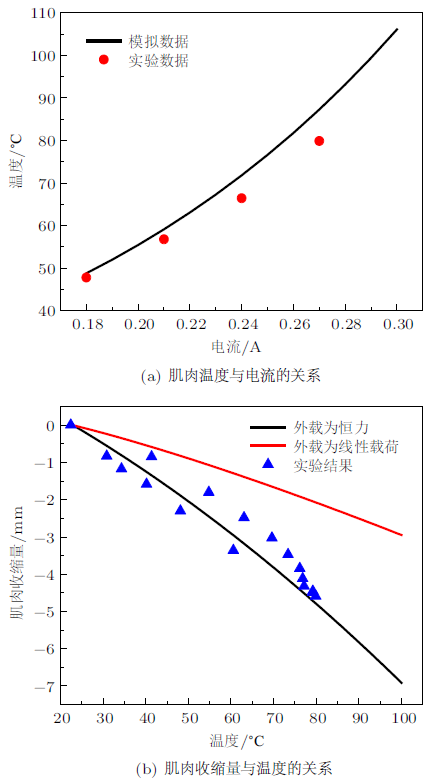
人工肌肉的温度与电流的关系如图5 (a)所示。分析表明,人工肌肉的温度随电流的增大呈抛物线型增加。当温度较低时,模拟结果与实验结果吻合;而当温度较高时,模拟结果与实验结果有差别。肌肉收缩量随温度的变化关系如图5 (b)所示。当外载为恒力时,肌肉收缩量随温度的升高线性增加,模拟结果与实验结果较为接近。当外载为弹簧提供的线性力时,肌肉收缩量同样随温度的升高线性增加。但是,同一温度下,后者相对前者的肌肉收缩量偏小。
图5
2.2 机械手指偏转的运动分析
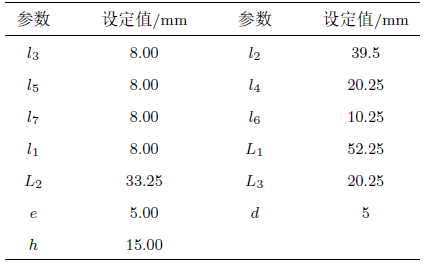
基于实际人类手指长度与关节比例,给出模拟机械手指偏转的结构参数,如表2 所示,对其偏转做运动分析。
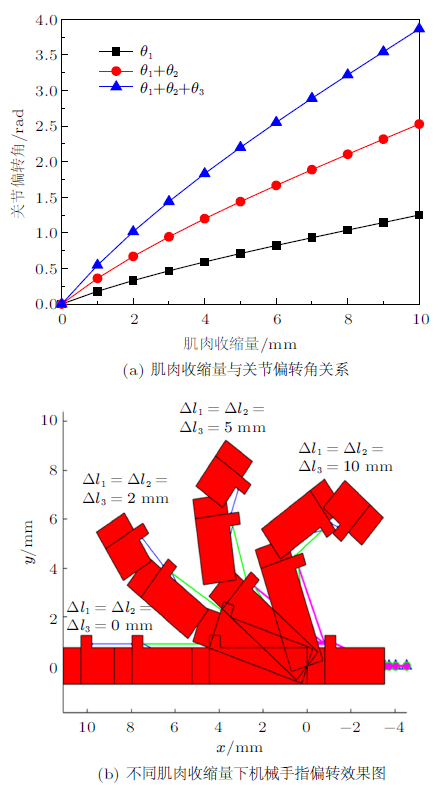
肌肉收缩量与各关节偏转角之间的关系如图6 (a)所示。分析表明,同一关节,其偏转角度随肌肉收缩量的增大而增大;同一肌肉收缩量,关节偏转角随关节尺寸的增大而减小。定义机械手指的驱动量转化比
(12) $\begin{eqnarray} \varDelta l_{{\rm rat}}=\frac{\varDelta l}{\theta }\end{eqnarray}$
式(12)描述了机械手指偏转过程中肌肉收缩量与关节偏转角之间的转化效果。由图6 (a)可知,各关节的驱动量转化比在0.1~0.25 rad/mm之间,且随着偏转角或肌肉收缩量的增大而减小。不同肌肉收缩量下机械手指各关节的偏转效果如图6 (b)所示。例如,当各肌肉收缩量达到5 mm时,手指已经发生了较大程度的偏转。
图6
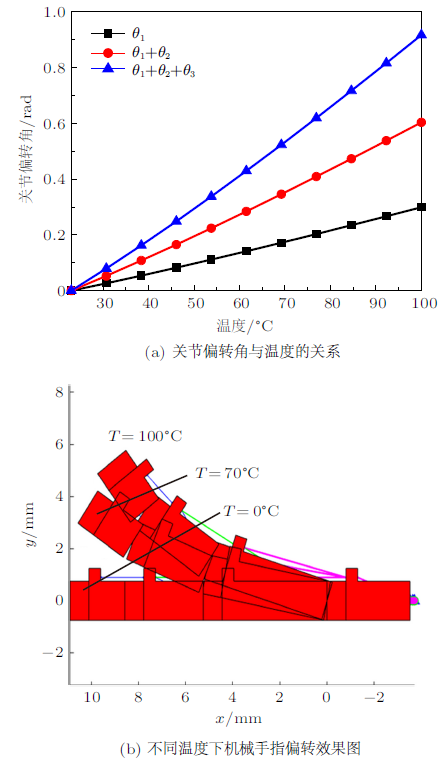
当机械手指采用人工肌肉驱动时,肌肉收缩量由温度和外载共同决定,因此,机械手指的关节偏转角最终取决于温度与外载。若外载为弹簧力时,对机械手指的偏转做运动分析。关节偏转角与温度的关系如图7 (a)所示。可见,关节偏转角随温度的升高而线性增大,但其增量并不明显。例如,当温度为100${^\circ}$C时,第一关节的偏转角为0.22 rad。不同温度下机械手指的偏转效果如图7 (b)所示。由图可知,随着温度的升高,关节偏转并不明显。结合图5 (b)与图6 (a)可知,当外载为弹簧力时,因肌肉收缩量相对较小,导致关节偏转角较小。
图7
3 结论
本文设计了一种采用螺旋卷绕型纤维基人工肌肉驱动的机械手指,改进了人工肌肉纤维热致动物理模型,建立了描述机械手指偏转运动的理论模型。主要结论包括:
(1)采用三股螺旋卷绕型纤维基人工肌肉驱动的机械手指,能够实现对各个关节偏转的独立控制,结合人工肌肉热致动物理模型,预测了各个关节的偏转角;
(2)在焦耳加热时,纤维基人工肌肉的温度随着电流的增大呈抛物线型增大,其致动量与肌肉温度线性正相关,且肌肉的致动效果依赖于其承受的外载形式;
(3)关节尺寸一定的情况下,其偏转角随着肌肉收缩量或温度的增加而增大,而驱动量转化比则相反;肌肉收缩量一定的情况下,关节偏转角随着关节尺寸的增大而减小。
参考文献
View Option
[1]
Mirvakili SM Hunter IW . Artificial muscles: mechanisms, applications, and challenges
Advanced Materials 2018 , 30 (6 ): 1704407
DOI
URL
[本文引用: 3]
[2]
Mirfakhrai T Madden JDW Baughman RH . Polymer artificial muscles
Materials Today 2007 , 10 (4 ): 30 -38
[本文引用: 1]
[3]
Spinks GM . Advanced actuator materials powered by biomimetic helical fiber topologies
Advanced Materials 2020 , 32 (18 ): 1904093
DOI
URL
[本文引用: 3]
[4]
Aziz S Spinks GM . Torsional artificial muscles
Materials Horizons 2020 , 7 (3 ): 667 -693
DOI
URL
[本文引用: 1]
[5]
张亚坤 , 张宇 , 李博 等 . 聚合物捻卷型人工肌肉及其在软体机器人领域应用的研究现状
中国科学: 技术科学 , 2021 , 51 (2 ): 119 -136
[本文引用: 1]
Zhang Yakun Zhang Yu Li Bo , et al . Progress of twisted and coiled polymer fiber artificial muscles and its application in soft robots
Sci Sin Tech 2021 , 51 (2 ): 119 -136 (in Chinese)
DOI
URL
[本文引用: 1]
[6]
Haines CS Lima MD Li N , et al . Artificial muscles from fishing line and sewing thread
Science 2014 , 343 (6173 ): 868 -872
DOI
URL
[本文引用: 1]
[7]
Yuan J Neri W Zakri C , et al . Shape memory nanocomposite fibers for untethered high-energy microengines
Science 2019 , 365 (6449 ): 155 -158
DOI
URL
[本文引用: 1]
[8]
张进华 , 王韬 , 洪军 等 . 软体机械手研究综述
机械工程学报 , 2017 , 53 (13 ): 19 -28
[本文引用: 1]
Zhang Jinhua Wang Tao Hong Jun , et al . Review of soft-bodied manipulator
Journal of Mechanical Engineering 2017 , 53 (13 ): 19 -28 (in Chinese)
[本文引用: 1]
[9]
Wu L de Andrade MJ Saharan LK , et al . Compact and low-cost humanoid hand powered by nylon artificial muscles
Bioinspiration and Biomimetics 2017 , 12 (2 ): 026004
DOI
URL
[本文引用: 4]
[10]
Tomovic R Boni G . An adaptive artificial hand
IRE Transactions on Automatic Control 1962 , 7 (3 ): 3 -10
[11]
Salisbury JK Craig JJ . Articulated hands: force control and kinematic issues
The International Journal of Robotics Research 1982 , 1 (1 ): 4 -17
DOI
URL
[12]
Jang G Lee C Lee H , et al . Robotic index finger prosthesis using stackable double 4-BAR mechanisms
Mechatronics 2013 , 23 (3 ): 318 -325
DOI
URL
[13]
Thayer N Priya S . Design and implementation of a dexterous anthropomorphic robotic typing (DART) hand
Smart Materials and Structures 2011 , 20 (3 ): 035010
DOI
URL
[本文引用: 1]
[14]
Arjun A Saharan L Tadesse Y . Design of a 3D printed hand prosthesis actuated by nylon 6-6 polymer based artificial muscles
2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX , 2016
[本文引用: 1]
[15]
Yip MC Niemeyer G . On the control and properties of supercoiled polymer artificial muscles
IEEE Transactions on Robotics 2017 , 33 (3 ): 689 -699
DOI
URL
[本文引用: 1]
[16]
Karami F Tadesse Y . Modeling of twisted and coiled polymer (TCP) muscle based on phenomenological approach
Smart Materials and Structures 2017 , 26 (12 ): 125010
DOI
URL
[本文引用: 5]
Artificial muscles: mechanisms, applications, and challenges
3
2018
... 自工业革命以来,人类发明了内燃机、电机、气动或液压等动力装置,这些装置对人类文明的发展起到了至关重要的作用.哺乳动物则利用肌肉纤维达到驱动效果.以骨骼肌为例,其输出应力约0.3 MPa,输出应变约20%,功率密度可达300 W/kg[1 ] .人工肌肉是指用于模仿天然肌肉的新材料或驱动装置,其可感受外部刺激(如光、电、热、湿度等)并在一个部件内收缩、膨胀或旋转,从而衍生出其他复杂类型的动作[2 -3 ] .如何模拟动物肌肉,进而制备出先进的人工肌肉纤维,是科学家最近研究的热点问题[1 ,3 -5 ] .2014年,Haines等[6 ] 利用聚合物纤维制作出的螺旋卷绕型纤维基人工肌肉(twisted and coiled polymer, TCP)具有如下的致动特性:当温度恒定时,肌肉相当于一个弹簧,外加载荷会导致肌肉的伸长;当温度升高时,肌肉会缩短.这种TCP人工肌肉一般由高性能纤维螺旋卷绕而成,其成本低、迟滞小、寿命长、变形量大、能量密度高,在柔性驱动技术领域具有广阔的应用前景[1 ,3 -4 ,7 ] . ...
... [1 ,3 -5 ].2014年,Haines等[6 ] 利用聚合物纤维制作出的螺旋卷绕型纤维基人工肌肉(twisted and coiled polymer, TCP)具有如下的致动特性:当温度恒定时,肌肉相当于一个弹簧,外加载荷会导致肌肉的伸长;当温度升高时,肌肉会缩短.这种TCP人工肌肉一般由高性能纤维螺旋卷绕而成,其成本低、迟滞小、寿命长、变形量大、能量密度高,在柔性驱动技术领域具有广阔的应用前景[1 ,3 -4 ,7 ] . ...
... [1 ,3 -4 ,7 ]. ...
Polymer artificial muscles
1
2007
... 自工业革命以来,人类发明了内燃机、电机、气动或液压等动力装置,这些装置对人类文明的发展起到了至关重要的作用.哺乳动物则利用肌肉纤维达到驱动效果.以骨骼肌为例,其输出应力约0.3 MPa,输出应变约20%,功率密度可达300 W/kg[1 ] .人工肌肉是指用于模仿天然肌肉的新材料或驱动装置,其可感受外部刺激(如光、电、热、湿度等)并在一个部件内收缩、膨胀或旋转,从而衍生出其他复杂类型的动作[2 -3 ] .如何模拟动物肌肉,进而制备出先进的人工肌肉纤维,是科学家最近研究的热点问题[1 ,3 -5 ] .2014年,Haines等[6 ] 利用聚合物纤维制作出的螺旋卷绕型纤维基人工肌肉(twisted and coiled polymer, TCP)具有如下的致动特性:当温度恒定时,肌肉相当于一个弹簧,外加载荷会导致肌肉的伸长;当温度升高时,肌肉会缩短.这种TCP人工肌肉一般由高性能纤维螺旋卷绕而成,其成本低、迟滞小、寿命长、变形量大、能量密度高,在柔性驱动技术领域具有广阔的应用前景[1 ,3 -4 ,7 ] . ...
Advanced actuator materials powered by biomimetic helical fiber topologies
3
2020
... 自工业革命以来,人类发明了内燃机、电机、气动或液压等动力装置,这些装置对人类文明的发展起到了至关重要的作用.哺乳动物则利用肌肉纤维达到驱动效果.以骨骼肌为例,其输出应力约0.3 MPa,输出应变约20%,功率密度可达300 W/kg[1 ] .人工肌肉是指用于模仿天然肌肉的新材料或驱动装置,其可感受外部刺激(如光、电、热、湿度等)并在一个部件内收缩、膨胀或旋转,从而衍生出其他复杂类型的动作[2 -3 ] .如何模拟动物肌肉,进而制备出先进的人工肌肉纤维,是科学家最近研究的热点问题[1 ,3 -5 ] .2014年,Haines等[6 ] 利用聚合物纤维制作出的螺旋卷绕型纤维基人工肌肉(twisted and coiled polymer, TCP)具有如下的致动特性:当温度恒定时,肌肉相当于一个弹簧,外加载荷会导致肌肉的伸长;当温度升高时,肌肉会缩短.这种TCP人工肌肉一般由高性能纤维螺旋卷绕而成,其成本低、迟滞小、寿命长、变形量大、能量密度高,在柔性驱动技术领域具有广阔的应用前景[1 ,3 -4 ,7 ] . ...
... ,3 -5 ].2014年,Haines等[6 ] 利用聚合物纤维制作出的螺旋卷绕型纤维基人工肌肉(twisted and coiled polymer, TCP)具有如下的致动特性:当温度恒定时,肌肉相当于一个弹簧,外加载荷会导致肌肉的伸长;当温度升高时,肌肉会缩短.这种TCP人工肌肉一般由高性能纤维螺旋卷绕而成,其成本低、迟滞小、寿命长、变形量大、能量密度高,在柔性驱动技术领域具有广阔的应用前景[1 ,3 -4 ,7 ] . ...
... ,3 -4 ,7 ]. ...
Torsional artificial muscles
1
2020
... 自工业革命以来,人类发明了内燃机、电机、气动或液压等动力装置,这些装置对人类文明的发展起到了至关重要的作用.哺乳动物则利用肌肉纤维达到驱动效果.以骨骼肌为例,其输出应力约0.3 MPa,输出应变约20%,功率密度可达300 W/kg[1 ] .人工肌肉是指用于模仿天然肌肉的新材料或驱动装置,其可感受外部刺激(如光、电、热、湿度等)并在一个部件内收缩、膨胀或旋转,从而衍生出其他复杂类型的动作[2 -3 ] .如何模拟动物肌肉,进而制备出先进的人工肌肉纤维,是科学家最近研究的热点问题[1 ,3 -5 ] .2014年,Haines等[6 ] 利用聚合物纤维制作出的螺旋卷绕型纤维基人工肌肉(twisted and coiled polymer, TCP)具有如下的致动特性:当温度恒定时,肌肉相当于一个弹簧,外加载荷会导致肌肉的伸长;当温度升高时,肌肉会缩短.这种TCP人工肌肉一般由高性能纤维螺旋卷绕而成,其成本低、迟滞小、寿命长、变形量大、能量密度高,在柔性驱动技术领域具有广阔的应用前景[1 ,3 -4 ,7 ] . ...
聚合物捻卷型人工肌肉及其在软体机器人领域应用的研究现状
1
2021
... 自工业革命以来,人类发明了内燃机、电机、气动或液压等动力装置,这些装置对人类文明的发展起到了至关重要的作用.哺乳动物则利用肌肉纤维达到驱动效果.以骨骼肌为例,其输出应力约0.3 MPa,输出应变约20%,功率密度可达300 W/kg[1 ] .人工肌肉是指用于模仿天然肌肉的新材料或驱动装置,其可感受外部刺激(如光、电、热、湿度等)并在一个部件内收缩、膨胀或旋转,从而衍生出其他复杂类型的动作[2 -3 ] .如何模拟动物肌肉,进而制备出先进的人工肌肉纤维,是科学家最近研究的热点问题[1 ,3 -5 ] .2014年,Haines等[6 ] 利用聚合物纤维制作出的螺旋卷绕型纤维基人工肌肉(twisted and coiled polymer, TCP)具有如下的致动特性:当温度恒定时,肌肉相当于一个弹簧,外加载荷会导致肌肉的伸长;当温度升高时,肌肉会缩短.这种TCP人工肌肉一般由高性能纤维螺旋卷绕而成,其成本低、迟滞小、寿命长、变形量大、能量密度高,在柔性驱动技术领域具有广阔的应用前景[1 ,3 -4 ,7 ] . ...
聚合物捻卷型人工肌肉及其在软体机器人领域应用的研究现状
1
2021
... 自工业革命以来,人类发明了内燃机、电机、气动或液压等动力装置,这些装置对人类文明的发展起到了至关重要的作用.哺乳动物则利用肌肉纤维达到驱动效果.以骨骼肌为例,其输出应力约0.3 MPa,输出应变约20%,功率密度可达300 W/kg[1 ] .人工肌肉是指用于模仿天然肌肉的新材料或驱动装置,其可感受外部刺激(如光、电、热、湿度等)并在一个部件内收缩、膨胀或旋转,从而衍生出其他复杂类型的动作[2 -3 ] .如何模拟动物肌肉,进而制备出先进的人工肌肉纤维,是科学家最近研究的热点问题[1 ,3 -5 ] .2014年,Haines等[6 ] 利用聚合物纤维制作出的螺旋卷绕型纤维基人工肌肉(twisted and coiled polymer, TCP)具有如下的致动特性:当温度恒定时,肌肉相当于一个弹簧,外加载荷会导致肌肉的伸长;当温度升高时,肌肉会缩短.这种TCP人工肌肉一般由高性能纤维螺旋卷绕而成,其成本低、迟滞小、寿命长、变形量大、能量密度高,在柔性驱动技术领域具有广阔的应用前景[1 ,3 -4 ,7 ] . ...
Artificial muscles from fishing line and sewing thread
1
2014
... 自工业革命以来,人类发明了内燃机、电机、气动或液压等动力装置,这些装置对人类文明的发展起到了至关重要的作用.哺乳动物则利用肌肉纤维达到驱动效果.以骨骼肌为例,其输出应力约0.3 MPa,输出应变约20%,功率密度可达300 W/kg[1 ] .人工肌肉是指用于模仿天然肌肉的新材料或驱动装置,其可感受外部刺激(如光、电、热、湿度等)并在一个部件内收缩、膨胀或旋转,从而衍生出其他复杂类型的动作[2 -3 ] .如何模拟动物肌肉,进而制备出先进的人工肌肉纤维,是科学家最近研究的热点问题[1 ,3 -5 ] .2014年,Haines等[6 ] 利用聚合物纤维制作出的螺旋卷绕型纤维基人工肌肉(twisted and coiled polymer, TCP)具有如下的致动特性:当温度恒定时,肌肉相当于一个弹簧,外加载荷会导致肌肉的伸长;当温度升高时,肌肉会缩短.这种TCP人工肌肉一般由高性能纤维螺旋卷绕而成,其成本低、迟滞小、寿命长、变形量大、能量密度高,在柔性驱动技术领域具有广阔的应用前景[1 ,3 -4 ,7 ] . ...
Shape memory nanocomposite fibers for untethered high-energy microengines
1
2019
... 自工业革命以来,人类发明了内燃机、电机、气动或液压等动力装置,这些装置对人类文明的发展起到了至关重要的作用.哺乳动物则利用肌肉纤维达到驱动效果.以骨骼肌为例,其输出应力约0.3 MPa,输出应变约20%,功率密度可达300 W/kg[1 ] .人工肌肉是指用于模仿天然肌肉的新材料或驱动装置,其可感受外部刺激(如光、电、热、湿度等)并在一个部件内收缩、膨胀或旋转,从而衍生出其他复杂类型的动作[2 -3 ] .如何模拟动物肌肉,进而制备出先进的人工肌肉纤维,是科学家最近研究的热点问题[1 ,3 -5 ] .2014年,Haines等[6 ] 利用聚合物纤维制作出的螺旋卷绕型纤维基人工肌肉(twisted and coiled polymer, TCP)具有如下的致动特性:当温度恒定时,肌肉相当于一个弹簧,外加载荷会导致肌肉的伸长;当温度升高时,肌肉会缩短.这种TCP人工肌肉一般由高性能纤维螺旋卷绕而成,其成本低、迟滞小、寿命长、变形量大、能量密度高,在柔性驱动技术领域具有广阔的应用前景[1 ,3 -4 ,7 ] . ...
软体机械手研究综述
1
2017
... 人手能够完成各种复杂的操作,但机械末端结构机械手完成这些动作并非易事.模仿人手来研究具有多关节的多指机械手的物体抓取、把持等日常动作有着重要的意义.机械手指的设计和制造核心包括执行器材料的选取、驱动方式的选择、手指驱动模型的建立等[8 -9 ] .近年来,随着各种驱动、传感和控制技术的进步,多自由度机械手的研究也取得了较大的发展[9 -13 ] ,能够抓取各种物体.传统的机械手指多采用直流电动机、气动或液压驱动器,这些常规驱动器一般比较笨重或昂贵.目前研究人员已开始尝试采用纤维基人工肌肉驱动器、形状记忆合金等低轮廓驱动器.2016年,Arjun等[14 ] 设计了一种采用TCP人工肌肉驱动的假肢手.2017年,Wu等[9 ] 提出了一种以TCP人工肌肉为驱动的新型手指模型,通过对人工肌肉的热驱动实现手指两侧的任意偏转.他们研究了三个关节的相对偏转角$\theta_{1}$,$\theta_{2}$,$\theta_{3}$和肌肉收缩量之间的关系.随后关于这种手指实物模型的研究,大多采用Wu等[9 ] 的理论模型.但是,该模型存在的问题是模型两侧都仅采用一股人工肌肉驱动,即多个关节的偏转只对应于一个收缩量,因此,无法控制各个关节的独立转动.随后,Yip等[15 ] 在纤维基人工肌肉力与位置控制系统的基础上,通过多根人工肌肉的组合驱动,实现了仿生机械手的多指弯曲动作和手臂摆动动作. ...
软体机械手研究综述
1
2017
... 人手能够完成各种复杂的操作,但机械末端结构机械手完成这些动作并非易事.模仿人手来研究具有多关节的多指机械手的物体抓取、把持等日常动作有着重要的意义.机械手指的设计和制造核心包括执行器材料的选取、驱动方式的选择、手指驱动模型的建立等[8 -9 ] .近年来,随着各种驱动、传感和控制技术的进步,多自由度机械手的研究也取得了较大的发展[9 -13 ] ,能够抓取各种物体.传统的机械手指多采用直流电动机、气动或液压驱动器,这些常规驱动器一般比较笨重或昂贵.目前研究人员已开始尝试采用纤维基人工肌肉驱动器、形状记忆合金等低轮廓驱动器.2016年,Arjun等[14 ] 设计了一种采用TCP人工肌肉驱动的假肢手.2017年,Wu等[9 ] 提出了一种以TCP人工肌肉为驱动的新型手指模型,通过对人工肌肉的热驱动实现手指两侧的任意偏转.他们研究了三个关节的相对偏转角$\theta_{1}$,$\theta_{2}$,$\theta_{3}$和肌肉收缩量之间的关系.随后关于这种手指实物模型的研究,大多采用Wu等[9 ] 的理论模型.但是,该模型存在的问题是模型两侧都仅采用一股人工肌肉驱动,即多个关节的偏转只对应于一个收缩量,因此,无法控制各个关节的独立转动.随后,Yip等[15 ] 在纤维基人工肌肉力与位置控制系统的基础上,通过多根人工肌肉的组合驱动,实现了仿生机械手的多指弯曲动作和手臂摆动动作. ...
Compact and low-cost humanoid hand powered by nylon artificial muscles
4
2017
... 人手能够完成各种复杂的操作,但机械末端结构机械手完成这些动作并非易事.模仿人手来研究具有多关节的多指机械手的物体抓取、把持等日常动作有着重要的意义.机械手指的设计和制造核心包括执行器材料的选取、驱动方式的选择、手指驱动模型的建立等[8 -9 ] .近年来,随着各种驱动、传感和控制技术的进步,多自由度机械手的研究也取得了较大的发展[9 -13 ] ,能够抓取各种物体.传统的机械手指多采用直流电动机、气动或液压驱动器,这些常规驱动器一般比较笨重或昂贵.目前研究人员已开始尝试采用纤维基人工肌肉驱动器、形状记忆合金等低轮廓驱动器.2016年,Arjun等[14 ] 设计了一种采用TCP人工肌肉驱动的假肢手.2017年,Wu等[9 ] 提出了一种以TCP人工肌肉为驱动的新型手指模型,通过对人工肌肉的热驱动实现手指两侧的任意偏转.他们研究了三个关节的相对偏转角$\theta_{1}$,$\theta_{2}$,$\theta_{3}$和肌肉收缩量之间的关系.随后关于这种手指实物模型的研究,大多采用Wu等[9 ] 的理论模型.但是,该模型存在的问题是模型两侧都仅采用一股人工肌肉驱动,即多个关节的偏转只对应于一个收缩量,因此,无法控制各个关节的独立转动.随后,Yip等[15 ] 在纤维基人工肌肉力与位置控制系统的基础上,通过多根人工肌肉的组合驱动,实现了仿生机械手的多指弯曲动作和手臂摆动动作. ...
... [9 -13 ],能够抓取各种物体.传统的机械手指多采用直流电动机、气动或液压驱动器,这些常规驱动器一般比较笨重或昂贵.目前研究人员已开始尝试采用纤维基人工肌肉驱动器、形状记忆合金等低轮廓驱动器.2016年,Arjun等[14 ] 设计了一种采用TCP人工肌肉驱动的假肢手.2017年,Wu等[9 ] 提出了一种以TCP人工肌肉为驱动的新型手指模型,通过对人工肌肉的热驱动实现手指两侧的任意偏转.他们研究了三个关节的相对偏转角$\theta_{1}$,$\theta_{2}$,$\theta_{3}$和肌肉收缩量之间的关系.随后关于这种手指实物模型的研究,大多采用Wu等[9 ] 的理论模型.但是,该模型存在的问题是模型两侧都仅采用一股人工肌肉驱动,即多个关节的偏转只对应于一个收缩量,因此,无法控制各个关节的独立转动.随后,Yip等[15 ] 在纤维基人工肌肉力与位置控制系统的基础上,通过多根人工肌肉的组合驱动,实现了仿生机械手的多指弯曲动作和手臂摆动动作. ...
... [9 ]提出了一种以TCP人工肌肉为驱动的新型手指模型,通过对人工肌肉的热驱动实现手指两侧的任意偏转.他们研究了三个关节的相对偏转角$\theta_{1}$,$\theta_{2}$,$\theta_{3}$和肌肉收缩量之间的关系.随后关于这种手指实物模型的研究,大多采用Wu等[9 ] 的理论模型.但是,该模型存在的问题是模型两侧都仅采用一股人工肌肉驱动,即多个关节的偏转只对应于一个收缩量,因此,无法控制各个关节的独立转动.随后,Yip等[15 ] 在纤维基人工肌肉力与位置控制系统的基础上,通过多根人工肌肉的组合驱动,实现了仿生机械手的多指弯曲动作和手臂摆动动作. ...
... [9 ]的理论模型.但是,该模型存在的问题是模型两侧都仅采用一股人工肌肉驱动,即多个关节的偏转只对应于一个收缩量,因此,无法控制各个关节的独立转动.随后,Yip等[15 ] 在纤维基人工肌肉力与位置控制系统的基础上,通过多根人工肌肉的组合驱动,实现了仿生机械手的多指弯曲动作和手臂摆动动作. ...
An adaptive artificial hand
0
1962
Articulated hands: force control and kinematic issues
0
1982
Robotic index finger prosthesis using stackable double 4-BAR mechanisms
0
2013
Design and implementation of a dexterous anthropomorphic robotic typing (DART) hand
1
2011
... 人手能够完成各种复杂的操作,但机械末端结构机械手完成这些动作并非易事.模仿人手来研究具有多关节的多指机械手的物体抓取、把持等日常动作有着重要的意义.机械手指的设计和制造核心包括执行器材料的选取、驱动方式的选择、手指驱动模型的建立等[8 -9 ] .近年来,随着各种驱动、传感和控制技术的进步,多自由度机械手的研究也取得了较大的发展[9 -13 ] ,能够抓取各种物体.传统的机械手指多采用直流电动机、气动或液压驱动器,这些常规驱动器一般比较笨重或昂贵.目前研究人员已开始尝试采用纤维基人工肌肉驱动器、形状记忆合金等低轮廓驱动器.2016年,Arjun等[14 ] 设计了一种采用TCP人工肌肉驱动的假肢手.2017年,Wu等[9 ] 提出了一种以TCP人工肌肉为驱动的新型手指模型,通过对人工肌肉的热驱动实现手指两侧的任意偏转.他们研究了三个关节的相对偏转角$\theta_{1}$,$\theta_{2}$,$\theta_{3}$和肌肉收缩量之间的关系.随后关于这种手指实物模型的研究,大多采用Wu等[9 ] 的理论模型.但是,该模型存在的问题是模型两侧都仅采用一股人工肌肉驱动,即多个关节的偏转只对应于一个收缩量,因此,无法控制各个关节的独立转动.随后,Yip等[15 ] 在纤维基人工肌肉力与位置控制系统的基础上,通过多根人工肌肉的组合驱动,实现了仿生机械手的多指弯曲动作和手臂摆动动作. ...
Design of a 3D printed hand prosthesis actuated by nylon 6-6 polymer based artificial muscles
1
2016
... 人手能够完成各种复杂的操作,但机械末端结构机械手完成这些动作并非易事.模仿人手来研究具有多关节的多指机械手的物体抓取、把持等日常动作有着重要的意义.机械手指的设计和制造核心包括执行器材料的选取、驱动方式的选择、手指驱动模型的建立等[8 -9 ] .近年来,随着各种驱动、传感和控制技术的进步,多自由度机械手的研究也取得了较大的发展[9 -13 ] ,能够抓取各种物体.传统的机械手指多采用直流电动机、气动或液压驱动器,这些常规驱动器一般比较笨重或昂贵.目前研究人员已开始尝试采用纤维基人工肌肉驱动器、形状记忆合金等低轮廓驱动器.2016年,Arjun等[14 ] 设计了一种采用TCP人工肌肉驱动的假肢手.2017年,Wu等[9 ] 提出了一种以TCP人工肌肉为驱动的新型手指模型,通过对人工肌肉的热驱动实现手指两侧的任意偏转.他们研究了三个关节的相对偏转角$\theta_{1}$,$\theta_{2}$,$\theta_{3}$和肌肉收缩量之间的关系.随后关于这种手指实物模型的研究,大多采用Wu等[9 ] 的理论模型.但是,该模型存在的问题是模型两侧都仅采用一股人工肌肉驱动,即多个关节的偏转只对应于一个收缩量,因此,无法控制各个关节的独立转动.随后,Yip等[15 ] 在纤维基人工肌肉力与位置控制系统的基础上,通过多根人工肌肉的组合驱动,实现了仿生机械手的多指弯曲动作和手臂摆动动作. ...
On the control and properties of supercoiled polymer artificial muscles
1
2017
... 人手能够完成各种复杂的操作,但机械末端结构机械手完成这些动作并非易事.模仿人手来研究具有多关节的多指机械手的物体抓取、把持等日常动作有着重要的意义.机械手指的设计和制造核心包括执行器材料的选取、驱动方式的选择、手指驱动模型的建立等[8 -9 ] .近年来,随着各种驱动、传感和控制技术的进步,多自由度机械手的研究也取得了较大的发展[9 -13 ] ,能够抓取各种物体.传统的机械手指多采用直流电动机、气动或液压驱动器,这些常规驱动器一般比较笨重或昂贵.目前研究人员已开始尝试采用纤维基人工肌肉驱动器、形状记忆合金等低轮廓驱动器.2016年,Arjun等[14 ] 设计了一种采用TCP人工肌肉驱动的假肢手.2017年,Wu等[9 ] 提出了一种以TCP人工肌肉为驱动的新型手指模型,通过对人工肌肉的热驱动实现手指两侧的任意偏转.他们研究了三个关节的相对偏转角$\theta_{1}$,$\theta_{2}$,$\theta_{3}$和肌肉收缩量之间的关系.随后关于这种手指实物模型的研究,大多采用Wu等[9 ] 的理论模型.但是,该模型存在的问题是模型两侧都仅采用一股人工肌肉驱动,即多个关节的偏转只对应于一个收缩量,因此,无法控制各个关节的独立转动.随后,Yip等[15 ] 在纤维基人工肌肉力与位置控制系统的基础上,通过多根人工肌肉的组合驱动,实现了仿生机械手的多指弯曲动作和手臂摆动动作. ...
Modeling of twisted and coiled polymer (TCP) muscle based on phenomenological approach
5
2017
... 本文旨在提出一种由TCP人工肌肉驱动的灵巧、紧凑、低成本的机械手指新模型,实现机械手指在三个自由度上的独立驱动,使其更加符合人类手指的运动学规律.同时,基于Karami等[16 ] 的热驱动物理模型,通过数值模拟对所制备的纤维基人工肌肉的热致动效果以及手指模型的偏转效果进行预测,证明纤维基人工肌肉在仿生机械手应用中的有效性. ...
... 针对热驱动螺旋卷绕型纤维基人工肌肉,本文采用Karami等[16 ] 提出的物理模型.如图4 所示,单股人工肌肉表面缠绕铜丝,肌肉初始受拉伸,当$t=0$时,在铜丝中通入电流使肌肉升温,$t$时刻肌肉温度变为[16 ] ...
... [16 ] ...
... 基于对文献[16 ]中实验数据的分析,给出用于模拟温度变化时肌肉收缩量的材料参数,如表1 所示.采用这些材料、结构和环境参数,对温度变化时肌肉的收缩量进行分析. ...
... 注:标有*号的量采用文献[16 ]实验数据的修正值. ...