为了提高教学质量,近年来在教育部持续推动下,一流课程(金课)建设成为全国高校教育教学改革的重点工作。作为一流课程的主要特征, “两性一度”(高阶性、创新性与挑战度)已经广泛出现在各级各类教学要求与制度中,其核心在于利用“创新性”的方法,通过具有“挑战 度”的训练,达到培养“高阶性”思维的目的。
相比以记忆、理解与应用为特征的低阶思维模式,高阶思维模式(分析/评价/创造)体现在对问题的认知经历“盲目相信/众说纷纭/批判思 维”的过程,最终建立基于自身理解的、对客观事物全面与深刻的认识。达成该目标的关键在于教学内容的设计—通过具有挑战性问题的教学内容与环节,引导学生全面思考与深入探究,逐步形成批判性思维模式。
对于理工科专业课程,尽管不同课程在性质与内容上不尽相同,但总体而言,通过以下方面引入问题与思考是有益的:
为了不偏离课程主体内容,并且考虑到受众比例,挑战性问题的课程内容设计需要满足:起点低、台阶小、空间大,在这一点上,非常类似于各类电子游戏的设计。为了说明以上思路,本文以材料力学课程教学的一个实例展示问题引导与启发过程。
1 原始问题与标准解答
课程内容设计的出发点最好基于教科书的题目与叙述,这就是所谓的起点足够“低”。
在材料力学或弹性力学有关功(位移)的互等定理部分有如下或类似的习题[1 -2 ] :
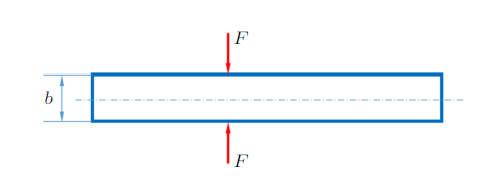
图1 所示等截面直杆,承受一对方向相反、大小均为$F$的横向集中力作用。设截面横向尺寸为$b$、拉压刚度为$EA$,材料的泊松比为$\mu $。试利用功的互等定理,证明杆的轴向变形为$\Delta l={\mu bF}/({EA})$。
图1
该题目简单而典型,也常常被教师选择作为例题讲解,教科书给出的标准解答如下。
对于该杆件构造另一种载荷状态如图2 所示,在杆件上施加一对大小相等,方向相反的轴向力$F_{1}$。
图2
(1) $\begin{eqnarray} \label{eq1} \Delta b=-\mu \varepsilon b=-\frac{\mu F_{1} b}{EA} \end{eqnarray}$
(2) $\begin{eqnarray} \label{eq2} F_{1} \cdot \Delta l=-F\cdot \left( {-\frac{\mu F_{1} b}{EA}} \right) \end{eqnarray}$
(3) $\begin{eqnarray} \label{eq3} \Delta l=\frac{\mu bF}{EA} \end{eqnarray}$
2 提出疑惑与概念辨析
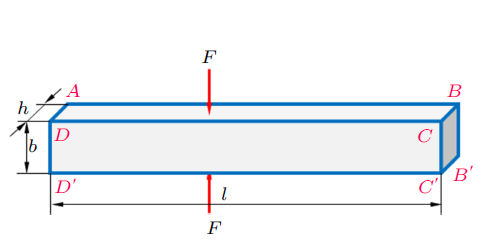
除了教科书给出的标准解答,这里展示另一种模式的证明。首先,为了方便后续讲解与符号说明,把图1 中结构画为三维模式,见图3 ,载荷$F$作用面的横向尺寸为$h$,轴向长度为$l$。
图3
(4) $\begin{eqnarray} \label{eq4} \varepsilon_{b} =\frac{\sigma }{E}=-\frac{F}{Ehl} \end{eqnarray}$
(5) $\begin{eqnarray} \label{eq5} \varepsilon_{l} =-\mu \varepsilon_{b} =\frac{\mu F}{Ehl} \end{eqnarray}$
(6) $\begin{eqnarray} \label{eq6} \Delta l=\varepsilon_{l} l=\frac{\mu F}{Eh}=\frac{\mu bF}{EA} \end{eqnarray}$
该证明模式并不完全由教师“制造”,由于此例为教科书上作业题,笔者多年统计数据,发现有25%以上的学生给出了第二种模式的证明过程。
事实上,引发学生思考的出发点从学生作业错误或者学生日常问题入手是最为合适的,因为其符合学生思考问题的思维模式。
该证明的错误之处在于:面$ABCD$上横向载荷$F$为集中力,在长度$l$范围内无论横向应力或应变都是非均匀分布,式(4)所得横向应变 表达式在全局范围内不正确。
该证明“找错”的过程,对于辨析概念与对象,例如应力与平均应力,集中力与分布力,微元体与分离体等方面,教师引导学生进行问题讨论是有益的。
3 扩展研究与理解进阶
尽管上面给出的证明模式是错误的,但是根据式(4)$\sim$式(6)给出的最终结果与正确答案却完全一致,由此可以提出的下一个问题是:答案一致是一种“巧合”还是有其“必然”?
这个问题可以随着上面讨论与讲解一次性提出,但是学生立刻就能给出比较全面的解答是不现实的,可以作为思考题布置并在下一次作为专题研讨。为了在学生讨论时引导重点与主线,教师完成相关课程内容设计作为预案是有益的,以下问题的分析展示了逐步提升思 维训练的过程。
3.1 载荷从均匀分布到集中作用
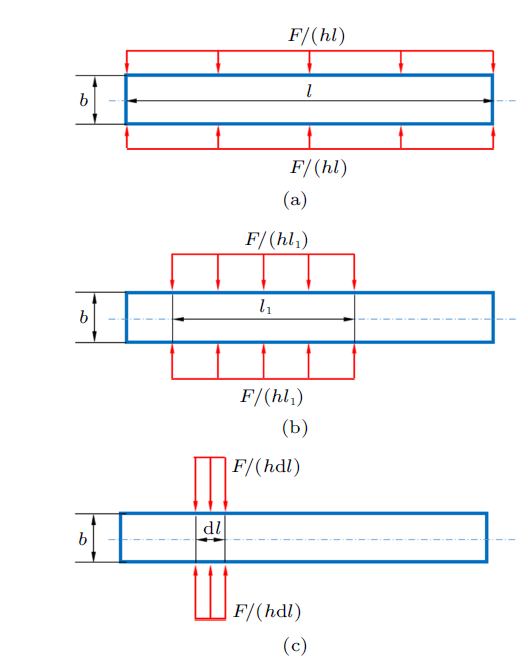
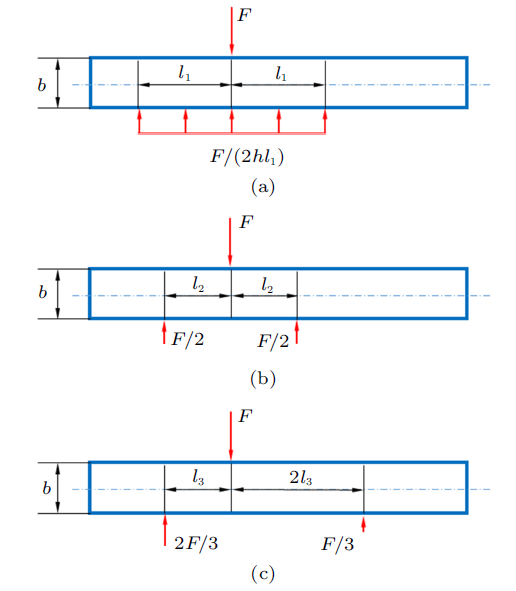
首先,尽管式(4)$\sim$式(6)的证明过程对于原题是错误的,但对于作用于$ABCD$与$A'B'C'D'$的横向均布面载$F/(hl)$而言(见图4 (a),为 了文本简洁,受力图均为正视图,下同),该证明过程是正确的。
图4
其次,当均布载荷在轴向的作用范围仅为$ABCD$的一个局部,例如$l_{1}$ ($l_{1}<l$),且分布载荷大小为$F/(hl_{1})$ (总载荷一致,见图4 (b))。则在$l_{1}$范围内与图4 (a)的情况完全一致,其他范围没有轴向变形,总的轴向变形$\Delta l$仍为
(7) $\begin{eqnarray} \label{eq7} \Delta l=\varepsilon_{l_{1} } l_{1} =\frac{\mu Fl_{1} }{Ehl_{1} }=\frac{\mu bF}{EA} \end{eqnarray}$
最终,上述模式的极端情况,当$l_{1} \to {\rm d}l$(图4 (c)),
(8) $\begin{eqnarray} \label{eq8} \lim\limits_{{\rm d}l\to 0} \Delta l=\lim\limits_{{\rm d}l\to 0} \varepsilon_{{\rm d}l} {\rm d}l=\lim\limits_{{\rm d}l\to 0} \frac{\mu F{\rm d}l}{Eh{\rm d}l}=\frac{\mu bF}{EA} \end{eqnarray}$
以上的证明过程是基于均匀应变以及极限化模式,同样可以采用构造如图2 的轴向载荷状态,利用功的互等定理得到同样结果,此处不再赘述。
从该变化过程可以看出,无论载荷分布形式与位置如何,对于静力等效的一对横向作用力,其在轴向引入的变形均为同一数值,所以第二节中尽管证明过程是错误的,但是答案完全一致有其必然性。
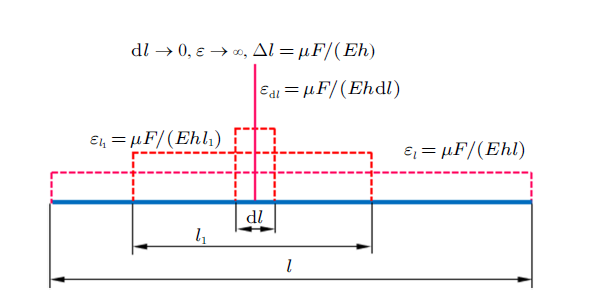
事实上,我们可以把以上的证明与分析结果画在一张图上(如图5 ):随着载荷集度的增加,在载荷作用范围内,轴向变形的集度也线性增加,但总变形(对应于虚线包围的面积)保持不变,极限状态为载荷分布范围趋于零,此时变形集度趋于无穷大,但二者乘 积(总变形量)为一有限值并保持不变。
图5
以上分析过程中有多个“台阶”,每次上升的幅度不大,而且相互关系紧密,最后的总结已经在数学本质上有所体现。
3.2 载荷分布从局部平衡到总体平衡
观察图4 中各种载荷分布状态,尽管轴向分布区域不同,但横向均为对称模式,即任意局部尺度上载荷都是平衡的;如果载荷只是总体平衡而非各局部均平衡,如图6 所示各种状况,轴向总变形会发生变化吗?
图6
解决这类载荷分布状况比较简单的方式是采用叠加方法:
(1)当上下表面载荷互换时,所产生的轴向变形完全相同,所以这两种载荷叠加后获得的轴向变形为单独载荷状况的2倍;
(2)叠加后的载荷可以重新分解为与图4 类似的横向对称模式的组合,可以采用上节中的计算方法得到完全一致的结果。
可能这种处理方式不是唯一的,但以此为基础引导学生讨论是有趣的。
相比上节限定于原始问题,学生主动想到这类载荷分布状况的可能性较小,但对该问题处理的方式体现了利用已有知识与方法解决新问题的灵活性。
3.3 载荷分布方式引入的位移量级对比
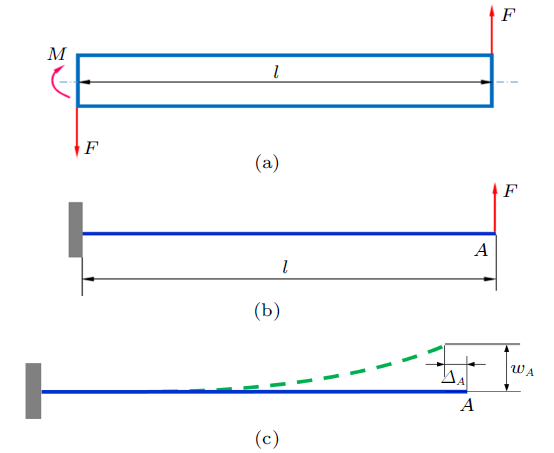
与3.1节不同,在3.2节中载荷分布模式不仅导致轴向变形,而且伴随着横向弯曲变形,其一种分布模式的极端化状态如图7 (a),相当于悬臂 梁自由端承受集中载荷如图7 (b) (受力简图)。对于该受力状态导致的轴线变形$\Delta l$仍然可以使用3.2节的计算方法,但是需要注意,由于弯曲变形的影响,轴线由直线变为曲线,在水平$x$方向(原始轴线方向)自由端也有水平方向位移$\Delta _{A} $。
图7
水平方向位移$\varDelta_{A}$ (如图7 (c))也称为曲率缩短,通过挠曲轴总长与其水平轴投影之差进行计算[3 ] ,通用计算公式是泰勒展开的近似表达
(9) $\begin{eqnarray} \label{eq9} \varDelta_{A} \approx \frac{1}{2}\int_l {\left( {{w}'} \right)^{2}} {\rm d}x \end{eqnarray}$
材料力学中梁弯曲变形的分析基于纯弯曲率公式,忽略了剪切影响并在小变形条件下进一步简化获得挠曲轴方程。经典教材中均提及忽略梁轴线方向的位移[1 ,4 -6 ] (横力弯曲条件下包括曲率缩短与轴线变形),但一般都没有给出各量量级的讨论,此处比较图7 中梁的自由端挠度$w_{A}$,自由端水平位移$\varDelta_{A} $,以及梁轴线长度变化$\Delta l$的量级,对于理解基本概念是有益的(为了符合梁弯曲的图注习惯,下列公式中载荷作用方向的截面横向尺寸改为$h$)
(10a) $\begin{eqnarray} && w_{A} =\frac{Fl^{3}}{3EI}\end{eqnarray}$
(10b) $\begin{eqnarray} && \varDelta_{A} \approx \frac{F^{2}l^{5}}{15E^{2}I^{2}},\mbox{ }\frac{\varDelta_{A} }{w_{A} }=\frac{3}{5}\frac{w_{A} }{l}\end{eqnarray}$
(10c) $\begin{eqnarray} && \Delta l=\frac{\mu Fh}{EA},\mbox{ }\frac{\Delta l}{w_{A} }=\frac{\mu h^{3}}{4l^{3}} \end{eqnarray}$
在小变形条件下,各变形(位移)量相对于梁长度均为小量,挠度$w_{A}$是学生们非常熟悉的量,根据式(10b)与式(10c)中与$w_{A}$的比较,水 平位移$\varDelta_{A} $与轴线长度变化$\Delta l$均为挠度$w_{A}$的小量,相对而言
(11a) $\begin{eqnarray} \frac{\varDelta_{A} }{\Delta l}=\frac{Fl^{5}b}{15\mu EI^{2}}=\frac{144}{15\mu }\frac{F}{EA}\left( {\frac{l}{h}} \right)^{5} \end{eqnarray}$
使用弯曲应变$\varepsilon_{M} $代入式(11a)
(11b) $\begin{eqnarray} \frac{\varDelta_{A} }{\Delta l}=\frac{144}{90\mu }\varepsilon_{M} \left( {\frac{l}{h}} \right)^{4} \end{eqnarray}$
以常见弯曲应变范围$\varepsilon_{M} =1.0^{-4}\sim1.0^{-3}$代入式(11b)评估比值,对于工程长梁,一般情况下$\varDelta_{A} $至少比$\Delta l$大一个量级。
梁的横向位移有非常明显的长度放大效应,与挠度$w_{A} $和水平位移$\varDelta_{A}$不同,轴线长度变化$\Delta l$与梁的长度无关,这是其相对较小的主要原因。
该部分的讨论关联了课程内容中的不同章节,而且需要资料查阅与相关数学推导,体现了思维训练的深度与广度,展示了课程内容设计的“空间大”。
4 小结
知识结构与能力培养是专业培养目标的核心表述,课程教学的目的最终体现在支持学生学习并达成能力培养。在高阶性思维能力的训练环节中,教师主导的课程内容设计是难点:
(1) 问题的引入不能完全脱离教材内容,须适合大部分学生水平,从教材内容、例题与习题出发是最佳途径;
(2) 能够通过简单分析运算获得明确结论的问题比较好,工程实际问题影响参数较多且分析过程过于复杂更适合课程背景介绍,不宜 作为课堂教学深入研讨的内容;
(3) 问题的讨论可以在不同层次展开并关联教材多个章节,便于学生进行概念辨析和知识体系构筑。
为了说明主体思路,本文从一个学生作业与问题出发,展示了批判性思维训练引导过程,希望对于相关课程内容设计有一定参考价值。
参考文献
View Option
[1]
单辉祖 . 材料力学, 第3版 . 北京 : 高等教育出版社 , 2010
[本文引用: 2]
[2]
Timoshenko SP Goodier JN . Theory of Elasticity, 3rd edn
New York: McGraw-Hill Education , 2013
[本文引用: 1]
[3]
单辉祖 . 材料力学问题、例题与分析方法 . 北京 : 高等教育出版社 , 2006
[本文引用: 1]
[4]
孙训方 等 材料力学, 第5版 . 北京 : 高等教育出版社 , 2009
[本文引用: 1]
[5]
刘鸿文 材料力学, 第5版 . 北京 : 高等教育出版社 , 2011
[6]
Gere JM . Mechanics of Materials, 5th edn . Beijing : China Machine Press , 2003
[本文引用: 1]
2
2010
... 在材料力学或弹性力学有关功(位移)的互等定理部分有如下或类似的习题[1 -2 ] : ...
... 材料力学中梁弯曲变形的分析基于纯弯曲率公式,忽略了剪切影响并在小变形条件下进一步简化获得挠曲轴方程.经典教材中均提及忽略梁轴线方向的位移[1 ,4 -6 ] (横力弯曲条件下包括曲率缩短与轴线变形),但一般都没有给出各量量级的讨论,此处比较图7 中梁的自由端挠度$w_{A}$,自由端水平位移$\varDelta_{A} $,以及梁轴线长度变化$\Delta l$的量级,对于理解基本概念是有益的(为了符合梁弯曲的图注习惯,下列公式中载荷作用方向的截面横向尺寸改为$h$) ...
Theory of Elasticity, 3rd edn
1
2013
... 在材料力学或弹性力学有关功(位移)的互等定理部分有如下或类似的习题[1 -2 ] : ...
1
2006
... 水平方向位移$\varDelta_{A}$ (如图7 (c))也称为曲率缩短,通过挠曲轴总长与其水平轴投影之差进行计算[3 ] ,通用计算公式是泰勒展开的近似表达 ...
1
2009
... 材料力学中梁弯曲变形的分析基于纯弯曲率公式,忽略了剪切影响并在小变形条件下进一步简化获得挠曲轴方程.经典教材中均提及忽略梁轴线方向的位移[1 ,4 -6 ] (横力弯曲条件下包括曲率缩短与轴线变形),但一般都没有给出各量量级的讨论,此处比较图7 中梁的自由端挠度$w_{A}$,自由端水平位移$\varDelta_{A} $,以及梁轴线长度变化$\Delta l$的量级,对于理解基本概念是有益的(为了符合梁弯曲的图注习惯,下列公式中载荷作用方向的截面横向尺寸改为$h$) ...
1
2003
... 材料力学中梁弯曲变形的分析基于纯弯曲率公式,忽略了剪切影响并在小变形条件下进一步简化获得挠曲轴方程.经典教材中均提及忽略梁轴线方向的位移[1 ,4 -6 ] (横力弯曲条件下包括曲率缩短与轴线变形),但一般都没有给出各量量级的讨论,此处比较图7 中梁的自由端挠度$w_{A}$,自由端水平位移$\varDelta_{A} $,以及梁轴线长度变化$\Delta l$的量级,对于理解基本概念是有益的(为了符合梁弯曲的图注习惯,下列公式中载荷作用方向的截面横向尺寸改为$h$) ...