1 虚铰和无穷远虚铰的运动学特征定理
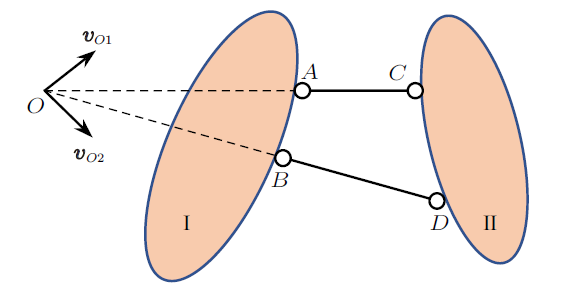
1.1 定理一: 两刚片(或其扩展部分)在虚铰处速度相等
图1
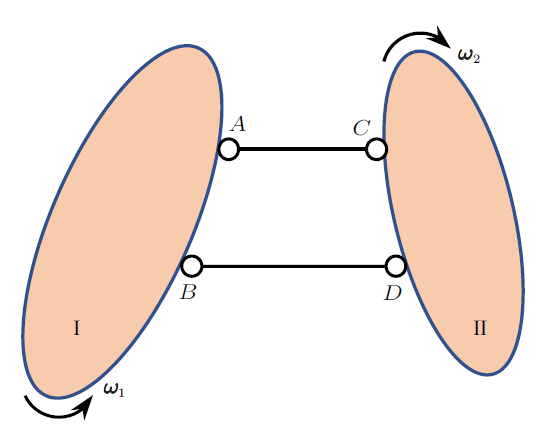
1.2 定理二: 无穷远虚铰(两根平行链杆)连接的两刚片,角速度相等
图2
2 运动学方法分析平面杆件体系几何组成的思路
杆件体系的几何组成分析,又叫机动性分析,本质是考察体系中各刚片之间或者各结点之间有无相对运动的可能,因此可考虑利用运动学的相关理论以及虚铰和无穷远虚铰的运动学特征定理,建立一种杆件体系几何组成分析的新方法。
(1)假设体系可变,并按可能运动的方式,给定体系初始运动参数,如某一个或几个结点(或具有不动点的刚片)的速度$\mathbf v$ (或角速度$\mathbf \omega)$。
(2)利用运动学理论(如基点法、速度瞬心法、速度投影定理等)及本文的两个定理求出其余结点(或刚片)的速度$\mathbf v_{i}$ (或角速度$\mathbf \omega_{i} )$。
(3)分析$\mathbf v$ (或$\mathbf \omega)$是否有非零解,若有非零解则体系几何可变,反之则体系几何不变。
(4)若体系几何不变,求出计算自由度$W$,即可确定体系多余约束的个数。
3 应用举例
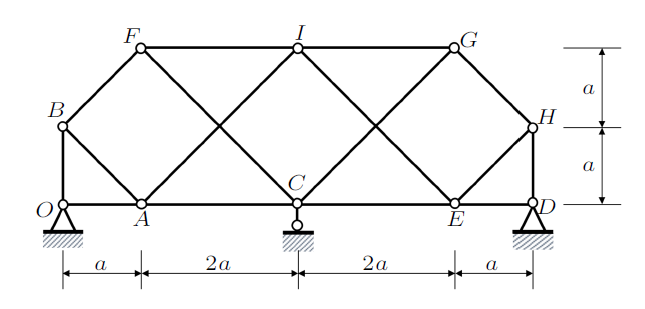
例1 分析图3体系的几何组成。
图3
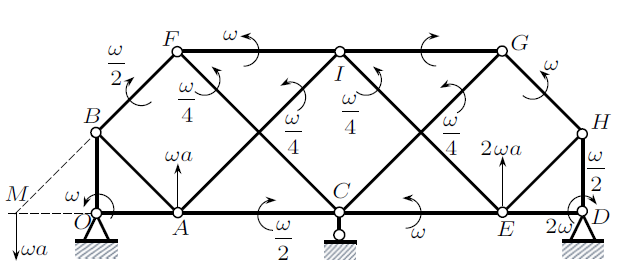
解: (1) $O$和$D$点不动,在$OCD$上利用速度投影定理可知$C$点也不动,设刚片$OAB$绕$O$点转动的角速度为$\omega$,则$A$点及该刚片扩展部分上$M$点的速度均为$\omega a$,见图4。
图4
(2) $M$点是连接刚片$OAB$与杆$CF$的虚铰所在位置,由定理一可得杆$CF$扩展部分上与$M$点重合的点速度也为$\omega a$,于是杆$CF$角速度为
$$ \begin{eqnarray*} \omega_{CF} =\frac{\omega a}{4a}=\frac{\omega }{4} \end{eqnarray*} $$
由于平行链杆连接,由定理二可知杆$AI$, $EI$, $CG$与杆$CF$角速度相等,均为${\omega/4}$。同理,杆$CE$, $FI$, $GH$与刚片$OAB$角速度相等都为$\omega $,可得$E$点速度为$2\omega a$,于是刚片$DEH$的角速度为
(3)由$A$点速度可得杆$AC$角速度为$w/2$,由定理二可知杆$AC$,$BF$,$GI$与刚片$DEH$角速度相等,即
比较式(1)和式(2),得$\omega=0$,可知连接于$O$,$C$和$D$点(已知的不动点)的所有刚片和杆不能动,在此基础上易知其余杆都不动,即体系为几何不变体系。体系的计算自由度$W=-1$,有一个多余约束。
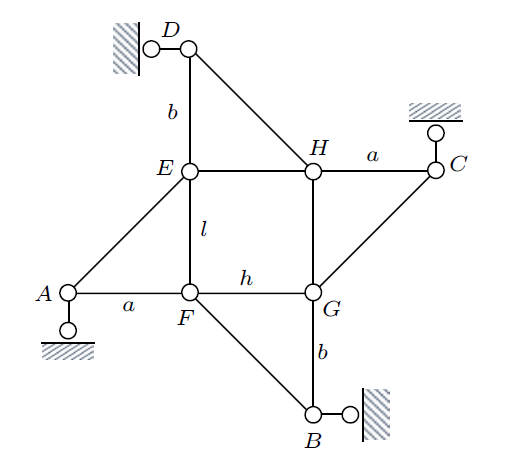
例2 分析图5体系的几何组成。
图5
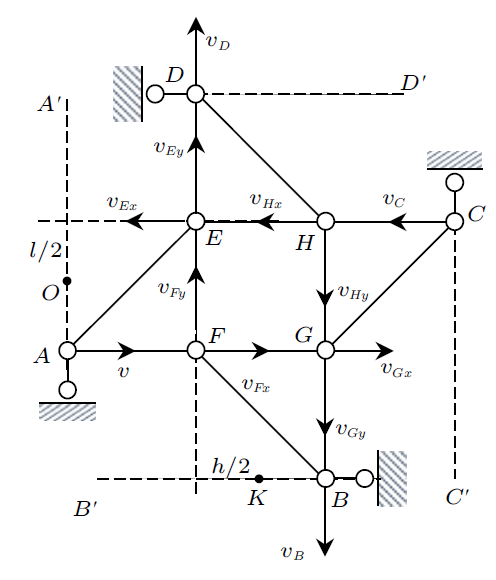
解: (1) 点$A$,$B$,$C$和$D$可分别沿垂直各点支座的方向运动,故刚片$AEF$,$BFG$,$CHG$和$DEH$的速度瞬心分别在直线$AA'$,$BB'$,$CC'$和$DD'$上,见图6,设结点$A$速度为$v$,在$ AFG$上利用速度投影定理,可得刚片$BFG$角速度。
图6
(2) 由定理二可知刚片$BFG$和$DEH$角速度相同,于是可得
根据式(4)及$A$点速度,可确定刚片$AEF$速度瞬心$O$的位置及其角速度,进而可求得点$F$、$E$、$D$沿竖向的速度
$$ \begin{eqnarray*} \omega_{AEF} =\frac{v_{Ex} }{0.5l}=\frac{2v}{l}\Rightarrow v_{Fy} =v_{Ey} =v_{D} =\frac{2va}{l} \end{eqnarray*} $$
(3) 同理可得
$$ \begin{eqnarray*} v_{Hy} =v_{Gy} =v_{B} =\frac{2va}{l} \end{eqnarray*} $$
根据$v_{B}$及$v_{Fy}$可确定刚片$BFG$速度瞬心$K$的位置及其角速度
比较式(3)和式(5),得
$$ \begin{eqnarray*} \omega_{BFG} =\frac{v}{b}=\frac{4va}{hl}\Rightarrow v=0\ \ \mbox{或}\ \ hl=4ab \end{eqnarray*} $$
当$hl=4ab$时,$v$可不为0,即各结点能动,体系几何可变且绝对自由度$S=1$,体系计算自由度$W=0$,故有一个多余约束。当$hl\ne 4ab$时,$v$必为0,即各结点不动,体系几何不变且无多余约束。
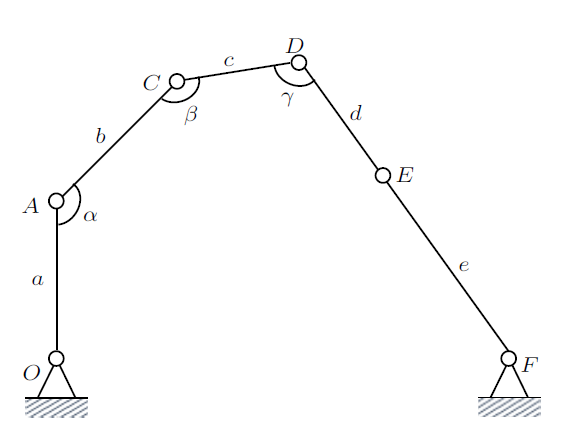
例3 分析图7体系的几何组成。
图7
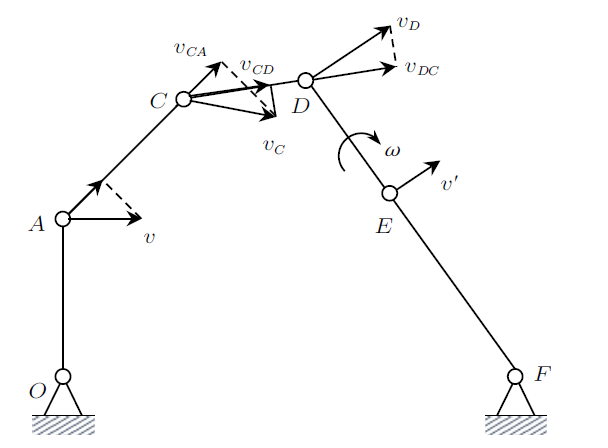
解: (1) $OA$杆和$EF$杆分别可能绕点$O$和$F$转动,可设结点$A$和$E$的速度分别为$v$和${v}'$,并设$EF$杆角速度为$\omega$,见图8,由于$D$,$E$和$F$三点共线且$F$点固定,故$D$点速度$v_{D} $只能垂直于$DEF$,在$ED$上以$E$点为基点,由基点法可得
$$ \begin{eqnarray*} v_{D} ={v}'+\omega d \end{eqnarray*} $$
图8
(2) 分别在$AC$和$CD$上利用速度投影定理,可得$C$点速度$v_{C}$分别沿$AC$和$CD$方向的投影$v_{CA} $和$v_{CD} $
$$ \begin{eqnarray*} v_{CA} =v\sin \alpha,\ \ v_{CD} =v_{D} \sin \gamma =({v}'+\omega d)\sin \gamma \end{eqnarray*} $$
进而可得
$$ \begin{eqnarray*} &&v_{C} =[v^{2}\sin^{2}\alpha +({v}'+\omega d)^{2}\sin^{2}\gamma + \\ &&\qquad 2v({v}'+\omega d)\sin \alpha \sin \gamma \cos \beta ]^{1/2}{\sin \beta } \end{eqnarray*} $$
(3) 各结点速度均已求出,由于$v$,${v}'$和$\omega$均可取任意值,故体系为可变体系,且绝对自由度$S=3$,计算自由度$W=3$,因此无多余约束。
4 需要说明的问题
(1) 对于可变体系,运动学方法不能进一步分析是几何常变还是几何瞬变,实际上大多数时候也不用分析,故统称几何可变[1]。
(2) 对于可变体系,可根据其独立运动参数的个数,确定其绝对自由度$S$,再结合计算自由度$W$,可进一步确定其多余约束的个数为: $S-W$。如例2中,当$hl=4ab$时,$v$可不为0,是可变体系,体系只有一个运动参数$v$,因此$S=1$,结合体系$W=0$,故多余约束有$S-W=1$个。又如例3中,因为有3个独立运动参数$v$,${v}'$和$\omega$,故$S=3$,又因为$W=3$,所以多余约束有$S-W=0$个。
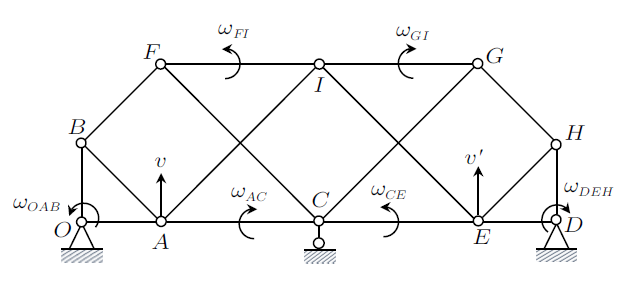
(3) 对于不变体系,只需一个初始运动参数$v$或$\omega $即可求出全部$v_{i}$或$\omega_{i}$;但对于可变体系,往往则需多个初始运动参数才能求出全部$v_{i} $或$\omega_{i}$。由于事先并不确定是哪种体系,因此应根据可能的运动方式,适当多设几个初始运动参数。如例1中,可设结点$A$和$E$的速度分别为$v$和${v}'$,见图9,则有
$$ \begin{eqnarray*} \omega_{OAB} =\frac{v}{a},\ \ \omega_{AC} =\frac{v}{2a},\ \ \omega_{CE} =\frac{{v}'}{2a},\ \ \omega _{DEH} =\frac{{v}'}{a} \end{eqnarray*} $$
图9
由于平行链杆连接,由定理二
$$ \begin{eqnarray*} &&\omega_{OAB} =\omega_{FI} =\omega_{CE} \Rightarrow {v}'=2v\\&& \omega_{AC} =\omega_{GI} =\omega_{DEH} \Rightarrow v=2{v}' \end{eqnarray*} $$
比较两式,有: $v={v}'=0$,即结点$A$和点$E$的速度均为0,不难得出其他结点速度也均为0。
5 结束语
理论力学是结构力学的先学课程,利用已掌握的理论力学中的运动学理论分析平面杆件体系的几何组成,不仅能帮助学生更好理解这一内容,还能解决很多利用两刚片规则、三刚片规则等基本方法不能解决的问题,可作为今后结构力学教学及工程实践的有益补充。
参考文献
平面体系几何组成分析的解析法研究
Study on analytical method of geometric composition analysis for planar system
平面体系几何组成分析广义三角形规则新思路
"虚链杆"在组成分析上的应用
"Virtual bar" used in composition analysis
结合刚体基本运动分析三刚片体系几何构造
Analysis of geometric structure of three-rigid-plate system based on basic motion of rigid body