传统力矩分配法是求解超静定结构的常用手算方法[1 ] ,该法避免了力法和位移法需要求解方程组的缺点,通过逐次分配、传递不平衡力矩来逼近精确解,但是当分配点多于一个时,该方法计算量大且精度有限。针对这一问题,许多学者都提出了力矩分配法的改进方法[2 ] 。刘天一等[3 ] 给出仅含3个分配点结构的力矩分配公式并得到精确解,该方法所给出的公式只适用于3个分配点的情况。刘茂燧等[4 ] 推导了任意跨连续梁杆端转动刚度和结点处力矩传递系数的递推公式,通过一次分配即可求得连续梁的精确解,但该方法计算过程复杂。张宇[5 ] 将结点转角作为迭代目标,仍需较大计算量且存在误差。
本文提出了力矩分配法的方程解法,该方法将渐进的计算过程转化为方程组的求解,方程组的系数矩阵为三对角阵,且主对角线元素始终为"1"。该方程组求解简单,适于少结点问题的手算;对于多结点问题,采用相同顺序的结点编号时,应用该方法可以得到与矩阵位移法形式相同的方程,方程未知量为各分配点的分配力矩代数和,方程的推导不需要单元刚度矩阵的集结。力矩分配法的计算精度随计算轮次的增加而提高,最后收敛于精确解,本文方法将渐进计算过程转化为方程组的求解,因而可以直接得到杆端弯矩的精确解。
力矩分配法是为了避免解算力法和位移法典型方程而发展起来的、简捷的、适于手算的渐进计算方法,但力矩分配法出现了迭代次数和精度的新问题,本文提出的方法解决了这两个新问题。虽然本文方法又回到方程的求解,但是一方面该方法所需解算的方程较力法和位移法典型方程更为简单,另一方面,本文方法其实正是力矩分配法向矩阵位移法的过渡,该方法让我们进一步理解,从想摆脱方程求解,到回到方程求解的必要性,在教学中指出这一必要性,有助于学生乐于接受更繁琐的矩阵位移法。此外,对于多结点问题,相比于矩阵位移法,本文方法的方程建立过程更简洁,有助于启发学生的编程思维及相应的计算练习。
1 力矩分配法的方程解法原理
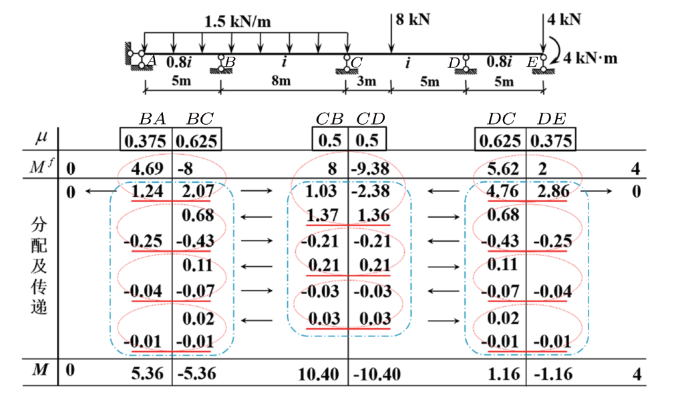
传统的力矩分配法只适用于求解无侧移结构,以李廉锟[1 ] 书中例9-2含有3个分配点的连续梁为例,说明力矩分配法方程解法的原理。
观察图1 计算表格,每个椭圆圈内所有数的代数和为"0";$B$左侧截面只有分配力矩,$B$右侧截面则既有分配力矩又有传递力矩,$D$结点与$B$结点情况相反,$C$为中间的分配点,两侧均有分配力矩和传递力矩。由上述观察可知,$B$点两侧所有传递力矩和分配力矩的代数和等于$B$两侧截面固端力矩代数和的相反数,$C$和$D$两结点处也有相同的结论,即矩形框内所有数值的代数和等于各结点两侧截面固端力矩代数和。
图1
设$B$,$C$,$D$三个分配点处各次分配力矩的代数和分别为$M_{B}$,$M_{C}$和$M_{D}$,同时考虑各结点所连杆端分配系数代数和为"1", 则有
(1) $\left. \begin{array}{l} M_{B}+C_{CB}\mu_{CB}M_{C}=-M_{B}^{f} \\ {C_{BC}\mu_{BC}M_{B}+M}_{C}+C_{DC}\mu_{DC}M_{D}=-M_{C}^{f} \\ C_{CD}\mu_{CD}M_{C}+M_{D}=-M_{D}^{f} \\ \end{array} \right\}$
该方程组主对角线元素均为"1",求解方程组可得三个分配点处各次分配力矩的代数和${M}_{{B}}$,${M}_{{C}}$和${M}_{{D}}$。分配点杆端弯矩可按式(2)计算
(2) $M_{ij}=M_{ij}^{f}+\mu_{ij}M_{i}+C_{ji}\mu_{ji}M_{j}(i,j=B,C,D)$
非分配点$A$和$E$的杆端弯矩数值,等于求解方程组得到的相邻分配点分配力矩代数和乘以相应传递系数,再叠加截面相应的固端弯矩数值。
2 力矩分配法的方程解法算例
为方便对比,仍以李廉锟[1 ] 书中例9-2为例,用力矩分配法的方程解法计算各杆端弯矩。
由力矩分配法的方程解法计算过程可知,该方法将传统的渐进计算过程转化为三对角矩阵方程组的求解,简化了计算步骤及计算工作量,并得到精确解。
(3) $\left.\begin{array}{l}6.4 i \theta_{B}+2 i \theta_{C}=3.31 \\2 i \theta_{B}+8 i \theta_{C}+2 i \theta_{D}=1.38 \\2 i \theta_{C}+6.4 i \theta_{D}=-7.62\end{array}\right\}$
对比方程(3)与图2 计算表格中的方程可知,两方程形式一致,但推导过程及未知量完全不同,本文解法给出的方程主对角线元素均为"1",求解更简单。
图2
3 力矩分配法的方程解法一般方程及其解
对有$n$个分配点的多跨梁或单层无侧移刚架,力矩分配法的方程解法即求解式(4)中系数矩阵为三对角阵,且主对角线元素均为"1"的方程组。
(4) $\begin{array}{l}M_{1}+C_{21} \mu_{21} M_{2}+0+\cdots+0=\\-M_{1}^{f}\\C_{12} \mu_{12} M_{1}+M_{2}+C_{32} \mu_{32} M_{3}+\\0+\cdots+0=-M_{2}^{f}\\0+C_{23} \mu_{23} M_{2}+M_{3}+C_{43} \mu_{43} M_{4}+\\0+\cdots+0=-M_{3}^{f}\\0+\cdots+0+C_{(n-2)(n-1)} \mu_{(n-2)(n-1)} \text {. }\\M_{(n-2)}+M_{(n-1)}+C_{n(n-1)} \mu_{n(n-1)} \text {. }\\M_{n}=-M_{(n-1)}^{f}\\0+\cdots+0+C_{(n-1) n} \mu_{(n-1) n} M_{(n-1)}+\\M_{n}=-M_{n}^{f}\end{array}$
其中${C}_{{ij}}$,${\mu}_{{ij}}$及${M}_{{i}}^{{f}}$均为题目的已知条件,求解方程得到$M_{i}$ ($i=1$,2,$\cdots$,$n$),各分配点杆端弯矩表达式为
(5) $M_{ij}=M_{ij}^{f}+\mu_{ij}M_{i}+C_{ji}\mu_{ji}M_{j}$
非分配点杆端弯矩等于固端弯矩加上相邻分配点传来的传递力矩。
对于多分配点连续梁问题及如图3 (a)所示的只有一层结点的无侧移刚架问题,上述方法将一般力矩分配法的渐进计算过程转化为三对角矩阵方程组的求解,在不改变力矩分配法的分析思路,保留杆端弯矩作为分析对象的同时,极大简化了计算步骤及计算工作量,并得到精确解。
图3
对于图3 (b)所示的两层无侧移刚架,或其他的多层无侧移刚架,应用本文方法仍可快速写出需要求解的方程组,此时的系数矩阵主对角元素仍为"1",带宽取决于各结点的编号顺序。关于本文方法求解多层无侧移刚架及与矩阵位移法的对比还可以进行进一步的讨论。
4 结论
本文提出了力矩分配法的方程解法,该方法适用于所有可用力矩分配法求解的无侧移结构。对于较多分配点的连续梁问题及各分配点连接较多杆件的单层无侧移刚架问题,该方法可简化计算步骤,提高计算效率,并得到问题的精确解。
在教学中,本文提出的方法没有增加新的参数,易于学生的理解、接受和应用;力矩分配法与矩阵位移法都是在位移法的基础上发展起来的,力矩分配法直接以杆端弯矩作为分析对象,采用本文方法可以将问题转化为方程组的求解,由此可以引导学生思考,是否可以在将结点位移作为基本未知量的求解过程中,同样引入适于计算机处理的方程解法,而这一思想正是矩阵位移法基本思路,因此本文方法有助于拓展学生的解题思路,引发学生的深入思考,提高学习积极性。
参考文献
View Option
[2]
杨光华 . 精确力矩分配法、各种近似广义力矩分配法及一般力矩分配法统一的数学原理
沈阳建筑工程学院学报 , 1985 (1 ):34 -41
[本文引用: 1]
[3]
刘天一 , 陈素文 . 含3个分配点结构的弯矩分配公式法精确解
力学与实践 , 2014 , 36 (2 ):207 -209
[本文引用: 1]
Liu Tianyi Chen Suwen . Moment distribution formula method to seek exact solution of structures with three distribution points
Mechanics in Engineering 2014 , 36 (2 ):207 -209 (in Chinese)
[本文引用: 1]
[4]
刘茂燧 , 程渭民 . 一次性分配的力矩分配法
力学与实践 , 2007 , 29 (4 ):73 -75
[本文引用: 1]
Liu Maosui Cheng Weimin . Moment distribution method of one-off distribution
Mechanics in Engineering 2007 , 29 (4 ):73 -75 (in Chinese)
[本文引用: 1]
[5]
张宇 . 连续梁的多结点力矩分配法
力学与实践 , 2003 , 25 (5 ):77 -80
[本文引用: 1]
Zhang Yu . A multi-joint moment distribution method for continuous beams
Mechanics in Engineering 2003 , 25 (5 ):77 -80 (in Chinese)
[本文引用: 1]
3
2010
... 传统力矩分配法是求解超静定结构的常用手算方法[1 ] ,该法避免了力法和位移法需要求解方程组的缺点,通过逐次分配、传递不平衡力矩来逼近精确解,但是当分配点多于一个时,该方法计算量大且精度有限.针对这一问题,许多学者都提出了力矩分配法的改进方法[2 ] .刘天一等[3 ] 给出仅含3个分配点结构的力矩分配公式并得到精确解,该方法所给出的公式只适用于3个分配点的情况.刘茂燧等[4 ] 推导了任意跨连续梁杆端转动刚度和结点处力矩传递系数的递推公式,通过一次分配即可求得连续梁的精确解,但该方法计算过程复杂.张宇[5 ] 将结点转角作为迭代目标,仍需较大计算量且存在误差. ...
... 传统的力矩分配法只适用于求解无侧移结构,以李廉锟[1 ] 书中例9-2含有3个分配点的连续梁为例,说明力矩分配法方程解法的原理. ...
... 为方便对比,仍以李廉锟[1 ] 书中例9-2为例,用力矩分配法的方程解法计算各杆端弯矩. ...
精确力矩分配法、各种近似广义力矩分配法及一般力矩分配法统一的数学原理
1
1985
... 传统力矩分配法是求解超静定结构的常用手算方法[1 ] ,该法避免了力法和位移法需要求解方程组的缺点,通过逐次分配、传递不平衡力矩来逼近精确解,但是当分配点多于一个时,该方法计算量大且精度有限.针对这一问题,许多学者都提出了力矩分配法的改进方法[2 ] .刘天一等[3 ] 给出仅含3个分配点结构的力矩分配公式并得到精确解,该方法所给出的公式只适用于3个分配点的情况.刘茂燧等[4 ] 推导了任意跨连续梁杆端转动刚度和结点处力矩传递系数的递推公式,通过一次分配即可求得连续梁的精确解,但该方法计算过程复杂.张宇[5 ] 将结点转角作为迭代目标,仍需较大计算量且存在误差. ...
含3个分配点结构的弯矩分配公式法精确解
1
2014
... 传统力矩分配法是求解超静定结构的常用手算方法[1 ] ,该法避免了力法和位移法需要求解方程组的缺点,通过逐次分配、传递不平衡力矩来逼近精确解,但是当分配点多于一个时,该方法计算量大且精度有限.针对这一问题,许多学者都提出了力矩分配法的改进方法[2 ] .刘天一等[3 ] 给出仅含3个分配点结构的力矩分配公式并得到精确解,该方法所给出的公式只适用于3个分配点的情况.刘茂燧等[4 ] 推导了任意跨连续梁杆端转动刚度和结点处力矩传递系数的递推公式,通过一次分配即可求得连续梁的精确解,但该方法计算过程复杂.张宇[5 ] 将结点转角作为迭代目标,仍需较大计算量且存在误差. ...
含3个分配点结构的弯矩分配公式法精确解
1
2014
... 传统力矩分配法是求解超静定结构的常用手算方法[1 ] ,该法避免了力法和位移法需要求解方程组的缺点,通过逐次分配、传递不平衡力矩来逼近精确解,但是当分配点多于一个时,该方法计算量大且精度有限.针对这一问题,许多学者都提出了力矩分配法的改进方法[2 ] .刘天一等[3 ] 给出仅含3个分配点结构的力矩分配公式并得到精确解,该方法所给出的公式只适用于3个分配点的情况.刘茂燧等[4 ] 推导了任意跨连续梁杆端转动刚度和结点处力矩传递系数的递推公式,通过一次分配即可求得连续梁的精确解,但该方法计算过程复杂.张宇[5 ] 将结点转角作为迭代目标,仍需较大计算量且存在误差. ...
一次性分配的力矩分配法
1
2007
... 传统力矩分配法是求解超静定结构的常用手算方法[1 ] ,该法避免了力法和位移法需要求解方程组的缺点,通过逐次分配、传递不平衡力矩来逼近精确解,但是当分配点多于一个时,该方法计算量大且精度有限.针对这一问题,许多学者都提出了力矩分配法的改进方法[2 ] .刘天一等[3 ] 给出仅含3个分配点结构的力矩分配公式并得到精确解,该方法所给出的公式只适用于3个分配点的情况.刘茂燧等[4 ] 推导了任意跨连续梁杆端转动刚度和结点处力矩传递系数的递推公式,通过一次分配即可求得连续梁的精确解,但该方法计算过程复杂.张宇[5 ] 将结点转角作为迭代目标,仍需较大计算量且存在误差. ...
一次性分配的力矩分配法
1
2007
... 传统力矩分配法是求解超静定结构的常用手算方法[1 ] ,该法避免了力法和位移法需要求解方程组的缺点,通过逐次分配、传递不平衡力矩来逼近精确解,但是当分配点多于一个时,该方法计算量大且精度有限.针对这一问题,许多学者都提出了力矩分配法的改进方法[2 ] .刘天一等[3 ] 给出仅含3个分配点结构的力矩分配公式并得到精确解,该方法所给出的公式只适用于3个分配点的情况.刘茂燧等[4 ] 推导了任意跨连续梁杆端转动刚度和结点处力矩传递系数的递推公式,通过一次分配即可求得连续梁的精确解,但该方法计算过程复杂.张宇[5 ] 将结点转角作为迭代目标,仍需较大计算量且存在误差. ...
连续梁的多结点力矩分配法
1
2003
... 传统力矩分配法是求解超静定结构的常用手算方法[1 ] ,该法避免了力法和位移法需要求解方程组的缺点,通过逐次分配、传递不平衡力矩来逼近精确解,但是当分配点多于一个时,该方法计算量大且精度有限.针对这一问题,许多学者都提出了力矩分配法的改进方法[2 ] .刘天一等[3 ] 给出仅含3个分配点结构的力矩分配公式并得到精确解,该方法所给出的公式只适用于3个分配点的情况.刘茂燧等[4 ] 推导了任意跨连续梁杆端转动刚度和结点处力矩传递系数的递推公式,通过一次分配即可求得连续梁的精确解,但该方法计算过程复杂.张宇[5 ] 将结点转角作为迭代目标,仍需较大计算量且存在误差. ...
连续梁的多结点力矩分配法
1
2003
... 传统力矩分配法是求解超静定结构的常用手算方法[1 ] ,该法避免了力法和位移法需要求解方程组的缺点,通过逐次分配、传递不平衡力矩来逼近精确解,但是当分配点多于一个时,该方法计算量大且精度有限.针对这一问题,许多学者都提出了力矩分配法的改进方法[2 ] .刘天一等[3 ] 给出仅含3个分配点结构的力矩分配公式并得到精确解,该方法所给出的公式只适用于3个分配点的情况.刘茂燧等[4 ] 推导了任意跨连续梁杆端转动刚度和结点处力矩传递系数的递推公式,通过一次分配即可求得连续梁的精确解,但该方法计算过程复杂.张宇[5 ] 将结点转角作为迭代目标,仍需较大计算量且存在误差. ...