地基在移动荷载作用下的动力响应一直是岩土工程和交通工程领域的重点关注课题。随着运输业的发展,车辆的行驶速度越来越快,载重也越来越大,在此背景下研究地基土在移动荷载作用下动力响应问题对于道路结构设计和环境振动影响分析都具有重要意义。地基土体是一种具有多相组成和骨架孔隙结构的复杂介质,在动力作用下由于土体内部存在多场耦合效应,使其动力响应分析变得非常复杂。将地基土体视为固体骨架和孔隙水组成的两相饱和介质,利用Biot多孔介质波动理论进行动力响应分析已经相当成熟^[1-4]。徐斌等^[5]根据Biot波动理论,采用传递、反射矩阵方法研究了移动荷载作用下层状饱和土动力响应问题。王立安等^[6]对非均匀饱和地基的动力特性做了研究。徐长节等^[7]和周凤玺等^[8]基于Vardoulakis等^[9]的理论研究了非饱和土中波的传播规律。李绍毅^[10]采用半解析法研究了移动荷载作用下多层非饱和铁路地基的共振问题,分析了土体饱和度对非饱和地基振动的影响。Lu等^[11]研究了矩形移动荷载作用下非饱和地基的动力响应。Fang等^[12]研究了列车荷载作用下非饱和地基的振动响应。Song等^[13]对埋置荷载作用下的非饱和地基动力响应问题做了研究。

上述关于非饱和地基的动力响应研究中,学者们都将地基考虑为单层非饱和介质,而实际自然界中的地基由于地下水的存在,地基底部土体往往是完全饱和的,只有顶部一定深度范围内受到环境气候的影响表现为非饱和状态。因此,对地基进行更精确的理论分析时,应将地基考虑为由下层饱和土和上层非饱和土层叠而成的半空间。

基于以上分析,文中将地基考虑为饱和土和非饱和土层叠而成的半空间模型,利用三重Fourier变换和降阶法对饱和土和非饱和土的控制方程进行耦合求解,推导出地基在矩形移动荷载作用下的动力响应解。通过算例分析,对模型验证计算并给出了地表位移峰值沿上层非饱和土体饱和度和土层厚度的变化规律曲线,同时也给出了矩形移动荷载作用下地表($z=0$)竖向位移的空间分布及竖向振动峰值与速度的关系曲线。

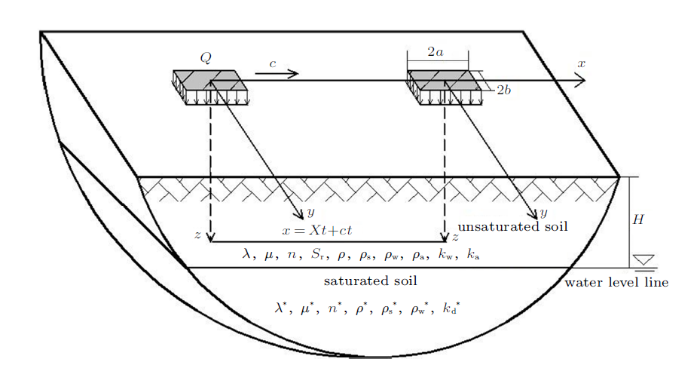
如图1所示,由非饱和土和饱和土层叠而成的半空间表面作用一矩形移动荷载$Q$,荷载移动速度为$c$,荷载分布长、宽分别为2$a$和2$b$。上层非饱和土厚度为$H$,下层饱和土为无限厚度。 图中,$\lambda^{\ast }$, $\mu^{\ast}$为饱和土对应的Lamb常数,其表达式分别为

$\lambda^{\ast }=\dfrac{E^{\ast}\nu^{\ast }}{\left( {1+\nu^{\ast }} \right)\left( {1-2\nu^{\ast }}\right)},\ \mu^{\ast }=\dfrac{E^{\ast }}{2\left( {1+\nu^{\ast }}\right)}$

式中$E^{\ast }$和$\nu^{\ast }$分别为弹性模量和泊松比。$n^{\ast }$, $k_{\rm d}^{\ast }$, $\rho^{\ast }$, $\rho_{\rm s}^{\ast }$, $\rho_{\rm w}^{\ast}$分别为饱和土的孔隙率、渗透系数、饱和土的总质量密度、固相密度和水相密度;$\lambda$和$\mu $为对应于非饱和土的Lamd常数;$n$和$S_{\rm r}$分别为孔隙率和饱和度;$k_{\rm w}$,$k_{\rm a}$分别为非饱和土中孔隙水和气体的渗透系数。对于非饱和土的总质量密度$\rho$有

式中,$\rho_{\rm s}$,$\rho_{\rm w}$和$\rho _{\rm a}$分别为非饱和土中固体、水和气体的质量密度。

根据混合物理论,考虑固-液-气之间的惯性耦合及毛细管压力,非饱和土的运动方程写为^[12-13]

式中,$u$为非饱和土体中固体骨架的位移矢量($u_{i}$,$i=x$, $y$, $z$);$w$,$v$分别为孔隙中水相和气相相对于固体骨架的相对位移矢量;$\theta$为固体骨架的体应变。“($^{{\cdot }})$”、“($^{{\cdot \cdot}})$”表示对时间$t$的一、二阶导数。$p_{\rm w}$,$p_{\rm a}$分别为孔隙水压力和孔隙气压力;$\alpha $为Biot系数,$\alpha=1-K_{\rm sf}/K_{\rm s}$,其中$K_{\rm sf}$和$K_{\rm s}$是土骨架和土颗粒的体积模量,$\lambda + 2\mu /3= K_{\rm sf}$;$\chi $为有效应力参数,取值与有效饱和度$S_{\rm e}$相同,$S_{\rm e}$的表达式为：$S_{\rm e}=(S_{\rm r}-S_{\rm w0})/(1-S_{\rm w0})$,其中$S_{\rm w0}$为束缚水饱和度(或残余饱和度);$g$为重力加速度。$\nabla$和$\nabla^{2}$分别为Hamilton算子和Laplace算子,即：$\nabla={\partial /x}+{\partial /y}+{\partial /z}$,$\nabla^{2}={{\partial^{2}}/{x^{2}}}+{{\partial^{2}}/{y^{2}}}+{{\partial^{2}}/{z^{2}}}$。对于非饱和土的总孔隙压力$p$,有

根据有效应力原理,非饱和土本构关系写为^[13]

式中,$\sigma_{ij}$ ($i,j=x,y,z$)为总应力,$\varepsilon_{ij}$是应变张量,$\delta_{ij}$为Kronecker符号。

式中,$A_{11}$$\sim$$A_{14}$, $A_{21}$$\sim$$A_{24}$见参考文献[13]。

对于Hamilton算子$\nabla $,有如下散度计算式

式中,$\theta_{\rm w}$和$\theta_{\rm a}$分别为孔隙水和气体的体应变。

对空间坐标$x$,$y$和时间坐标$t$引入三重Fourier变换,其变换关系为

式中,$\xi $,$\eta$,$s$分别为对应于$x$,$y$,$t$的变换参数;$\tilde{{\tilde{{\tilde{{f}}}}}}$表示对应场量的三重Fourier变换。

利用式(10)对式(2)$\sim$式(9)进行三重Fourier变换和算子运算,并通过降阶法求解常微分方程组得到非饱和土的位移、孔压及应力通解,详细解法参见文献[11-12,14-15]。

式中,$\varTheta$为特征向量矩阵;$\pm\gamma_{1}$,$\pm\gamma_{2}$, $\ldots$, $\pm\gamma_{5}$为矩阵$\varTheta$对应的特征根;$D_{1}$$\sim$$D_{10}$为积分常数,通过边界条件确定。

由Biot波动理论,饱和土动力控制方程为^[16]

(1)运动方程

(2)本构方程

(3)渗流连续方程

式中各参数定义参见文献[16],其中上标“*”表示饱和土对应的物理量。

采用与非饱和土相同的求解方法,同样利用Fourier变换和散度运算求解饱和土控制方程,再采用降阶法求解常微分方程组可得出饱和土的通解。此处,直接给出饱和土在变换域中的位移、孔隙压力和应力通解。

式中,$\varXi$为特征向量矩阵;$\gamma_{1}^{\ast }$,$\gamma_{2}^{\ast }$,$\gamma_{3}^{\ast}$,$\gamma_{4}^{\ast }$为矩阵$\varXi$对应的负的特征根,因为,由于下层饱和土为无限半空间,因此求解饱和土控制方程时应根据波的辐射条件将正指数项舍去;$D_{11}$$\sim$$D_{14}$为积分常数,通过边界条件确定。

对于半空间顶面作用的移动矩形分布荷载$Q$,利用Heaviside阶跃函数将其写为

式中,$H$( )表示Heaviside阶跃函数;$q_{0} $为荷载集度。

对式(18)做三重Fourier变换,得到

式中,$\delta $( )表示Dirac-delta函数。

地表为透水、透气边界,则半空间表面($z=0$)处的边界条件为

由于下层为饱和土,所以上层非饱和土中的水、气不能向下渗透,故土层交界面($z=H$)处的连续条件为

通过边界条件和连续条件组成的14个方程可确定出积分常数$D_{1}$$\sim$$D_{14}$。对式(20)和式(21)做三重Fourier变换,再将饱和土和非饱和土的位移、应力和孔压的通解代入,并分别取$z=$0,$z=H$,得到关于$D_{1}$$\sim$$D_{14}$的线性方程组

式中, $\varPhi $为$14\times14$的系数矩阵,其矩阵元素 $\varPhi_{11}$$\sim$$\varPhi_{1414}$见附录。利用矩阵运算可确定出$D_{1}$$\sim$$D_{14}$的结果为

至此,系统中所有参数均已确定。将$D_{1}$$\sim$$D_{14}$回代到式(11)、式(12)和式(16)、式(17),即可计算出非饱和土层和饱和土层中的位移、应力和孔隙压力。对计算结果做Fourier逆变换,可得到时间-空间域中各场量的计算结果。

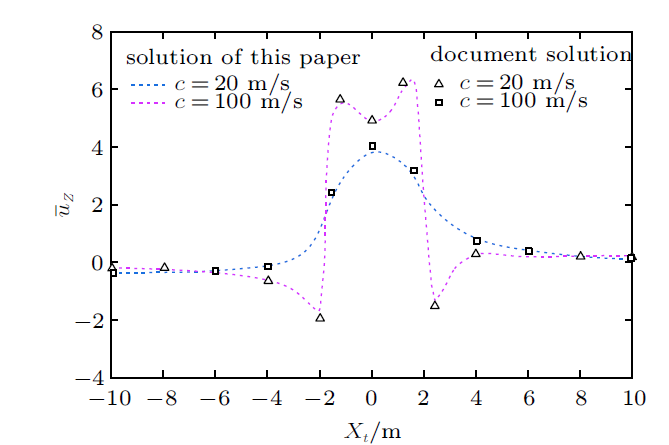
对前文推导结果进行编程计算,关于式(11)、式(12)和式(16)、式(17)的Fourier逆变换可通过数值积分或离散Fourier逆变换实现,本文中采用计算效率较高的离散Fourier逆变换实现。引入移动坐标轴$X_t$,$X_t=x-ct$,使计算结果能以振源为中心分布。取上层非饱和土的饱和度$S_{\rm r}=1$,则半空间地基退化为单一饱和半空间,此时,有效应力参数$\chi=1$。则上、下层土体的特性参数值相同,土体参数取值与文献[16]相同,按文献[16]给定计算参数进行取值计算,其中主要参数的取值有：Lamb常数$\mu$取30 MPa,$n$取0.3;非饱和土中固体和水的质量密度$\rho_{\rm s}$和$\rho_{\rm w}$的取值分别为2700 kg/m$^{3}$和1000 kg/m$^{3}$。图2为本文退化解与单层饱和半空间模型[16]的结果对比,图中显示,退化解与文献解能够很好地吻合。(图中$\bar{{u}}_{z}$为无量纲竖向位移,$\bar{{u}}_{z} ={{u_{z} \mu^{\ast }}/{\left( {aq_{0} }\right)}}$。)

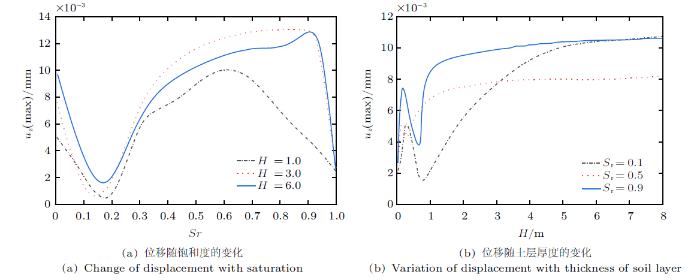
图3为移动荷载作用下地表($z=0$)竖向位移的空间分布。图4为地表位移峰值沿上层非饱和土体饱和度和土层厚度的变化规律曲线。图4(a)显示：当非饱和土层饱和度小于0.15时,地表位移峰值随饱和度的增大而急速减小,当非饱和土层饱和度大于0.15时则随之增大,当非饱和土层饱和度接近0.9时(趋于完全饱和)则再次急速减小,曲线的拐点位置随非饱和土层的厚度发生变化。图4(b)显示：当非饱和土层的厚度小于0.5 m时,地表振动位移发生剧烈波动。当非饱和土层的厚度大于0.5 m时,随着非饱和土层的厚度增大,地表位移也随之增大。但当非饱和土层达到一定厚度后,振动位移将收敛于恒定值,该收敛值与单层非饱和地基的结果一致,说明地基完全体现为单层非饱和土地基,不再受下部饱和土层的影响,该临界厚度与土体饱和度相关,还能看出当地基上层土体为中度饱和时,层状土对地表位移峰值的影响较小。

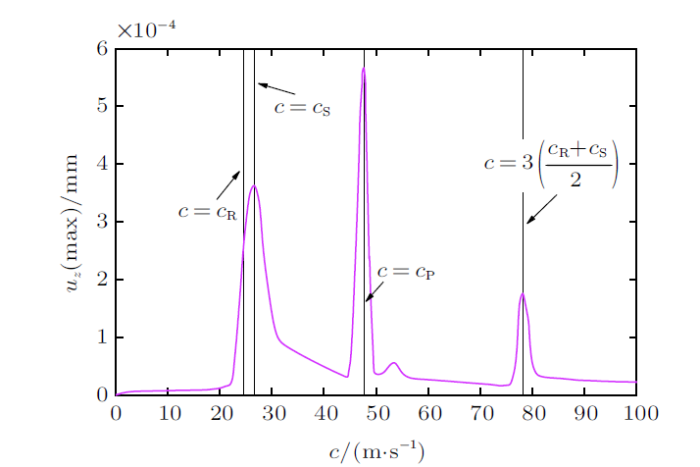
图5为竖向振动峰值与速度的关系曲线,从图中可以看出,当荷载移动速度小于$c_{\rm R}$时,竖向振动峰值很小,随着速度的增大竖向振动峰值发生小幅增涨,但当荷载速度达到$c_{\rm R}$时,竖向振动发生激增,当速度等于$c_{\rm S}$时出现第一个峰点。随着速度进一步增大,在$c=c_{\rm P}$,$c=3\left[(c_{\rm R} +c_{\rm S})/{2}\right]$时,再次出现峰点,且$c=c_{\rm P}$时为最大峰值点。其中：$c_{\rm S}$为地震横波波速,$c_{\rm S}=\sqrt{{E}/[{2\rho \left( {1+\nu } \right)}]}$;$c_{\rm P}$为地震纵波波速,$c_{\rm P} =\sqrt{{E\left( {1-\nu } \right)}/[{\rho\left( {1+\nu } \right)\left( {1-2\nu } \right)}]}$;$c_{\rm R}$为瑞利波速,$c_{\rm R} =({0.862+1.14\nu })/({1+\nu })\cdot c_{\rm S}$;式中,$E$,$\nu $为弹性常数,$\rho $为介质密度。

将地基考虑为饱和-非饱和土双层半空间,利用Dirac-delta函数和Heaviside阶跃函数将矩形移动荷载描述为时间和空间坐标的解析函数,采用三重Fourier变换和降阶法推导出矩形移动荷载作用下饱和-非饱和土双层地基中各场量的解析解。通过算例分析,总结出以下结论。

(1) 随着上层非饱和土厚度的增大,地表振动位移也随之增大,层厚处于0$\sim$0.5 m时,地表振动位移发生剧烈波动。

(2) 地基上层土体为中度饱和时,层状土的影响将减小。

(3) 当荷载移动速度小于瑞利波速时,竖向振动峰值很小,振幅随速度的增大发生小幅增涨,但当荷载速度达到瑞利波速时,竖向振动发生激增;随着速度进一步增大,竖向位移多次出现峰点。

$ \begin{align} \varPhi_{1j} ={i}\lambda \left( {\xi \phi_{1j} +\eta \phi_{2j} } \right)+r_{k}\left( {\lambda +2\mu } \right)\phi_{3j} -\alpha \chi \phi_{4j} - \\ \alpha\left( {1-\chi } \right)\cdot\phi_{5j}\ (j=1,2,\ldots, 14; k=1,2,\ldots, 10;\\ j=11,12,\ldots, 14, \varPhi_{1j}=0); \end{align} $

$\varPhi_{2j} =\mu \left( {i\xi \phi_{3j} +r_{k} \phi_{1j} } \right)\ (j=1,2,\ldots, 14; k=1,2,\ldots, 10;\\ j=11,12,\ldots, 14, \varPhi_{ij} =0);$

$\varPhi_{3j} =\mu \left( {i\eta \phi_{3j} +r_{k} \phi_{2j} }\right)\ (j=1,2,\ldots, 14; k=1,2,\ldots, 10;\\ j=11,12,\ldots, 14, \varPhi_{ij} =0);$

$\varPhi_{ij} =\phi_{ij}\ (i=4,5; j=1,2,\ldots, 14; j=11,12,\ldots, 14,\\ \varPhi_{ij} =0);$

$\begin{align} \varPhi_{ij} =\left\{ {\begin{array}{ll} \phi_{i-5,j} {\rm e}^{r_{k} H} & \left( {j=1,2,..., 10;k=1,2,..., 10} \right) \\ -\phi_{i-5,j}^{\ast } {\rm e}^{r_{k}^{\ast } H}& \left( {j=11,12,..., 14;k=1,2,..., 4} \right) \\ \end{array}} \right. \\ (i=6,7,8); \end{align}$

$\varPhi_{ij} =\left\{ \begin{array}{l} \phi_{i-8,j} {\rm e}^{r_{k} H}\\ \left( {i=9,10,11;j=1,2,..., 10;k=1,2,..., 10} \right) \\ \left.\begin{array}{l} -\Big[ {i}\lambda^{\ast }\left( {\xi \phi_{i-8,j-10}^{\ast } +\eta \phi_{i-7,j-10}^{\ast } } \right)+\\ r_{k}^{\ast } \left( {\lambda^{\ast }+2\mu^{\ast }} \right)\phi_{i-6,j-10}^{\ast } - \\ \phi_{i-5,j-10}^{\ast }\Big]{\rm e}^{r_{k}^{\ast } H}\\ \left( {i=9} \right) \\ -\mu^{\ast }\Big( i\xi \phi_{i-7,j-10}^{\ast } +\\ r_{k}^{\ast } \phi_{i-9,j-10}^{\ast } \Big){\rm e}^{r_{k}^{\ast } H}\ \left( {i=10} \right) -\mu^{\ast }\Big( i\eta \phi_{i-8,j-10}^{\ast } +\\ r_{k}^{\ast } \phi_{i-9,j-10}^{\ast } \Big){\rm e}^{r_{k}^{\ast } H}\ \left( {i=11} \right) \end{array}\right\} \\ \left( {j=11,12,..., 14;k=1,2,..., 4} \right) \end{array} \right.;$

$\varPhi_{ij} =\left\{ {\begin{array}{l} \left[ {\chi \phi_{i-8,j} +\left( {1-\chi } \right)\phi_{i-7,j} } \right]{\rm e}^{r_{k} H}\\ \left( {j=1,2,..., 10;k=1,2,..., 10} \right) \\ -\phi_{i-8,j-10}^{\ast } \cdot {\rm e}^{r_{k}^{\ast } H}\\ \left( {j=11,12,..., 14;k=1,2,..., 4} \right) \\ \end{array}} \right.\ (i=12);$

$\begin{align} \varPhi_{ij} =r_{k} \phi_{i-9,j} \cdot {\rm e}^{r_{k}H}\ (i=13,14; j=1,2,\ldots, 14;\\ k=1,2,\ldots, 10; \mbox{当} j=11,12,\ldots, 14\mbox{时}, \varPhi_{ij}=0)\\ (r_{1}=-r_{2}, r_{3}=-r_{4}, r_{5}=-r_{6}, r_{7}=-r_{8}, r_{9}=-r_{10}). \end{align}$