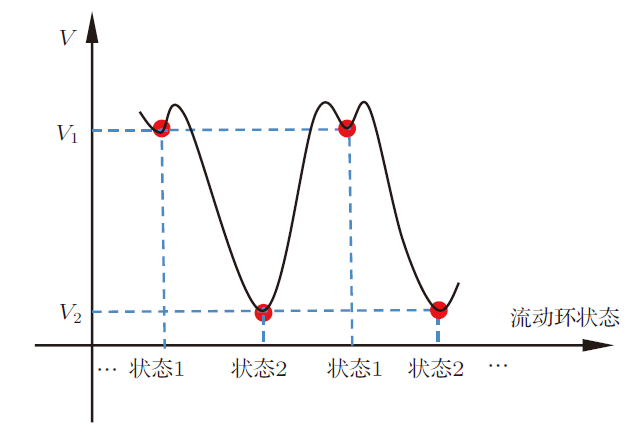
一种称为流动环(toroflux)的玩具备受关注。它是由一根细长钢带缠绕形成的接近于多个圆环互相连接构成的封闭的螺旋状形体。由直钢带弯曲为螺旋带的制造工艺使内部产生预应力[1-2]。流动环存在合拢和张开两种平衡状态,分别记为状态1和状态2,是典型的双稳态系统(图1)。两种状态皆为稳定,但状态1的稳定性极易转变为不稳定,受微小扰动即瞬间转变为状态2。另一独特现象是将其套在手臂上自由下落时,即自动从静止转变为绕手臂旋转。角速度不断升高,在光线作用下如同流水形成的银色气泡,流动环因此得名(图2)。关于流动环的具体构造和简明的物理解释本刊已有文章说明[2]。 本文对流动环的运动做更深入的动力学分析,对上述形态突变和下落旋转两种现象提出更确切的理论解释。

流动环的两种平衡状态具有不同的弹性变形势能。依据弹性体平衡的最小势能原理,其状态变化应朝向势能减小的方向进行[3]。要计算弹性变形势能,首先必须确定两种状态的几何形态。

流动环作为特殊的封闭曲杆,应遵循曲杆变形的普遍规律。20世纪60年代,Calugareanu G (1961), White JH (1969) 等提出利用缠绕数$W_{\rm r}$、扭转数$T_{\rm w}$和连接数$L_{\rm k}$作为描述曲杆变形的几何参数。证明了连接数$L_{\rm k}$是封闭曲杆或两端固定曲杆变形的不变量,且满足以下White公式

根据分析,接近螺旋形曲杆的缠绕数等于其缠绕的匝数减去1 [4]。观察流动环的状态1,钢带共缠绕15匝,无扭转现象。其缠绕数$W_{\rm r} = 15- 1 = 14$,扭转数$T_{\rm w} = 0$。根据White公式,连接数$L_{\rm k} = 14 + 0 = 14$。状态2的匝数减为14,$W_{\rm r} = 14 - 1 = 13$,连接数$L_{\rm k} = 14$保持不变,扭转数$T_{\rm w} = 14 - 13 = 1$。 表明状态2 扭转了1 圈,扭角为$2\pi$。

近似将流动环视为多个圆环的组合。状态1视为15个半径为$R_1$的无扭转圆环。设钢片的弹性模量为$E$,截面的二次矩为$I$,其弯曲变形势能$V_1$为

其中$a,b$为钢片截面的宽度和厚度。当流动环由状态1张开为状态2时,转变为14个半径为$R_2$的圆环的组合,其弯曲变形势能${V}'_2$为

由于状态2存在扭率,还需补充扭转变形势能${V}''_2$。设钢片的切变模量为$G$,截面的二次极矩为$I_0$,钢片的总长度为$L$,得到

其中$\kappa = 0.285$为截面形状因数。状态2的总变形势能$V_2 = {V}'_2 +{V}''_2$。

将量测得到的数据$R_1 = 58.4$ mm,$R_2 = 62.5$ mm,$a =3$ mm,$b = 0.68$ mm和钢材的材料常数$E =210$ GPa, $G = 80.7$ GPa代入计算,得到两种状态的变形势能

$$ V_1 = 29 \text{J}, V_2 = 25 \text{J} $$

$V_2 < V_1$,证实状态2的势能小于状态1,从而使形态突变现象的最小势能原理解释有了更确切的依据。图3为流动环势能的定性变化曲线。状态1受扰后以能量稍高的不稳定状态为过渡,向势能最小的状态2演变。弹性势能的减量$V_1 - V_2$源于内应力所做的负功。反之,对状态2的流动环施加扭矩以输入能量,也能恢复为状态1。流动环在合拢和张开之间可重复变形。

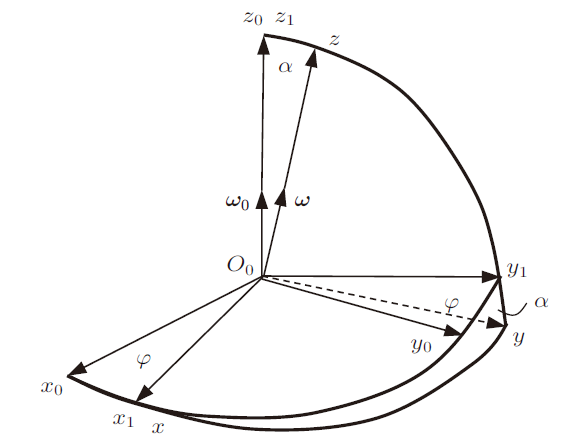
将状态1的流动环套在手臂上转换为状态2,即在重力作用下沿手臂自由下落。为便于分析,将手臂简化为竖直的圆柱体。将流动环简化为多个相同的独立圆环,但在下落过程中保持流动环的整体形态不变,作刚体的平动和转动。以单个圆环为分析对象。当流动环紧贴手臂下落时,观察到圆环与手臂有一个接触点,记作$P$。设由于摩擦的约束作用,圆环在$P$点处相对圆柱体做纯滚动。设垂直的圆柱体对称轴为$z_0$,以圆环的环心$O$至接触点$P$的连线$OP$与$z_0 $轴的交点$O_0$为原点,建立平动参考系$\left( {O_0 \text-x_0 y_0 z_0 } \right)$,$\left( {x_0y_0 } \right)$沿水平面。设$\left( {O_0 \text- x_0 y_0 z_0 } \right)$绕$z_0$轴转过$\varphi $角的位置为$\left( {O_0 \text- x_1 y_1 z_1 } \right)$,其中$x_1$轴沿坐标面$\left( {x_0 y_0 }\right)$与圆环平面相交的节线。为简化分析过程,设$x_1$轴指向与圆环的接触点$P$。同在此节线上的圆环中心$O$与$O_0$, $P$共线。将$\left( {O_0\text-x_1 y_1 z_1 } \right)$的原点移至$O$ 点,令$\left({O \text-x_1 y_1 z_1 } \right)$绕$x_1 $轴顺时针转过$\alpha $ 角后的位置为$\left({O \text- xyz} \right)$,$\left( {x,y} \right)$为圆环平面,$\alpha$为圆环平面相对水平面的倾斜角。$z$轴为圆环平面的法线(图4)。

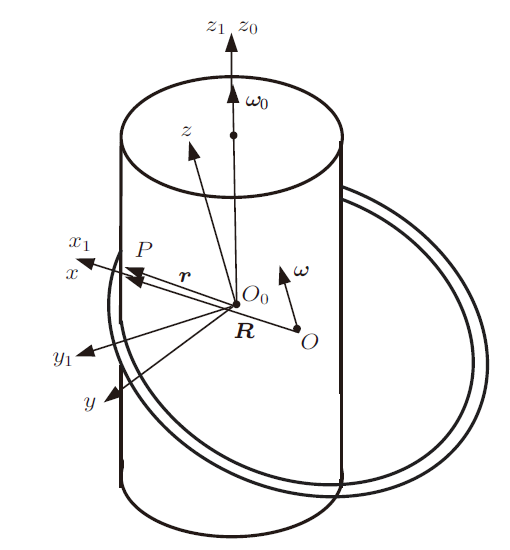
根据观测,在流动环的运动过程中,圆环仅绕$z$轴滚动,绕$x$和$y$轴无转动。圆环平面$\left({x,y} \right)$相对动坐标系$\left( {O_0\text- x_1 y_1 z_1 }\right)$的方位保持不变。以$ i, j, k$表示坐标轴$x,y,z$的基矢量,圆环以角速度$ \omega= \omega k$ 在$P$点处朝$y$轴方向相对圆柱体作无滑动的纯滚动(图5)。定义矢量$ R = \overrightarrow {OP} = R i$,环心$O$的速度为

列出圆环质心运动的动力学方程

其中$ F_0$为圆环在$P$点处作用的摩擦力。将式(6)沿垂直轴方向投影,将式(5)代入,设$ f = { F_0}/m$为摩擦力引起圆环沿垂直轴的负加速度,导出圆环的角加速度

随着圆环的滚动,接触点$P$沿圆柱体表面以速度$\omega R$朝$y$轴方向移动,导致$\left( {O \text- x_1 y_1 z_1 } \right)$绕圆柱体对称轴$z_0$以角速度$ \omega _0 = \dot {\varphi } k_0 $转动。定义矢量$ r = \overrightarrow {O_0 P} = r i$,$P$点的移动速度为$ \omega _0 \times r = \omega R j$。利用此条件导出

令上式对$t$求导,将式(7)代入,得到流动环绕圆柱体旋转的角加速度

以$\left( {O\text-xyz}\right)$为参考系,列写圆环相对动点$P$的动量矩定理。考虑实际流动环的圆环之间存在相互联结的牵拉作用,增加用$ M_0$表示的相邻圆环的牵拉力矩,且考虑矩心$P$沿圆柱体表面移动引起的附加项 [5],列出

其中波浪号表示对$\left( {O \text-xyz} \right)$的局部导数。方程(10)对$\left( {O \text-xyz} \right)$各轴的投影式均能借助待定的$ M_0$得到满足。以沿$z$轴的投影式为例

上式右边第一项为负值,表明扣除阻力的重力$m( g- f)$虽能使圆环的质心运动加速,却对圆环的转动起制动作用。如没有足够强大的$M_{0z}$存在,式(7)确定的角加速度$\dot {\omega}$不可能满足欧拉方程(11),圆环的滚动也不可能实现。由此可见,圆环之间的牵拉力矩$ M_0$对流动环的加速旋转起着不可忽视的重要作用。将圆环对$P$点的惯量矩$J_z = 2mR^2$,目测的倾斜角$\alpha = 30^\circ$和式(7)代入式(11)计算,与重力对$P$点的力矩$ - 0.5mR( {g - f})$相比,牵拉力矩$M_{0z} = 3mR({g - f})$为重力矩的6倍。

将流动环套在半径$r =0.04$ m的垂直圆筒上作下落实验,用秒表量测下落时间。共量测21次取平均值。测出下落至距离$h= 0.76$ m的时间为$t_0 = 1.78$ s。流动环在此期间转动了$n = 6$圈。此过程的加速度为$g - f = {2h}/{t_0^2} = 0.48$ m/s$^2$,角加速度为$\dot{\omega}_0 = {2n}/{t_0^2} =23.86 {\rm rad/s^2} =3.8$ \text{圈}/s$^2$,末角速度$\omega _0 = \dot {\omega }_0 t_0$为每秒$6.7$ 圈。将目测的倾斜角$\alpha = 30^\circ$和其他数据代入式(9),计算得到$\dot {\omega }_0 = 20.85 rad/s^2 = 3.3$ 圈/$s^2$,末角速度$\omega _0 = \dot{\omega }_0 t_0$为每秒5.9圈。理论分析结果与实测数据吻合较好。

本文分析了流动环的几何形态突变,以及绕圆柱下落旋转两种现象的动力学过程。将流动环视为由多个相同圆环组成的形体。实际计算了流动环在合拢和张开两种状态下的应变能,验证了流动环由合拢状态向张开状态的突变是最小势能原理的具体体现。

在分析流动环绕手臂的下落运动时,除重力和摩擦力以外,增加邻近圆环的牵拉力矩以体现各圆环之间的相互联系。分析表明,流动环下落时产生旋转的原因是由于与手臂接触点的约束迫使圆环朝斜下方作纯滚动。滚动过程中环心的周向速度导致流动环绕手臂旋转。数值计算结果与实验量测值较好吻合。从而对流动环的两种特异现象给出合理的动力学解释。