第24届冬季奥运会于2022年2月4日在北京盛大开幕,这一万众瞩目的冰雪盛会再一次使中国成为全球焦点,向世界展示了我国人民的民族文化自信以及国家的经济和科技实力。在冬奥比赛项目中,短道速滑项目向来是中国队的夺金热门,截止至2018年平昌冬奥会,中国已获得的13枚冬奥金牌中有10枚出自短道速滑项目。中国女运动员杨扬获得过59个短道速滑的世界冠军,王濛曾10次打破世界记录。中国男运动员武大靖在2018年平昌冬奥会上获得男子500 m短道速滑金牌^[1],也是我国在该届冬奥会上唯一的金牌。而2022北京冬奥会中,我国运动健儿在短道速滑混合2000 m接力和短道速滑男子1000 m比赛中取得了金牌^[2]。

短道速滑的比赛规则很简单,运动员们于同一起跑线蹬冰起跑,过程中进行追逐超越,最后以冰刀通过终点的先后顺序论胜负。短道速滑的比赛场地很小,跑道为椭圆形,内缘周长为111.12 m,其中直道长28.85 m,弯道最小半径只有8 m。赛道短,意味着更多的弯道和更急的转弯,可以说弯道就是追逐超越、考验战术和技术的重要区域,胜负往往就决定于这瞬息万变的弯道竞速过程之中^[3]。

短道速滑选手在弯道高速滑行的过程中双腿弯曲,身体向左侧大幅度倾斜,伸出去的左手可以接触到冰面。这个动作在静止状态下是无法完成的,而运动员在赛场上不但可以做到,而且可以实现在过弯时超越对手。同时在比赛中也经常可以看到,有运动员在弯道超越的过程中在没有受到外力干扰的环境下仍然可能在过弯时摔倒并滑出赛道。在观看短道速滑比赛时观众一般会产生以下的疑问：短道速滑运动员高速过弯时为什么要大幅倾斜身体而又能保持平衡不倒的;有什么原因会造成他们摔倒呢;他们摔倒之后为什么都无一例外地滑出圈外?而这些问题的答案是与短道速滑比赛背后的运动学和动力学过程紧密相关的。

本文主要借助高中物理以及大学工科专业理论力学的基本知识,通过对短道速滑运动员高速过弯时的运动学描述以及动力学分析来对短道速滑运动员大幅度倾斜身体过弯的力学原理进行解释。通过牛顿第一、第二定律以及实验观测来获得质点做匀速圆周运动时向心加速度的计算公式。借助动力学理论中的达朗贝尔原理^[4-6]在与运动员随动的非惯性系统中引入惯性力,通过力系平衡分析来探究运动员过弯时大幅度倾斜身体的必要性,并给出运动员过弯时身体倾角的计算公式。借助模拟赛道实验来验证相关的分析结论。通过讨论短道速滑运动员在比赛中根据预定战术和现场比赛情况随时变化的线速度以及内外赛道的切换需要来分析运动员在过弯时的各类运动学参数的变化,给出影响运动员高速过弯的关键因素。

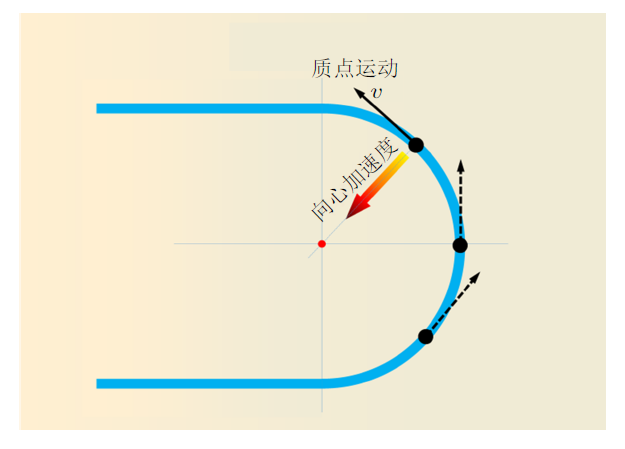
短道速滑运动员在比赛过程中的运动轨迹包括直道加速、入弯、弯道滑行、出弯这四个阶段。建立一个理想化的运动员运动模型,将弯道滑行中的运动员想象成一个只具有质量但忽略身高、体型的理想化质点,想象运动员在弯道滑行过程中的每一个瞬间都是在围绕某个圆心做圆弧运动(如图1所示)。根据牛顿第一定律可知：在平衡力系作用下一个质点只可能保持静止或者做匀速直线运动。如果某一时刻质点在弯道上做匀速直线运动,那么在下一时刻质点就会冲出赛道。

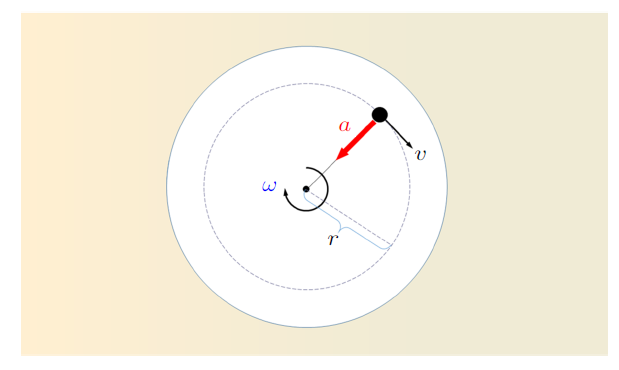
而事实上运动员在弯道上的任意时刻都保持围绕某一圆心做弧线运动的过程,即便它的线速度大小没有改变,是匀速率运动,但它的速度方向却一直在变化。因此质点并非在平衡力作用下进行运动,它拥有一个指向圆心的加速度。这个加速度时刻调整着运动员质点的行进轨迹,使它保持圆弧运动而不是直线运动。这个加速度即为向心加速度。为了能保持圆弧运动,质点必须时时刻刻拥有这一指向圆心的向心加速度。根据牛顿第二定律可知：只有对质点施加外力才能使其产生加速度,因此,若要质点拥有向心加速度从而保持圆弧运动,就必须有外力作用于该质点。图2所示为质点做匀速圆周运动的示意图。其中$r$为质点圆周运动半径,$v$为线速度,$\omega$ 为角速度,$a$为向心加速度。

做匀速圆周运动质点的向心加速度大小的计算公式为

式(1)给出的是向心加速度与角速度以及运动半径间的数值关系,而运动员在比赛过程中可以控制的是其线速度$v$。根据角速度与线速度换算关系$\omega=v/r$,我们进一步给出向心加速度与线速度的数值关系

产生向心加速度所需外力$F$的大小根据牛顿第二定律计算获得

其中$m$为质点总质量。

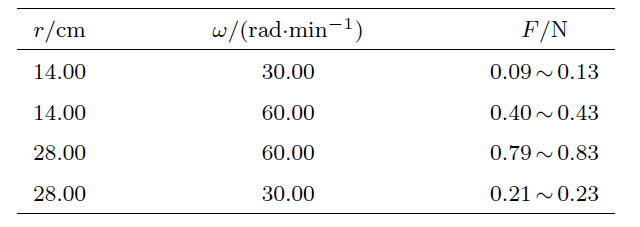
本小节通过质点匀速圆周运动实验来验证1.1节中关于向心加速度的相关计算公式。如图3所示,选取一个半径为30 cm的光滑圆形玻璃平台,其表面较低的摩擦系数可确保在水平方向上的摩擦力足够低。在玻璃平台的中心位置开有一个小孔,电机的转动轴从小孔探出,其转速可控。电机转动轴通过3D打印的塑料板与一个数字拉力计牢固粘结,可以带动拉力计一起同步转动,该数字拉力计可将自身所承受的拉力进行实时显示,通过细绳将一开孔钢珠与数字拉力计连接。钢珠直径为1.5 cm,质量为0.065 kg。细绳的重力可忽略不计,细绳所承受的作用力将通过拉力计实时测量并显示出来,在自由状态下拉力计示数为0 N。同时,在实验平台边缘设置有一个光学转速计,用以实时测量钢珠的转动角速度。实验中将选取不同的控制参数(圆心到钢珠的距离、钢珠的转动角速度)并测量记录细绳所提供的拉力值,实验参数和测量结果在表1中列出。

表1中所列出的测量结果验证了1.1节中关于质点做匀速圆周运动的数学描述,即质点的向心加速度与其角速度平方、运动半径分别成正比关系;或向心加速度与线速度平方成正比而同时与运动半径成反比。运动员在弯道滑行时就必须具有向心加速度,运动员的转弯线速度越大其所需的向心加速度就会成平方倍地增加,而在行进线速度不变的条件下,内道的转弯半径较小,那么运动员需要更大的向心加速度;外道的转弯半径较大,因此运动员需要较小的向心加速度。由此可见,运动员弯道滑行过程中每一时刻所需的加速度大小依赖于当时的线速度大小以及所选择的赛道。

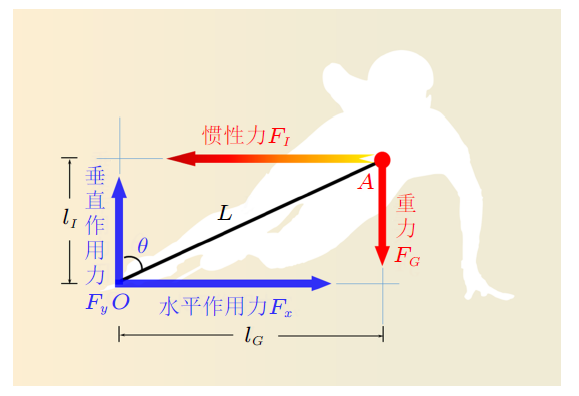
图4所示为运动员在弯道滑行某一时刻的姿态示意图,我们将参考系固定在运动员身上并与之随动。在本节中需要对运动员过弯时的身体姿态进行分析,因此不能再将运动员作为理想化质点来考虑。此刻在图4所示的平面内,运动员受到两类外部作用力。首先是作用在运动员质心$A$点且方向垂直向下的重力$F_{G}$。其次,在冰面与冰刀的接触点$O$处,冰面通过冰刀对运动员施加一个垂直向上的作用力$F_{y}$ (大小等于运动员所受重力)以及一个水平向右的作用力$F_{x}$。这个水平作用力提供给运动员向心加速度使其做圆弧运动,其作用等同于1.2节实验中细绳对钢珠施加的拉力,方向指向运动员做圆弧运动的圆心方向。运动员左手与冰面接触是为了自我保护,左手承受的外力可忽略不计。以上为图4所示的平面内运动员所受主要外力。

本文所选取的参考系与运动员随动,属于非惯性系统。为了能够在这一系统中开展静力学平衡分析,需要根据动力学理论中的达朗贝尔原理^[4-6]在这一非惯性系统中引入一个惯性力$F_{I}$。该惯性力的大小与冰面提供的水平作用力$F_{x}$相等,作用于运动员质心$A$点,方向与冰面水平作用力相反,如图5所示。

为了保持图5所示平面内的力系平衡,系统中的合力以及合力矩应当为零。合力为零要求

选择冰刀与冰面的接触点$O$为参考点,力系合力矩为零要求重力$F_{G}$与惯性力$F_{I}$关于$O$点的力矩大小相等

式中,$l_{G}$和$l_{I}$分别为重力和惯性力关于$O$点力矩的力臂长度,它们的大小可表示为

式中$\theta$为运动员身体关于竖直方向的倾角,$L$为线段$OA$的长度。从而可导出运动员身体倾角的表达式为

式中$g$为重力加速度,大小为9.8 N/kg。

如果此刻过弯的选手没有倾斜身体,而是保持身体与冰面垂直,那么此时由于重力通过参考点$O$,它的力臂为零,产生的力矩也为零。而惯性力产生的力矩却不为零,因此运动员无法保持现有姿态,将在惯性力产生的力矩作用下翻出赛道。如果运动员身体有足够大倾角的话,重力的力臂就不再为零,此时重力与惯性力所产生的力矩就有可能相互抵消,在平衡力系作用下运动员就可以维持其当前姿态。

由式(7)可知,短道速滑运动员过弯时的倾角只依赖于其该时刻的向心加速度,而从式(2)可知,运动员过弯时向心加速度的大小分别与滑行速度平方成正比,与转弯半径成反比。因此运动员滑行的速度提高或者选择弯道半径较小的内道过弯时,需要更高的向心加速度,那么相伴随的就是更高的惯性力,这时候运动员就需要做出更大的倾斜角来实现平衡。而由于运动员在弯道滑行过程中,其线速度和运动轨道半径都不会是一成不变的,所以运动员需要不断调整自己的倾角以保持运动平衡。一般来说,运动员在弯道超越或做战术配合的时候需要随时改变运动半径或线速度,为了保持身体平衡就必须及时调整身体倾角,一旦倾角调整不及时就会失去平衡摔出赛道。

我们采用电动小跑车带着人形木偶在赛道上行驶来模拟运动员进行的弯道滑行过程(图6)。实验中模拟赛道的宽度为16 cm,其中直道总长度为32 cm,转弯半径为20 cm。实验中准备了两辆相同规格的小跑车,车顶固定了相同的人形木偶。其中一个是笔直站立姿态,另一个是屈膝身体倾斜约40$^\circ$,模拟运动员过弯时的体态。把两辆带着不同姿态人偶的小跑车放置在同一条跑道上,通过控制器给跑车供电,让它们以同样的速度在跑道上行驶。在实验中观测到,在弯道赛段,搭载笔直站立人偶的小跑车刚一进入弯道就翻出了赛道,而保持短道速滑运动员过弯姿态的人偶所乘的这辆小跑车却没有出现问题,表现出较高且稳定的过弯能力。

根据式(7)可知,运动员所需身体倾角依赖于其过弯时的加速度,而加速度与运动员线速度平方成正比。因此在随后的实验中,我们施加了更高的线速度来考察带有40$^\circ$倾角的人偶跑车的过弯能力。观察到当线速度进一步提升后,由于没有对人偶进行相应的倾角调整,人偶小车在弯道失去平衡而滑出赛道。

通过前述理论分析和实验再现,本文阐明了短道速滑运动员在弯道保持弧线运动状态的先决条件是需要外力为其提供向心加速度,一旦失去这个向心加速度(比如摔倒),运动员的运动状态将从弧线运动转为直线运动从而摔出圈外。运动员在弯道滑行过程中是通过冰面对冰刀产生的水平作用力来提供这一向心加速度的,而在弯道大幅度倾斜身体是为了实现力矩平衡,从而保持当前运动姿态的稳定。运动员必须时刻调整合理的倾角范围,来配合他们根据预定战术和现场赛况不断改变的滑行速度与转弯半径,实现在平衡中抢位超越。因此弯道大幅倾斜身体滑行是运动员必备的技能,也是取胜的关键,可以说弯道技术的优劣会直接影响到比赛的最终成绩。