2022年2月4日,第二十四届冬季奥林匹克运动会在北京拉开帷幕,冬奥会作为全世界最为瞩目的冰雪赛事,受到全世界各国人民的关注。在所有冬奥会项目中,不得不提到一个运动——冰球。冰球,也被称为"冰上曲棍球",是冬奥会中唯一的集体球类项目,在1924年第一届冬季奥运会中被列为正式的比赛项目。冰球比赛中运动员穿上护具和冰刀,在光滑的冰面上高速滑行,并运用冰球杆作为工具通过推、拨、盘、带等各种动作来控制冰球。冰球队员们需要相互配合,协调作战,其目标只有一个,就是射门、进球、赢得比赛,因此快速精准的射门技术是至关重要的。大力击射是冰球比赛中常用的一种射门技术,运动员通过身体腰腹力量以及快速转体,将冰球杆举高,快速击打冰球使其具有非常高的速度,完成冰球的射门。那么,冰球大力击射背后的力学原理是什么呢?下面我们将从冰球大力击射模拟实验和理论力学的角度,揭示为什么通过大力击射可以打出具有高速运动的冰球。

冰球运动员大力击射时,冰球移动的速度非常快,其最高时速可达到170 km/h。那么怎样才能打出这么高速运动的冰球呢?冰球在冰面滑动过程中的摩擦阻力和冰球在空中飞行过程中的空气阻力,对于冰球移动速度有些许影响,但并不明显,冰球的速度主要是由运动员击打动作决定的。在大力击射过程中,首先,运动员将放在下端的手握在球杆的中央部分并握紧球杆。同时双腿微微弯曲,后腿向后蹬,让自己进入击球的状态。其次,选择适当时机,转动上半身和手腕,协调来自腿部、肩膀、手臂的核心肌肉,获得力量,从而快速击球。在整个过程中,击球之前的蓄力成为高球速的关键。最重要的是,运动员在蓄力准备击球的时候,根据球的位置、专注于上半身转动这个动作,而后通过回旋击球。为了探究击球前身体转动对冰球击出速度的影响,下面通过设计的冰球大力击射模拟实验来揭示其中的奥秘。

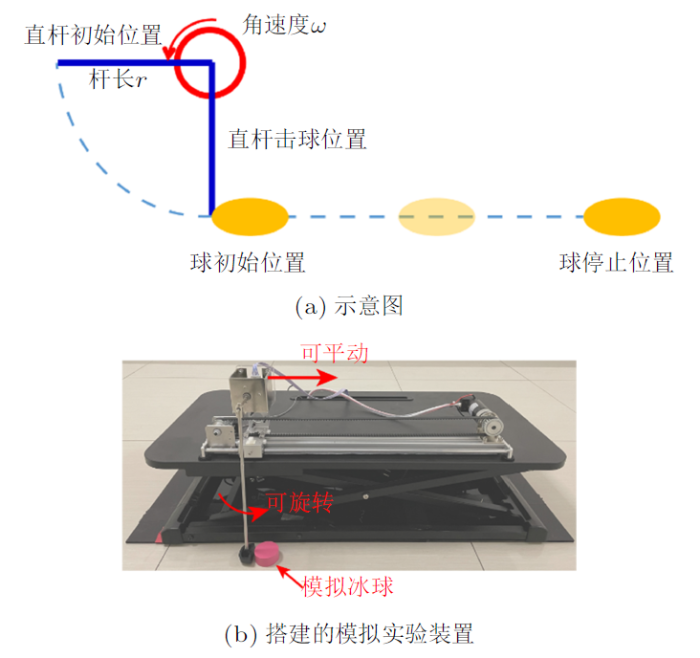
首先,我们将冰球运动员简化成一个可以转动的刚性圆柱,将冰球杆简化成细长直杆,将冰球简化成一个小圆盘,冰球大力击射实验的设计示意图如图1(a)所示。根据图1(a)来搭建模拟实验的装置,主要包括一个平动滑行装置(功率55 W)、一台可产生旋转运动的电动机(功率4.5 W)、金属直杆(直径0.8 cm,长度可调节为30 cm/35 cm/40 cm)、模拟冰球的圆盘形物体(直径3.5 cm,$\times$,高1.5 cm)。在模拟实验中,利用平动装置可以模拟运动员的水平滑动,同时放置于桌面上的可产生旋转运动的电动机连着金属直杆,电动机带动金属直杆,以一定的角速度打击圆盘形物体,使圆盘形物体在放置于地面上的光滑塑料板上运动,搭建的模拟实验装置如图1(b)所示。

下面我们将通过模拟实验得到的数据,分析直杆的旋转角速度$\omega$和直杆的长度$r$对圆盘形物体速度的影响。为便于观察,我们以每次击球后圆盘形物体的滑行距离$l$来量化其击出速度,对于每组参数均完成3次实验,并取其平均值。

固定直杆的长度$r=30$ cm,让电动机产生不同的旋转角速度$\omega$。通过实验数据表1可见,当不允许直杆转动只滑动时,即$\omega=0$时,通过3次实验测得圆盘形物体的平均滑行距离为19 cm。在旋转角速度$\omega =3.6$ rad/s时,通过3次实验测得圆盘形物体的平均滑行距离是45 cm;当旋转角速度$\omega $增大到4.8 rad/s时,重复刚才的实验,圆盘形物体的平均滑行距离是61 cm;进一步增加旋转角速度$\omega $到6.0 rad/s时,通过3次实验测得圆盘形物体的平均滑行距离为89 cm！显见,随着旋转角速度$\omega $的增加,圆盘形物体的平均滑行距离也大大增加。因此,要想获得更大的冰球速度,需要我们在击球前有更大的身体转动速度,这也解释了为什么大力击射时运动员需要快速转体。

固定直杆的旋转角速度$\omega =3.6$ rad/s,直杆的长度$r$分别取30 cm,35 cm和40 cm。通过实验数据表2可见,当$r=30$ cm时,通过3次实验测得圆盘形物体的平均滑行距离为45 cm;当$r=35$ cm时,通过3次实验测得圆盘形物体的平均滑行距离为50 cm;当$r=40$ cm时,圆盘形物体的滑行距离的3次平均值为67 cm。显见,随着直杆的长度$r$增加,圆盘形物体的平均滑行距离也在增加。因此,在冰球大力击射时,保持身体与球之间的适当距离,果断击球,才能获得更好的射门效果。

本节主要根据理论力学的知识,揭示上述冰球大力击射模拟实验结果背后的力学原理。

假设质点的质量为$m$,其绕定轴旋转时的角动量定义为^[1]

其中$p=mv$为质点在垂直于轴的平面内的动量,$r$为质点到旋转轴的距离,$v$为质点的速度,具体见图2(a)。如果对应到第1节中的模拟实验装置,根据图2(b),圆盘形物体的质量为$m$,直杆的杆长是$r$,当圆盘形物体被击射出之后,它的速度为$v$,那么它关于旋转轴的角动量仍可以由式(1)表达。

另外,根据理论力学的知识可知,对于一个绕定轴旋转的质点$m$来讲,角动量$L$还可以定义为^[1]

其中$\omega$是转动角速度,$I$为转动惯量。同样,如果对应到冰球大力射击模拟实验中,根据图2(b)和图3,$\omega$是由旋转电机控制的旋转角速度,如果以冰球运动员上半身为转轴,运动员简化为一个转动的刚性圆柱,假设圆柱体的质量为$M$,半径为$R$,则其转动惯量$I=MR^2/2$。

在冰球大力击射过程中,通常将运动员、球杆、冰球看成一个整体。认为运动员击打冰球前后的角动量保持不变,也就是说运动员将一部分角动量转移给了冰球,变成了冰球的动量矩,也就使得冰球获得了移动速度。根据式(1)和式(2),可写出冰球大力击射中的角动量守恒方程

其中$I$为运动员的转动惯量,$\omega_{1}$和$\omega_{2}$分别为运动员击球前和击球后的角速度,$v$为冰球击出速度。

另外,在弹性碰撞的假设下,系统的总动能是守恒的,即击打冰球前快速转动的运动员的动能等于击打之后冰球的动能和运动员的动能之和,故冰球大力击射中的能量守恒方程为

利用方程(3)和(4)可得击射出的冰球的最终速度为^[2]

由式(5)可以看出,冰球的最终速度$v$ 与运动员击球前的旋转角速度$\omega_{1}$成正比。即冰球运动员击球时,旋转角速度$\omega_{1}$越大,击射出的冰球获得的最终速度$v$就越大,故冰球射门速度越快,与冰球大力击射模拟实验得到的表1中的数据分析结果一致。换言之,运动员身体转动的速度和击打时机对于冰球最终速度来说是关键因素,这也解释了冰球大力击射时运动员需要快速转体的力学原理。此外,由于运动员的体重要比冰球的质量大得多,故$I=MR^2/2$很大,即$I\gg mr^{2}$,则式(5)可近似估计为$v\approx 2r\omega_{1}$,说明冰球距离转轴的距离越大,击打出的冰球速度也越大,与冰球大力击射模拟实验得到的表2中的数据分析结果一致,揭示了冰球大力击射时,运动员必须保持身体与球之间的适当距离才能获得更好的射门效果的力学原理。

冰球运动是以冰刀和冰球杆为工具在冰上进行的一种相互对抗的集体性竞技运动,强调团队作战,目的是通过大力击射、进球、取得比赛的胜利。本文通过理论力学的基本知识和冰球大力击射模拟实验,解释了冰球大力击射技术背后的力学原理。通过理论力学和实验数据分析发现,冰球的最终速度与运动员击球前的旋转角速度成正比,解释了为什么运动员在击球前需要更大的身体转动速度来获得更大的冰球速度。同时,从力学的角度来讲,冰球距离转轴的距离越大,击打出的冰球速度也越大,但是在实际的冰球比赛中,并不是距离转轴的距离越大越好,而是存在一个最佳的距离,因此,在运动员进行大力击射时,需要保持身体与球之间的适当距离,果断击球,才能获得更好的射门效果。

本文的目的是希望将力学理论知识与实验工作与冬季奥运会运动相结合,推动科技体育,为冰雪运动的普及做贡献。