空间维护原理是我校运筹与任务规划专业本科学员的一门核心主干课程,讲述内容包括航天器轨道动力学和机械臂动力学,航天器轨道动力学又包括远程轨道机动动力学和近程轨道机动动力学,是航天领域的一门基础学科,对于培养航天专业人才具有重要意义[1 -3 ] 。远程轨道机动需要用到绝对运动动力学模型,它是在惯性坐标系中建立的,用于描述航天器的绝对动力学特性;相对运动动力学模型是在目标轨道坐标系中建立的,用来描述追踪星相对目标星的动力学特性。航天器的相对运动类型包括交会对接、绕飞、跟飞、掠飞、悬停、编队飞行等。多个航天器相对运动轨迹具有瞬时变化和长期演化的特性,且在不同的参考坐标系中具有不同的形状,相对运动规律与地面的相对运动规律往往在直觉上是相悖的,对学员的空间想象力提出了较高的挑战。在授课过程中,学员难免会感到抽象乏味,难以将离散、抽象的数学公式与实际中的物理运动建立联系,普遍存在畏难情绪[4 ] 。
课程组借用信息化手段,同步开设了空间维护原理线上课程,探索翻转课堂、线上线下相结合的混合式教学模式,满足学员的个性化学习需求。重视基于板书、MATLAB和GeoGebra的公式推导,充分体现逐步引导学生学习、引导学生思维的过程。将数学模型中的各物理量与物理模型建立联系,借助成熟STK软件中的三维和二维显示功能以及其他仿真软件[5 -6 ] ,构设虚拟仿真实验环境,展示太空中两个航天器的相对运动过程,通过将抽象的概念具体化帮助学生理解相关的理论。
经过近几年的教学实践,课程组逐步形成了演示法、交互法和实验法三位一体的教学方法,其中,演示法为交互法提供概念支撑,交互法为实验法提供理论依据,实验法为演示法提供数据来源,共同形成一个有机、体系化方法论。明确提出了我们教学思路是注重基础、挖掘深度、强调主干,即注重数学模型基础,注重数学模型和物理模型的关联;深入研究教学内容,挖掘教学内容深度,包括与教学内容相关学科最新进展,修改教材、文献中的不完善、不准确的论述和表述,超越现有教学内容,提升知识广度;强调相对运动和绝对运动的关系,达到融会贯通的目的。下面是课程组在航天器相对运动动力学教学实践中的总结与体会。
1 演示法提供概念支撑
课程组在教学过程中充分利用图形对比、STK的三维和二维显示功能进行相对运动规律的演示、讲解,让抽象的数学模型和物理模型建立对应关系,让静态的公式动起来,从而让学生对相对运动规律建立直观的感受。
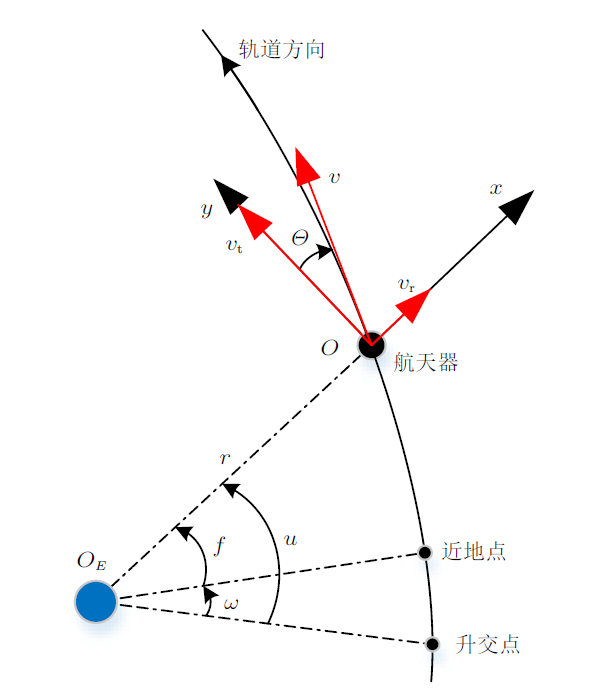
下面围绕航天器相对运动教学中存在的重难点问题进行说明。在相对运动教学中,学员普遍反映的理解难点有三个:第一个是太空中两个航天器,给一个航天器施加制动力,则这个航天器相对于另外一个航天器先向后再向前运动,原因是什么;第二个是绝对运动轨迹和相对运动轨迹有何异同;第三个问题是在描绘相对运动轨迹时,如果右手边为卫星运动方向,则相对运动轨迹都是逆时针的,如果左手边为卫星运动方向,则相对运动轨迹都是顺时针的。
1.1 施加切向脉冲后的相对运动轨迹
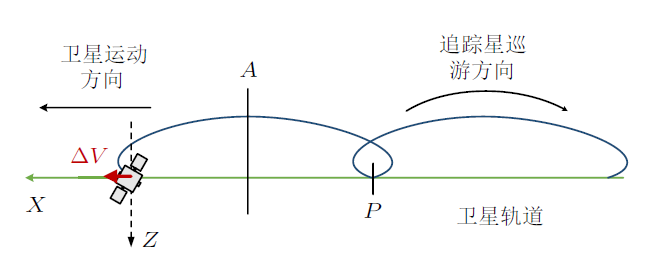
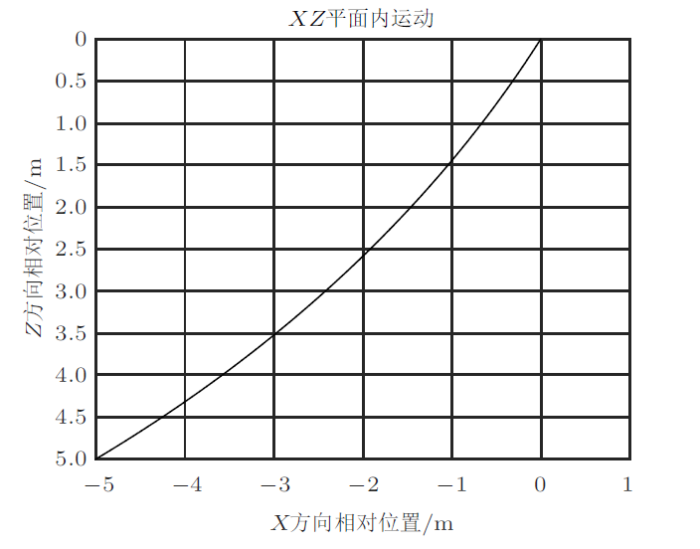
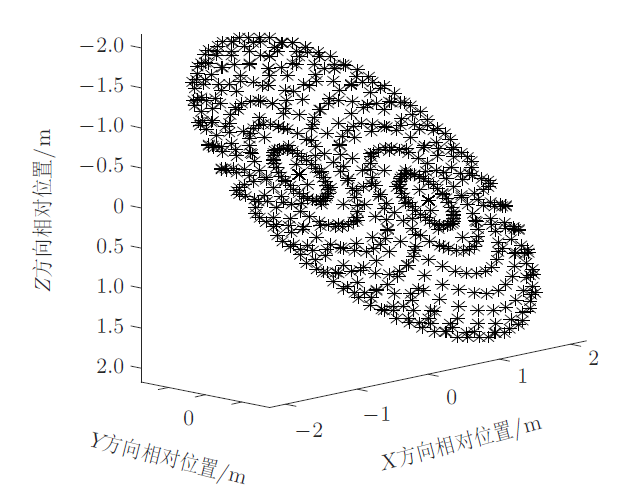
太空中的相对运动规律与地面运动规律不同,典型的一个例子就是施加沿速度方向的脉冲后,相对于原来的位置,卫星先向前再向后运动,而对于地面的汽车如果踩油门加速的话,是向前冲的。总体来看,卫星的轨迹是向后上方运动的,图1 给出了施加推进力作用后卫星相对运动轨迹。这个问题也是开展相对运动教学的"引入问题",通过设问法,引起学员的兴趣,引导学员尽快进入学习状态。
图1
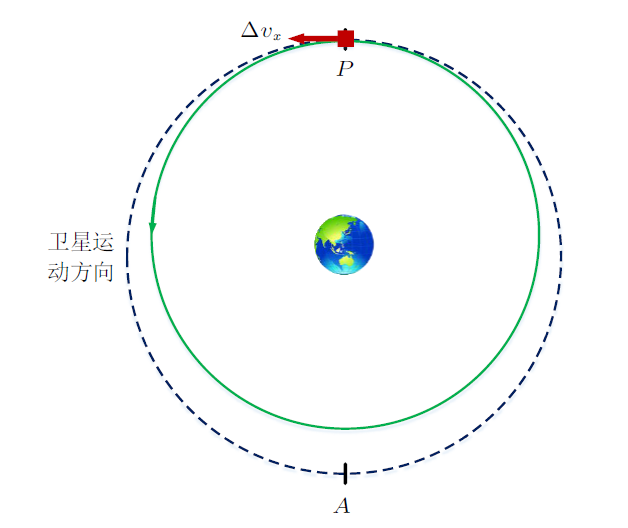
在惯性坐标系下的轨迹如图2 所示,绿色代表原来的轨迹,蓝色虚线代表施加脉冲后的轨迹,$P$表示近地点,$A$表示远地点,半个轨道周期后到达远地点,一个周期后到达近地点,即原轨道高度,与图1 存在一一对应的关系。通过惯性系和目标轨道坐标系下运动轨迹的对比,让学员加深对卫星相对运动的理解。
图2
1.2 绝对运动和相对运动轨迹是如何对应的?
通过前置课程的学习,学员对惯性系下的绝对运动有深刻的认识,因此将相对运动与绝对运动轨迹进行结合,有助于提升教学效率。图2 给出了施加切向脉冲后的绝对运动轨迹。下面结合施加径向脉冲进行扩展说明。
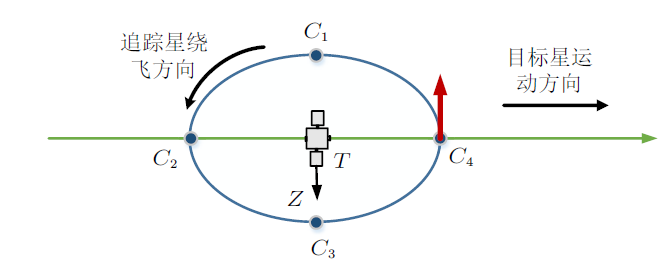
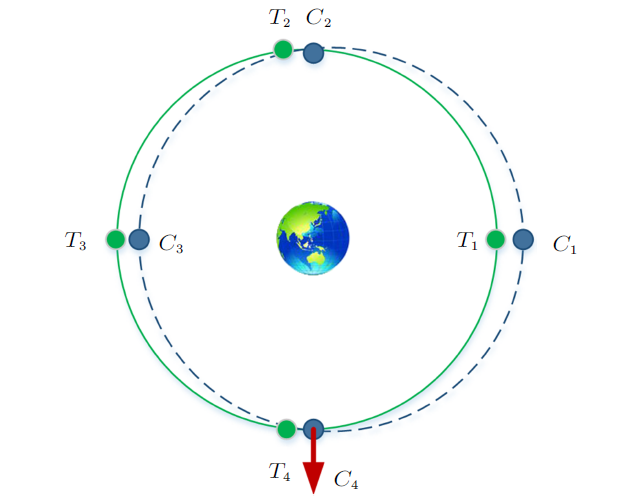
图3 给出了施加径向脉冲后,目标轨道坐标系中的相对运动轨迹,追踪星对目标星实现了绕飞,在图4 中,对应给出了惯性坐标系下的绝对运动轨迹,绿色实线代表目标轨道,蓝色虚线代表追踪星轨迹,不同时刻的位置用下标1~4表示,假设初始时刻追踪星位于目标星前方($T_{4}$和$C_{4}$),施加一次$Z$轴负方向(背离地心方向)的脉冲,则追踪星绕目标形成逆时针的绕飞(图3 ),$C_{1}$时刻追踪星位于目标星上方,$C_{2}$时刻追踪星位于目标星后方,$C_{3}$时刻追踪星位于目标星下方,通过绝对运动和相对运动的比对图,学员更加容易理解惯性坐标系下的绝对运动轨迹。
图3
图4
1.3 逆时针是普遍运动规律还是特殊运动规律
为了更好地说明相对运动轨迹的运动趋势,可以选择成熟的STK软件进行演示分析。图5 中给了VVLH坐标系(黄色坐标系)下的相对运动轨迹,运动方向与$X$轴重合,指向右手侧。每隔45$^\circ$施加一次脉冲,共有8种情况,图5 给出了8条相对运动轨迹,可以看出,相对运动方向都是逆时针的。
图5
同样,如果改变坐标轴的指向,左手边为卫星运动方向,则相对运动轨迹都是顺时针的。通过动画的展示,让学员直观地认识相对运动的规律,熟悉施加不同方向脉冲后的轨迹特点。并且可以观察施加径向脉冲和切向脉冲后相对运动轨迹的不同。
2 交互法提供理论依据
正如冯 $\cdot$ 卡门所说,"自然界具有数学本质"。学员可以通过图形、动画来直观地认识相对运动规律,但要精确地描述相对运动,需要通过相对运动模型、数学模型来分析其物理运动规律,演示描述法或定性方法可以用来研究自然现象,但通过定量方法进行教学可以加深认知,澄清现象的本质。在教学过程中,学员通过演示法了解了航天器的相对运动规律后,往往都有兴趣去探究自然现象背后的原因,所以从实际问题中引出概念,吸引学生参与到数学分析和公式推导过程中来,在推导过程中注重与学员的交互,引导学员去解释相对运动的规律,即"交互法"。
绝对动力学模型一般采用数值解法,可用来精确分析航天器的动力学特性。相对运动动力学模型中应用最广泛的是Clohessy-Wiltshire (CW)方程[7 ] ,它具有简单的线性常系数形式,可用来直观分析相对运动的动力学特性,需要结合推导过程提醒学员的是,CW方程成立的假设是目标运行在原轨道,相对距离较近且忽略了高阶摄动力。
2.1 施加切向脉冲后的相对运动方程
以1.1节施加切向脉冲后的相对运动轨迹为例进行说明。已知CW方程的解析解是
(1) $ \left.\begin{array}{c}x(t)=x_{0}+2 \frac{\dot{z}_{0}}{\omega}-\left(3 \dot{x}_{0}-6 \omega z_{0}\right) t+ \\2\left(2 \frac{\dot{x}_{0}}{\omega}-3 z_{0}\right) \sin (\omega t)-2\left(\frac{\dot{z}_{0}}{\omega}\right) \cos (\omega t) \\y(t)=\frac{\dot{y}_{0}}{\omega} \sin (\omega t)+y_{0} \cos (\omega t) \\z(t)=4 z_{0}-2 \frac{\dot{x}_{0}}{\omega}+\left(2 \frac{\dot{x}_{0}}{\omega}-3 z_{0}\right) \cos (\omega t)+ \\\left(\frac{\dot{z}_{0}}{\omega}\right) \sin (\omega t)\end{array}\right\} $
对于采用化学推进剂的航天器系统,由于发动机具有一定的推力,发动机所需的推进工作时间,与轨道运行周期相比是短暂的,因此通常视为脉冲变轨方式,即推力脉冲式卫星速度有突变式的增量$\Delta v$,但不引起卫星向径$r$的突变。因此在教学过程中通常假设初始时刻具有切向的相对速度$\dot{x}_{0}$。此时的相对位置$x_{0}=y_{0}=z_{0}=0$,相对速度$\dot{y}_{0}=\dot{z}_{0}=0$,将上述条件代入式(1)中,得到
(2) $ \left.\begin{array}{l}x=4 \frac{\dot{x}_{0}}{\omega} \sin (\omega t)-3 \dot{x}_{0} t \\y=0 \\z=2\left(\frac{\dot{x}_{0}}{\omega} \cos (\omega t)-\frac{\dot{x}_{0}}{\omega}\right)\end{array}\right\} $
从式(2)的第一个等式可以看出,当机动时间$t$较短时,$4{\dot{{x}}_{0}}/{\omega }\sin (\omega t)\approx 4\dot{{x}}_{0} t$,因此$x\approx\dot{{x}}_{0} t>0$,当机动时间$t$较长时,$4{\dot{{x}}_{0}}/{\omega}\sin (\omega t)\ll 3\dot{{x}}_{0}t$,因此$x<0$,呈先正值后负值的规律。同样从式(2)的第三个等式中可以看出,$\cos\omega t<1$,所以$z$永远是负值,因为$Z$轴指向地心,$z$为负值代表始终位于原轨道的上方。因此可以通过公式的推导得出结论:施加速度脉冲(即施加推进力),卫星先向前运动再向后运动。结合式(2)推导的结论,回顾图1 演示的效果,巩固了学员对公式的理解,同时对相对运动背后抽象的理论知识加深了认识。
2.2 施加径向脉冲后的相对运动方程
式(3)给出了描述绝对运动的高斯摄动方程[8 ] ,从第一个和第二个等式中可以看出,当目标轨道偏心率为零时,施加径向方向的小脉冲只会改变轨道的偏心率,不改变轨道半长轴大小。
(3) $ \left.\begin{array}{l}\dot{a}=\frac{2 a^{2}}{\sqrt{\mu p}}\left[e \sin f \cdot a_{\mathrm{r}}+(1+e \cos f) \cdot a_{\mathrm{t}}\right] \\\dot{e}=\frac{r\left[\sin f(1+e \cos f) \cdot a_{\mathrm{r}}+\left(2 \cos f+e+e \cos ^{2} f\right) \cdot a_{\mathrm{t}}\right]}{\sqrt{\mu p}} \\\dot{i}=\frac{r \cos u}{\sqrt{\mu p}} a_{\mathrm{h}} \\\dot{\Omega}=\frac{r \sin u}{\sqrt{\mu p} \sin i} a_{\mathrm{h}} \\\dot{\omega}=\frac{r\left[-\cos f(1+e \cos f) \cdot a_{\mathrm{r}}+\sin f(2+e \cos f) \cdot a_{\mathrm{t}}\right]}{e \sqrt{\mu p}}-\cos i \cdot \dot{\Omega} \\\dot{M}=\frac{(p \cos f-2 r e) \cdot a_{\mathrm{r}}-(p+r) \sin f \cdot a_{\mathrm{t}}}{e \sqrt{\mu a}}+\sqrt{\frac{\mu}{a^{3}}}\end{array}\right\} $
假设CW方程输入的初始状态为0,此时$x_{0}y_{0}z_{0}=0$,如果仅施加$-Z$方向脉冲$\dot{z}_{0}$,则$\dot{x}_{0}$和$\dot{y}_{0}$仍为零,解析解可化简为
(4) $ \left.\begin{array}{l}x=\frac{2 \dot{z}_{0}}{\omega} \cos (\omega t)-2 \frac{\dot{z}_{0}}{\omega} \\y=0 \\z=-\frac{\dot{z}_{0}}{\omega} \sin (\omega t)\end{array}\right\} $
通过对式(4)合并同类项,从相对运动方程中可以推导得到式(5)的表达式,因此相对运动轨迹是椭圆。
(5) $ \frac{\left(x+2 \frac{\dot{z}_{0}}{\omega}\right)^{2}}{\left(\frac{2 \dot{z}_{0}}{\omega}\right)^{2}}+\frac{(z)^{2}}{\left(-\frac{\dot{z}_{0}}{\omega}\right)^{2}}=1 $
观察式(5)可以看出,椭圆的长轴大小等于${2\dot{{z}}_{0}}/{\omega }$,绕飞椭圆的偏心率保持为${\sqrt 3}/{2}$。
在地心坐标系中,连接近地点与远地点的直线称为拱线,施加沿径向的脉冲,如果原轨道偏心率为零,则拱线不旋转。但向外的径向速度分量意味着航天器分离其原轨道,位于原轨道上方,这与图4 中所示相对运动规律是一致的。
由共面轨道改变公式,引入能量比参数$\upsilon $,真近地点角$f$的表达式为
(6) $ v=\frac{r v^{2}}{\mu} $
(7) $ f=\operatorname{atan} 2\left(v \sin \Theta \cos \Theta, v \cos ^{2} \Theta-1\right) $
在图6 中,施加径向脉冲($\varTheta =0^{\circ}$)后的真近点角$f$等于90$^\circ$,这也说明两条轨道的交点是关于地球中心对称的,即图4 中$C_{2}$和$C_{4}$关于地球中心是对称的。
图6
同时,施加径向冲量后,径向速度$v_{\rm r}$、周向速度$v_{\rm t}$表示为$f$的函数
(8) $v_{\mathrm{r}}=v \sin \Theta=\sqrt{\frac{\mu}{p}} e \sin f$
(9) $ v_{\mathrm{t}}=v \cos \Theta=\sqrt{\frac{\mu}{p}}(1+e \cos f) $
(10) $ \dfrac{v_{\rm r} }{v_{\rm t} }=e $
因此施加的径向脉冲越大,绝对运动轨道的偏心率越大,等于径向速度和周向速度的比值。
在讲述相对运动规律时,回顾绝对运动讲述内容,利用公式进行简单地推导,用结论说明问题,有助于学员理解抽象的相对运动概念。
3 实验法提供数据来源
实验法指通过MATLAB编写相对运动程序计算脉冲大小,并输入STK中进行演示,验证分析相对运动轨迹和相对运动规律。
以两脉冲交会对接为例,相对运动方程的解析解可以化简为状态转移矩阵的形式
(11) $\left[\begin{array}{c}x_{\mathrm{t}} \\y_{\mathrm{t}} \\z_{\mathrm{t}} \\\dot{x}_{\mathrm{t}} \\\dot{y}_{\mathrm{t}} \\\dot{z}_{\mathrm{t}}\end{array}\right]=\Phi\left[\begin{array}{c}x_{0} \\y_{0} \\z_{0} \\\dot{x}_{0} \\\dot{y}_{0} \\\dot{z}_{0}\end{array}\right]$
(12) ${X}_{\rm t} ={\varPhi X}_{0}$
(13) $\Phi=\left[\begin{array}{cccccc}1 & 0 & 6(\omega t-\sin (\omega t)) & \frac{4 \sin (\omega t)-3 \omega t}{\omega} & 0 & \frac{2(1-\cos (\omega t))}{\omega} \\0 & \cos (\omega t) & 0 & 0 & \frac{\sin (\omega t)}{\omega} & 0 \\0 & 0 & 4-3 \cos (\omega t) & \frac{2(\cos (\omega t)-1)}{\omega} & 0 & \frac{\sin (\omega t)}{\omega} \\0 & 0 & 6 \omega(1-\cos (\omega t)) & 4 \cos (\omega t)-3 & 0 & 2 \sin (\omega t) \\0 & -\omega \sin (\omega t) & 0 & 0 & \cos (\omega t) & 0 \\0 & 0 & 3 \omega \sin (\omega t) & -2 \sin (\omega t) & 0 & \cos (\omega t)\end{array}\right]$
状态转移矩阵${\varPhi }$可以分为四个模块,式(13)化简为
(14) $\begin{array}{c}\Phi\left(t, t_{0}\right)=\left[\begin{array}{ll}\Phi_{\mathrm{r}}\left(t, t_{0}\right) & \Phi_{\mathrm{v}}\left(t, t_{0}\right)\end{array}\right]= \\{\left[\begin{array}{ll}\Phi_{\mathrm{rr}}\left(t, t_{0}\right) & \Phi_{\mathrm{rv}}\left(t, t_{0}\right) \\\Phi_{\mathrm{vr}}\left(t, t_{0}\right) & \Phi_{\mathrm{vv}}\left(t, t_{0}\right)\end{array}\right]}\end{array}$
将式(14)中四个子矩阵代入式(12),则可以得到简化的相对运动方程
(15) $\left.\begin{array}{l}r(t)=\Phi_{\mathrm{rr}}\left(t, t_{0}\right) r_{0}+\Phi_{\mathrm{rv}}\left(t, t_{0}\right) v_{0} \\v(t)=\Phi_{\mathrm{rr}}\left(t, t_{0}\right) r_{0}+\Phi_{\mathrm{Vv}}\left(t, t_{0}\right) v_{0}\end{array}\right\}$
通过数学变换,可以得到需要施加的两次脉冲的大小$\Delta {v}_{1} $和$\Delta{v}_{2} $。
第一次施加脉冲的大小可以由相对距离的关系推导得到,在式(15)第一个等式中,终端时刻的相对距离为零,即${r}\left( t \right)$等于零,代入可得
(16) ${v}_{0}^{+} =-\left[ {{\varPhi }_{\rm rv} } \right]^{-1}\left[ {{\varPhi}_{\rm rr} } \right]{r}_{0}$
(17) $\Delta {v}_{1} ={v}^{+}(0)-{v}(0)$
(18) ${v}\left( t \right)={\varPhi }_{\rm vr} {r}_{0} +{\varPhi }_{\rm vv} {v}_{0}^{+}$
(19) $\Delta {v}_{2} =-{v}(t)$
通过上述推导得到的式(17)和式(19),可以快速计算得到两脉冲交会需要的燃料
(20) $\Delta v=\left\| {\Delta {v}_{1} } \right\|+\left\| {\Delta {v}_{2}} \right\|$
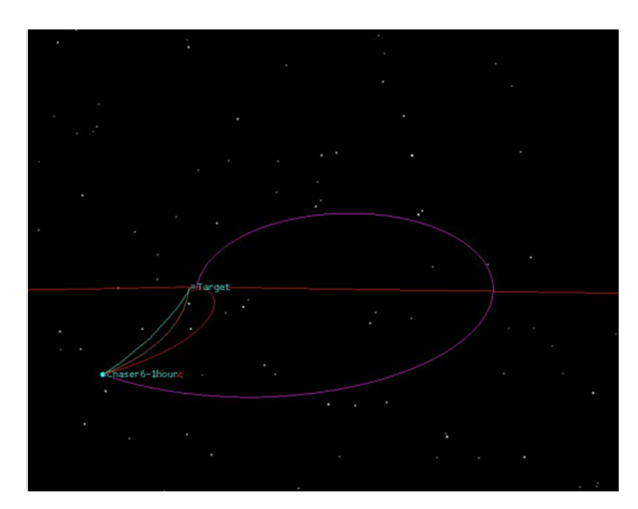
图7 给出了基于MATLAB的1 h接近相对运动轨迹,可以与STK对比验证。通过MATLAB编程计算不同时间交会所需脉冲,将脉冲大小代入到STK的Astrogator模块中,从而得到不同时间接近目标的相对运动轨迹。在图8 中,从左至右,青色轨迹代表1 h接近目标轨迹,黄色代表3 h接近目标轨迹,红色代表1 0 h接近目标轨迹,粉色代表20 h接近目标轨迹。图8 可以启发学生去发现相对运动的规律:第一个规律是交会接近的时间越长,轨迹越缓,消耗的燃料越少;第二个规律是相对运动轨迹都是逆时针的,这与1.3节的结论是一致的,在讲授过程中,学员会有种殊途同归,豁然开朗的学习体验。
图7
图8
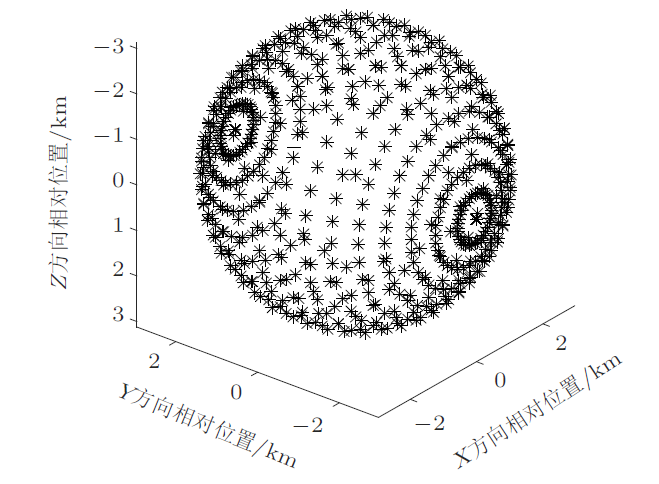
MATLAB为遍历计算仿真提供了便利,假设对一个航天器沿各个方向施加等量脉冲,在时间较短时,可达区的形状近似为球形,这一结论同样可以从CW方程中推导得到,式(21)给出了时间较短时三个方向的运动轨迹表达式,在各个方向都近似匀速直线运动。
(21) $\left.\begin{array}{l}x(t) \approx \dot{x}_{0} t \\y(t) \approx \dot{y}_{0} t \\z(t) \approx \dot{z}_{0} t\end{array}\right\}$
而时间变长后,可达区则演变为一个椭球形。通过演示法,可以更直观地看到可达区的形状,假设目标运行在400 km的圆轨道,图9 和图10 分别给出了每隔10$^\circ$ 全向施加10 m/s脉冲后目标卫星的到达区域,图9 是300 s时的可达区域,图10 是1500 s的可达区域。
图9
图10
除了MATLAB和STK以外,航天工程大学姚红等学者开始利用GeoGebra辅助航天动力学教学,GeoGebra是一款动态数学软件,将几何、代数、表格、图形、统计和微积分汇集在一个易于使用的软件包中,支持科学、技术、工程和数学(STEM) 教育以及教学和学习创新[9 ] 。
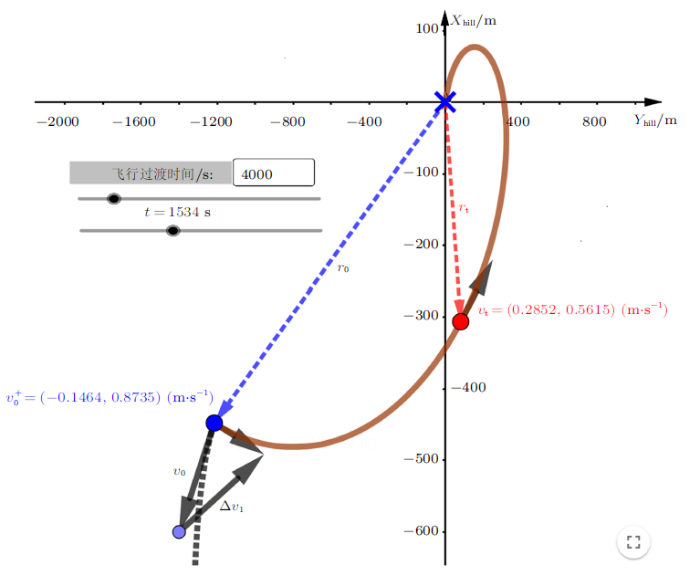
如图11 所示,GeoGebra与基于MATLAB和STK的教学方法相比,具有以下几个优点:(1)状态转移方程几何化显示,任何在绘图区所产生的教学对象,在代数区都会有一个代数表达式,通过LaTex格式导入状态转移方程,即可在绘图区展示交会接近轨迹;(2)具有动态滑杆功能,可自由拖动以改变交会时间,交会接近轨迹对应改变,更加直观动态展示两脉冲交会轨迹。
图11
图11
基于GeoGebra的不同时间交会轨迹示意图
4 结论
通过采用演示法、交互法和实验法相结合的体系化教学方法,达到化隐为显,化静为动,化虚为实的教学目的,将隐蔽的运动关系、相对运动方程经过化简、合并同类项转化为显式的关系,将静态的公式转化为动态的案例运用,将抽象的相对运动规律转换为直观的动画演示,有效地解决了本科生航天器相对运动教学过程中存在的公式推导多导致学习热情低、与经验知识相悖导致理解困难等问题。通过上机实践课,学员可自主开展交会与接近任务规划,进一步提升教学成效和学员实践能力,在结业考试中,相对运动试题的答对率在97%以上。
近3年来,空间维护原理课程教学团队利用军网"梦课"平台、各类培训班次、走进一线部队等方式宣传推广教学成果,取得了良好反响,课程教材入选军队"双重"重点建设教材,获批大学教学成果立项培育项目1项、"金课"培育项目1项。课程组始终瞄准人才培养目标,不断改革优化教学内容和教学方法,让学员深刻把握太空中运动的特点规律,在头脑中立起一幅生动的相对运动图景,学会基础理论的同时又掌握实践操作能力,为解决未来工作中的实际问题打下坚实基础。
参考文献
View Option
[1]
郗晓宁 , 王威 . 本科生课程教学中的互动—"航天器轨道力学基础"课程教学法简述
高等教育研究学报 , 2010 , 33 (1 ):82 -84
[本文引用: 1]
Xi Xiaoning Wang Wei . On interaction in teaching undergraduate course—teaching methods of fundamentals of spacecraft orbit dynamics
Journal of Higher Education Research 2010 , 33 (1 ):82 -84 (in Chinese)
[本文引用: 1]
[2]
罗亚中 , 李俊峰 , 高扬 等 . 基于"专家型"竞赛的航天创新人才培养模式与实践
力学与实践 , 2021 , 43 (2 ):262 -267
Luo Yazhong Li Junfeng Gao Yang , et al . Cultivation of innovative talents in aerospace based on "expert type" competition
Mechanics in Engineering 2021 , 43 (2 ):262 -267 (in Chinese)
[3]
杨洪伟 , 李爽 . 轨道力学问题导向式教学培养轨道设计能力的实践
力学与实践 , 2021 , 43 (2 ):268 -272
[本文引用: 1]
Yang Hongwei Li Shuang . The practice of training the ability of orbit design by problem-oriented teaching for orbital mechanics
Mechanics in Engineering 2021 , 43 (2 ):268 -272 (in Chinese)
[本文引用: 1]
[4]
党朝辉 . 航天器轨道动力学之"动"在何处?
力学与实践 , 2018 , 40 (2 ):236 -239
[本文引用: 1]
Dang Zhaohui . Why we talk of dynamics of a spacecraft orbit besides its kinematics?
Mechanics in Engineering 2018 , 40 (2 ):236 -239 (in Chinese)
[本文引用: 1]
[5]
王卫杰 , 张雅声 , 任元 等 . 基于STK 的航天器轨道动力学仿真教学方法研究
实验技术与管理 , 2020 , 37 (5 ):181 -185
[本文引用: 1]
Wang Weijie Zhang Yasheng Ren Yuan , etc. Research on simulation teaching method of spacecraft orbital dynamics based on STK
Experimental Technology and Management 2020 , 37 (5 ):181 -185 (in Chinese)
[本文引用: 1]
[6]
刁华飞 , 张雅声 , 程文华 . 掌握与精通STK . 北京 : 北京航空航天大学出版社 , 2021
[本文引用: 1]
[7]
Clohessy WH Wiltshire RS . Terminal guidance system for satellite rendezvous
Journal of Aerospace and Science 1960 , 27 (9 ):653 -658
DOI
URL
[本文引用: 1]
[8]
张雅声 . 弹道与轨道基础 . 北京 : 国防工业出版社 , 2019
[本文引用: 1]
[9]
王贵军 . GeoGebra与教学实验 . 北京 : 清华大学出版社 , 2018
[本文引用: 1]
本科生课程教学中的互动—"航天器轨道力学基础"课程教学法简述
1
2010
... 空间维护原理是我校运筹与任务规划专业本科学员的一门核心主干课程,讲述内容包括航天器轨道动力学和机械臂动力学,航天器轨道动力学又包括远程轨道机动动力学和近程轨道机动动力学,是航天领域的一门基础学科,对于培养航天专业人才具有重要意义[1 -3 ] .远程轨道机动需要用到绝对运动动力学模型,它是在惯性坐标系中建立的,用于描述航天器的绝对动力学特性;相对运动动力学模型是在目标轨道坐标系中建立的,用来描述追踪星相对目标星的动力学特性.航天器的相对运动类型包括交会对接、绕飞、跟飞、掠飞、悬停、编队飞行等.多个航天器相对运动轨迹具有瞬时变化和长期演化的特性,且在不同的参考坐标系中具有不同的形状,相对运动规律与地面的相对运动规律往往在直觉上是相悖的,对学员的空间想象力提出了较高的挑战.在授课过程中,学员难免会感到抽象乏味,难以将离散、抽象的数学公式与实际中的物理运动建立联系,普遍存在畏难情绪[4 ] . ...
本科生课程教学中的互动—"航天器轨道力学基础"课程教学法简述
1
2010
... 空间维护原理是我校运筹与任务规划专业本科学员的一门核心主干课程,讲述内容包括航天器轨道动力学和机械臂动力学,航天器轨道动力学又包括远程轨道机动动力学和近程轨道机动动力学,是航天领域的一门基础学科,对于培养航天专业人才具有重要意义[1 -3 ] .远程轨道机动需要用到绝对运动动力学模型,它是在惯性坐标系中建立的,用于描述航天器的绝对动力学特性;相对运动动力学模型是在目标轨道坐标系中建立的,用来描述追踪星相对目标星的动力学特性.航天器的相对运动类型包括交会对接、绕飞、跟飞、掠飞、悬停、编队飞行等.多个航天器相对运动轨迹具有瞬时变化和长期演化的特性,且在不同的参考坐标系中具有不同的形状,相对运动规律与地面的相对运动规律往往在直觉上是相悖的,对学员的空间想象力提出了较高的挑战.在授课过程中,学员难免会感到抽象乏味,难以将离散、抽象的数学公式与实际中的物理运动建立联系,普遍存在畏难情绪[4 ] . ...
基于"专家型"竞赛的航天创新人才培养模式与实践
0
2021
基于"专家型"竞赛的航天创新人才培养模式与实践
0
2021
轨道力学问题导向式教学培养轨道设计能力的实践
1
2021
... 空间维护原理是我校运筹与任务规划专业本科学员的一门核心主干课程,讲述内容包括航天器轨道动力学和机械臂动力学,航天器轨道动力学又包括远程轨道机动动力学和近程轨道机动动力学,是航天领域的一门基础学科,对于培养航天专业人才具有重要意义[1 -3 ] .远程轨道机动需要用到绝对运动动力学模型,它是在惯性坐标系中建立的,用于描述航天器的绝对动力学特性;相对运动动力学模型是在目标轨道坐标系中建立的,用来描述追踪星相对目标星的动力学特性.航天器的相对运动类型包括交会对接、绕飞、跟飞、掠飞、悬停、编队飞行等.多个航天器相对运动轨迹具有瞬时变化和长期演化的特性,且在不同的参考坐标系中具有不同的形状,相对运动规律与地面的相对运动规律往往在直觉上是相悖的,对学员的空间想象力提出了较高的挑战.在授课过程中,学员难免会感到抽象乏味,难以将离散、抽象的数学公式与实际中的物理运动建立联系,普遍存在畏难情绪[4 ] . ...
轨道力学问题导向式教学培养轨道设计能力的实践
1
2021
... 空间维护原理是我校运筹与任务规划专业本科学员的一门核心主干课程,讲述内容包括航天器轨道动力学和机械臂动力学,航天器轨道动力学又包括远程轨道机动动力学和近程轨道机动动力学,是航天领域的一门基础学科,对于培养航天专业人才具有重要意义[1 -3 ] .远程轨道机动需要用到绝对运动动力学模型,它是在惯性坐标系中建立的,用于描述航天器的绝对动力学特性;相对运动动力学模型是在目标轨道坐标系中建立的,用来描述追踪星相对目标星的动力学特性.航天器的相对运动类型包括交会对接、绕飞、跟飞、掠飞、悬停、编队飞行等.多个航天器相对运动轨迹具有瞬时变化和长期演化的特性,且在不同的参考坐标系中具有不同的形状,相对运动规律与地面的相对运动规律往往在直觉上是相悖的,对学员的空间想象力提出了较高的挑战.在授课过程中,学员难免会感到抽象乏味,难以将离散、抽象的数学公式与实际中的物理运动建立联系,普遍存在畏难情绪[4 ] . ...
航天器轨道动力学之"动"在何处?
1
2018
... 空间维护原理是我校运筹与任务规划专业本科学员的一门核心主干课程,讲述内容包括航天器轨道动力学和机械臂动力学,航天器轨道动力学又包括远程轨道机动动力学和近程轨道机动动力学,是航天领域的一门基础学科,对于培养航天专业人才具有重要意义[1 -3 ] .远程轨道机动需要用到绝对运动动力学模型,它是在惯性坐标系中建立的,用于描述航天器的绝对动力学特性;相对运动动力学模型是在目标轨道坐标系中建立的,用来描述追踪星相对目标星的动力学特性.航天器的相对运动类型包括交会对接、绕飞、跟飞、掠飞、悬停、编队飞行等.多个航天器相对运动轨迹具有瞬时变化和长期演化的特性,且在不同的参考坐标系中具有不同的形状,相对运动规律与地面的相对运动规律往往在直觉上是相悖的,对学员的空间想象力提出了较高的挑战.在授课过程中,学员难免会感到抽象乏味,难以将离散、抽象的数学公式与实际中的物理运动建立联系,普遍存在畏难情绪[4 ] . ...
航天器轨道动力学之"动"在何处?
1
2018
... 空间维护原理是我校运筹与任务规划专业本科学员的一门核心主干课程,讲述内容包括航天器轨道动力学和机械臂动力学,航天器轨道动力学又包括远程轨道机动动力学和近程轨道机动动力学,是航天领域的一门基础学科,对于培养航天专业人才具有重要意义[1 -3 ] .远程轨道机动需要用到绝对运动动力学模型,它是在惯性坐标系中建立的,用于描述航天器的绝对动力学特性;相对运动动力学模型是在目标轨道坐标系中建立的,用来描述追踪星相对目标星的动力学特性.航天器的相对运动类型包括交会对接、绕飞、跟飞、掠飞、悬停、编队飞行等.多个航天器相对运动轨迹具有瞬时变化和长期演化的特性,且在不同的参考坐标系中具有不同的形状,相对运动规律与地面的相对运动规律往往在直觉上是相悖的,对学员的空间想象力提出了较高的挑战.在授课过程中,学员难免会感到抽象乏味,难以将离散、抽象的数学公式与实际中的物理运动建立联系,普遍存在畏难情绪[4 ] . ...
基于STK 的航天器轨道动力学仿真教学方法研究
1
2020
... 课程组借用信息化手段,同步开设了空间维护原理线上课程,探索翻转课堂、线上线下相结合的混合式教学模式,满足学员的个性化学习需求.重视基于板书、MATLAB和GeoGebra的公式推导,充分体现逐步引导学生学习、引导学生思维的过程.将数学模型中的各物理量与物理模型建立联系,借助成熟STK软件中的三维和二维显示功能以及其他仿真软件[5 -6 ] ,构设虚拟仿真实验环境,展示太空中两个航天器的相对运动过程,通过将抽象的概念具体化帮助学生理解相关的理论. ...
基于STK 的航天器轨道动力学仿真教学方法研究
1
2020
... 课程组借用信息化手段,同步开设了空间维护原理线上课程,探索翻转课堂、线上线下相结合的混合式教学模式,满足学员的个性化学习需求.重视基于板书、MATLAB和GeoGebra的公式推导,充分体现逐步引导学生学习、引导学生思维的过程.将数学模型中的各物理量与物理模型建立联系,借助成熟STK软件中的三维和二维显示功能以及其他仿真软件[5 -6 ] ,构设虚拟仿真实验环境,展示太空中两个航天器的相对运动过程,通过将抽象的概念具体化帮助学生理解相关的理论. ...
1
2021
... 课程组借用信息化手段,同步开设了空间维护原理线上课程,探索翻转课堂、线上线下相结合的混合式教学模式,满足学员的个性化学习需求.重视基于板书、MATLAB和GeoGebra的公式推导,充分体现逐步引导学生学习、引导学生思维的过程.将数学模型中的各物理量与物理模型建立联系,借助成熟STK软件中的三维和二维显示功能以及其他仿真软件[5 -6 ] ,构设虚拟仿真实验环境,展示太空中两个航天器的相对运动过程,通过将抽象的概念具体化帮助学生理解相关的理论. ...
Terminal guidance system for satellite rendezvous
1
1960
... 绝对动力学模型一般采用数值解法,可用来精确分析航天器的动力学特性.相对运动动力学模型中应用最广泛的是Clohessy-Wiltshire (CW)方程[7 ] ,它具有简单的线性常系数形式,可用来直观分析相对运动的动力学特性,需要结合推导过程提醒学员的是,CW方程成立的假设是目标运行在原轨道,相对距离较近且忽略了高阶摄动力. ...
1
2019
... 式(3)给出了描述绝对运动的高斯摄动方程[8 ] ,从第一个和第二个等式中可以看出,当目标轨道偏心率为零时,施加径向方向的小脉冲只会改变轨道的偏心率,不改变轨道半长轴大小. ...
1
2018
... 除了MATLAB和STK以外,航天工程大学姚红等学者开始利用GeoGebra辅助航天动力学教学,GeoGebra是一款动态数学软件,将几何、代数、表格、图形、统计和微积分汇集在一个易于使用的软件包中,支持科学、技术、工程和数学(STEM) 教育以及教学和学习创新[9 ] . ...