基础力学是土建类专业的重要技术基础课,对专业课的学习起到承上启下的作用,吸收弹性力学作为"后备力量",可发挥力学分析的优势^[1-2]。当前,在"双创"教育背景下,部分高校工科专业学时不断压缩,尤其是基础力学。减小理论教学与实践应用脱节带来的不利影响,可通过开放实验弥补这一空隙^[3-5]。一些成功的教学探索表明,开放实验教学可以充分吸收实践研究理念,通过设置与理论教学内容相关的课目能够强化学生的力学基础知识和实践能力,从而提升学生的综合素质^[6-8]。

针对基础力学的教学现状,近年在防灾科技学院开展了以开放实验为重要载体的教学模式改革与探索实践,本文列举了材料力学中内压薄壁圆筒的应力分析问题,以此介绍开放实验的全过程及其效果达成度,为进一步将开放实验打造为联系基础力学与实践应用的纽带提供案例参考。

受内压的薄壁圆筒应力分析是材料力学中的一道典型例题,与工程中的油气罐、煤气罐、易拉罐等薄壁容器具有相似性。材料力学中仅讲解了筒壁的正应力计算,对公式的完整性以及内压对筒壁的影响并未深入介绍。通过开放实验可将这一典型例题所隐含的知识点充分挖掘,发挥理论知识的应用性和教学的高阶性,从而把枯燥乏味的力学公式转变为生动有趣的研究探索,提高基础力学学习效果。

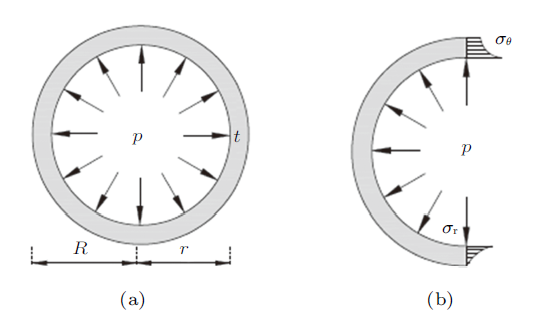
工业中的油气罐、轿车后箱中的气罐以及常见的易拉罐等都可视为薄壁圆筒结构,如图1所示。内压作用下筒壁的应力如何求解,可通过力学简化和建立平衡方程加以阐述,此部分内容可映射材料力学轴向拉压和应力状态章节的重要知识点。

作为开放实验,选取生活中常见的易拉罐为研究对象,根据截面法可得罐体的受力简图如图2所示^[1]。

定义易拉罐的壁厚为$t$,内径为$r$,外径为$R$,内压为$p$,$m$-$n$截面间的罐体长度为$b$。水平放置的易拉罐结构及载荷均具有对称性,没有切应力,所以罐体表面微元上的环向应力$\sigma_{1}$和轴向应力$\sigma_{2}$就是两个主应力,$P_{1}$和$P_{2}$分别代表内压在罐体柱面投影面和罐体底面上的合力,如图2所示。对于环向应力,截取$m$-$n$截面中的罐体为研究对象,如图2(b)所示。将内压$p$映射在柱面投影面上,根据环向力的平衡方程可知

则有$\sigma_{1} =pr/t$。

由于壁厚$t$要远小于罐体的半径,所以轴向应力可视为均匀分布在壁厚上,如图2(c)所示。将内压$p$投影在罐体底面上,由轴向应力的平衡方程可知

则有$\sigma_{2} =pr/2t$。

对比可以发现,环向应力是轴向应力的2倍。弹性力学通过逆解法也给出了薄壁圆筒的应力解析解,且应力分布是轴对称的,如图3所示^[2]。

对只存在内压$p$的薄壁圆筒,其径向应力$\sigma_{\rm r}$和环向应力$\sigma_{\theta }$可以表示为

式中$\rho $为径向参数,当$\rho =R$,可知$\sigma_{\rm r}=0$。而$\sigma_{\theta }$可以进一步整理为

由于罐体壁厚$t$远小于半径$r$,则$\left( {{t}/{r}} \right)^{2}\approx0$,可得到

由此可知,弹性力学环向应力$\sigma_{\theta}$和材料力学得到的环向应力$\sigma_{1}$是相同的。式(1)~式(5)完全展现了两门力学课程基础知识的贯通性,这对掌握和理解应力状态和解析理论有巨大帮助。

在理论分析的基础上,如何设置开放实验是关键。生活中,当用手振动碳酸饮料时,会发现易拉罐表面绷紧,有张力感,那么振动后易拉罐内部的压力究竟有多大呢?易拉罐会不会爆炸?如何测量内压呢?基于上述问题的思考,与学生共同讨论设定了易拉罐应力测试趣味开放实验,目的是测试罐体内部的压力大小以及校验罐体材料的强度。实验分为两部分进行,第一部分测试易拉罐体的强度参数,第二部分对罐体的应力进行测试。

实验采用两片式3104铝合金制造的通用易拉罐,其力学参数为：弹性模量为70 GPa,泊松比为0.3^[9-11]。为确定出罐体材料的屈服极限和强度极限,需自己制作试件。试件由小组同学将罐体截开,通过查阅《金属材料拉伸试验第1部分：室温试验方法》的规范要求,制作了3个标准试件,如图4所示。经游标卡尺测定出试件的平均直径$r=62.32$ mm,厚度$t=0.11$ mm。

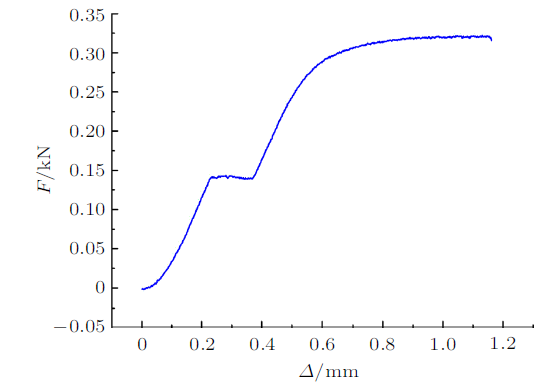
通过MTS试验机完成试件的载荷-变形曲线测试。受试件几何尺寸影响,测试前需调整试验机加载模具和参数,本次实验通过调整位移速率来控制,速率控制为0.001 mm/s。将试件缓慢加载至破坏,提取3个试件拉伸实验数据平均值,绘制载荷-变形曲线,如图5所示。从图5可以看出,3104铝合金屈服平台明显是一典型的塑性材料。根据轴向拉压应力公式计算得到材料的屈服极限为131.82 MPa,强度极限为295.45 MPa。

易拉罐压力测试方法选用电测法,通过获取不同测点在开启前和开启后的应变变化值来反演罐体内部压力,实验过程要求小组学生独立完成并相互检查过程质量。

3.2.1 实验过程

(1) 在易拉罐周身选取应变片粘贴点,用划针进行标记。测点位置包括罐顶平行于拉环方向测点1#、罐底中心正交方向测点2#和3#、罐体侧壁45$^\circ$应变花方向测点4#~6#,并用AB胶紧密与罐体粘贴,压实防止产生气泡。

(2) 裁剪适合的引线长度,将导线与引线焊接在端子上,本次实验应变片为BE120-3AA型。

(3) 检查应变片粘贴质量,外观重点检查是否有脱胶和翘曲现象,再通过万用表测试应变片是否存在短路或阻值不稳定现象,粘贴完整应变片的易拉罐如图6(a)所示。

(4) 将导线与XL2118静态电阻应变仪连接,应变仪采用1/4桥路并连接温度补偿片,设置6个通道以记录应变片的数据。

(5)振动易拉罐20 s后将罐体水平放置,观察应变仪上的数据,待数值稳定后,记录数据;开启拉环,继续观察应变值的变化,待稳定后,再次记录数据,开启后应变仪数据如图6(b)所示。

(6)将开启后和开启前的应变差代入广义胡克定律式(6)求解薄壁表面的应力。通过环向应力式(1)和轴向应力式(2)反解出罐体内压$p$。

3.2.2 内压分析

将开启后的易拉罐视为基态,计算开启前与开启后不同罐体测点的应变差值,结果如表1所示。

从表1可以看出,反解出的内压基本相同,三次实验所得的内压均值分别为0.28 MPa和0.26 MPa,偏差仅为7.15%。理论上,基于式(1)和式(2)反解的内压应是相同的,但实验过程中不可避免地存在一定的误差,因此二者在实验数据上有所差别。通过分析可知,内压均值偏差小于10%,说明实验是成功的,即可推断罐体实际内压介于2.5~3个大气压之间。

3.2.3 强度校验

罐体强度校验通过罐顶和罐底正交方向的3个应变片来完成,三次实验所获得的测点开启前与开启后的应变差值如表2所示。

根据胡克定律计算出测点应力：罐顶最大应力为80.29 MPa,由第一强度理论可知计算值小于实测罐体的屈服强度131.82 MPa;由第四强度理论可知,罐体侧壁最大相当应力为71.72 MPa,也小于罐体的屈服强度;综合各测点应力值可以推断罐体自身强度是安全的。

3.2.4 实验结果讨论

市场上碳酸饮料是含有二氧化碳的汽水,摇晃之后二氧化碳会释放,气压会持续地增大。内压作用下,打开罐体会喷出一定的饮料,但内压过大并非有利。过大的内压造成罐体所受应力过大,不利于安全。为了保证罐体在储运过程中

的安全,罐体底部一般设计为凹形,就是为了抵御内压过大产生的膨胀变形。针对上述问题,通过理论分析和实验测试方法可估算出罐体内压,这对运用材料力学基础知识向实践应用转化具有重要意义,应该作为本科生在开放实验训练中的重点。

3.2.5 工程扩展

石油储气罐、液化气罐、储油罐等工业容器也是典型的薄壁圆筒结构,与易拉罐的应力分析具有高度同源性。在内压的作用下,筒壁结构是否安全,均可用上述理论分析和讨论。因此,薄壁圆筒的应力分析可以从理论、实验向工程应用扩展,以此提高力学基础理论的应用性。

薄壁圆筒应力分析开放实验以我院土木工程专业为试点,本项实验先后有两批次,共27人参与。实验过程中,采用教师指导、学生主动的模式,相继完成试件制作、强度参数测试、应变片粘贴、质量检测以及内压测试和数据处理等环节,并基于理论分析和实验数据得到了易拉罐的内压。在分组讨论环节中,根据内压的大小,与学生共同讨论了易拉罐的外形设计,并扩展至工程中的薄壁罐体。通过学生主导实验过程,有效地提高了学生的文献查阅能力和实验动手能力,同时也培养了学生严谨的工作作风。

实验完成后通过问卷调查和座谈的方式对学生的学习状态和学习效果进行分析和总结,除常规问卷调查外,总结学习兴趣、实验操作、学习效果、工程拓展和综合运用5项指标点的达成度,统计各指标百分比如图7所示。

从图7可以看出,学生对本项实验持有积极态度,认为开放实验串联了力学中的基础知识点,对实验中所反映出的工程问题有所体会,对专业综合能力的提升有一定的促进作用。本项实验达成度百分比最高的是学习兴趣,由此可知兴趣牵引是学习的主要动力。而达成度最低的是综合运用,仅为71%,较其他指标低,也是整个实验过程中暴露出的最大显现问题,可见在问题的理论剖析和实验测试方面还有待加强,对问题的科学分析亦应强化。因此,提高学生的综合应用能力应作为后续开放实验改革的重点。

基于此,总结本次开放实验的教学效果包括以下几点。

(1) 薄壁圆筒应力计算是轴向拉压杆件的典型例题,通过开放实验可以系统地串联材料力学和弹性力学中的相关知识点,包括：截面法、轴向拉压应力计算公式、应力分布理论公式、广义胡克定律、强度理论、拉压实验以及电测法实验等;

(2) 薄壁圆筒的应力分析与工程中的储气罐等容器受内压问题大同小异,设置的小组讨论环节对深入认知薄壁圆筒所隐含的工程问题有一定的积极作用,有利于培养学生的工程意识,在实验教学中具有一定的示范意义;

(3) 本次开放实验源于生活趣事,又引申出工程问题,在题目设置和实现上应用了理论分析、实验测试和工程扩展三个重要手段,体现了开放实验的趣味性和专业性,弥补了常规实验的不足。

基础力学是土木工程专业知识体系的重要基石,利用开放实验扩展力学知识,科学设计趣味实验和专业实验可将理论分析、实验操作和工程应用有机地结合起来,具有一定的可行性。后续开放实验课目设置将在本次实验的基础上进行改革和创新,并融合虚拟仿真实验,以期将开放实验打造成理论与实践联系的重要纽带,成为实验教学的重要载体。