在结构力学中,一般通过三个静定结构几何组成规则(三刚片规则、二刚片规则、二元体规则)来判断简单平面体系的几何组成,而复杂平面体系的几何组成分析需要应用零载法来完成^[1]。由于复杂平面体系内力与反力计算过程繁琐,而零载法需要计算体系的全部内力与反力才能对体系的几何组成性质做出判断,因此,现有零载法分析复杂平面体系的几何组成可能需要一个复杂的计算过程。

在复杂静定平面桁架的计算中,用结点法、截面法求解可能要求解较多联立方程,杆件替代法被认为是一种有效的解题方法。由于复杂平面体系的几何组成分析不是结构力学的教学重点,结构力学教师对如何快速地用零载法来计算与判断复杂平面体系的几何组成分析并没有多少兴趣,杆件替代法并没有与零载法一起用于计算并判断复杂平面体系几何组成。

为了简化复杂平面体系的几何组成分析,充分利用杆件替代法计算复杂静定平面体系的优势,本文将杆件替代法与零载法结合起来,利用静定结构的受力特性,建立了复杂平面体系几何组成分析的基本规则。最后,通过算例分析论证了本文建立的复杂平面体系几何组成分析基本规则的可行性与优越性。

零载法只能用于计算自由度等于零的平面体系的几何组成分析,其理论依据是静定结构解答的唯一性定理,即无载荷作用时静定结构不可能有非零反力和内力。如果体系存在非零反力和内力,则该体系是几何可变体系。

零载法的具体分析步骤为^[2]：

(1) 求体系的计算自由度$W$,$W$应等于零。

(2) 去掉肯定为零的轴力杆简化体系。

(3) 设某内力或反力为非零值$X$,分析在满足全部平衡条件时$X$的值。

(4) 如果$X$等于零,则体系为静定结构;如果存在非零值$X$,则体系为几何可变。

图1所示体系^[3]计算自由度$W =0$,应用零载法分析该体系。首先假设水平支座链杆$F$的反力为$X$,由结点法可求出各杆轴力及各支座反力,结果如图2所示。可见载荷为零但体系内力与反力存在非零值$X$ (自内力),故图1体系为几何可变体系。

一般认为,杆件替代法是计算复杂静定平面桁架结构的有效方法,但这种方法显然能用于其他型式的复杂静定平面结构的计算。杆件替代法的基本思路是^[3-4]：通过轴力杆件(包括支座链杆)之间的替代,简化复杂静定平面结构的几何组成,然后再将简化后的静定平面结构杆件的内力恢复到原结构的状态。

图3(a)所示复杂静定平面桁架可以按结点法与截面法联合应用进行求解,但这种方法需多次建立联立方程。下面介绍如何运用杆件替代法来求解。

若将该桁架$C$支座处的链杆拆除,而代之以$E$和$F$之间增设轴力杆,则可得到图3(b)所示的简单桁架(替代结构),此时替代结构内力易求得,其中$F_{NEF} =3.6F_{P}$。为使杆件替代后,所得桁架(替代结构)的内力与原结构相同,可在替代结构$C$支座处作用未知反力$X$ (如图3(c)),此时可求得$F_{NEF}=3X$。因为实际结构中并不存在$EF$杆,所以$C$支座真实的反力应使图3(b)、图3(c)所示替代结构受力状态叠加后,$EF$杆的内力为零,即

解得

通过以上杆件替代求得$C$支座反力$X$之后,由图3(b)、图3(c)所示替代结构受力状态叠加即得原桁架的内力与反力,如图3(d)所示。

显然,如果图3(e)所示简单桁架中$EF$杆的内力为零,则3(a)所示复杂静定平面桁架与图3(e)所示简单桁架的受力状态是等效的。此外,替代杆件的位置不是唯一的,如$BD$杆也可以作为替代杆件,选择替代杆件位置的条件是必须保证替代结构较原结构计算更加简便。

本文采用零载法分析平面体系的几何组成,但平面体系各杆件内力计算采用杆件替代法。

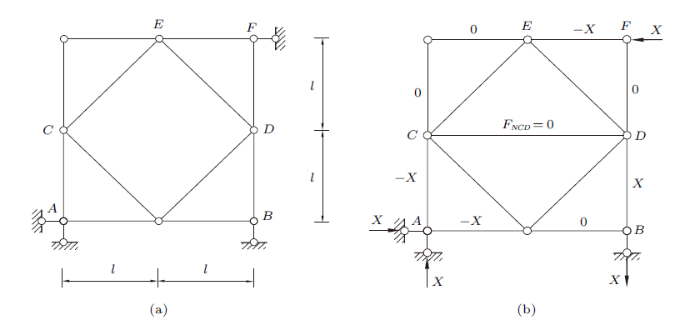
图4(a)所示为复杂平面铰接体系,用结构力学中的简单几何组成规则难以判断其几何组成,下面介绍用零载法与杆件替代法计算并分析其几何组成。

将该体系$C$支座处的链杆拆除,用反力$X$代替其作用,为保持桁架的几何不变性质,在$E$、$F$之间增设轴力杆,可得到图4(b)所示的简单桁架。图4(b)所示简单桁架在反力$X$作用下的杆件$EF$内力由截面法极易求得为$F_{NEF}=3X$。显然,图4(a)所示体系与图 {4(b)} 所示简单桁架等价的条件是图 {4(b)} 所示简单桁架中$EF$杆的内力为零,即$F_{NEF}=$0$,故可解得反力$X$为零。由于图4(b)所示为简单桁架,即内力与反力必为零,而图4(a)所示体系与图4(b)所示简单桁架等价,也即图4(a)所示体系在零载荷作用下所有内力与反力也为零,故图4(a)所示体系为静定结构。本文分析方法的关键在于计算替代杆件轴力$F_{NEF}$,只要替代杆件轴力与$X$相关,即可判定原体系为静定结构。

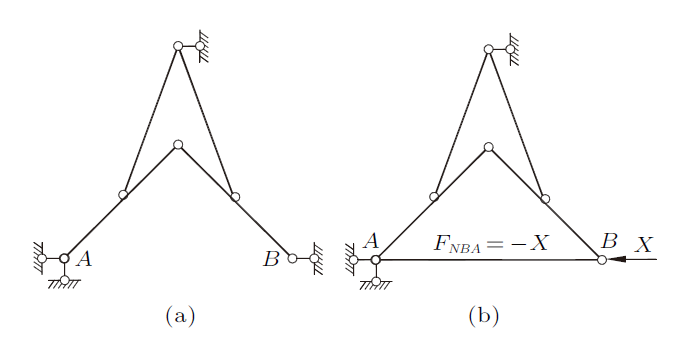
图5(a)所示为复杂平面铰接体系,前面已用零载法判断其为可变体系,下面介绍用零载法与杆件替代法计算并分析其几何组成。

将该体系$F$支座处的链杆拆除,用反力$X$代替其作用,为保持桁架的几何不变性质,在$C$、$D$之间增设轴力杆,可得到图5(b)所示的简单桁架。图5(b)所示简单桁架在反力$X$作用下的杆件$CD$内力由截面法极易求得为$F_{NCD}=0$,也即替换杆件轴力与反力$X$无关。同时注意到图5(a)所示体系与图5(b)所示简单桁架的受力状态是等效的,可见载荷为零但体系内力与反力存在非零值$X$,故5(a)所示体系为几何可变体系。本文分析方法的关键在于计算替代杆件轴力$F_{NCD}$与反力$X$无关,即替代杆件轴力恒等于零,故可判定原体系为几何可变体系。

综合上述示例分析,本文得到了应用杆件替代法与零载法相结合判断平面体系几何组成的基本规则为：去除某支座链杆或体系中链杆,用力$X$代替其作用。同时将去除的支座链杆或体系中链杆替换到体系中相应位置,使体系成为静定结构。如果替换支座链杆反力或体系中替换链杆轴力与力$X$有确定关系,则原体系为静定结构,否则为几何可变体系。

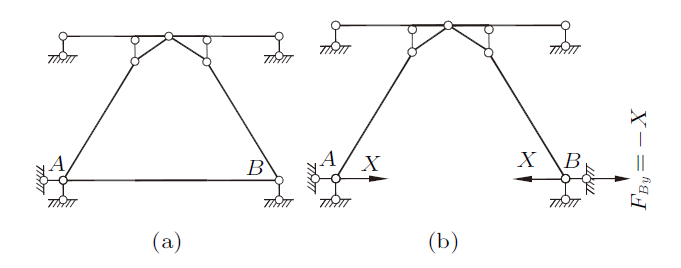
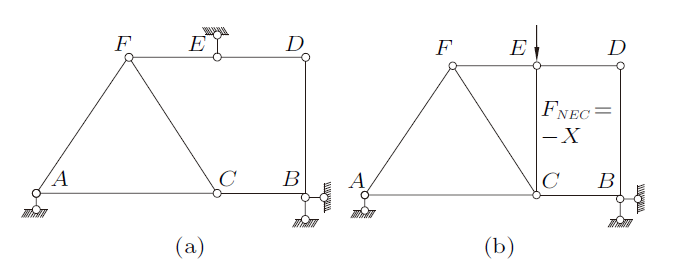
图6(a),图7(a),图8(a)所示为复杂平面体系,其几何组成无法由结构力学三个静定结构几何组成规则来判断,下面用本文方法来分析其几何组成。对于图6(a)所示体系,可去除$B$支座链杆,用力$X$代替其作用,同时将$B$支座链杆替换到体系中$A$和$B$位置,如图6(b)所示,替换后体系显然是一简单静定结构,由静定平衡条件可极易得到替换链杆$AB$的轴力为$F_{NAB}=-X$,由本文基本规则可确定该体系为静定结构。同理可判断图7(a)所示体系为静定结构。以上两例是把支座链杆替换成轴力杆件,在分析图8(a)体系几何组成时,则是把杆件$AB$替换为$B$支座链杆,同样可应用本文基本规则确定该体系为静定结构。本文方法不仅可用来判断复杂平面体系的几何组成,对于应用结构力学静定结构几何组成规则判断十分困难的如图9(a)所示的一般平面体系,也能非常简捷地确定其为静定结构。

图10(a)所示体系是结构力学的一个经典分析示例^[1-3],应用结构力学静定结构几何组成规则判断十分困难。如果应用本文方法,可去除$C$支座链杆,用力$X$代替其作用,同时将$C$支座链杆替换到体系中$E$和$F$位置如图10(b)所示,替换后体系显然是一简单静定桁架结构,由对称性与零杆判断方法可极易得到替换链杆$EF$的轴力为$F_{NEF}=0$,由本文基本规则可确定该体系为可变体系。

(1) 本文应用杆件替代法与零载法相结合提出的判断平面体系几何组成的基本规则,适用于计算自由度$W =$0的包括复杂平面体系在内的任何平面体系,弥补了现行结构力学静定结构几何组成规则难以判断复杂平面体系几何组成的不足。

(2) 与零载法判断平面体系需要计算体系全部内力与反力不同,本文提出的判断平面体系几何组成的基本规则只需要计算替换支座链杆反力或体系中替换链杆轴力。由于可以根据简便计算需要选择替换杆件的位置,从而大幅度地提高了平面体系几何组成分析的效率,减少了因计算量大而可能出现的错误判断。

(3) 算例分析表明,本文提出的判断平面体系几何组成的基本规则是高效可行的,可编入结构力学教材供学生学习应用。