材料力学课程中,在推导出直杆的偏心拉(压)正应力计算公式后,得到了中性轴方程,然后自然地引出了截面核心^[1-5]的概念。要引导学生深入理解截面核心的概念,可尽可能多地给出不同截面形状的截面核心的例子。为此,我们借鉴了相关先进经验^[6-8],编写了相应的MATLAB程序,实现了可视化教学。计算过程中,需要计算截面的面积、静矩、惯性矩和惯性积等平面图形的几何性质。教材^[1]中给出了计算这些几何量的近似方法。我们利用散度定理给出了一种新的数值计算方法。

如果对截面核心的教学到此为止,深度似乎有所不足。范钦珊等^[9]提出"课程教学改革的思路是：注重基础,挖掘深度,适当扩展,面向未来"。薛秀丽等^[10]提出"适当扩展课程内容,激发学生的学习兴趣"。所以,我们在列举出若干截面核心的实例后,引导学生探究截面核心的一个性质—外凸性。事实上,该性质容易被忽视,如教材^[5]截面核心示意图中截面核心不是外凸的。王道敏^[11]讨论了截面核心的性质,用几何方法证明了当横截面为多边形时截面核心是包围形心的凸多边形。我们运用静力等效和叠加原理从力学角度解释了该性质,也从数学上证明了截面核心是凸集。

我们希望通过这样的教学安排,学生能够对截面核心概念有清晰的认识,在课堂上"有实实在在的获得感,或者有学而收获的预期"^[12],同时,我们希望强化一种思考方法：对新事物,首先经过大量的观察,建立初步的认识,再思考猜测其性质,最后证明猜想,完成从感性认识到理性认识的升华。

考虑受偏心拉伸的直杆。在杆的端部建立如图1所示的坐标系,坐标系的原点位于截面的形心。在杆的端部受集中力$F$的作用,力$F$的作用点坐标为$M\left({y_{F},z_{F} } \right)$,方向与杆的轴线平行。

在点$M\left( {y_{F},z_{F} } \right)$处作用与轴线平行的力$F$时,直杆的受力形式为偏心拉伸(压缩),依组合变形的叠加原理,其横截面上任意一点$C\left({y,z} \right)$处的正应力为^[1-5]

这里$A$为直杆的横截面面积,$i_{y} $和$i_{z}$为惯性半径,均为常数。在式(1)中令$\sigma =0$可得到中性轴的方程为

土建工程中常用的混凝土构件和砖、石砌体,其拉伸强度远低于压缩强度,这就要求杆件在受偏心压力作用时,其横截面上不出现拉应力,即应使中性轴不与横截面相交。当外力作用点位于截面形心附近的一个区域内时,可保证中性轴不与横截面相交,这个区域称为截面核心。

截面核心的计算过程教材已经给出,在此不再赘述。计算过程中需要求解平面图形的几何性质,这里给出一种边界积分的方法。本方法有别于教材^[1]中的近似方法,计算精度高,编程实现简单。

在微积分课程中已经得到散度定理,即

式中,$\varOmega $和$\partial \varOmega $分别表示积分域及其边界,${n}$表示边界的外法线方向,${B}$表示某向量场。现在考虑某标量$T$的面积分$\displaystyle\int_\varOmega {T{\rm d}\varOmega } $。为了将面积分转化为边界积分,可构造向量${B}$,使得

则有

当标量$T$的形式比较简单(如多项式)时,向量${B}$易于构造,对标量$T$的面积积分就容易转换为向量${B}$的边界积分。对于式(5)中的边界积分,可先对边界进行单元剖分,然后逐单元积分,最后求和。当边界的某部分为直边时,该部分只划分为一个单元;当边界是曲边边界时,为保证精度需要划分为多个单元。

对面积、静矩、惯性矩和惯性积的计算,只需恰当选择式(5)中的向量函数${B}$即可。这里给出求各几何量对应的向量函数${B}$以及最终采用线性单元时的线积分计算公式,如表1所示。

式(6)~式(11)中,$y$和$z$是节点的坐标,下标1和2表示单元的节点编号,$n$是单元数。公式应用条件为边界节点按逆时针方向排列。

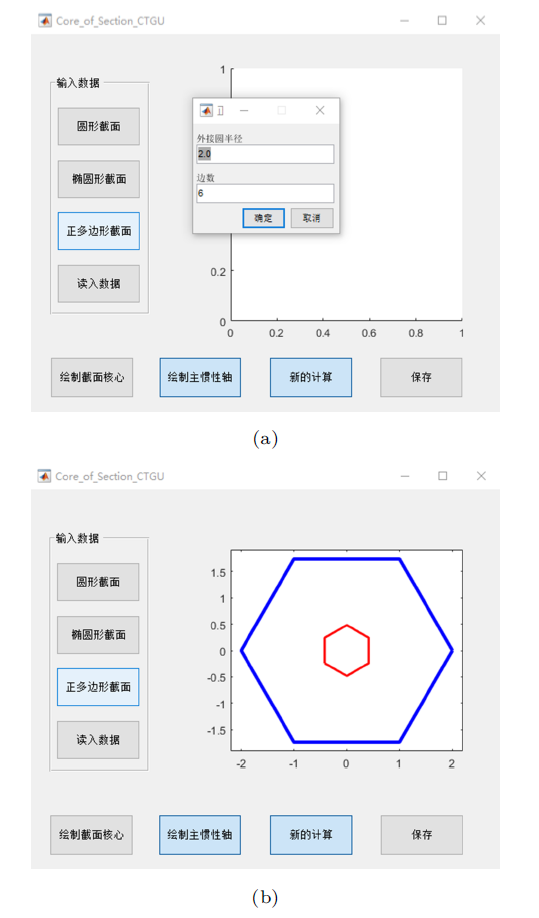
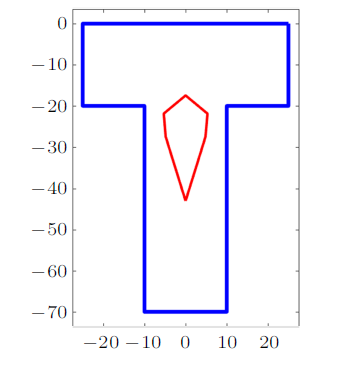
教学过程中,运用自编的MATLAB程序计算了若干不同形状截面的截面核心。程序对形状规则的截面,如圆、椭圆、正多边形等,可直接输入相关参数进行计算,对于复杂的图形,可读入图形的边界点的坐标进行计算,如图2所示。因版面所限,这里仅仅给出几例,如图3~图6所示。特别地,为了增加趣味性,给出了心脏线形截面的截面核心,这也是下一个话题的引子。

教学中,在给出了图5所示心脏线形截面的截面核心后,抛出一个问题：是否存在一个截面,其截面核心是心脏线形状?

经过前面展示多个不同形状截面的截面核心,可引导学生思考、猜测截面核心的共同特征：外凸的。如果这个猜测是正确的,那么上述问题的答案就是否定的,只可能是图6所示的近似心脏线形状。下面的工作就是证明该猜想。首先基于静力等效和叠加原理从力学上解释截面核心不可能是凹的,再在给出凸集定义的基础上,从数学上严格证明这一猜想。

假设截面核心是凹的,如图7所示。设点$A$和点$B$在截面核心内,点$C$在$A$和$B$连线上且位于截面核心外。记$AC$的长度为$l_{AC}$,$BC$的长度为$l_{BC} $。现在$C$点作用压力$F_{C}$,因为点$C$不属于截面核心,所以横截面上既有拉应力,也有压应力。

考虑另外一种情况：在点$A$和点$B$同时作用压力$F_{A} $和$F_{B} $,且有

则根据叠加原理,横截面上只有压应力,没有拉应力。

然而,上述两种情况是静力等效的,不应该在横截面上出现不同的应力分布。矛盾源于截面核心是凹的假设。这就从力学上解释了截面核心不可能是凹的。

为了使得证明过程清晰,首先给出平面上凸集的定义,再提出两个命题,最后用这两个命题证明最终结论。

3.2.1 凸集的定义

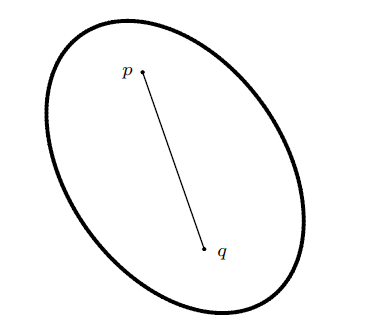
按文献^[13,14]给出平面上凸集的定义：对集合$K\subset {R}^{2}$,如果任意给定两点$p,q\in K$,直线段$\overline {pq} $包含在$K$中,则称$K$是凸集,如图8所示。

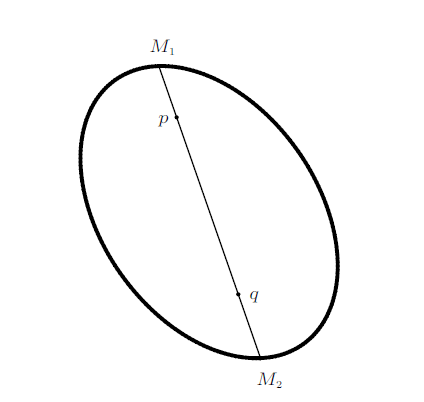
在集合$K\subset {R}^{2}$的边界上任取两点$M_{1} $和$M_{2}$,如果证明了线段$\overline {M_{1} M_{2} }$上的任何一点都属于$K$,那么$K$是凸集。因为对于任意给定两点$p,q\in K$,总可以作通过点$p$和$q$的直线与边界相交,交点记作$M_{1} $和$M_{2}$,如图9所示。如果线段$\overline {M_{1} M_{2} } $上的任何一点都属于$K$,那么线段$\overline {pq} $当然也包含在$K$中,根据凸集的定义,$K$是凸集。下文证明截面核心是凸集时正是采用了这种方法。

3.2.2 命题1

如图10所示,位于坐标原点$O\left( {0,0} \right)$两侧、相互平行的两直线$l_{1} $和$l_{2} $,其方程分别为

这里$k<0$,$a$和$b$不同时为0。另有直线$l$,其含参数$\lambda $的方程为

则当$0<\lambda <1$时,直线$l$在直线$l_{1} $和$l_{2} $外侧。

该命题的证明很简单,此处略。

3.2.3 命题2

不通过坐标原点$O\left( {0,0} \right)$的直线$l_{1} $和$l_{2}$,其方程分别为

它们相交于点$Q$。直线$l_{1} $和$l_{2}$将平面$Oyz$划分为四个角域,如图11所示。另有直线$l$,其含参数$\lambda$的方程为

则当$0<\lambda<1$时,直线$l$不会落在包含坐标原点$O$的角域内。

证明：由方程(15)和方程(16)以及直线族的定义知道,直线$l$通过直线$l_{1} $和$l_{2}$的交点$Q$。作通过坐标原点$O$且以直线$l_{1} $和$l_{2}$为渐近线的双曲线$s$,如图12所示。双曲线$s$的方程为

通过考察直线$l$与双曲线$s$是否相交来判断直线$l$是否落在包含坐标原点$O$的角域内。为此,当$0<\lambda <1$时,将直线$l$的方程(16)改写为

式(18)代入式(17)得到

显然,式(19)左端非正,故方程无解,直线$l$与双曲线$s$没有交点,即直线$l$不会落在包含坐标原点$O$的角域内。

3.2.4 截面核心是凸集的证明

在截面核心的边界上任取两点$M_{1}( y_{1},z_{1})$, $M_{2} \left( y_{2},z_{2} \right)$。与$M_{1}$点相对应的中性轴记作$l_{1} $,与$M_{2} $点相对应的中性轴记作$l_{2}$,按式(2)得到它们的方程为

连接$M_{1} M_{2} $,在线段$M_{1} M_{2} $上任取一点$M$,其坐标可表示为

这里,$0<\lambda <1$。与点$M$对应的中性轴记作$l$,按式(2)得其方程为

情况一：如果中性轴$l_{1} $与$l_{2} $平行,则由方程(20)和方程(22)知道,中性轴$l_{1}$,$l_{2} $和$l$相互平行,如图13所示。考虑到$l_{1} $和$l_{2}$与横截面相切,所以它们位于坐标原点$O$的两侧。由命题1知道,中性轴$l$必在中性轴$l_{1}$和$l_{2} $的外侧,即中性轴$l$与横截面不会相交,从而点$M$属于截面核心。

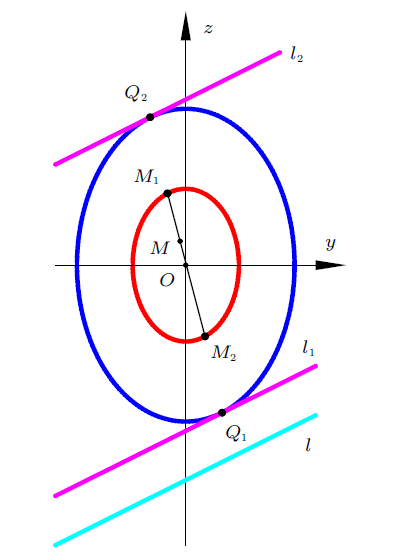
情况二：如果中性轴$l_{1} $与$l_{2}$不平行,则由方程(20)和方程(22)以及直线族的定义知道,中性轴$l$,$l_{1} $和$l_{2}$相交于同一点,记作$Q$,如图14所示。由命题2知道,中性轴$l$必不落在包含坐标原点$O$的角域内,即中性轴$l$与横截面不相交,从而点$M$属于截面核心。

综合上述两种情况,再由点$M_{1} $,$M_{2}$和$M$的任意性以及凸集的定义知道,截面核心是凸集。

为了讲好截面核心的概念,课前编写了截面核心的计算程序。给出了平面图形几何性质的边界积分数值计算方法。用该程序计算了多个不同形状截面的截面核心,使得学生对截面核心的概念有初步的了解。在列举出若干截面核心的实例后,引导学生探究截面核心的凸性。运用静力等效和叠加原理从力学角度解释了该性质,也从数学上证明了截面核心是凸集。这使得学生对截面核心有了进一步的理解。实践表明,这样的教学设计可以活跃课堂气氛,激发学生的学习兴趣,培养学生认识新事物的思考方法。