伽辽金法类属于加权残值法,在《有限元方法》和《计算结构力学》教科书中都会讲授[1 -2 ] 。该方法在具体应用时会涉及试函数的选取,通常要求试函数为一组线性无关的函数,并满足结构的所有位移和力边界条件。一些文献指出在难于选取满足所有边界条件的试函数时,可以选取仅满足位移边界条件不必满足力边界条件的试函数,通过增加试函数的个数弥补不满足力边界条件引起的误差。然而,这种简化与加权残值法的基本原理相违背,获得结果可能无法收敛于正确解。下面以计算同时受轴向力和横向分布力悬臂梁的横向位移和固有频率为例进行说明。
1 轴向力下悬臂梁横向位移和固有频率
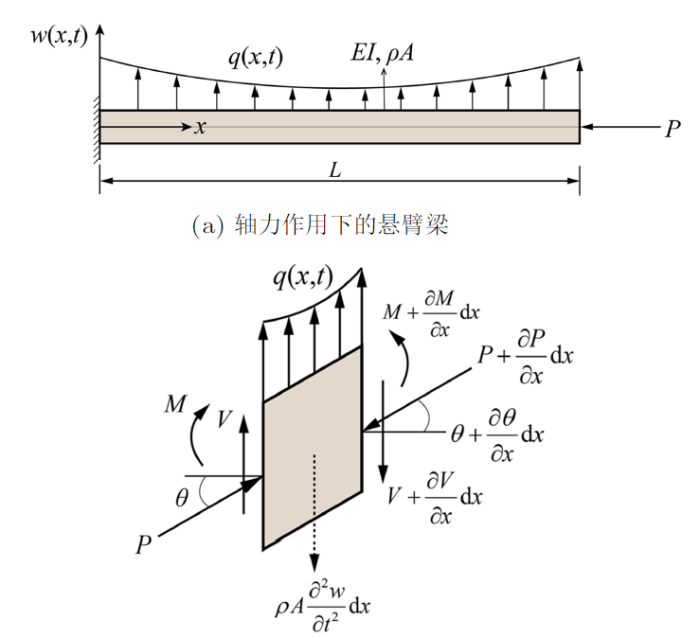
图1 (a)所示为端部受轴向力$P$作用的均匀悬臂梁,长度$L$,抗弯刚度$EI$,单位长质量密度$\rho A$,横向分布载荷$q(x,t)$,横向位移$w(x,t)$;其微段d$x$受力如图1 (b)示,图中$M$为弯矩,$V$为剪力,$\theta$为截面转角。梁微幅振动方程为
(1) $EI\frac{\partial^{4}w}{\partial x^{4}}+P\frac{\partial^{2}w}{\partial x^{2}}+\rho A\frac{\partial^{2}w}{\partial t^{2}}=q\left( {x,t} \right)$
图1
${w}(x,t) \big|_{x=0} =\frac{\partial {w}(x,t)}{\partial x} \Bigg|_{x=0} =0\\ {EI\frac{\partial ^{2}{w}(x,t)}{\partial x^{2}}} \Bigg|_{x=L} =\\ \qquad \left[ {EI\frac{\partial ^{3}{w}(x,t)}{\partial x^{3}}+P\frac{\partial {w}(x,t)}{\partial x}} \right]_{x=L} =0$
1.1 横向位移
式(1)中去掉时间导数项,假设外激励与时间$t$无关,得横向弯曲的微分方程为
(2) $ EI\frac{\partial^{4}w_{\rm s} }{\partial x^{4}}+P\frac{\partial^{2}w_{\rm s} }{\partial x^{2}}=q_{\rm s} \left( x \right) $
式(2)中用$w_{\rm s}(x)$和$q_{\rm s}(x)$分别表示梁横向位移和静态横向分布载荷。假设
(3) $ w_{\rm s} (x)=\sum\limits_{j=1}^n {a_{j} } \phi_{j} (x) $
(4) $\hspace{-8mm}\phi_{j} (x)=\sin (\beta_{j} x)-\sinh (\beta_{j} x)-\\ \hspace{-8mm}\qquad \frac{\sin (\beta_{j} L)+\sinh (\beta_{j} L)}{\cos (\beta_{j} L)+\cosh (\beta_{j} L)}(\cos (\beta_{j} x)-\cosh (\beta_{j} x)) $
为满足位移边界的试函数,式(4)中$\beta_{j}$是超越方程$\cos (\beta_{j}L)\cosh (\beta_{j} L)+1=0$的根。式(3)代入到式(2),两边同乘$\phi_{i}(x)$ ($i = 1,2,\cdots,n$),并在 [0, $L$] 积分得到矩阵方程为
(5) $ {\widetilde{{K}}}_{n\times n} {\widetilde{{A}}}_{n\times 1} ={Q}_{n\times 1} $
(6) $\left.\begin{array}{l}\widetilde{K}_{i j}=\int_{0}^{L}\left(E I \phi_{i}^{\prime \prime \prime \prime}+P \phi_{i}^{\prime \prime}\right) \phi_{j} \mathrm{~d} x \\\widetilde{A}_{i 1}=a_{i}, \quad Q_{i 1}=\int_{0}^{L} q \phi_{i} \mathrm{~d} x\end{array}\right\}$
(7) $ \widetilde{A}_{n\times 1} =\widetilde{K}_{n\times n}^{-1}{Q}_{n\times 1} $
1.2 固有频率
略去式(1)中外激励项$q(x,t)$,并设$w(x,t)=W(x)\sin (\omega t+\phi )$ ($W(x)$为振型函数,$\omega $ 为系统的固有频率),得到
$EIW""+PW"-\rho A\omega^{2}W=0$
(9) $ W(x)=\sum\limits_{j=1}^n {{b}_{j} } \phi_{j} (x) $
其中,$b_{j}$ 为待定系数,$\phi_{j}$ ($x)$见式(4)。参照上述横向位移求解过程,得矩阵齐次方程为
(10) $ \left( {{\hat{{K}}}_{n\times n} -{\hat{{M}}}_{n\times n} \omega^{2}} \right){\hat{{A}}}_{n\times 1} ={\bf0} $
(11) $\left.\begin{array}{rl}\hat{K}_{i j} & =\int_{0}^{L}\left(E I \phi_{i}^{\prime \prime \prime \prime}+P \phi_{i}^{\prime \prime}\right) \phi_{j} \mathrm{~d} x \\\hat{M}_{i j} & =\rho A \int_{0}^{L} \phi_{i} \phi_{j} \mathrm{~d} x, \quad \hat{A}_{i 1}=b_{i}\end{array}\right\}$
为使式(10)有非平凡解,则令其系数矩阵的行列式为零,即
(12) $ \left| {{\hat{{K}}}_{n\times n} -{\hat{{M}}}_{n\times n} \omega^{2}} \right|=0 $
2 验证和讨论
考虑物理参数:$L= 1$ m,$EI=4.0$ MNm$^{2}$,$\rho A = 100$ kg/m[3 ] 。不失一般性,引入无量纲量
(13) $\left.\begin{array}{c}\xi=\frac{x}{L}, \quad \bar{w}_{\mathrm{s}}=\frac{w_{\mathrm{s}}}{L}, \bar{P}=\frac{P}{P_{\mathrm{cr}}} \\\bar{q}_{\mathrm{s}}=\frac{q_{\mathrm{s}} L^{3}}{E I}, \quad \bar{\omega}=\omega \sqrt{\frac{\rho A L^{4}}{E I}}\end{array}\right\}$
其中,$P_{\rm cr} = EI\pi^{2}/(4L^{2})$为悬臂梁临界屈曲载荷[4 ] ,为了使梁不发生屈曲失稳,应保证$\overline{{P}}<1$。
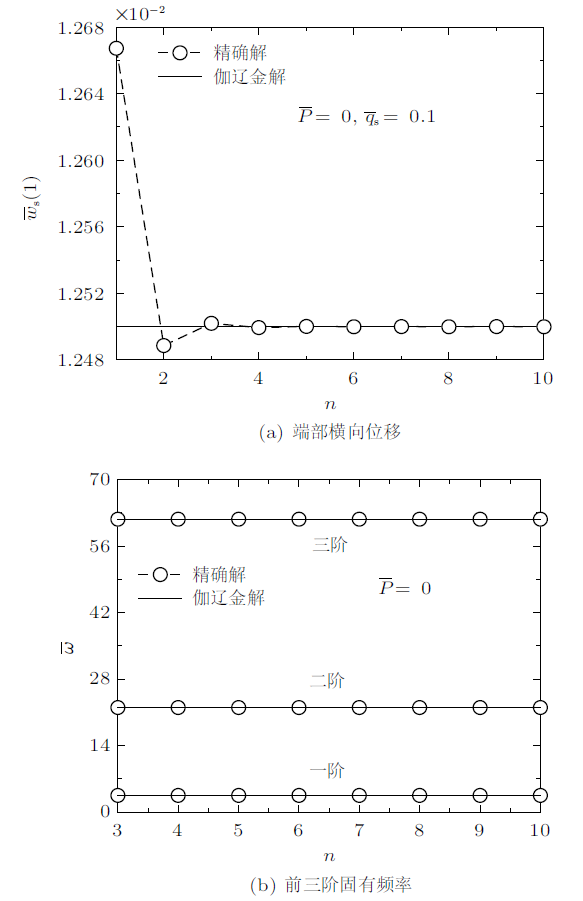
为检验伽辽金法的正确性和收敛性,图2 (a)和图2 (b)分别给出了$\overline{{P}} =0$时,试函数数目对悬臂梁端部横向位移和前三阶固有频率的影响。注意,悬臂梁($\overline{{P}}=0$)在均布载荷作用下横向位移及其固有频率的精确解已在材料力学和振动力学教材给出。可见随着试函数数目增加,悬臂梁端部横向位移和固有频率的伽辽金解迅速收敛于精确解。值得指出的是,由于$\overline{{P}}=0$,此时伽辽金的试函数(式(4))同时满足悬臂梁的位移和力边界条件,因此随着试函数数目的增加,伽辽金解收敛于精确解。为减小试函数数目的影响,下面计算皆取n=10。
图2
图2
悬臂梁横向位移的解析解与不同试函数个数下的伽辽金解比较
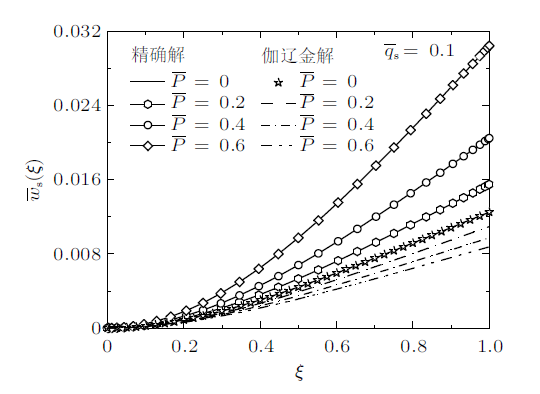
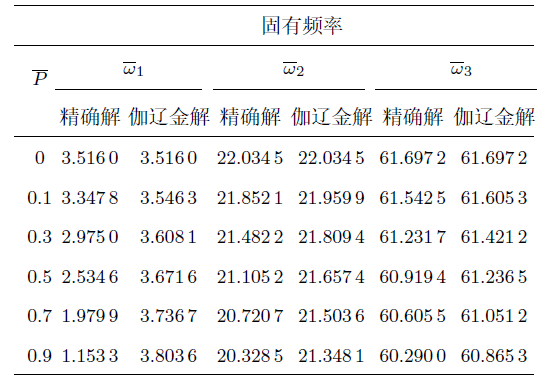
下面分析试函数(式(4))仅满足位移边界条件时(右端部不满足剪力边界条件),伽辽金法求解轴力作用下悬臂梁的横向位移和固有频率的正确性。图3 给出了不同轴向压力下悬臂梁横向位移的精确解和伽辽金解,其中悬臂梁横向位移的精确解采用格林函数法求得,具体计算见文献[4 ] 。可见随着轴向压力的增加,横向位移的精确解逐渐增大,该结果是预料之中的,因为轴向压力使梁软化增加其位移;然而横向位移的伽辽金解竟呈现截然相反的趋势,它表明轴向压力使梁硬化减小其位移,显然这个结论是错误的。进一步,表1 给出了不同轴压下悬臂梁前三阶固有频率。从表中可见,随着轴向压力增大,前三阶固有频率的精确解减小,一阶固有频率变化最为剧烈,而一阶固有频率的伽辽金解增加,二、三阶固有频率仅微弱减小,再次得到错误的结果。
图3
3 结论
本文通过采用伽辽金法计算轴向力下悬臂梁的横向位移和固有频率为例,得出仅选取满足位移边界条件的试函数,伽辽金法可能无法获得正确的结论。鉴于此,建议应用伽辽金法选取的试函数应严格满足结构的位移和力边界条件。
参考文献
View Option
[1]
曾攀 . 有限元分析及应用 . 北京 : 清华大学出版社 , 2004
[本文引用: 1]
[2]
高淑英 , 沈火明 . 振动力学 . 北京 : 中国铁道出版社 , 2011
[本文引用: 1]
[3]
Han F Dan D Cheng W . Exact dynamic characteristic analysis of a double-beam system interconnected by a viscoelastic layer
Composites Part B$:$ Engineering 2019 , 163 :272 -281
[本文引用: 1]
[4]
Li XY Wang XH Chen YY , et al . Bending, buckling and free vibration of an axially loaded timoshenko beam with transition parameter: direction of axial force
Int J Mech Sci. 2020 , 176 :1055 45
[本文引用: 2]
1
2004
... 伽辽金法类属于加权残值法,在《有限元方法》和《计算结构力学》教科书中都会讲授[1 -2 ] .该方法在具体应用时会涉及试函数的选取,通常要求试函数为一组线性无关的函数,并满足结构的所有位移和力边界条件.一些文献指出在难于选取满足所有边界条件的试函数时,可以选取仅满足位移边界条件不必满足力边界条件的试函数,通过增加试函数的个数弥补不满足力边界条件引起的误差.然而,这种简化与加权残值法的基本原理相违背,获得结果可能无法收敛于正确解.下面以计算同时受轴向力和横向分布力悬臂梁的横向位移和固有频率为例进行说明. ...
1
2011
... 伽辽金法类属于加权残值法,在《有限元方法》和《计算结构力学》教科书中都会讲授[1 -2 ] .该方法在具体应用时会涉及试函数的选取,通常要求试函数为一组线性无关的函数,并满足结构的所有位移和力边界条件.一些文献指出在难于选取满足所有边界条件的试函数时,可以选取仅满足位移边界条件不必满足力边界条件的试函数,通过增加试函数的个数弥补不满足力边界条件引起的误差.然而,这种简化与加权残值法的基本原理相违背,获得结果可能无法收敛于正确解.下面以计算同时受轴向力和横向分布力悬臂梁的横向位移和固有频率为例进行说明. ...
Exact dynamic characteristic analysis of a double-beam system interconnected by a viscoelastic layer
1
2019
... 考虑物理参数:$L= 1$ m,$EI=4.0$ MNm$^{2}$,$\rho A = 100$ kg/m[3 ] .不失一般性,引入无量纲量 ...
Bending, buckling and free vibration of an axially loaded timoshenko beam with transition parameter: direction of axial force
2
2020
... 其中,$P_{\rm cr} = EI\pi^{2}/(4L^{2})$为悬臂梁临界屈曲载荷[4 ] ,为了使梁不发生屈曲失稳,应保证$\overline{{P}}<1$. ...
... 下面分析试函数(式(4))仅满足位移边界条件时(右端部不满足剪力边界条件),伽辽金法求解轴力作用下悬臂梁的横向位移和固有频率的正确性.图3 给出了不同轴向压力下悬臂梁横向位移的精确解和伽辽金解,其中悬臂梁横向位移的精确解采用格林函数法求得,具体计算见文献[4 ] .可见随着轴向压力的增加,横向位移的精确解逐渐增大,该结果是预料之中的,因为轴向压力使梁软化增加其位移;然而横向位移的伽辽金解竟呈现截然相反的趋势,它表明轴向压力使梁硬化减小其位移,显然这个结论是错误的.进一步,表1 给出了不同轴压下悬臂梁前三阶固有频率.从表中可见,随着轴向压力增大,前三阶固有频率的精确解减小,一阶固有频率变化最为剧烈,而一阶固有频率的伽辽金解增加,二、三阶固有频率仅微弱减小,再次得到错误的结果. ...