作为一种计算位移的一般性方法,基于变形体虚功原理的单位载荷法是材料力学的重点教学内容,甚至静不定问题、对称/反对称问题、冲击问题都可以视为单位载荷法的应用。

变形体虚功原理常表述为虚力原理与虚位移原理两种模式,在材料力学教学内容中,克罗蒂-恩盖塞定理(Crotti-Engesser)、卡氏第二定理(Castigliano)、单位载荷法(unit-load)的推导基于虚力原理;卡氏第一定理的推导基于虚位移原理。但多数材料力学教科书(包括工程力学教材中材料力学部分)中不涉及余功和余能概念^[1-3],或者新版教材中删去余功和余能的部分^[4],造成与虚力原理相关的余虚功(包括内余虚功和外余虚功)无法引入,后续也就不能基于虚力原理推导以上定理和方法。目前大部分教材的处理方案是：删去克罗蒂–恩盖塞定理,适用于线弹性条件的卡氏第二定理使用交换加载次序或引用功的互等定理加以证明,而单位载荷法使用虚位移原理的相关概念进行描述(孙训方的教材^[5]保留了余功余能部分,但单位载荷法仍使用虚位移原理的模式引入)。

这种使用虚位移原理讲授单位载荷法的间接模式,加上虚位移定义的限制,导致讲授中的重点(也是后续例题讲解中的难点)是：以实际载荷引起的位移作为单位力系统的虚位移^[1-2,4-5]。对该问题的理解与延拓不仅涉及单位载荷系统的选取与构造,还决定了学生使用单位载荷法解决问题的灵活性,为此本文利用教材中经典例题展示其中的细节与关联,供教师讲解时参考。

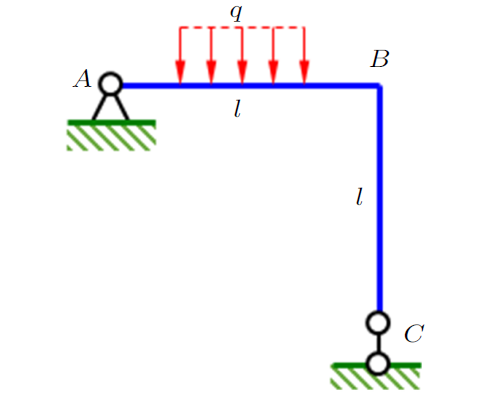
变形体虚功原理可表述为^[4]：作用在杆或杆系结构的外力在虚位移上所做外虚功$W_{{\rm e}}$,恒等于可能内力在虚变形上所做内虚功$W_{{\rm i}} $,即$W_{{\rm e}}=W_{{\rm i}} $。很明显,以上表述是典型虚位移模式。

应用虚功原理的条件：

(1) 对于所研究的力系(外力与内力)必须满足平衡条件与静力边界条件;

(2) 对于所选择的虚位移是微小的,满足变形连续条件与位移边界条件。

在虚位移模式的单位载荷法表述中：满足位移边界条件与变形连续条件的任意微小位移,均可作为虚位移。因此,由实际载荷引起的位移也可作为虚位移。

为了方便后续问题的讨论,此处使用图1以及对应单位载荷系统的图2作为范例。为了求出图1中$B$点转角,在$B$点施加单位力矩构造了单位载荷系统(图2)。

利用图1的实际位移作为图2单位载荷系统的虚位移,单位载荷系统对应的虚功方程为(注：本文实例中结构材料满足线弹性假设,忽略剪切与拉压应变能)

式中$M\left( {x_{i} } \right)$与$\overline{{M}}\left( {x_{i} }\right)$分别为原始系统(图1)与单位载荷系统(图2)各段梁内的弯矩方程(在本文中由单位载荷引入的约束外力与内力均采用符号上方的横线表征)。

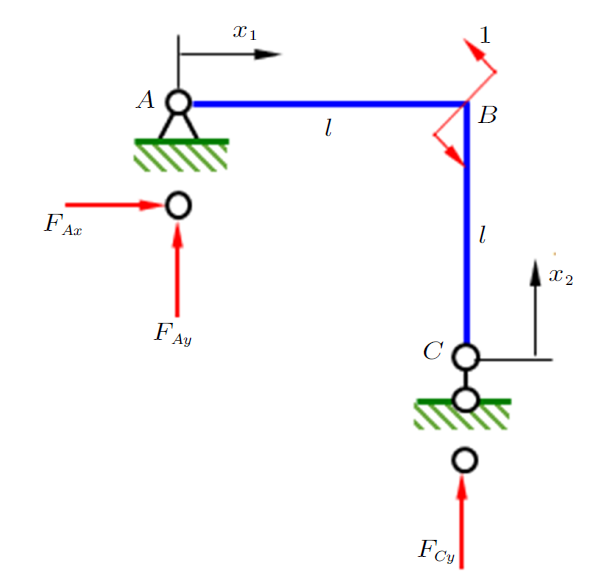
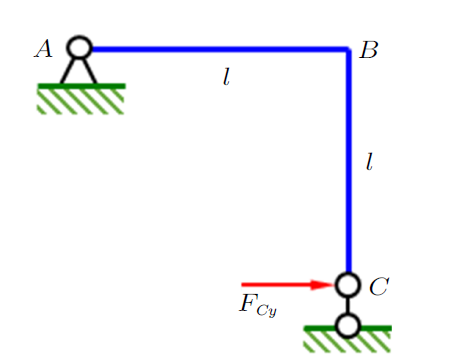
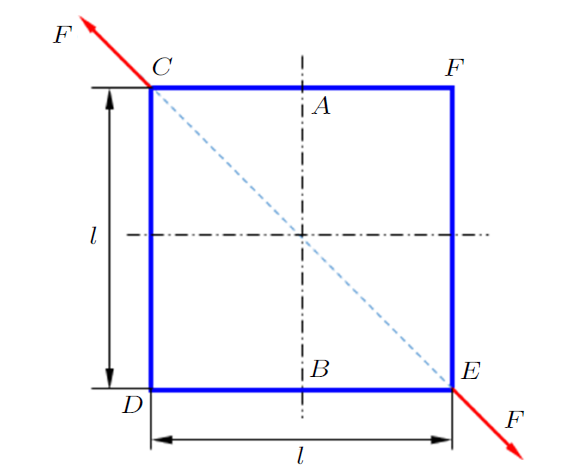
此处详细列出虚功方程的目的是为了说明：理论上,式(1)左侧的外力虚功除单位载荷引起的$1\times\theta_{{B}}$外,还包含$A$点与$C$点的约束反力引入的外力虚功$\overline{F}_{Ax} \times H_{A}+\overline{F}_{Ay} \times V_{A} +\overline{F}_{Cy} \times V_{C}$,这几项未在虚功方程中出现的原因是$H_{A} =V_{A} =V_{C} =0$,$H_{i}$与$V_{i} $分别表示$i$点的水平与垂直位移。

可以看出,此处要求虚位移满足边界条件等价于除单位载荷所引入的外力虚功外,其他所有与单位载荷相关的约束反力造成的外力虚功为零。

对于上述静定结构,单位载荷系统的构造具有简单性和唯一性。当使用单位载荷法求解静不定结构某点位移时,可以使用静不定结构的任一静定基构造单位载荷系统。以图3静不定结构为例,同样求解$B$点的转角,按照前节的方法构造的单位载荷系统应为图4所示,但需要重复求解静不定问题,造成计算繁琐。一种解决的方案是将单位载荷施加于原结构的任一静定基上(例如图2),课堂讲解的重点在于为什么可以采用结构的任一静定基构造单位载荷系统。

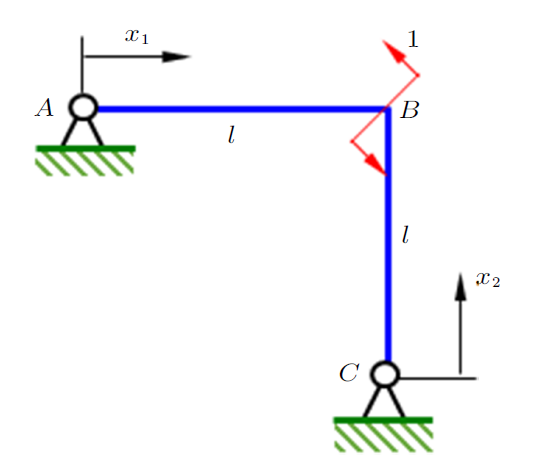
由于教材中单位载荷法基于虚位移模式,按照虚位移的定义,问题转化为：实际载荷下的位移(真实位移)是否可以作为基于静不定结构任一静定基构造的单位载荷系统的虚位移?

图3中实际位移一定可以作为图4中单位载荷系统的虚位移,因为二者边界条件完全一致。尽管图2 (静不定结构某一静定基构造的单位载荷系统)所示系统的边界条件与原始结构不同,但其一定弱于原始系统,具体而言如下。

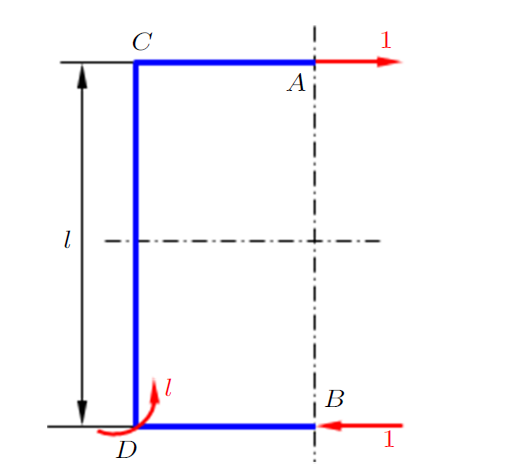
图2所示系统要求的虚位移满足

$A$点：水平位移$H_{A} =0$,垂直位移$V_{A} =0$,

$C$点：垂直位移$V_{C} =0$;

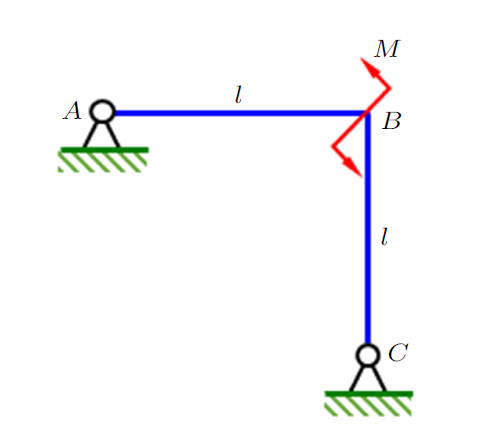
实际载荷下(图3所示原始系统)的位移满足

$A$点：水平位移$H_{A} =0$,垂直位移$V_{A} =0$,

$C$点：水平位移$H_{C} =0$,垂直位移$V_{C} =0$;

即静不定结构在实际载荷下的位移可以作为任一静定基单位载荷系统的虚位移,原因在于静不定结构的边界条件多于其任一静定基的位移边界条件,所以前者位移解的集合是后者的子集。

针对该问题,单辉祖^[6]编写的教学参考书中给出了一个详细证明,其基本思路是基于原始静不定结构的单位载荷系统(图4)可以分解为图2与图5两部分,可以证明图5所对应的内力虚功为零,因此图4与图2的内力虚功相等,进而证明了采用基于静定基求解位移(图2)等价于在原始静不定结构上施加单位载荷(图4)求解位移。

事实上,无需复杂公式推导过程,以实际载荷下的位移作为虚位移时,图5所对应的内力虚功为零是显而易见的：$F_{Cy}$对应的外力虚功一定等于零,因为$C$点实际的水平位移为零(当然,其他由$F_{Cy}$引入的约束反力所对应的外力虚功也为零),所以图5对应的内力虚功必定为零。

相对于简单直观的静定结构,阐述静不定结构单位载荷系统构造可以基于任一静定基的机理,关键在于说明静不定结构与其静定基在边界条件上的关系,即静不定结构的边界条件"强"于其任一静定基,所以静不定结构的位移可以作为其任一静定基的虚位移,但反之不成立。

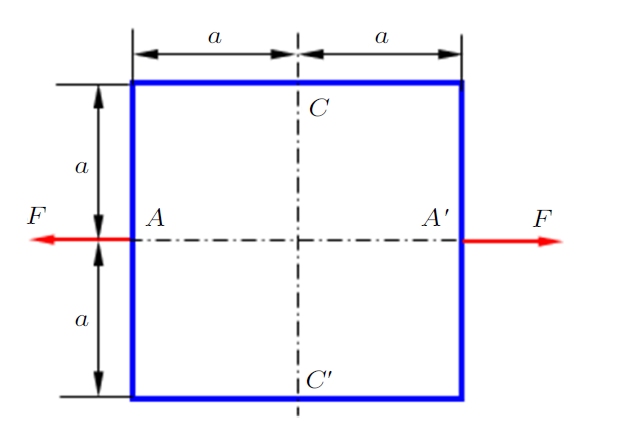
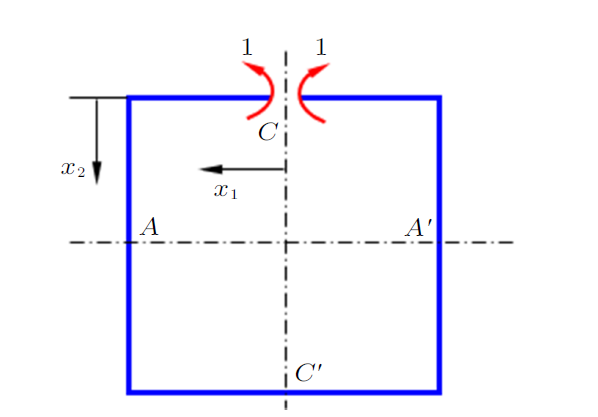
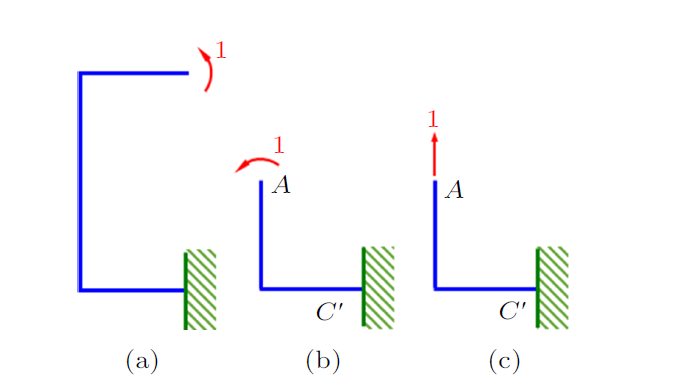
利用对称性简化静不定问题的分析在材料力学课程中归属于能量法的应用,其中典型例题讲解的难点在于无约束条件下对于部分结构的单位载荷系统的构造,例如图6所示的对称问题。除利用相对位移协调条件的整体结构单位载荷系统(例如图7)外,常常使用1/2结构(图8(a))或1/4结构(图8(b))构造单位载荷系统,可利用对称面处绝对位移条件。与第2节中论述不同,此时实际位移(图6的真实位移)并不严格满足图8中单位载荷系统的边界条件($V_{C'}=0$),即实际位移中${C}'$点垂直方向的位移不为零,如果根据前述虚位移的描述,实际位移不能作为图8单位载荷系统的虚位移,此处基于虚位移的单位载荷法是否可用成为需要说明的问题。

如果前期采用虚力模式导入单位载荷法,这个问题容易解释,为了避免余功与余虚功的引入,采用虚位移模式导入单位载荷法,此时该问题就成为一个难点。尽管在教材的例题中已经避免出现类似图8的单位载荷系统,但在网上众多材料力学教案、各类习题解答、教学参考书和考研教辅资料中采用部分结构构造单位载荷系统是主流,这对于认真思考的学生将造成困惑。

理论上,满足位移边界条件只是虚位移定义中的限制条件,并不是虚功原理的要求：虚功原理中的力与位移(变形)并无直接或因果关联,力的要求是平衡,位移的要求是位移与变形对应协调,在此基础上外力虚功等于内力虚功。换言之,实际位移不满足单位载荷系统的位移边界条件,并不影响虚功方程的成立,但是该虚功方程是否有作用(是否可以解算获得待求位移)取决于单位载荷系统的构造。下面仍用上例列出具体表达式,以实际位移(图6)作为部分结构构造的单位载荷系统的虚位移(图8(a)),外力虚功为(内力虚功不再列出)

其中$\overline{{M}}_{{C}'} $,$\overline{{F}}_{{\rm N}{C}'}$,$\overline{{F}}_{{\rm S}{C}'}$分别为图8(a)中由$C$点单位力矩引入在${C}'$点的约束反力,$\theta_{{C}'}$,$H_{{C}'} $,$V_{{C}'} $分别为图6结构中${C}'$点的实际位移。尽管$V_{{C}'}\ne 0$并不满足单位载荷系统的位移边界条件,但并不影响虚功方程的成立。进一步,如果外力虚功中除了$1\times\theta_{C}$以外还有其他项不为零,则该虚功方程没有作用(不能利用$C$点的已知位移求解静不定问题)。

对于图8(a)单位载荷系统的构造,由于$C$点施加单位力矩,所以在${C}'$点的$\overline{{F}}_{{\rm S}{C}'}$为零,尽管$V_{{C}'} \ne 0$,但$\overline{{F}}_{{\rm S}{C}'} \times V_{{C}'}=0$,保证了$W_{{\rm e}} =1\times \theta_{C}$,所以这种单位载荷系统的构造是可用的,图8(b)的1/4结构单位载荷系统构造也是同样的机理。但是图8(c)对应的单位载荷系统不可用,原因在于尽管虚功方程仍可列出,但$\overline{{F}}_{{\rm S}{C}'}\ne 0$,导致$\overline{{F}}_{{\rm S}{C}'} \times V_{{C}'} \ne0$,此时$W_{{\rm e}} =1\times V_{A} +\overline{{F}}_{{\rm S}{C}'} \times V_{{C}'} $,不能利用$A$点的已知位移$V_{A} $求解静不定问题。

以上的实例说明,实际位移满足单位载荷系统的边界条件并不是虚功原理的要求,只是为了保证虚功方程对于实际问题解算有用而设定的条件。如果实际位移完全满足单位载荷系统的边界条件,则对于构造单位载荷系统所施加单位载荷的类型没有任何限制条件,否则需注意,施加单位载荷不能引入不满足位移边界条件的位移所对应的约束力分量。

在对称性问题中,除此类构造固定边界模式外,还有一大类构造非固定边界单位载荷系统的问题^[7],其机理类似。例如图9所示结构,求解$A$点与$B$点相对水平位移,采用了图10所示1/2结构构造单位载荷系统,为了保证该自由边界结构的力平衡,需要施加大小为$l$的力矩。

图10中该力矩可以施加的位置在$D$点(或$C$点),其原因在于：这两点的转角为零(图9中的实际位移),这就保证了外力虚功中仅出现$1\times H_{{A/B}} $。

基于虚功原理的单位载荷法在能量方法中占据重要地位,材料力学教学中静不定问题、对称反对称问题以及冲击问题在某种程度上可以看作单位载荷法的应用外延。

大部分经典教材对于单位载荷法使用虚位移模式引入,讲解过程不可避免涉及虚位移须满足位移边界条件的限制,深刻理解单位载荷系统构造的本质有助于灵活处理该限制条件。本文通过几个经典例题(包括静定结构、静不定结构、无约束的静不定结构),展示了虚功原理中力与位移(变形)并无直接关联,使用实际位移作为单位载荷系统的虚位移时,要求虚位移满足单位载荷系统边界条件的目的,只是为了保证除单位载荷的外力虚功外,其他由约束力造成的外力虚功全部为零。所以,只要能保证约束反力的外力虚功均为零,实际位移作为单位载荷系统的虚位移,并不要求其完全满足单位载荷系统的边界条件。