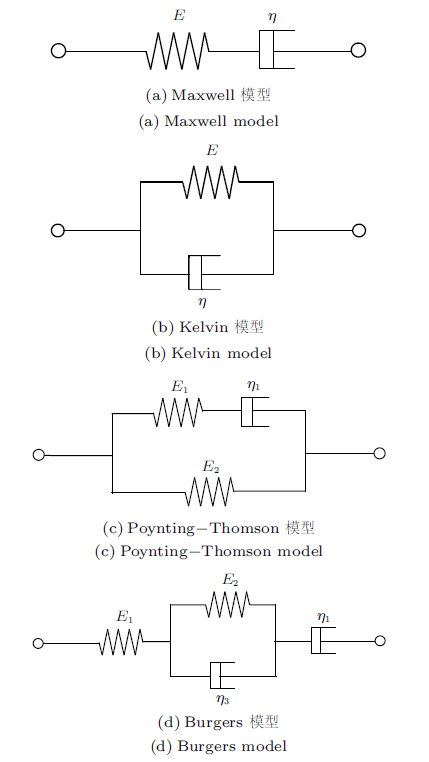
黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举。由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义。材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一。为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟。如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等。多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] 。利用这些模型,诸多学者在各个工程领域开展了大量的研究。例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征。范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究。Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征。Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为。为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] 。候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应。李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程。詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究。潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解。不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] 。一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] 。但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础。图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式。并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式。该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义。
图1
1 本构方程的矩阵形式表述
一般的黏弹性力学教材中都给出了各种基本模型的微分型本构方程[14 ] ,如:Maxwell模型、Kelvin模型、Poynting-Thomson模型、Burgers模型等等。由于弹性元件和黏性元件数量不多,它们的本构方程推导过程并不难。为了实现计算机编程计算本构方程,以下利用图论算法和矩阵运算,通过推导由10个弹性元件和黏性元件构成的较为复杂模型的应力-应变微分关系,总结和建立任意线性黏弹性模型的微分型本构方程的一般形式。
如图2 (a)所示的10元件黏弹性模型,可以看成由Maxwell单元连接组成,如图2 (b)中所示。单个Maxwell单元的应力-应变微分关系为
(1) $\dfrac{\dot{{\sigma }}}{E}+\dfrac{\sigma }{\eta }=\dot{{\varepsilon }}$
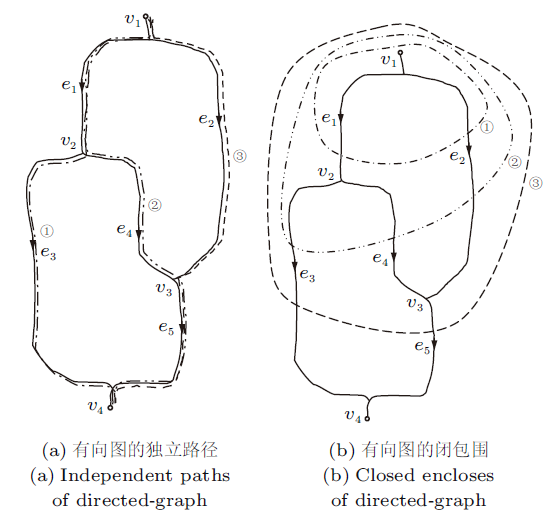
图2
基于公式(1),只要写出10元件黏弹性模型的应变$\varepsilon$、模型的应力$\sigma $与各个Maxwell单元的应变$\varepsilon_{i}$ ($i=1,2,\cdots,5$),应力$\sigma_{i}$ ($i=1,2,\cdots,5$)之间的关系式,将它们适当求导,并写成矩阵形式,模型的微分型本构方程即可以通过各系数矩阵的运算得到。为了计算便捷和程式化,借助图论中有向图的相关工具,可迅速将求解过程编写成程序。现将整个求解过程描述如下。
(1) 根据黏弹性模型中的弹簧和阻尼器的连接方式,写出模型的总应变$\varepsilon$与各个Maxwell单元的应变$\varepsilon_{i}$之间的关系式,并求$j$阶导数。将模型的总应变$\varepsilon$及其导数与各Maxwell单元的应变$\varepsilon_{i}$及其导数的关系式以矩阵形式记为
(2) $I_{r,j+1} {D}^{j}\varepsilon ={A}\times {D}^{j}\varepsilon_{i}$
式中,记${D}^{j}\varepsilon $表示由模型的总应变$\varepsilon$及其1~$j$阶导数组成的列向量,有$j+1$个元素,形如式(3)所示
(3) ${D}^{j}\varepsilon =\left[\varepsilon {\dot{{\varepsilon }}} \cdots {\dfrac{{\rm d}^{j}\varepsilon }{{\rm d}t^{j}}}\right]^{\rm T}$
记${D}^{j}\varepsilon_{i} $表示各个Maxwell单元的应变$\varepsilon_{i}$及其1~$j$阶导数组成的列向量,有$i\times(j+1)$个元素,$i$为Maxwell单元的数量,形如式(4)所示
(4) ${D}^{j}\varepsilon_{i} =\\\quad \bigg[ {\varepsilon_{1} } {\varepsilon_{2} } \cdots {\varepsilon_{i} } {\dot{{\varepsilon }}_{1} } {\dot{{\varepsilon }}_{2} }\cdots {\dot{{\varepsilon }}_{i} } \\\quad {\dfrac{{\rm d}^{j}\varepsilon_{1} }{{\rm d}t^{j}}} {\dfrac{{\rm d}^{j}\varepsilon_{2} }{{\rm d}t^{j}}} \cdots {\dfrac{{\rm d}^{j}\varepsilon_{i} }{{\rm d}t^{j}}}\bigg]^{\rm T}\\\quad$
系数矩阵$A$有$(j+1)\times r$行,$i\times (j+1)$列,为行满秩矩阵,即$R({A})=(j+1)r$。${I}_{r,j+1} $是形如式(5)所示的矩阵。因模型的总应变$\varepsilon$与各个Maxwell单元的应变$\varepsilon _{i}$之间的关系式共有$r$个独立方程,故乘以该${I}_{r,j+1}$矩阵来将其合写成一个矩阵方程。
(5) $\boldsymbol{I}_{r, j+1}=\underbrace{\left[\begin{array}{cccc}\boldsymbol{d}_{r} & \mathbf{0} & \cdots & \mathbf{0} \\\mathbf{0} & \boldsymbol{d}_{r} & \cdots & \mathbf{0} \\\cdots & \cdots & \cdots & \cdots \\\mathbf{0} & \mathbf{0} & \cdots & \boldsymbol{d}_{r}\end{array}\right]}_{j+1}\}_{j+1}^{[}$
式中,${d}_{r}$为共有$r$个元素且值全为1的向量。将模型转化为有向图,如图3 所示。模型的总应变$\varepsilon$与各个基础元件的应变$\varepsilon_{i}$之间的$r$个独立应变关系式可以根据由Maxwell单元组成的模型中由起点到终点的独立路径的数量进行确定。有向图中独立路径的数量即为$r$,如图3 (a)中所示,$r=3$。可以写出3个总应变$\varepsilon$与各个Maxwell单元的应变$\varepsilon_{i}$之间的关系式,即
(6) $\varepsilon =\varepsilon_{1} +\varepsilon_{3}\\$
(7) $\varepsilon =\varepsilon_{1} +\varepsilon_{4} +\varepsilon_{5}\\$
(8) $\varepsilon =\varepsilon_{2} +\varepsilon_{5}$
图3
根据图论中求解有向图路径的方法,先写出图的关联矩阵为
(9) $\boldsymbol{M}=\left[\begin{array}{ccccc}e_{1} & e_{2} & e_{3} & e_{4} & e_{5} \\1 & 1 & 0 & 0 & 0 \\-1 & 0 & 1 & 1 & 0 \\0 & -1 & 0 & -1 & 1 \\0 & 0 & -1 & 0 & -1\end{array}\right] \begin{array}{l}v_{1} \\v_{2} \\v_{3} \\v_{4}\end{array}$
列出方程$Mx=b$,然后求其解($x$的元素只能是1或者0,向量$b$表示从起点$v_{1}$到终点$v_{4})$。
(10) $\left[\begin{array}{ccccc}1 & 1 & 0 & 0 & 0 \\-1 & 0 & 1 & 1 & 0 \\0 & -1 & 0 & -1 & 1 \\0 & 0 & -1 & 0 & -1\end{array}\right] \cdot \boldsymbol{x}=\left[\begin{array}{c}1 \\0 \\0 \\-1\end{array}\right] \begin{array}{l}v_{1} \\v_{2} \\v_{3} \\v_{4}\end{array}$
方程(10)的满足条件的解中,有3个线性无关的解向量为
(11) $\boldsymbol{x}_{1}=\left[\begin{array}{l}1 \\0 \\1 \\0 \\0\end{array}\right], \quad x_{2}=\left[\begin{array}{l}1 \\0 \\0 \\1 \\1\end{array}\right], \quad x_{3}=\left[\begin{array}{l}0 \\1 \\0 \\0 \\1\end{array}\right]$
以式(11)中的每一个解表示一条从起点$v_{1}$到终点$v_{4}$的路径,解的第几个元素为1表示该路径经过第几条有向边。如:向量$\bm
x_{2}$的第1,4,5行元素为1,其余元素为0,表示图3 (a)中路径②是一条经过$e_{1}$,$e_{4}$,$e_{5}$从起点$v_{1}$到终点$v_{4}$的路径。由$x_{1}$,$x_{2}$,$x_{3}$构成的矩阵即为独立路径矩阵,记为$R$。
(12) $\boldsymbol{R}=\left[\begin{array}{lll}\boldsymbol{x}_{1} & \boldsymbol{x}_{2} & \boldsymbol{x}_{3}\end{array}\right]^{\mathrm{T}}=\left[\begin{array}{ccccc}1 & 0 & 1 & 0 & 0 \\1 & 0 & 0 & 1 & 1 \\0 & 1 & 0 & 0 & 1\end{array}\right]$
对比式(2)~式(8),式(12),可以得出式(2)中的矩阵$A$可由独立路径矩阵$R$构造而成。
(13) $A=\underbrace{\left[\begin{array}{cccc}R & 0 & \cdots & 0 \\0 & R & \cdots & 0 \\\cdots & \cdots & \cdots & \cdots \\0 & 0 & \cdots & R\end{array}\right]}_{j+1}\} j+1$
(2) 根据黏弹性模型中的弹簧和阻尼器的连接方式,写出模型的总应力$\sigma$与各个Maxwell单元的应力$\sigma_{i}$之间的关系式,并求$m$阶导数,将模型的总应力$\sigma$及其导数与各Maxwell单元的应力$\sigma_{i}$及其导数的关系式以矩阵形式记为
(14) ${I}_{n,m+1} {D}^{m}\sigma ={B}\times {D}^{m}\sigma_{i}$
式中,模型的总应力$\sigma $与各个基础元件的应力$\sigma_{i}$之间的关系式共有$n$个独立方程,利用乘以${I}_{n,m+1}$来将其合写成一个矩阵方程。记${D}^{m}\sigma$表示由模型的总应力$\sigma$及其1~$m$阶导数组成的列向量,有$m+1$个元素,形如式(15)所示。
(15) $D^{m} \sigma=\left[\begin{array}{cccc}\sigma & \dot{\sigma} & \cdots & \frac{\mathrm{d}^{m} \sigma}{\mathrm{d} t^{m}}\end{array}\right]^{\mathrm{T}}$
记${D}^{m}\sigma_{i} $表示各个Maxwell单元的应力$\sigma_{i}$及其1~$m$阶导数组成的列向量,有$i\times(m+1)$个元素,$i$为Maxwell单元的数量,形如式(16)所示。
(16) $\begin{array}{l}\boldsymbol{D}^{m} \sigma_{i}= \\{\left[\begin{array}{llllllll}\sigma_{1} \sigma_{2} \cdots \sigma_{i} \dot{\sigma}_{1} \dot{\sigma}_{2} \cdots \dot{\sigma}_{i} \\\frac{\mathrm{d}^{m} \sigma_{1}}{\mathrm{~d} t^{m}} \frac{\mathrm{d}^{m} \sigma_{2}}{\mathrm{~d} t^{m}} \cdots \frac{\mathrm{d}^{m} \sigma_{i}}{\mathrm{~d} t^{m}}\end{array}\right]^{\mathrm{T}}}\end{array}$
系数矩阵$B$有$(m+1)\times n$行,$i\times (m+1)$列,为行满秩矩阵,即$R({B})=(m+1)n$。模型的总应力$\sigma$与各个基础元件的应力$\sigma_{i}$之间的$n$个独立关系式可以根据有向图中包含起点$v_{1}$的闭包围的数量进行确定(其中闭包围须满足条件:与闭包围相交的有向边的方向应指向外)。如图3 (b)中所示,$n=3$。可以写出3个总应力$\sigma$与各个Maxwell单元的应力$\sigma_{i}$之间的应力关系式,即
(17) $\sigma =\sigma_{1} +\sigma_{2}$
(18) $\sigma =\sigma_{2} +\sigma_{3} +\sigma_{4}$
(19) $\sigma =\sigma_{3} +\sigma_{5}$
因为有向图的任一闭包围必与每一条路径相交,故闭包围矩阵的任一行与独立路径矩阵$R$的每一行求点积必为1,于是闭包围矩阵可通过求方程$Rx=c$的解获得(非齐次项$c$为全1向量,其行数与$R$的行数相同,解$x$的元素只能是1或者0)。
(20) $\left[\begin{array}{lllll}1 0 1 0 0 \\1 0 0 1 1 \\0 1 0 0 1\end{array}\right] \cdot \boldsymbol{x}=\left[\begin{array}{l}1 \\1 \\1\end{array}\right]$
方程(20)的满足条件的解中,有3个线性无关的解向量为
(21) $\boldsymbol{x}_{1}=\left[\begin{array}{l}1 \\1 \\0 \\0 \\0\end{array}\right], \quad \boldsymbol{x}_{2}=\left[\begin{array}{l}0 \\1 \\1 \\1 \\0\end{array}\right], \quad \boldsymbol{x}_{3}=\left[\begin{array}{l}0 \\0 \\1 \\0 \\1\end{array}\right]$
以上式(21)中的每一个解表示有向图中一条包含起点$v_{1}$的闭包围,解的第几个元素为1表示该闭包围与第几条有向边相交。如:向量$x_{2}$的第2,3,4行元素为1,表示图3 (b)中闭包围②与有向边$e_{2}$,$e_{3}$,$e_{4}$相交。由以上解$x_{1}$,$x_{2}$,$x_{3}$构成的矩阵即为闭包围矩阵,记为$E$。
(22) $\boldsymbol{E}=\left[\begin{array}{lll}\boldsymbol{x}_{1} \boldsymbol{x}_{2} \boldsymbol{x}_{3}\end{array}\right]^{\mathrm{T}}=\left[\begin{array}{lllll}1 1 0 0 0 \\0 1 1 1 0 \\0 0 1 0 1\end{array}\right]$
对比式(14)~式(19),式(22),可以得出式(14)中的矩阵$B$可由闭包围矩阵$E$构造而成。
(23) $B=\underbrace{\left[\begin{array}{cccc}\boldsymbol{E} \mathbf{0} \cdots 0 \\\mathbf{0} \boldsymbol{E} \cdots 0 \\\cdots \cdots \cdots \cdots \\0 0 \cdots \boldsymbol{E}\end{array}\right]}_{m+1}\} m+1$
(3) 将Maxwell单元的应力-应变微分关系式(1)求适当阶数的导数后代入式(2),可得到模型的总应变$\varepsilon$与各个Maxwell单元的应力$\sigma_{i}$之间的关系式,以矩阵形式记为
(24) ${I}_{r,j+1} {D}^{j}{\varepsilon }'={H}\times {D}^{j+1}\sigma_{i}$
式中,记${D}^{j}{\varepsilon}'$表示对向量${D}^{j}\varepsilon$再求一阶导数,故${D}^{j}{\varepsilon}'$是由模型的总应变$\varepsilon$的1~$j+$1阶导数组成的列向量,有$j+$1个元素,形如式(25)所示。
(25) $\boldsymbol{D}^{j} \varepsilon^{\prime}=\left[\begin{array}{cccc}\dot{\varepsilon} & \ddot{\varepsilon} & \cdots & \frac{\mathrm{d}^{j+1} \varepsilon}{\mathrm{d} t^{j+1}}\end{array}\right]^{\mathrm{T}}$
由黏弹性模型中各弹簧的弹性模量$E_{i}$及各阻尼器的黏度系数$\eta_{i}$构造$Y$矩阵和$V$矩阵分别为
(26) $\boldsymbol{Y}=\underbrace{\left[\begin{array}{cccc}E_{1} & 0 & \cdots & 0 \\0 & E_{2} & \cdots & 0 \\\cdots & \cdots & \cdots & \cdots \\0 & 0 & \cdots & E_{i}\end{array}\right]}_{i}\} i$
(27) $\boldsymbol{V}=\underbrace{\left[\begin{array}{cccc}\eta_{1} & 0 & \cdots & 0 \\0 & \eta_{2} & \cdots & 0 \\\cdots & \cdots & \cdots & \cdots \\0 & 0 & \cdots & \eta_{i}\end{array}\right]}_{i}\} i$
(28) $\boldsymbol{H}=\underbrace{\left[\begin{array}{ccccc}\boldsymbol{R} \boldsymbol{V}^{-1} \boldsymbol{R} \boldsymbol{Y}^{-1} \ldots 0 0 \\0 \boldsymbol{R} \boldsymbol{V}^{-1} \cdots 0 0 \\\cdots \cdots \cdots \cdots \cdots \\0 \mathbf{0} \cdots \boldsymbol{R} \boldsymbol{V}^{-1} \boldsymbol{R} \boldsymbol{Y}^{-1}\end{array}\right]}_{j+2}\} j+1$
(4) 联立求解方程(14)与(24),消去中间变量${D}^{m}\sigma_{i}$,即可求得模型的应力$\sigma $与应变$\varepsilon$之间的微分关系式(需满足$m=j+1$,保证${D}^{m}\sigma_{i}={D}^{j+1}\sigma_{i} )$。具体求解过程如下。
将式(14)看成是非齐次线性方程组,将向量${D}^{m}\sigma_{i}$看成待求量,${I}_{n,m+1} {D}^{m}\sigma$为非齐次量,则${D}^{m}\sigma_{i} $可由${D}^{m}\sigma $表示为
(29) ${D}^{m}\sigma_{i} ={\rm null}({B})\times {k}+{P}$
式中,null($B$)表示矩阵$B$的零空间矩阵,$P$为式(14)的任意一特解,可按式(30)方法构造
(30) ${P}={F}\times {D}^{m}\sigma$
(31) $\boldsymbol{F}=\underbrace{\left[\begin{array}{cccc}\boldsymbol{f} 0 \cdots 0 \\0 \boldsymbol{f} \cdots 0 \\\cdots \cdots \cdots \cdots \\0 0 \cdots \boldsymbol{f}\end{array}\right]}_{m+1}\} m+1$
式中,列向量$f$可取独立路径矩阵$R$的任一行通过转置得到,$F$矩阵有$i\times (m+1)$行,$m+1$列。将式(29)代入式(24),可得
(32) ${I}_{r,j+1} {D}^{j}{\varepsilon }'={H}\times {\rm null}({B})\times {k}+{H}\times {P}$
(33) ${C}={H}\times {\rm null}({B})$
求出$C^{{\rm T}}$的零空间矩阵null($C^{{\rm T}})$。式(33)中,null($B$)为$i\times(m+1$)行,($i-n)\times (m+1)$列矩阵,$H$为$r\times(j+1)$行,$i\times (j+2)$列矩阵(因为$m=j+1$,${H}\times {\rm null}({B})$符合矩阵乘法规则)。$C$为$r\times (j+1)$行,$(i-n)\times (m+1)$列矩阵,故$C^{{\rm T}}$的零空间矩阵null($C^{{\rm T}})$有$r\times (j+1)$行,$r\times (j+1)-(i-n)\times (m+1)$列。记null($C^{{\rm T}})$的某一个列向量为$b$,将其转置并左乘式(32),则可以得到黏弹性模型的应力$\sigma $与应变$\varepsilon $之间的微分关系式的矩阵形式表述为
(34) ${b}^{\rm T}\times {I}_{r,j+1} \times {D}^{j}{\varepsilon }'={b}^{\rm T}\times {H}\times {F}\times {D}^{m}\sigma$
(5) 上述计算过程中,关于$r$个应变方程及$n$个应力方程求多少阶导数最合适的问题,即$m$和$j$的取值为多少合适。从上述的应变方程和应力方程以及推导过程可知,应力的求导阶数比应变应该高一阶,故应有$m=j+1$。为了使$C^{{\rm T}}$的零空间矩阵null($C^{{\rm T}})$至少含有一个向量$b$,则应有
(35) $(j+1)r-(i-n)(m+1)\geqslant 1$
解得$m\geqslant \dfrac{1-n+i}{n+r-i}$
式中,$i$为黏弹性模型中Maxwell单元的数量。
(6) 为了将上述计算方法程式化,需要将黏弹性模型中的所有弹性元件和黏性元件都配对成Maxwell基本单元。当由弹簧和阻尼器构成的连接图中存在有非Maxwell基本单元时,先把非Maxwell单元的部分扩展成Maxwell单元。例如,图1 (c)所示的Poynting-Thomson模型,可以通过添加相应的弹簧和阻尼器进行扩展成如图4 (a)所示,则该模型中的非Maxwell单元的部分都扩展成了Maxwell单元,如图4 (b)所示。先计算出图4 所示的黏弹性模型的微分本构方程,然后令$\eta_{2}$为$\infty $,即与原模型等价。
图4
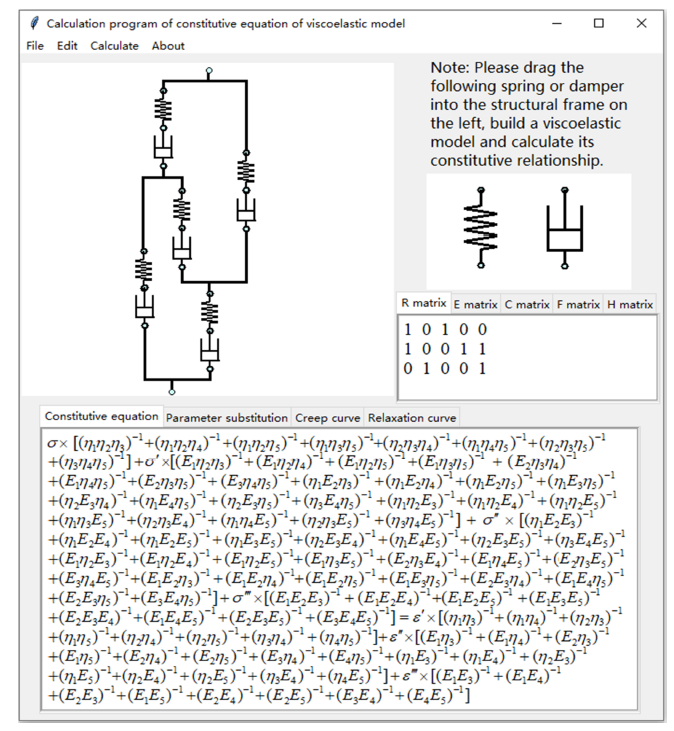
2 Python计算程序示例
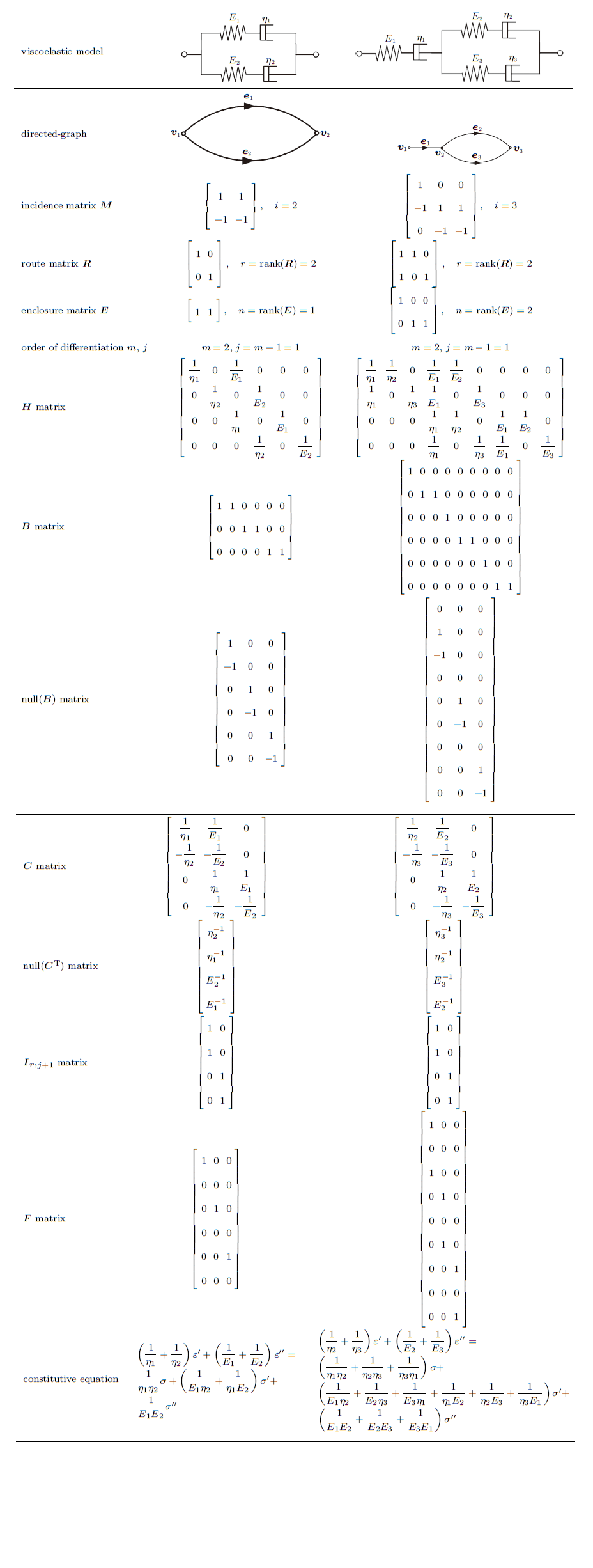
基于以上推导的计算方法,利用Python编写了图形用户界面程序(如图5 所示),可以实现自由搭建模型和计算本构方程等功能。如将软件界面右侧的弹簧或阻尼器拖入左侧图框中,即可构造以任意的连接方式组成的线性黏弹性模型。程序在鼠标拖拽的同时会自动识别各个弹性元件或黏性元件的连接结构,若自动识别的连接结构不符合要求,还可以通过<编辑>菜单进行调整。黏弹性模型构建完毕后即可转换得到与之相对应的有向图,并得到关联矩阵$M$。在<计算>菜单中可设置相关参数并进行计算,如采用符号计算或是数值计算,零空间矩阵的求解方法等等。程序按照图6 所示的流程图可快速计算出黏弹性模型的微分形式的本构方程。并在此基础上,由本构方程计算松弛模量、蠕变柔度、复模量等描述黏弹性材料的基本物理量。计算结果输出在程序界面下方的图框内,也可输出中间计算结果(如独立路径矩阵$R$、闭包围矩阵$E$等等)。通过多个模型的测试,利用该程序均能快速正确地计算出黏弹性模型的本构方程。其中表1 为2个简单黏弹性模型的算例,依据图6 所示的计算流程,给出了中间过程及最终结果。程序还可继续扩展,开发具有其他功能的代码。
图5
图5
程序界面及10元件模型的计算结果
Fig.5
Program interface and results of 10-component model
图6
图6
线性黏弹性模型本构方程计算流程图
Fig.6
Calculation flow chart of constitutive equation of linear viscoelastic model
表1 中右侧所示模型,若令$\eta_{2}$和$E_{3}$为无穷大,表示阻尼$\eta_{2}$处和弹簧$E_{3}$处为刚性连接,即与图1 (d)所示的Burgers模型等价。按照式(34)计算得到的本构方程中,$\eta_{2}$和$E_{3}$都出现在分母的位置,令$\eta_{2}$和$E_{3}$为无穷大,则倒数为零,可以很方便计算得到Burgers模型的本构方程为
(36) $\dfrac{1}{\eta_{3} }{\varepsilon }'+\dfrac{1}{E_{2} }{\varepsilon }"=\dfrac{1}{\eta_{3} \eta_{1} }\sigma +\\\qquad \lt(\dfrac{1}{E_{2} \eta_{3} }+\dfrac{1}{\eta_{1} E_{2} }+\dfrac{1}{\eta_{3} E_{1} }){\sigma }'+\dfrac{1}{E_{1} E_{2} }{\sigma }"\qquad$
3 结语
诸多工程材料如塑料、橡胶、沥青等具有随时间变化的力学响应,如恒载荷下的蠕变、恒定变形下的应力松弛和卸载时的延迟应变恢复等现象。材料的这些黏弹性特征对它们承载时的力学性能有着重要的影响。为了从数学上对黏弹性材料的应力-应变规律进行描述,常利用弹性元件和黏性元件以及它们的组合来建立模型,模拟材料的黏弹性行为。一般来说,弹簧和阻尼器数量越多,模型能够模拟的黏弹性特征也会越来越贴近实际材料。但是,元件越多,模型的本构方程的计算也越复杂。对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,本文推导出了其微分型本构方程的一般矩阵形式的计算方法。首先通过添加弹性参数或黏性参数为无穷大的虚加元件,将存在非Maxwell基本单元的模型扩展为由Maxwell基本单元构成的标准模型。然后将标准模型转化为与之对应的有向图,根据图论的有关知识,基于有向图的特征,由独立路径的形式可以写出基本应变方程,由闭包围的形式可以写出基本应力方程,并根据式(35)对其求适当阶数的导数,按照图6 所示的计算流程可以得到独立路径矩阵、闭包围矩阵及其他中间结果,通过各系数矩阵的运算,即可根据式(34)直接得到模型的微分型本构方程的矩阵形式表述。本文总结了一套适合计算机编程的固定范式,编写了Python程序,可方便搭建黏弹性模型及快速计算其本构关系,并在此基础上可继续开发具有其他功能的代码。
参考文献
View Option
[1]
Wineman A . Nonlinear viscoelastic solids-a review
Mathematics and Mechanics of Solids 2009 , 14 (3 ):300 -366
DOI
URL
[本文引用: 1]
[2]
郑灶锋 , 蔡袁强 , 徐长节 . 稳态荷载下轴对称成层饱和黏弹性地基动力响应
岩石力学与工程学报 , 2005 , 24 (13 ):2380 -2385
[本文引用: 1]
Zheng Zaofeng Cai Yuanqiang Xu Changjie . Axisymmetric dynamic response on layered saturated viscoelsatic soils under steady-state loads
Chinese Journal of Rock Mechanics and Engineering 2005 , 24 (13 ):2380 -2385 (in Chinese)
[本文引用: 1]
[3]
杨林德 , 颜建平 , 王悦照 等 . 围岩变形的时效特征与预测的研究
岩石力学与工程学报 , 2005 , 24 (2 ):212 -216
[本文引用: 1]
Yang Linde Yan Jianping Wang Yuezhao , et al . Study on time-dependent properties and deformation prediction of surrounding rock
Chinese Journal of Rock Mechanics and Engineering 2005 , 24 (2 ):212 -216 (in Chinese)
[本文引用: 1]
[4]
范家参 . 非线性阻尼作用下标准线性固体黏弹性III型破裂的解析解
应用数学和力学 , 2000 , 21 (4 ):415 -423
[本文引用: 1]
Fan Jiashen . Analytical solution for mode III dynamic rupture of standard linear viscoelastic solid with nonlinear damping
Applied Mathematics and Mechanics 2000 , 21 (4 ):415 -423 (in Chinese)
DOI
URL
[本文引用: 1]
[5]
Ren S Zhao G Zhang S . Elastic-viscoelastic composite sructures analysis with an improved burgers model
Journal of Vibration and Acoustics 2018 , 140 (3 ):1 -10
[本文引用: 1]
[6]
Huang C Wang F Gao T , et al . A new viscoelastic mechanics model for the creep behaviour of fibre reinforced asphalt concrete
Frattura ed Integrità Strutturale 2018 , 12 (45 ):108 -120
DOI
URL
[本文引用: 1]
[7]
尹志勇 , 蔡绍皙 , 王正国 . 血液黏弹性五元模型及其生理意义
重庆大学学报(自然科学版) , 1999 (2 ):3 -5
[本文引用: 1]
Yin Zhiyong Cai Shaoxi Wang Zhengguo . The 5-element viscoelasticity model of the blood and the physiological signification
Journal of Chongqing University $($Natural Sciences$)$ 1999 (2 ):3 -5 (in Chinese)
[本文引用: 1]
[8]
候之超 , 赵培 , 高江华 . 泡沬塑料单向压缩本构关系的分数导数模型研究
中国科技论文在线 , 2009 , 4 (10 ):765 -770
[本文引用: 1]
Hou Zhichao Zhao Pei Gao Jianghua . Constitutive model with fractional derivatives for polyurethane foams under uniaxial compression
Sciencepaper Online 2009 , 4 (10 ):765 -770 (in Chinese)
[本文引用: 1]
[9]
李兆生 , 谭忆秋 . 沥青混合料冻融损伤特性研究
中国科技论文 , 2014 , 9 (11 ):1279 -1281
[本文引用: 1]
Li Zhaosheng Tan Yiqiu . Research on asphalt mixture freezing-thawing damage performance
China Sciencepaper 2014 , 9 (11 ):1279 -1281 (in Chinese)
[本文引用: 1]
[10]
詹小丽 , 张肖宁 , 王端宜 等 . 改性沥青非线性黏弹性本构关系研究及应用
工程力学 , 2009 , 26 (4 ):187 -191
[本文引用: 1]
Zhan Xiaoli Zhang Xiaoning Wang Duanyi , et al . Study on nonlinear viscoelastic constitutive equation of modified asphalt and its applications
Engineering Mechanics 2009 , 26 (4 ):187 -191 (in Chinese)
[本文引用: 1]
[11]
潘文潇 , 谭文长 . 广义Maxwell黏弹性流体在两平板间的非定常流动
力学与实践 , 2003 , 25 (1 ):19 -22
[本文引用: 1]
Pan Wenxiao Tan Wenchang . An unsteady flow of a viscoelastic fluid with the fractional Maxwell model between two parallel plates
Mechanics in Engineering 2003 , 25 (1 ):19 -22 (in Chinese)
[本文引用: 1]
[12]
杨挺青 . 黏弹性力学 . 武汉 : 华中科技大学出版社 , 1990
[本文引用: 1]
Yang Tingqing . Theory of Viscoelastility . Wuhan : Huazhong University of Science and Technology Press , 1990 (in Chinese)
[本文引用: 1]
[13]
曾祥国 , 陈华燕 , 陈军 . 黏弹性力学 . 成都 : 四川大学出版社 , 2016
[本文引用: 1]
Zeng Xiangguo Chen Huayan Chen Jun . Theory of Viscoelastility . Chengdu : Sichuan University Press , 2016 (in Chinese)
[本文引用: 1]
[14]
蔡峨 . 黏弹性力学基础 . 北京 : 北京航空航天大学出版社 , 1989
[本文引用: 2]
Cai E . The Fundament of Viscoelastic Mechanics . Beijing : Beijing University of Aeronautics and Astronautics Press , 1989 (in Chinese)
[本文引用: 2]
Nonlinear viscoelastic solids-a review
1
2009
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
稳态荷载下轴对称成层饱和黏弹性地基动力响应
1
2005
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
稳态荷载下轴对称成层饱和黏弹性地基动力响应
1
2005
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
围岩变形的时效特征与预测的研究
1
2005
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
围岩变形的时效特征与预测的研究
1
2005
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
非线性阻尼作用下标准线性固体黏弹性III型破裂的解析解
1
2000
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
非线性阻尼作用下标准线性固体黏弹性III型破裂的解析解
1
2000
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
Elastic-viscoelastic composite sructures analysis with an improved burgers model
1
2018
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
A new viscoelastic mechanics model for the creep behaviour of fibre reinforced asphalt concrete
1
2018
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
血液黏弹性五元模型及其生理意义
1
1999
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
血液黏弹性五元模型及其生理意义
1
1999
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
泡沬塑料单向压缩本构关系的分数导数模型研究
1
2009
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
泡沬塑料单向压缩本构关系的分数导数模型研究
1
2009
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
沥青混合料冻融损伤特性研究
1
2014
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
沥青混合料冻融损伤特性研究
1
2014
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
改性沥青非线性黏弹性本构关系研究及应用
1
2009
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
改性沥青非线性黏弹性本构关系研究及应用
1
2009
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
广义Maxwell黏弹性流体在两平板间的非定常流动
1
2003
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
广义Maxwell黏弹性流体在两平板间的非定常流动
1
2003
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
1
1990
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
1
1990
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
1
2016
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
1
2016
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
2
1989
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
... 一般的黏弹性力学教材中都给出了各种基本模型的微分型本构方程[14 ] ,如:Maxwell模型、Kelvin模型、Poynting-Thomson模型、Burgers模型等等.由于弹性元件和黏性元件数量不多,它们的本构方程推导过程并不难.为了实现计算机编程计算本构方程,以下利用图论算法和矩阵运算,通过推导由10个弹性元件和黏性元件构成的较为复杂模型的应力-应变微分关系,总结和建立任意线性黏弹性模型的微分型本构方程的一般形式. ...
2
1989
... 黏弹性材料广泛应用于各类工程中,如塑料、橡胶等工业材料,土壤、沥青等地质材料,肌肉、血液等生物材料,不胜枚举.由于黏弹性材料兼具弹性与黏性两种特性,其力学性能依赖于环境温度、加载时间、加载速率和幅值等条件,因此建立合适的模型,准确地描述材料的黏弹性行为,对工程应用及理论研究都具有十分重要的意义.材料黏弹性特性的描述和本构方程的表达是黏弹性力学的重要研究内容之一.为了描述黏弹性材料的应力-应变规律,常利用弹性元件和黏性元件以及它们的各种组合构成的模型来进行模拟.如Maxwell模型(图1 (a))、Kelvin模型(图1 (b))、Poynting-Thomson模型(图1 (c))、Burgers模型(1(d))、广义Maxwell模型、广义Kelvin模型等等.多年来,人们开发了各种各样的模型来表征材料的黏弹性特性,对黏弹性材料的本构方程的数学描述进行了大量的研究[1 ] .利用这些模型,诸多学者在各个工程领域开展了大量的研究.例如,将土体视为黏弹性材料,郑灶锋等[2 ] 利用Merchant模型研究了稳态载荷频率和黏滞性对地基振动的影响,研究电站地下厂房洞室围岩的变形规律时,杨林德等[3 ] 基于Kelvin-Voigt模型来模拟和计算围岩的黏弹性变形特征.范家参[4 ] 采用Poynting-Thomson模型对断裂动力学问题进行了研究.Ren等[5 ] 利用改进的Burgers模型,探究了黏弹性复合材料结构的振动特征.Huang等[6 ] 利用改进的Burgers模型来描述沥青混凝土的黏弹性本构行为.为了更准确地表征血液的流变特性,更好地与高切变率下的实验数据相吻合,人们也常常采用由更多元件组成的黏弹性模型来进行相关研究[7 ] .候之超等[8 ] 利用分数微分方程描述泡沫材料的黏弹性特征,研究了单向恒速率加载下模型的力学响应.李兆生等[9 ] 利用广义Maxwell模型构建损伤力学本构模型,研究了沥青材料的冻融损伤过程.詹小丽等[10 ] 采用分数阶导数Maxwell模型对沥青的动态黏弹性力学性能进行了研究.潘文潇等[11 ] 研究了两平板之间的广义Maxwell黏弹性流体非定常流动的解析解.不同的模型具有不同的优缺点,如Maxwell模型可以模拟应力松弛现象,但不能表示蠕变过程;Kelvin模型能够模拟蠕变,却不能表示应力松弛[12 -13 ] .一般来说,随着弹簧和阻尼器数量的增多,模型能够模拟的黏弹性特征也会越来越贴近实际材料[14 ] .但是,对于多个弹簧和阻尼器以任意连接方式组成的黏弹性模型,其微分型本构方程如何快速计算出,是各种基于黏弹性材料结构计算的基础.图论算法可方便快捷地计算路径等问题,而有向图的路径和闭包围又与黏弹性模型的应力方程和应变方程存在联系,以计算由10个弹性元件和黏性元件构成的较为复杂的模型的微分本构方程为例,推导得到了任意线性黏弹性模型的微分型本构方程的一般矩阵形式,总结了一套适合计算机编程的固定范式.并利用Python语言编写了图形界面用户程序,可快速地构建任意复杂的线性黏弹性模型和计算其应力-应变微分关系式.该计算方法对准确地构建实际工程材料的黏弹性计算模型、精确地拟合实际工程材料的黏弹性特性及应力-应变规律具有一定的参考意义. ...
... 一般的黏弹性力学教材中都给出了各种基本模型的微分型本构方程[14 ] ,如:Maxwell模型、Kelvin模型、Poynting-Thomson模型、Burgers模型等等.由于弹性元件和黏性元件数量不多,它们的本构方程推导过程并不难.为了实现计算机编程计算本构方程,以下利用图论算法和矩阵运算,通过推导由10个弹性元件和黏性元件构成的较为复杂模型的应力-应变微分关系,总结和建立任意线性黏弹性模型的微分型本构方程的一般形式. ...