力学与实践, 2022, 44(2): 351-357 DOI: 10.6052/1000-0879-21-378

应用研究

线性强化型弹塑性弯曲直梁挠曲线方程1)

陈英杰,1), 冯永强, 董静波

燕山大学建筑工程与力学学院,河北秦皇岛 066004

河北省土木工程绿色建造与智能运维重点实验室,河北秦皇岛 066004

DEFLECTION CURVE EQUATION OF LINEAR STRENGTHENED ELASTIC-PLASTIC BENDING STRAIGHT BEAM1)

CHEN Yingjie,1), FENG Yongqiang, DONG Jingbo

College of Architectural Engineering and Mechanics, Yanshan University, Qinhuangdao 066004, Hebei, China

Hebei Province Civil Engineering Key Laboratory of Green Construction and Intelligent Operation and Maintenance, Qinhuangdao 066004, Hebei, China

通讯作者: 1)陈英杰,教授,主要从事能量原理在工程中的应用和智能材料等方面的研究。E-mail:cyjysu@126.com

责任编辑: 胡漫 王永会

收稿日期: 2021-09-6   修回日期: 2021-10-29  

Received: 2021-09-6   Revised: 2021-10-29  

作者简介 About authors

摘要

针对材料在弹塑性阶段的应用不完全问题,本文用弹塑性分区最小势能原理,推导出线性强化模型下弯曲直梁的势能分区准则和欧拉方程。求解出集中载荷作用下悬臂梁和简支梁的挠曲线方程,将挠曲线方程代入MATLAB软件进行数值计算并将其结果与ANSYS对比分析。结果表明：数值解与有限元值均满足实际工程中允许的误差范围,给出的方法可为解决工程实际问题提供一个新的思路。

关键词： 弹塑性分区变分最小势能原理; 弹塑性势能分区准则; 欧拉方程; 挠曲线方程

Abstract

Aiming at the incomplete application of materials in elastic-plastic stage. In this paper, by using the principle of elastic-plastic partition minimum potential energy, thecriterion of potential energy and Euler equation of bending straight beam under linear strengthening model are derived. The deflection curve equation of cantilever beam and simply supported beam under concentrated load issolved. The deflection curve equation is put into Matlab software for numerical calculation, and the results are compared with ANSYS. The results show that both the numerical solution and the finite element value meet the allowable error range in practical engineering. The proposed method provides a new idea for solving practical engineering problems.

Keywords： principle of elastic-plastic zone variational minimum potential energy; elastic-plastic potential energy partition criterion; Euler's equation; deflection curve equation

PDF (637KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

陈英杰, 冯永强, 董静波. 线性强化型弹塑性弯曲直梁挠曲线方程1). 力学与实践, 2022, 44(2): 351-357 DOI:10.6052/1000-0879-21-378

CHEN Yingjie, FENG Yongqiang, DONG Jingbo. DEFLECTION CURVE EQUATION OF LINEAR STRENGTHENED ELASTIC-PLASTIC BENDING STRAIGHT BEAM1). Mechanics in Engineering, 2022, 44(2): 351-357 DOI:10.6052/1000-0879-21-378

一直以来,弹塑性[1-2]问题是广大学者所研究的重要课题之一。直梁作为建筑结构中的基本构件,在受到载荷作用下会产生弯曲变形,即弹性变形和塑性变形。为了求解弹性区和塑性区的弯曲变形,需要掌握弹塑性弯曲直梁的基本原理和计算方法。基于材料弹塑性变形的研究如下。钱伟长[3-4]讨论了多种载荷和边界条件梁的问题;张福范[5]早期研究弹性薄板,得出了系列的薄板理论;付宝连[6]提出了划分弹性区和塑性区变分原理。

本文采用弹塑性分区变分最小势能原理[7-9],对集中载荷作用下悬臂梁和简支梁为例的线性强化弹塑性材料进行势能分区准则和欧拉方程的推导,根据推导出的公式求解不同塑性区高度状态下的弹塑性弯曲直梁的挠曲线方程。用MATLAB软件对求解的挠曲线方程进行数值计算和有限元模拟,得出结果分析。

1 线性强化弹塑性悬臂梁的欧拉方程

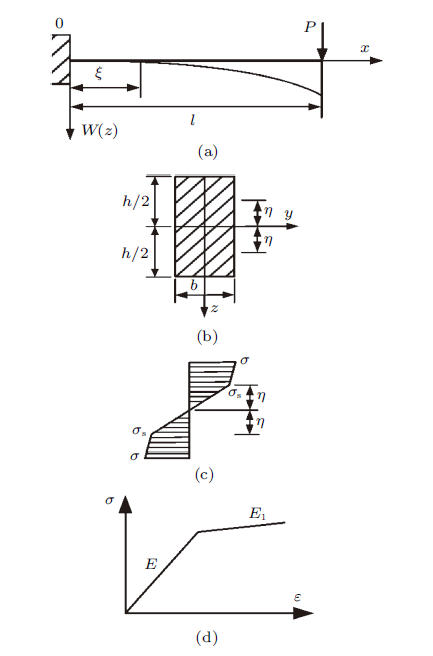
首先选择一个长度为$l$的线性强化弹塑性材料的悬臂梁,在悬臂梁右端施加一个集中载荷$P$,如图1(a)所示。假设在长度$0\sim\xi $范围内,梁体发生弹塑性变形,在长度$\xi \sim l$范围内,梁体发生弹性变形。梁的矩形横截面如图1(b)所示,在长度为$0\sim\xi $段范围内,沿着$z$轴方向,假设在$0\sim \eta $范围内为弹性变形,在$\eta \sim {h/2}$范围内发生塑性变形,假设在横截面的应力分布如图1(c)所示。其中$\xi$为跨内弹塑性长度,$\eta$为梁截面内弹性受力区高度,$h$为横截面高度,$b$为横截面宽度,$\sigma_{{\rm s}} $为屈服应力。图1(d)中,$E$和$E_1$为弹性模量,$\sigma$为应力,$\varepsilon$为应变。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   集中载荷作用下的线性强化悬臂梁

Fig.1   Linearly strengthened cantilever beam under concentrated load


弹性阶段的应力表示为

$\sigma_{{\rm s}} =E\varepsilon$

线性强化阶段应力表示为

$\sigma =E_{1} \varepsilon +\sigma_{{\rm s}} \left( {1-\dfrac{E}{E_{1} }}\right)$

因此,弹塑性阶段任意截面弯矩式可以写为

$M_{1} =2b\int_0^\eta E k_{1} z^{2}{\rm d}z+2b\int_\eta^{h/2}$

$\begin{aligned}M_{1} &=2 b \int_{0}^{\eta} E k_{1} z^{2} \mathrm{~d} z+2 b \int_{\eta}^{h / 2} \sigma z \mathrm{~d} z=\\& \frac{3}{2} M_{\mathrm{e}}\left[1-\frac{1}{3}\left(\frac{k_{\mathrm{e}}}{k_{1}}\right)^{2}\right]+\\& \frac{3}{2} M_{\mathrm{e}} \frac{E_{1}}{E}\left[\frac{2}{3}\left(\frac{k_{1}}{k_{\mathrm{e}}}\right)+\frac{1}{3}\left(\frac{k_{\mathrm{e}}}{k_{1}}\right)^{2}-1\right]\end{aligned}$

式中,$k_1$为弹塑性区的曲率,$k_{\rm e}$为弹塑性区与弹性区交界处的曲率,$M_{{\rm e}}$为弹塑性区与弹性区交界处的弯矩。

弯曲直梁的应变能为

$\begin{aligned}U_{\mathrm{b}}=& \int^{k_{1}}\left\{\frac{3}{2} M_{\mathrm{e}}\left[1-\frac{1}{3}\left(\frac{k_{\mathrm{e}}}{k_{1}}\right)^{2}\right]+\right.\\&\left.\frac{3}{2} M_{\mathrm{e}} \frac{E_{1}}{E}\left[\frac{2}{3}\left(\frac{k_{1}}{k_{\mathrm{e}}}\right)+\frac{1}{3}\left(\frac{k_{\mathrm{e}}}{k_{1}}\right)^{2}-1\right]\right\} \mathrm{d} k_{1}=\\& \frac{3}{2} M_{\mathrm{e}}\left(k_{1}+\frac{1}{3} \frac{k_{\mathrm{e}}^{2}}{k_{1}}\right)+\\& \frac{3}{2} M_{\mathrm{e}} \frac{E_{1}}{E}\left(\frac{1}{3} \frac{k_{1}^{2}}{k_{\mathrm{e}}}-\frac{1}{3} \frac{k_{\mathrm{e}}^{2}}{k_{1}}-k_{1}\right)+C\end{aligned}$

当梁体弹塑性阶段曲率$k_{1} =k_{{\rm e}} $时,$U_{{\rm b}}=M_{{\rm e}} k_{{\rm e}}/2$,可得到

$C=-\dfrac{3}{2}M_{{\rm e}} k_{{\rm e}} \left( {1-\dfrac{E_{1} }{E}} \right)$

弯曲直梁的总势能为

$\begin{aligned}\Pi_{p}=& \int_{0}^{\xi} \mathrm{d} x \int^{k_{1}}\left\{\frac{3}{2} M_{\mathrm{e}}\left[1-\frac{1}{3}\left(\frac{k_{\mathrm{e}}}{k_{1}}\right)^{2}\right]+\right.\\&\left.\frac{3}{2} M_{\mathrm{e}} \frac{E_{1}}{E}\left[\frac{2}{3}\left(\frac{k_{1}}{k_{\mathrm{e}}}\right)+\frac{1}{3}\left(\frac{k_{\mathrm{e}}}{k_{1}}\right)^{2}-1\right]\right\} \mathrm{d} k_{1}+\\& \int_{\xi}^{1} \frac{1}{2} E J\left(\frac{\mathrm{d}^{2} \omega_{2}}{\mathrm{~d} x^{2}}\right) \mathrm{d} x-P \omega_{2(x=l)}\end{aligned}$

式中,$\omega_2$为弹性区挠度,$\varPi$代表混合总势能,下标$p$为一集中载荷。

由变分法基本公式,对式(5)中的$\eta,\xi,\omega $分别变分并取极值得

$\delta \Pi=\delta_{\eta} \Pi_{\mathrm{p}}+\delta_{\xi} \Pi_{\mathrm{p}}+\delta_{\omega} \Pi_{\mathrm{p}}=0$

对$\eta $进行变分计算得

$\eta =\dfrac{\sigma_{{\rm s}} }{Ek_{1} }$

对$\xi $进行变分得

$\begin{array}{c}\delta_{\xi} \Pi_{p}=\left[\frac{3}{2} M_{\mathrm{e}}\left(k_{1}+\frac{1}{3} \frac{k_{\mathrm{e}}^{2}}{k_{1}}\right)+\right. \\\frac{3}{2} M_{\mathrm{e}} \frac{E_{1}}{E}\left(\frac{1}{3} \frac{k_{1}^{2}}{k_{\mathrm{e}}}-\frac{1}{3} \frac{k_{\mathrm{e}}^{2}}{k_{1}}-k_{1}\right)- \\\left.\frac{3}{2} M_{\mathrm{e}} k_{\mathrm{e}}\left(1-\frac{E_{1}}{E}\right)\right]_{x=\xi}^{-}= \\\frac{1}{2} E J\left(\frac{\mathrm{d}^{2} \omega_{2}}{\mathrm{~d} x^{2}}\right)_{x=\xi}^{2}=0\end{array}$

当$x=\xi $时,梁体弹塑性阶段曲率$k_{1} =k_{{\rm e}} $,则有

$\dfrac{1}{2}M_{{\rm e}} k_{{\rm e}} -\dfrac{1}{2}EJ\left({\dfrac{{\rm d}^{2}\omega_{2} }{{\rm d}x^{2}}} \right)^{2}=0$

对$\omega $进行变分计算,并取极值,可以得到欧拉方程为

$\begin{array}{c}\frac{\mathrm{d}^{2}}{\mathrm{~d} x^{2}}\left[\frac{3}{2} M_{\mathrm{e}}\left(1-\frac{E_{1}}{E}\right)-\frac{1}{2} M_{\mathrm{e}}\left(1-\frac{E_{1}}{E}\right)\left(\frac{k_{\mathrm{e}}}{k_{1}}\right)+\right. \\\left.M_{\mathrm{e}} k_{\mathrm{e}} \frac{E_{1}}{E} \frac{k_{1}}{k_{\mathrm{e}}}\right]=0, \quad 0 \leqslant x \leqslant \xi\end{array}$
$\begin{array}{r}{\left[\frac{3}{2} M_{\mathrm{e}}\left(1-\frac{E_{1}}{E}\right)-\frac{1}{2} M_{\mathrm{e}}\left(1-\frac{E_{1}}{E}\right)\left(\frac{k_{\mathrm{e}}}{k_{1}}\right)+\right.} \\\left.M_{\mathrm{e}} k_{\mathrm{e}} \frac{E_{1}}{E} \frac{k_{1}}{k_{\mathrm{e}}}\right]_{x=\xi}+\left(E J \frac{\mathrm{d}^{2} \omega_{2}}{\mathrm{~d} x^{2}}\right)_{x=\xi}=0\end{array}$
$\begin{array}{c}\frac{\mathrm{d}}{\mathrm{d} x}\left[\frac{3}{2} M_{\mathrm{e}}\left(1-\frac{E_{1}}{E}\right)-\frac{1}{2} M_{\mathrm{e}}\left(1-\frac{E_{1}}{E}\right)\left(\frac{k_{\mathrm{e}}}{k_{1}}\right)+\right. \\\left.M_{\mathrm{e}} k_{\mathrm{e}} \frac{E_{1}}{E} \frac{k_{1}}{k_{\mathrm{e}}}\right]_{x=\xi}+\left(E J \frac{\mathrm{d}^{3} \omega_{2}}{\mathrm{~d} x^{3}}\right)_{x=\xi}=0\end{array}$
$E J \frac{\mathrm{d}^{4} \omega_{2}}{\mathrm{~d} x^{4}}=0, \quad \xi \leqslant x \leqslant l$
$\left(E J \frac{\mathrm{d}^{2} \omega_{2}}{\mathrm{~d} x^{2}} \delta \frac{\mathrm{d} \omega_{2}}{\mathrm{~d} x}\right)_{x=\xi}=0$
$E J\left(\frac{\mathrm{d}^{3} \omega^{2}}{\mathrm{~d} x^{3}}\right)_{x=l}+P=0$

式(9)~式(14)是欧拉方程;式(7)是弹塑性区$Z$轴方向弹性区和塑性区的分区准则。式(8)是$X$轴方向弹塑性区和弹性区的分区准则。

根据式(3)可以求得集中载荷作用下的线性强化梁的近似解为

$k_{1}=k_{\mathrm{e}} \sqrt{\frac{2}{3-\frac{2 M_{1}}{M_{\mathrm{e}}} \frac{E}{E-E_{1}}+\frac{2 E_{1}}{E-E_{1}} \frac{2 M_{\mathrm{e}}-M_{1}}{M_{\mathrm{e}}}}}$

2 集中载荷作用下线性强化弹塑性悬臂梁的计算

2.1 挠曲线方程推导

首先取一个理想弹塑性材料悬臂梁,应用弹塑性弯曲直梁的弹塑性分区最小势能原理对这一悬臂梁进行计算,并求解其在相应的载荷作用下的相关变形问题。一个受到集中载荷作用下的线性强化弹塑性悬臂梁,如图1所示。

假设端部弯矩为

$ M_{1} \left( x \right)=C_{1} x+C_{2} $

由$x=0$处的端部弯矩,得

$ M_{1} \left( x \right)=P\left( {l-x} \right) $

在$x=\xi $处的弯矩为

$ M_{{\rm e}} =\dfrac{bh^{2}}{6}\sigma_{{\rm s}} =P\left( {l-\xi }\right) $

将式(15)代入式(7),并注意到式(17)和式(18),整理运算得

$ \eta \left( x \right)=\dfrac{h}{2}\sqrt {3-\dfrac{2\left( {E+E_{1} }\right)\left( {l-x} \right)}{\left( {E-E_{1} } \right)\left( {l-\xi }\right)}+\dfrac{4E_{1} }{E-E_{1} }} $

将式(17)和式(18)代入式(15)进行积分运算,整理得弹塑性区挠度

$ \begin{aligned}\omega_{1}=& \frac{2 \sigma_{\mathrm{s}}}{E h}\left\{( E - E _ { 1 } ) ( l - \xi ) \left[\left(3 E+E_{1}\right)(l-\xi)-\right.\right.\\&\left.\left.2\left(E+E_{1}\right)(l-x)\right]^{3}\right\}^{1 / 2} /\left[3\left(E+E_{1}\right)^{2}\right]+\\& C_{3} x+C_{4}\end{aligned} $

在x=0端,$\omega_{1x} =[d \omega_{1}/(dx)]_{x=0} =0$,可以求出$C_{3}$和$C_{4} $,并代入式(20),整理得

$ \begin{aligned}\omega_{1}=& \frac{2 \sigma_{\mathrm{s}}}{E h}\left\{( E - E _ { 1 } ) ( l - \xi ) \left[\left(3 E+E_{1}\right)(l-\xi)-\right.\right.\\&\left.\left.2\left(E+E_{1}\right)(l-x)\right]^{3}\right\}^{1 / 2} /\left[3\left(E+E_{1}\right)^{2}\right]-\\& \frac{2 \sigma_{\mathrm{s}}}{E h} x\left\{( E - E _ { 1 } ) ( l - \xi ) \left[\left(3 E+E_{1}\right)(l-\xi)-\right.\right.\\&\left.\left.2 l\left(E+E_{1}\right)\right]\right\}^{1 / 2} /\left(E+E_{1}\right)-\\& \frac{2 \sigma_{\mathrm{s}}}{E h}\left\{( E - E _ { 1 } ) ( l - \xi ) \left[\left(3 E+E_{1}\right)(l-\xi)-\right.\right.\\&\left.\left.2 l\left(E+E_{1}\right)\right]^{3}\right\}^{1 / 2} /\left[3\left(E+E_{1}\right)^{2}\right]\end{aligned} $

在弹性阶段$\xi \leqslant x\leqslant l$时的曲率与弯矩的关系为

$ \dfrac{{\rm d}^{2}\omega_{2} }{{\rm d}x^{2}}=\dfrac{P}{EJ}\left( {l-x}\right) $

$P=bh^{2}\sigma_{s}/[6(l-\xi)]$,对式(22)进行积分得

$ \omega_{2} =\dfrac{\sigma_{{\rm s}} }{Eh\left( {l-\xi } \right)}\left({lx^{2}-\dfrac{1}{3}x^{3}} \right)+C_{5} x+C_{6} $

在$x=\xi$处,有$\omega_{1(x=\xi)} =\omega_{2(x=\xi)}$和$[dw_{1}/(dx)]_{x=\xi}=dw_{2}/(dx)]_{x=\xi}$,求出$C_{5}$和$C_{6}$

当$x=l$时,将求出的$C_{5}$和$C_{6} $代入式(23),整理得

$ \begin{aligned}\omega_{2}=& \frac{2 \sigma_{\mathrm{s}} l^{3}}{3 E h(l-\xi)}+\frac{2 \sigma_{\mathrm{s}} l}{E h} \frac{\left(E-E_{1}\right)(l-\xi)}{E+E_{1}}-\frac{2 \sigma_{\mathrm{s}} l^{2}}{E h(l-\xi)} \xi+\frac{\sigma_{\mathrm{s}} l}{E h(l-\xi)} \xi^{2}-\\& \frac{2 \sigma_{\mathrm{s}} l}{E h} \frac{\sqrt{\left(E-E_{1}\right)(l-\xi)\left[\left(3 E+E_{1}\right)(l-\xi)-2 l\left(E+E_{1}\right)\right]}}{E+E_{1}}+\frac{2 \sigma_{\mathrm{s}}}{E h} \frac{\left(E-E_{1}\right)^{2}(l-\xi)^{2}}{3\left(E+E_{1}\right)^{2}}-\\& \frac{2 \sigma_{\mathrm{s}}}{E h} \frac{\left(E-E_{1}\right)(l-\xi)}{E+E_{1}} \xi-\frac{2 \sigma_{\mathrm{s}}}{E h} \frac{\sqrt{\left(E-E_{1}\right)(l-\xi)\left[\left(3 E+E_{1}\right)(l-\xi)-2 l\left(E+E_{1}\right)\right]^{3}}}{3\left(E+E_{1}\right)^{2}}+\\& \frac{\sigma_{\mathrm{s}} l}{E h(l-\xi)} \xi^{2}-\frac{2 \sigma_{\mathrm{s}}}{3 E h(l-\xi)} \xi^{3}\end{aligned} $

当全梁皆为弹性时,有

$\omega_{2(x=0)} =[d\omega_{2}/(dx)]_{x=0}=0$

于是,当x=l时,

$ \omega_{2(x=l)} =\dfrac{2\sigma_{{\rm s}} l^{3}}{3Eh\left( {l-\xi }\right)} $

2.2 数值计算

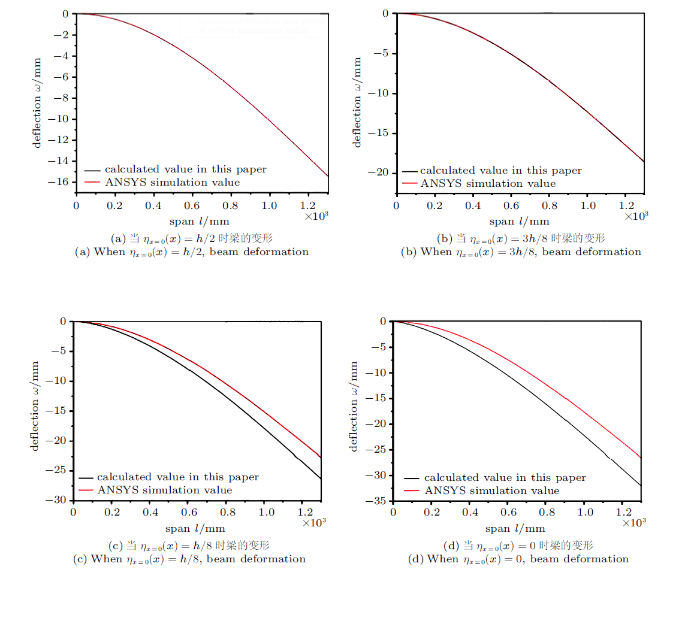
应用MATLAB软件对$\eta_{x=0} \left(x\right)$为${h}/{2}$, ${3h}/{8}$, ${h}/{8}$,0时线性强化型弹塑性悬臂梁的弯曲方程进行编程,求解其挠度值;弹塑性梁的基本参数：梁长$l=1300$ mm,梁宽$b=80$ mm,梁高$h=120$ mm,杨氏模量$E=210 000$ MPa,强化后杨氏模量$E_1=0.1E$,泊松比$v=0.3$,屈服应力$\sigma_{{\rm s}}=345$ MPa。应用有限元模拟软件,依据弹塑性悬臂梁实际边界条件和基本参数进行建模,求解弹塑性悬臂梁的挠度值,由于本文所求的是细长弹塑性弯曲直梁,且不考虑剪切变形,故采用beam23单元双线性等向强化模型进行ANSYS模拟。计算出沿梁全长的模拟与理论挠度结果如图2(a)~图2(d)所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   梁截面内弹性受力区不同高度处挠度分布图

Fig.2   Deflection distribution at different heights of elastic zone in beam section


2.3 结果分析

根据图2(a)~图2(d)可以得到固定端截面,当弹性区高度$\eta_{x=0}(x)$在$0\sim {h/8}$范围时,随着弹性区高度的增加误差越来越小。而弹性区高度$\eta_{x=0} \left( x \right)$在${{3h}/8}\sim {h/2}$范围内误差较小,且本文方法与有限元模拟求解的挠度基本吻合。从图2可以看出,本文方法与ANSYS模拟求解弹塑性悬臂梁自由端的误差均在允许范围内,表明本文的方法能准确地计算线性强化型弹塑性材料的弹性区与塑性区的边界问题。

3 集中载荷作用下线性强化弹塑性简支梁的计算

3.1 挠曲线方程推导

将弹塑性弯曲直梁弹塑性分区最小势能原理应用于一个线性强化弹塑性材料简支梁,计算其变形问题。

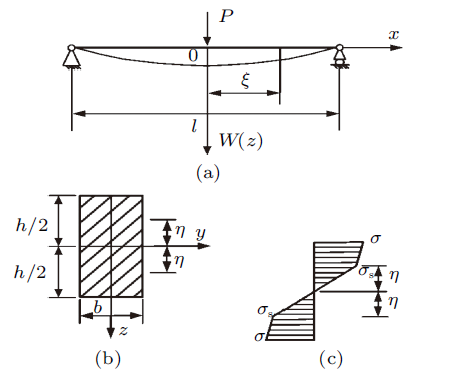
图3所示为一个跨中受集中载荷作用下的弹塑性简支梁。其中$\eta$为梁跨中截面内弹性受力区高度,$\xi $为梁跨内弹塑性区长度。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   跨中受集中载荷作用下的弹塑性简支梁

Fig.3   Elastic-plastic simple-supported beam under concentrated load in mid-span


对简支梁弯矩做如下假设

$M_{1} \left( x \right)=C_{1} x+C_{2}$

据$x=0$处的端部弯矩和$x=\xi $处的弯矩,得

$ M_{1} \left( x \right)=-\dfrac{P}{4}\left( {l-2x} \right) $

在$x=\xi $处的弯矩为

$ M_{{\rm e}} =\dfrac{bh^{2}}{6}\sigma_{{\rm s}} =\dfrac{P}{4}\left( {l-2\xi }\right) $

将式(27)和式(28)代入式(19),整理得

$ \eta \left( x \right)=\dfrac{h}{2}\sqrt{3-\dfrac{2\left( {E+E_{1} }\right)\left( {l-2x} \right)}{\left( {E-E_{1} } \right)\left( {l-2\xi }\right)}+\dfrac{4E_{1} }{E-E_{1}}} $

将式(27)和式(28)代入式(15)进行积分运算,整理得

$ \omega_{1}=\frac{2 \sigma_{\mathrm{s}}}{E h} \sqrt{\frac{\left(E-E_{1}\right)(l-2 \xi)\left[\left(3 E+E_{1}\right)(l-2 \xi)-2\left(E+E_{1}\right)(l-2 x)\right]^{3}}{12\left(E+E_{1}\right)^{2}}}+C_{3} x+C_{4} $

在$x=0$端,$\left[\mathrm{d} \omega_{1} /(\mathrm{d} x)\right]_{x=0}=0$,可以求出$C_{3} $,并代入式(30),整理得

$ \begin{array}{c}\omega_{1}=\frac{2 \sigma_{\mathrm{s}}}{E h} \sqrt{\frac{\left(E-E_{1}\right)(l-2 \xi)\left[\left(3 E+E_{1}\right)(l-2 \xi)-2\left(E+E_{1}\right)(l-2 x)\right]^{3}}{12\left(E+E_{1}\right)^{2}}}- \\\frac{2 \sigma_{\mathrm{s}}}{E h} x \sqrt{\frac{\left(E-E_{1}\right)(l-2 \xi)\left[\left(3 E+E_{1}\right)(l-2 \xi)-2 l\left(E+E_{1}\right)\right]}{2\left(E+E_{1}\right)}}+C_{4}\end{array} $

在弹性阶段$\xi \leqslant x\leqslant l$时,曲率与弯矩的关系为

$ \dfrac{{\rm d}^{2}\omega_{2} }{{\rm d}x^{2}}=\dfrac{P}{4EJ}\left( {l-2x}\right) $

$P=2 b h^{2} \sigma_{\mathrm{s}} /[3(l-2 \xi)]$,对式(32)进行积分计算,且$x={l}/{2}$处,有$\omega_{2(x={l}/{2})} =0$,得

$C_{6} =-\dfrac{\sigma_{{\rm s}} l^{3}}{6Eh\left( {l-2\xi }\right)}-\dfrac{1}{2}C_{5}$
$\omega_{2} =\dfrac{\sigma_{{\rm s}} }{Eh\left( {l-2\xi } \right)}\left({lx^{2}-\dfrac{2}{3}x^{3}} \right)+\\\qquad C_{5} \left( {x-\dfrac{l}{2}}\right)-\dfrac{\sigma_{{\rm s}} l^{3}}{6Eh\left( {l-2\xi } \right)} $

由$x=\xi $,有$\omega_{1(x=\xi)} =\omega_{2(x=\xi)} $和$\left[{{{\rm d}\omega_{1} }/({{\rm d}x}}) \right]_{x=\xi } =\left[{{{\rm d}\omega_{2} }/({{\rm d}x}}) \right]_{x=\xi }$,求出$C_{4},C_{5},C_{6} $,并代入式(31)和式(34),整理得

$ \begin{aligned}\omega_{1}=& \frac{2 \sigma_{\mathrm{s}}}{E h} \sqrt{\frac{\left(E-E_{1}\right)(l-2 \xi)\left[\left(3 E+E_{1}\right)(l-2 \xi)-2\left(E+E_{1}\right)(l-2 x)\right]^{3}}{12\left(E+E_{1}\right)^{2}}}+\\& \frac{\sigma_{\mathrm{s}}}{E h}(l-2 x) \sqrt{\frac{\left(E-E_{1}\right)(l-2 \xi)\left[\left(3 E+E_{1}\right)(l-2 \xi)-2 l\left(E+E_{1}\right)\right]}{2\left(E+E_{1}\right)}} \\& \frac{2 \sigma_{\mathrm{s}}}{E h} \frac{\left(E-E_{1}\right)^{2}(l-2 \xi)^{2}}{12\left(E+E_{1}\right)^{2}}-\frac{\sigma_{\mathrm{s}}}{E h} \frac{\left(E-E_{1}\right)(l-2 \xi)^{2}}{2\left(E+E_{1}\right)}-\frac{\sigma_{\mathrm{s}} l^{3}}{6 E h(l-2 \xi)}+\\& \frac{\sigma_{\mathrm{s}} l^{2}}{E h(l-2 \xi)} \xi-\frac{3 \sigma_{\mathrm{s}} l}{2 E h(l-2 \xi)} \xi^{2}+\frac{\sigma_{\mathrm{s}}}{3 E h(l-2 \xi)} \xi^{3}\end{aligned} $
$ \begin{array}{l}\omega_{2}=\frac{\sigma_{\mathrm{s}}}{E h(l-2 \xi)}\left(l x^{2}-\frac{2}{3} x^{3}\right)-\frac{\sigma_{\mathrm{s}} l^{3}}{6 E h(l-2 \xi)}+\\x\left[\frac{2 \sigma_{\mathrm{s}}}{E h} \frac{\left(E-E_{1}\right)(l-2 \xi)}{2\left(E+E_{1}\right)}-\frac{2 \sigma_{\mathrm{s}} l}{E h(l-2 \xi)} \xi+\frac{\sigma_{\mathrm{s}}}{E h(l-2 \xi)} \xi^{2}\right]+\\\frac{\sigma_{\mathrm{s}}}{E h}(l-2 x) \sqrt{\frac{\left(E-E_{1}\right)(l-2 \xi)\left[\left(3 E+E_{1}\right)(l-2 \xi)-2 l\left(E+E_{1}\right)\right]}{2\left(E+E_{1}\right)}}-\\\frac{\sigma_{\mathrm{s}} l}{E h} \frac{\left(E-E_{1}\right)(l-2 \xi)}{2\left(E+E_{1}\right)}+\frac{\sigma_{\mathrm{s}} l^{2}}{E h(l-2 \xi)} \xi-\frac{\sigma_{\mathrm{s}} l}{2 E h(l-2 \xi)} \xi^{2}\end{array} $

当全梁皆为弹性时,在x=0处有$[dw_{2}/(dx)]_{x=0}$,$x={l}/{2}$处有$\omega_{2(x={l}/{2})}=0$,得

$ C_{5} =0,\ \ C_{6} =-\dfrac{\sigma_{{\rm s}} l^{3}}{6Eh\left( {l-2\xi }\right)} $

所以当$x=0$时

$ \omega_{2} =-\dfrac{\sigma_{{\rm s}} l^{3}}{6Eh\left( {l-2\xi }\right)} $

3.2 数值计算

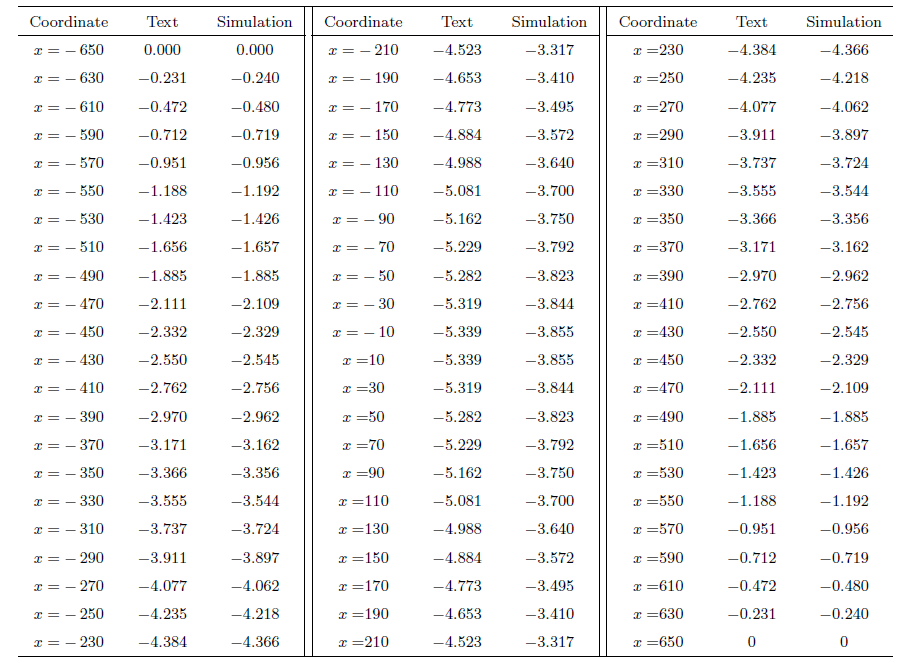
应用MATLAB软件对$\eta_{x=0} \left( x\right)={h}/{4}$时弹塑性简支梁的弯曲方程进行编程,计算出沿梁全长,每间隔20 mm处竖直方向的理论和模拟挠度值,列于表1。依据弹塑性简支梁实际边界条件和弹塑性梁 基本参数进行建模,求解挠度值。由于本文所求的是细长弹塑性弯曲直梁,且不考虑剪切变形,故采用beam23单元进行ANSYS模拟。

表1   当$\eta_{x=0} \left( x \right)={h}/{4}$时理论与模拟挠度数值

Table 1  When $\eta_{x=0} \left( x \right)={h}/{4}$,theoretical and simulated deflection values

新窗口打开| 下载CSV


3.3 结果分析

根据表1,可以得到在跨中截面,当弹性区高度在$\eta_{x=0} \left(x\right)={h/4}$时,弯曲直梁沿着$x$轴方向变化的挠度计算值和模拟值,通过对比分析,可以得到本文方法计算得出的挠度与有限元模拟求解的挠度基本吻合。从表1可以看出,本文方法与ANSYS模拟求解弹塑性简支梁跨中的误差均在允许范围内,这表明本文方法对于求解弹塑性下梁的变形计算具有很好的适用性,能准确地计算线性强化性材料的弹性区和塑性区的边界问题。

4 结论

本文依据弹塑性分区最小势能原理,对集中载荷作用下悬臂梁和简支梁的挠曲变形进行了求解,经过数值计算结果与模拟值进行对比分析,表明线性强化模型下对集中载荷作用于悬臂梁和简支梁求解的挠曲线方程正确。说明本文方法能准确计算出线性强化型弹塑性材料的弹性区和塑性区的分界问题,并为接下来弹塑性材料的进一步研究与应用提供了一个新的思路。

参考文献

刘协权, 倪新华, 刘云庭.

线性强化材料空间杆系弹塑性分析

西安科技学院学报, 2002, 22(4):489-492

[本文引用: 1]

Liu Xiequan, Ni Xinhua, Liu Yunting.

Elastoplastic analysis of spatial bars of linear strengthening materials

Journal of Xi'an University of Science and Technology, 2002, 22(4):489-492 (in Chinese)

[本文引用: 1]

张系斌.

带屈服平台线性强化材料的弹塑性梁的变形分析

长江大学学报(自然科学版), 2005, 2(10): 273-274, 364-368

[本文引用: 1]

Zhang Xibin..

Deformation analysis of elastic plastic beam with linear strengthening material with yield platform

Journal of Changjiang University $($Natural Science Edition$)$, 2005, 2(10): 273-274, 364-368 (in Chinese)

[本文引用: 1]

钱伟长. 变分法及有限元(上册). 北京: 科学出版社, 1980

[本文引用: 1]

Qian Weichang. Variational Method and Finite Element (Volume I). Beijing: Science Press, 1980 (in Chinese)

[本文引用: 1]

钱伟长.

高阶拉氏乘子法和弹性理论中更一般的广义变分原理

应用数学和力学, 1983, 4(2):137-150

[本文引用: 1]

Qian Weichang.

Higher order Lagrange multiplier method and more general variational principle in elastic theory

Applied Mathematics and Mechanics, 1983, 4(2):137-150 (in Chinese)

[本文引用: 1]

张福范. 弹性薄板. 北京: 科学出版社, 1984

[本文引用: 1]

Zhang Fufan. Elastic Thin Plate. Beijing: Science Press, 1984 (in Chinese)

[本文引用: 1]

付宝连. 弹性力学中的能量原理及其应用. 北京: 科学出版社, 2004

[本文引用: 1]

Fu Baolian. Energy Principle and Its Application in Elasticity. Beijing: Science Press, 2004 (in Chinese)

[本文引用: 1]

丁光涛.

变分法逆问题研究的若干进展

北京大学学报(自然科学版), 2016, 52(4):732-740

[本文引用: 1]

Ding Guangtao.

Some advances in the study of inverse problems of variational method

Journal of Peking University $($Natural Science Edition$)$, 2016, 52(4):732-740 (in Chinese)

[本文引用: 1]

胡海昌.

论弹性体力学与受范性体力学中的一般变分原理

物理学报, 1954, 10(3):259-290

Hu Haichang.

On general variational principles in elastic mechanics and normed body mechanics

Journal of physics, 1954, 10(3):259-290 (in Chinese)

Tonti E.

Variational principles in elastostatics

Meccanica, 1967, 2(4):201-208

DOI      URL     [本文引用: 1]

/

〈 〉