高强度管线钢的工程应用一直是管道行业热点和追求的目标。1959年,高强度低合金钢在美国Great Lake管线系统中获得首次应用,随着管线钢的组织结构不断得到优化,管线钢的强度和延性不断提高^[1]。由于管道是一种典型的焊接结构,焊缝及靠近焊缝的母材及热影响区不可避免地存在各种形式的焊接缺陷,如裂纹、气孔、夹渣、未焊透、未熔合等^[2]。我国近年来已发生多起高钢级管道事故,多表现为管道环焊缝的应变能力不足。环焊缝的应变能力与其力学性能密切相关,因而研究管道环焊缝断裂韧性测试至关重要。J积分阻力曲线(J-R曲线)作为管道等钢结构完整性评定的重要参数,通常从试件的断裂韧性测试中获得,如单边缺口弯曲(single edge notch bending, SENB)试件和紧凑拉伸(compact tension, CT)试件。而对于管道环焊缝等浅裂纹条件,通常采用裂纹尖端具有较低约束的单边缺口拉伸(single edge notch tension, SENT)试件进行。

材料的断裂韧性在弹性范围内通常采用裂纹应力强度因子表征,而在弹塑性范围内通常采用J积分或者裂纹尖端张开位移(crack tip opening displacement, CTOD)进行表征。自20世纪60年代以来,国内外对断裂韧性测试方法进行了较为广泛的研究,各种断裂韧性试验方法在世界范围内得到了充分发展^[3]。其中,最常用的标准试件是SENB试件和CT试件,而这些标准试样在裂纹尖端具有较高的约束条件。实践表明,对于管道环焊缝等浅裂纹条件,由于裂纹尖端约束较小,使用标准CT试件或SENB试件测量的断裂韧性通常过于保守。因此,适用于管道环焊缝等低约束条件下的断裂韧性测试方法应运而生^[4]。在石油和天然气行业中,通常采用SENT试件测量管道低约束状态下的J积分或CTOD,用以表征材料在低约束状态的断裂韧性。该方法已成功应用于海底和陆地管道基于应变的设计、工程临界分析以及适用性评价,大大节省了管道设计和维护成本,促进了管道断裂韧性测试的研究^[5-7]。

挪威船级社(DNV)、加拿大矿物与能源研究中心(CANMET)、埃克森美孚公司(ExxonMobil)分别于2006年、2008年、2010年针对J-R曲线和CTOD阻力曲线测试提出了三种具有代表性的SENT试件测试方法,其中DNV方法为多试样法,另外两者为单试样法^[8-12]。英国标准协会(BSI)在2014年12月发布了第一个SENT试件测试标准BS 8571^[13]。然而,BS 8571主要是基于标准DNV-RP-F108^[8]提出的,因而具有一定的局限性;美国材料与试验协会(ASTM)出版的SENB和CT试样阻力曲线测试标准ASTM E1820^[14]并不适用于SENT试件;我国也尚未出版关于低约束SENT试件断裂韧性的测试标准。采用低约束试件测试管道环焊缝的断裂韧性有较多需要解决的技术难题^[15],然而目前未有文献针对厚宽比$B/W=2$的SENT试件以及侧槽深度为10%的SENT试件进行研究。

因此,本文针对试件厚宽比$B/W=2$的SENT试件,首先,采用三维有限元分析方法建立SENT试件有限元模型;其次,分析考虑裂纹长宽比、材料硬化指数、试件侧槽对J积分塑性因子的影响;最后,根据模拟结果,拟合SENT试件J积分塑性因子方程,此方程用于SENT的断裂韧性测试,可提高测试准确性。

根据标准BS 8571^[13],J积分弹性分量($J_{{\rm el}}$)可由应力强度因子(K)确定,即

式中,$E$和$\nu$分别表示弹性模量和泊松比。

对于加载水平和几何结构确定的SENT试件,采用有限元方法计算试件J积分,J积分塑性部分($J_{\rm pl}$)可按式(2)进行计算。

载荷-位移曲线下塑性区面积可按式(3)进行计算

式中,$A$为载荷-位移曲线下的总面积,$A_{{\rm el}}$为载荷-位移曲线下弹性区面积,$P$为载荷,$C_{0}$为加载柔度。

根据文献[16],J积分塑性因子$\eta_{{\rm pl}}$可按式(4),利用标准化塑性J积分和标准化塑性区面积进行计算

式中,$\bar{{J}}_{{\rm pl}} $和$\bar{{A}}_{{\rm pl}}$分别表示标准化塑性J积分和标准化塑性区面积,$\sigma_{0}$为材料的屈服强度,$B$为试件厚度,$b$为试件韧带长度。

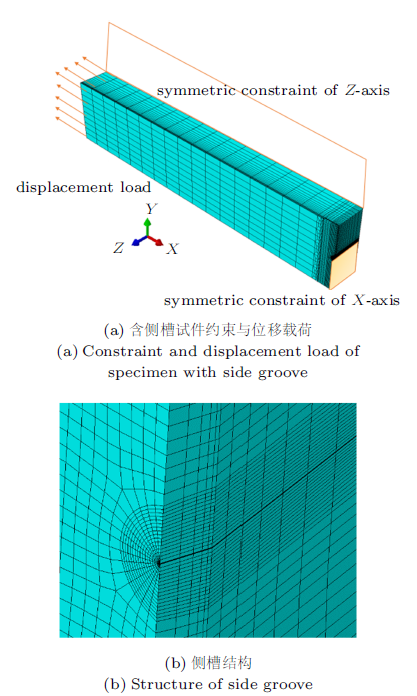
采用ABAQUS软件进行有限元分析,建立三维侧槽深度为10%$B$与不含侧槽SENT试件有限元模型。由于试件为对称结构,采用C3D8R单元建立四分之一有限元模型。模拟中试件宽度固定不变,取$W=20$ mm;裂纹长宽比($a/W$)分6种情况,即$a/W$分别为0.2,0.3,0.4,0.5,0.6,0.7;根据标准BS 8571^[13],试件厚宽比$B/W=2$;试件夹持端距离($H$)固定不变,取$H=10W$。分析中假设裂纹不发生扩展。对于含侧槽试件,根据标准BS 8571^[13],推荐侧槽深度占试件厚度的10%。为了细化裂纹尖端网格,裂纹尖端采用2.5 $\mu$ m钝化圆弧过渡,以提高低变形水平下J积分的计算,该裂纹尖端网格可以较为准确地确定裂纹尖端的应力、应变场,有利于J积分的精确计算。

模型沿厚度方向共分为15层,厚度方向从中间对称面到试件自由表面逐层递减,以捕捉试件表面裂纹前沿的高应力、应变场梯度。裂纹长宽比$a/W=0.5$,试件厚宽比$B/W=2$时,侧槽深度10%$B$的SENT试件的有限元模型如图1所示。

采用Ramberg-Osgood模型描述材料真应力($\sigma $)和真应变($\varepsilon$)关系,即

式中,屈服强度$\sigma_{\rm Y}=510$ MPa,弹性模量$E=200$ GPa,$\alpha$为硬化系数。模拟5种不同硬化指数材料,分别取硬化指数($n$)为5, 7, 10, 15, 20,对应材料的极限强度分别为1273 MPa, 933 MPa, 752 MPa,643 MPa,597 MPa,材料的屈强比分别为0.4,0.54,0.68,0.79,0.85。

模拟过程中采用位移载荷进行控制,在试件端面施加位移载荷,每次分为2000个加载步,采用完全Newton-Raphson迭代法求解非线性方程组,每步迭代次数最大为50次。因此每个SENT试件可以获得2000组载荷线位移、裂纹嘴张开位移以及J积分数据,选取处于线性段数据进行J积分塑性因子计算。在给定的加载步骤中,采用虚拟裂纹扩展法计算J积分,对于$a/W=0.5$,$B/W=2$,$n=10$的含侧槽SENT试件,所提取的19圈J积分结果的最大偏差不超过3.8%。厚度方向上,除自由表面外,将各层J积分取平均值用于计算J积分塑性因子。

J积分塑性因子根据计算方式可以分为基于载荷线位移的J积分塑性因子($\eta_{\rm LLD}$)和基于裂纹嘴张开位移的J积分塑性因子($\eta_{\rm CMOD}$)。对于$a/W=0.5$,$n=10$的不含侧槽SENT试件,其标准化J积分($\bar{J}_{\rm pl}$)和基于载荷线位移与基于裂纹嘴张开位移的标准化塑性区面积($\bar{A}_{\rm pl}$)的关系如图2所示。可知,当$a/W$一定时,$\eta_{\rm LLD}$在初始阶段随载荷增加逐渐下降,随着载荷的提升,曲线斜率逐渐趋于常数。$\eta_{\rm CMOD}$在整个加载范围内均基本保证恒定,表明基于裂纹嘴张开位移的J积分塑性因子与加载水平无关。

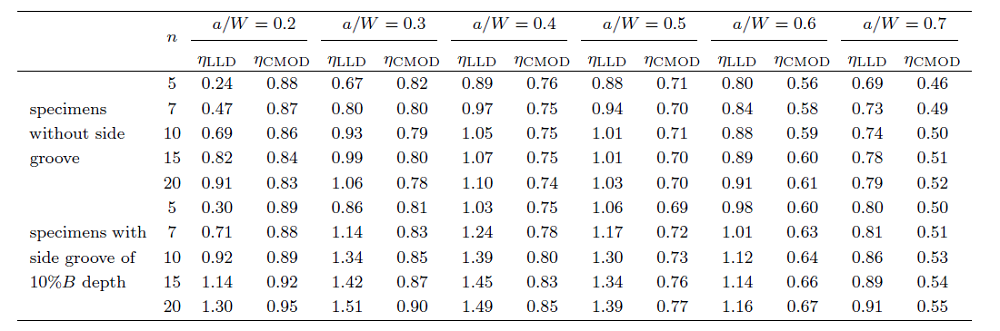
选取J积分处于线性阶段数据计算J积分塑性因子,结果见表1。可知,当试件的$a/W$和$n$相同时,侧槽深度10%$B$的J积分塑性因子远大于不含侧槽试件。因为在相同的加载水平下,含侧槽试件裂纹前沿的局部J积分分布更均匀,平均J积分高于相同载荷水平下不含侧槽试件,导致含侧槽试件的J积分塑性因子更高。

J积分塑性因子计算结果与文献^[8,9]中结果对比见图3。可知,$\eta_{\rm LLD}$和$\eta_{\rm CMOD}$与$a/W$密切相关。$\eta_{\rm LLD}$初始随着$a/W$的增加而提升,直到$a/W$达到0.3~0.4,之后随着$a/W$的增加而逐渐下降。$\eta_{\rm CMOD}$随着$a/W$的增加而减小。该规律与文献^[16]和文献^[8]等方法结果基本一致。

不同硬化指数下,侧槽深度10%$B$的SENT试件J积分塑性因子计算结果见图4。可知,$\eta_{\rm LLD}$通常随$n$的增加而增大。而不含侧槽SENT试件,$\eta_{\rm CMOD}$在$a/W<0.5$时,随$n$的增加而减小,而在$a/W\geqslant0.5$时,随$n$的增加而增大;侧槽深度10%$B$的SENT试件,$\eta_{\rm CMOD}$除$a/W=0.2$外,均随$n$的增加而增大。$n$对$\eta_{\rm LLD}$影响相对较大,而对$\eta_{\rm CMOD}$影响较小。相较不含侧槽的SENT试件,侧槽深度10%$B$的SENT试件J积分塑性因子对于硬化指数更为敏感。

为了便于使用SENT试件对J积分进行实验评估,当试件$B/W=2$,基于表1中所计算的$\eta_{\rm LLD}$和$\eta_{\rm CMOD}$,采用式(6)和式(7)拟合关于裂纹长宽比的多项式方程计算J积分塑性因子

式中,$p_{i}$和$q_{i}$为多项式系数。为了考虑硬化指数对J积分塑性因子的影响,采用材料屈强比代表材料的硬化性能,对多项式系数$p_{i}$和$q_{i}$进行了拟合。关于屈强比的多项式系数$p_{i}$和$q_{i}$方程分别为

式中,$\sigma_{{\rm b}}$为材料的拉伸强度, 拟合系数$M_{ij}$和$N_{ij}$分别见表2。所提出的多项式方程考虑了裂纹长宽比和硬化指数的影响。

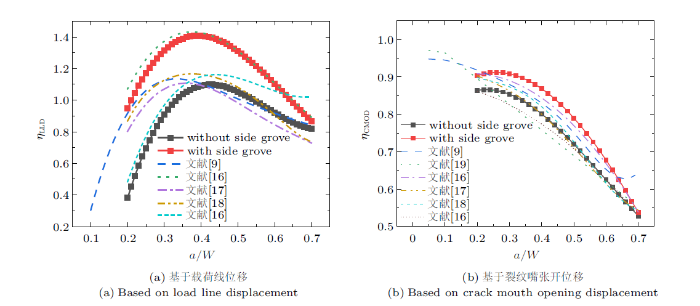
当$n=10$时,基于载荷线位移和基于裂纹嘴张开位移的J积分塑性因子拟合公式(6)和式(7)与文献^[15,16]中J积分塑性因子公式对比见图5。可知,对于不含侧槽SENT试件,由式(6)计算的$\eta_{\rm LLD]$在$a/W\geqslant 0.4$时与文献^[16]中结果较为接近,而当在$a/W<0.4$时,本文提出的公式值相对偏小。这是因为不同方法中,模拟过程所考虑的材料的硬化指数、试件几何尺寸、有限元分析方法(2D和3D有限元模型)等存在一定差异。由式(6)计算的含侧槽SENT试件$\eta_{\rm LLD}$普遍高于文献中结果,而略小于文献^[16]提出的侧槽深度15%$B$的SENT试件J积分塑性因子。对于不含侧槽SENT试件,由式(7)计算的$\eta_{\rm CMOD]$与文献^[16]中结果基本一致;而侧槽深度10%$B$的$\eta_{\rm CMOD}$略高于文献计算结果,这是因为文献结果仅针对试件$B/W=0.5$或$B/W=1$的情况进行,未考虑试件$B/W=2$的情况。

针对管道低约束断裂韧性测试中厚宽比$B/W=2$的SENT试件,采用三维有限元分析方法,建立考虑侧槽的SENT试件三维有限元模型,模拟计算不同裂纹长宽比($a/W=0.2$~0.7、增量0.1)、硬化指数($n=5$,7,10,15,20)下侧槽深度10%与不含侧槽SENT试件J积分塑性因子,主要结论如下。

(1) 基于载荷线位移的J积分塑性因子初始随着裂纹长宽比的增加而提升,直到裂纹长宽比达到0.3~0.4,之后随着裂纹长宽比的增加而逐渐下降。基于裂纹嘴张开位移的J积分塑性因子随着裂纹长宽比的增加而减小。

(2) 当试件的裂纹长宽比、材料硬化指数相同时,含侧槽SENT试件J积分塑性因子远大于不含侧槽试件。

(3) 根据不同情况J积分塑性因子计算结果,提出考虑裂纹长宽比、材料硬化性能、侧槽影响的J积分塑性因子方程,填补SENT试件厚宽比$B/W=2$的J积分塑性因子研究空白,可用于试件厚宽比$B/W=2$的SENT试件断裂韧性测试。