力学与实践, 2022, 44(2): 328-336 DOI: 10.6052/1000-0879-21-303

应用研究

不同截面形状罐体液罐车液体质心特性1)

何烈云,*,2), 李国军†, 周妍*

*浙江警察学院交通管理工程系,杭州 310053

†浙江警察学院公共基础部,杭州 310053

THE CHARACTERISTICS OF THE CENTER OF MASS OF THE LIQUID IN THE TANKER WITH DIFFERENT CROSS SECTION SHAPES1)

HE Lieyun,*,2), LI Guojun†, ZHOU Yan*

*Department of Transportation Management and Engineering, Zhejiang Police Collage, Hangzhou 310053, China

†Department of Public Foundation, Zhejiang Police College, Hangzhou 310053, China

通讯作者: 2)何烈云,副教授,主要研究方向为道路交通安全,道路交通事故再现,交通流理论。E-mail:helieyun@zjjcxy.cn

责任编辑: 胡漫 王永会

收稿日期: 2021-07-21   修回日期: 2021-09-6  

基金资助: 1)浙江省软科学资助项目(2020C35G2321127)

Received: 2021-07-21   Revised: 2021-09-6  

作者简介 About authors

摘要

为获取液罐车作转向行驶时罐内液体质心变化特性,以常见的圆形、椭圆形、多段弧形和方形四种截面形状罐体为研究对象,将液罐车转向行驶时罐内液体视为准静态变化过程,利用均质平面质心计算原理,构建了不同工况条件下的液体质心计算模型,采用MATLAB数值仿真方法,得到了质心坐标及质心轨迹图像,对比分析了不同截面形状罐体的图像规律及车辆侧向稳定特性,研究结论可为液罐车设计及行驶稳定性研究提供依据。

关键词： 液罐车; 质心; 准静态; 截面; 充装率; 侧向加速度

Abstract

In order to investigate the motion of the center of mass of liquid in a turning tank truck, tanks with four common section shapes, i.e., circular, oval, multi-section arc and square, are considered in this research. The liquid in the tank is assumed to be quasi-static during the turning. The liquid center of mass is calculated through the integration of the center of mass for each homogeneous section plane. Using MATLAB, the centroid coordinates and centroid trajectory images are obtained. The lateral stability characteristics of tank trucks with different shape of cross-section is analyzed. The research results provide guidelines for the design and driving stability of liquid tank truck.

Keywords： tank truck; the center of mass; quasi static; cross section; filling rate; lateral acceleration

PDF (1367KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

何烈云, 李国军, 周妍. 不同截面形状罐体液罐车液体质心特性1). 力学与实践, 2022, 44(2): 328-336 DOI:10.6052/1000-0879-21-303

HE Lieyun, LI Guojun, ZHOU Yan. THE CHARACTERISTICS OF THE CENTER OF MASS OF THE LIQUID IN THE TANKER WITH DIFFERENT CROSS SECTION SHAPES1). Mechanics in Engineering, 2022, 44(2): 328-336 DOI:10.6052/1000-0879-21-303

液罐车主要从事危险化学品公路运输,具有质心位置高和运载质量大等特点。为防止工作温度升高而液体膨胀,在充装时罐内必须留有一定气相空间,因此液罐车在变速运动时,液体存在倾斜晃动现象,导致横向稳定性相对于普通货运车辆更差、倾翻交通事故发生率更高、引起事故后果更严重。以沈海高速温岭段"6$\cdot$13"液化石油气运输槽罐车重大爆炸事故为例,此起事故共造成20人死亡,175人入院治疗,其中24人重伤,爆炸中心1000 m范围内的房屋均有不同程度受损,此次事故造成了巨大的经济损失。因此开展液罐车侧倾稳定性研究具有重要的现实意义[1-2]。

国内外学者提出了流体力学模型、准静态力学模型、等效机械模型、数值计算法等研究方法来开展液罐车稳定性研究。流体力学模型可以推导出液罐车转向运动时,罐内液体液面倾斜度及液体对罐体表面的压强,进一步求出液体对罐体的压力和压力矩大小[3]。准静态模型可以较好地预测液面在缓慢变化时液体的质心位置,计算冲击力及对应的侧倾力矩大小,推导侧翻阈值,但对瞬态力学特性较难预测[4-5]。等效机械模型在研究液体晃动规律、罐内液体晃动与车辆运动之间耦合作用较好[6-7]。基于上述研究方法,王琼瑶等[8-9]提出了通过在罐体内优化防波板的形状及覆盖弹性膜的方法,限制液罐车在非满载时罐体内液体的晃动。覆盖弹性膜的方法虽然理论上能够抑制液体的晃动,但是弹性膜的固定位置随充装率的改变而调整,实践中操作不方便。陈铭年等[10]以椭圆矩形截面罐体油罐车为研究对象,将满载时油面线相对于罐体曲线的位置分为四种情况,推导出液体质心的计算模型,并通过对比分析椭圆矩形和椭圆形两种不同截面罐体液罐车的横向稳定性。文献[11,12,13]将罐内晃动液体分为晃动的部分和相对静止的部分,将罐内液体晃动液体质心等效为单摆模型,提出了差动制动防侧翻控制策略。李伟建[14]以圆形横截面罐体液罐车为研究对象,将罐内液体视为理想状态,利用均质平面质心求解方法,通过数学建模方式获得了液面在不同倾斜角的质心轨迹,采用"等效机械摆模型"对液体晃动特性开展模拟仿真。于迪等[15]将罐内液体晃动液体质心等效为"弹簧-质子模型",建立了非满载液罐车罐内液体冲击等效机械模型。陈益苞等[16]提出通过优化罐体形状、调整罐体尺寸参数,减少液体晃动对罐体冲击力,提高液罐车行驶时的侧倾稳定性。

掌握罐内液体质心变化规律是开展液罐车稳定性研究的理论基础,现有成果虽然涉及到液体质心变化规律,提出了液体质心实时位置的计算方法,但现有算法模型往往只针对单一形状罐体且精度有待提高,提出的等效机械模型尚未经过严谨理论和实验证明。本文在国内外现有研究成果的基础上,将液罐车在转向运动时罐内充装的是无旋、不可压缩理想液体,且忽略液体自由表面少量的小碎波影响,以较为复杂的八段圆弧截面罐体质心计算为例,从方便数值积分计算角度,通过细化液罐车在转向运动时工况条件,提高液罐车液体质心计算模型精度,并运用MALAB仿真技术,得到液体质心动态变化特性,分析四种常见罐体横截面的精确液体质心力学特性,在此基础上系统对比研究不同截面形状罐的液罐车横向稳定性。

1 准静态条件下液体质心计算模型

液罐车根据运输液体自身特性及罐体材料的不同,可采用的罐体截面形状也不同,罐体的横截面常见的有正圆形、椭圆形、多段圆弧组合形、矩圆形四种,如图1所示。圆形截面罐体主要用于装运非常压液化气,其余三种形状截面罐体装运常压液体。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   四种常见横截面形状罐体

Fig.1   Four common cross-sectional shapes of tanks


1.1 液罐车转向运动时液面倾斜率

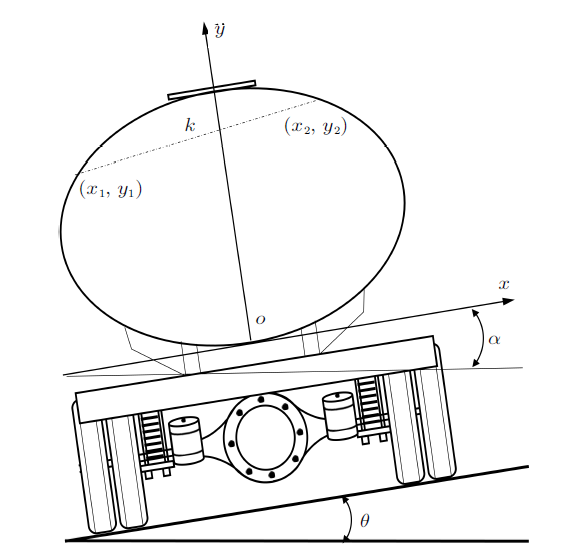
液罐车在转向运动时,若沿行驶方向未采取加减速操作,罐内液体质量沿罐体纵向轴线方向是均匀分布的,且罐体与车辆底盘连接设计时,罐体纵向平面与车辆底盘纵向平面重合,相互之间载荷为均布载荷,因此分析液罐车侧倾稳定力学特性时,可以取罐体横截面受力即可[3]。

假设罐内充装的是无旋、不可压缩且密度均匀液体,以椭圆横截面罐体为例,设椭圆形罐体的长半轴为$a$,短半轴为$b$,建立如图2所示坐标,$x$轴与长轴平行,$y$轴与短轴重合,原点设在椭圆形下象限点处,令液面与罐体两个交点坐标分别为($x_{1}, y_{1}$)和($x_{2}, y_{2}$)。液罐车在转向运动时,罐体的侧倾角为$\alpha$,道路超高设计坡度角为$\theta $,即道路超高值$i=\tan\theta $。$\alpha$大小与液罐车悬架左右侧弹簧钢板变形量差值有关。设车辆转向运动时侧向加速度为$a_{\rm n}$,重力加速度为$g$,由文献[3]可知液面的斜率为

$ k=\frac{{g}\sin {(\theta -\alpha )}-{a}_{\rm n}\cos {(\theta -\alpha )}}{{g}\cos {(\theta -\alpha)}-{a}_{\rm n}\sin {(\theta -\alpha )}} $

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   椭圆形液罐车转向运动液面倾斜分析

Fig.2   Incline analysis of steering motion liquid level of elliptical tank truck


《公路工程技术标准》(JTG B01—2014)规定,道路圆曲线超高值较小,在特殊环境时极限值也不超过10%,即$\theta <0.1$ rad,一般情况下车辆悬架变形引起罐体最大侧倾角度$\alpha \approx 0.06$ rad[17],且$\alpha $与$\theta$接近相互抵消的关系,因此当车辆行驶速率为$v$,转向半径为$r$,液罐车转向行驶时液面斜率表达式可简化为

$k=\frac{v^{2}}{gr}$

参照《公路路线设计规范》(JTG D20—2017),公路设计速度与圆曲线最小半径之间呈对应关系,由公式(2)可知,液罐车罐体内液面斜率值在0.10~0.16范围内变化。

1.2 液体质心计算模型

《公路路线设计规范》(JTG D20—2017)规定,直线与圆曲线连接处、以及半径不同的同向圆曲线相连接处,一般设有回旋曲线和超高渐变段,液罐车按匀速率驶入或驶离圆曲线路段过程时,受到的离心加速度均匀变化。因此车辆在圆曲线路段行驶过程,只要加速度不发生突变且路面是平面的,计算液体质心位置变化就接近准静态模型,自由液面是一条斜线。液体满足准静态变化可以通过简单的试验加以验证,将装有液体的透明罐体放到车辆上,当车辆在曲线路段行驶时,可以清楚观察到罐体内液体的倾斜过程。若液罐车装载为密度均匀的液体,均质平面质心坐标计算公式为

$ \left. {\begin{array}{l} x_{\rm c}=\displaystyle\int \dfrac{x{\rm d}A}{A} \\ y_{\rm c}=\displaystyle\int \dfrac{y{\rm d}A}{A} \\ \end{array}} \right\} $

式中,$A$为液体的横截面面积。

常见多段弧截面结构罐体有8段圆弧组长,圆弧是关于纵向中轴对称,但每段圆弧对应的圆心不在同一点,因此多段弧截面形状罐体液体质心计算最为复杂。在计算质心时为了便于积分,根据液体充装率及液罐车侧向加速度,可分为如图3所示的15种工况。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   八段圆弧截面罐体质心计算工况

Fig.3   Calculation working conditions of centroid of eight-section arc section tank


以工况2为例,建立如图4坐标系,设液面与罐体交点分别为$m$和$n$两点,将液体分成$A_{\rm I}$~$A_{\rm VI}$共6块;图中采用阿拉伯数字下标的坐标为圆弧圆心坐标、采用罗马数字下标的坐标为相邻圆弧的交点坐标;$r_{1}$~$r_{5}$分别为5段圆弧对应的半径。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   八段弧结构罐体截面模型

Fig.4   Section model of tank with eight segment arc structure


根据式(3)和式(4),可先计算$A_{\rm I}$~$A_{\rm VI}$区域每一块面积及质心位置。以$A_{\rm II}$和$A_{\rm V}$两块区域为例,计算方法如下。

(1) $A_{\rm II}$区域面积及质心坐标计算

$A_{\mathrm{II}}=2 \int_{y_{\mathrm{I}}}^{y_{\mathrm{II}}}\left[x_{2}+\sqrt{r_{2}^{2}-\left(x-y_{2}\right)^{2}}\right] \mathrm{d} y$
$ x_{\rm IIC}=0 $
$y_{\mathrm{IIC}}=\frac{2}{A_{\mathrm{II}}} \int_{y_{\mathrm{I}}}^{y_{\mathrm{II}}} y\left[x_{2}+\sqrt{r_{2}^{2}-\left(x-y_{2}\right)^{2}}\right] \mathrm{d} y$

式(4)~式(6)中,$A_{\rm II}$为面积,$x_{\rm IIC}$和$y_{\rm IIC}$为$A_{\rm II}$块质心坐标,$r_{2}$为$A_{\rm II}$块对应圆弧半径,$x_{2}$和$y_{2}$为$A_{\rm II}$区域对应圆弧圆心坐标。

(2)$A_{\rm V}$区域面积及质心坐标计算

$\begin{aligned}A_{\mathrm{V}}=& \frac{x_{m}\left(y_{m}-y_{\mathrm{IV}}\right)}{2}+x_{\mathrm{IV}}\left(y_{\mathrm{IV}}-y_{m}\right)+\\& \int_{x_{\mathrm{IV}}}^{x_{\mathrm{III}}}\left[y_{4}+\sqrt{r_{4}^{2}-\left(x-x_{4}\right)^{2}}-y_{m}\right] \mathrm{d} x\end{aligned}$
$\begin{array}{l}\int_{0}^{x_{\mathrm{IV}}} x\left(y_{\mathrm{IV}}-y_{m}\right) \mathrm{d} x+ \\\left.\int_{x_{\mathrm{IV}}}^{x_{\mathrm{III}}} x\left[y_{4}+\sqrt{r_{4}^{2}-\left(x-x_{4}\right)^{2}}-y_{m}\right] \mathrm{d} x\right\}\end{array}$
$\begin{aligned}y_{\mathrm{VC}} &=\frac{1}{A_{\mathrm{V}}}\left\{\int _ { y _ { m } } ^ { y _ { \mathrm { IV } } } y \left[x_{4}+\sqrt{r_{4}^{2}-\left(y-y_{4}\right)^{2}}-\right.\right.\\&\left.\left.\left(\frac{y-y_{m}}{k}+x_{m}\right)\right] \mathrm{d} y\right\}\end{aligned}$

式(7)~式(9)中,$A_{\rm V}$为面积,$x_{\rm VC}$和$y_{\rm VC}$为$A_{\rm V}$块质心坐标,$r_{4}$为$A_{\rm V}$块对应圆弧半径,$x_{4}$和$y_{4}$为$A_{\rm V}$区域对应圆弧圆心坐标,$k$为液面斜率。

同理求解出其他区域的面积及质心坐标,整个液体截面质心坐标为

$ \left.\begin{array}{rl}x_{\mathrm{AC}} & =\frac{\sum_{i=\mathrm{I}}^{\mathrm{V}} x_{i \mathrm{C} \times} A_{i}}{\sum_{i=\mathrm{I}}^{\mathrm{V}} A_{i}}=\frac{\sum_{i=\mathrm{I}}^{\mathrm{V}} x_{i \mathrm{C} \times} A_{i}}{e \times S} \\y_{\mathrm{AC}}= & \frac{\sum_{i=\mathrm{I}}^{\mathrm{V}} y_{i \mathrm{C} \times} A_{i}}{\sum_{i=\mathrm{I}}^{\mathrm{V}} A_{i}}=\frac{\sum_{i=\mathrm{I}}^{\mathrm{V}} x_{i \mathrm{C} \times} A_{i}}{e \times S}\end{array}\right\} $

式中,$x_{\rm AC}$和$y_{\rm AC}$为液体质心坐标,$S$为罐体横截面积,$e$为液体充装率,即液体$A_{\rm V}$与$S$比值。

根据液罐车充装率、车辆行驶速度、道路半径,并联立质心方程及圆弧方程,可求出液罐车罐内液体质心坐标。其余三种截面罐体液体质心计算原理也相同,不再赘述。

计算不同截面形状罐体液罐车各种工况时液体质心坐标,本文研究时采用了MATLAB进行编程计算,并采用AutoCAD绘图软件作图求解面域质心方法对计算结果进行验证,确保了计算方法及程序语言的准确率。在研究四种截面形状罐体的液罐车液体质心

变化特性时,选取的车型及罐体几何参数如下。

(1) 圆形：以国内某厂家生产的CLW9401GYQC型液化气体运输半挂车为例,该车的圆形截面罐体内直径为2525 mm,筒体长度为10 692.0 mm。

(2) 椭圆形：以国内某厂家生产的HRT5250GYY型运油车为例,该车的椭圆形截面罐体内长半轴为1190 mm,短轴为755 mm,筒体长度为6320 mm。

(3) 多段弧形：以国内某厂家生产的5070GJYH型加油车为例,该车的八段圆弧组合形截面罐体外形尺寸如下。宽度为1800 mm,高度为1250 mm,圆弧半径$r_1=500$ mm,$r_3=1950$ mm,$r_4=500$ mm,$r_5=2950$ mm。

(4) 方形截面罐体并不常见,少部分洒水车罐体采用。方形截面罐体液罐车罐体长度为10 000 mm,宽度为2400 mm,高度为1600 mm。

2 四种罐体截面液罐车质心坐标与充装率关系

为了防止罐内液体因外界温度升高膨胀,造成罐内压力过大导致罐体破损,罐内充装液体留有一定的间隙。以液化气为例,根据《液化气体汽车罐车》(GB/19905—2017)规定,当罐内蒸气压力达到安全阀的整定压力时,充装非易燃易爆液化气液体体积不大于罐体体积的98%,充装易燃易爆液化气对应液体体积不大于罐体体积的95%。罐体充装率是决定液体质心位置的因素之一,对液罐车侧向稳定性有重要影响。

2.1 充装率与罐内液体质心关系

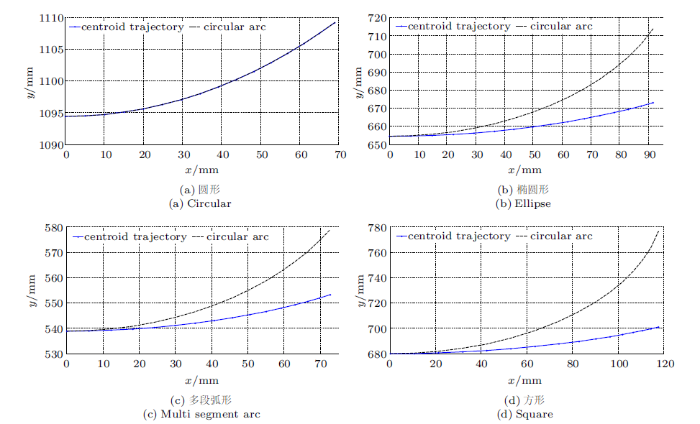
假设液罐车转向行驶时液面倾斜角为15$^\circ$,即侧向加速度约为0.267 9$g$时,充装率初始值为95%,并以$-$5%的步长变化,直到充装率为30%。四种不同罐体截面结构液罐车罐内液体质心坐标图如图5所示。图中动态质心坐标为液罐车在以0.267 9$g$侧向加速度时、不同充装率下液体质心的坐标位置连线;静态质心轨迹为液罐车在平衡状态时、不同充装率下液体质心的坐标位置连线。在图中动态质心坐标点与静态质心坐标点,从上向下充装率是依次对应的关系。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   充装率-液体质心坐标图

Fig.5   Filling rate-liquid centroid coordinate diagram}


2.2 充装率对液体质心位置影响分析

分析图5(a)~图5(d)的液体质心坐标位置连线,呈现以下特性。

(1) 随着充装率逐渐减小,液罐车转向行驶时,液体质心偏移幅度逐渐增大;

(2) 在同一充装率时,液罐车转向运动时质心纵坐标及横坐标同时增大,但横坐标增大量明显大于纵坐标,说明液体的横向晃动量大于纵向晃动量;

(3) 对图5(a)~图5(d)液体质心坐标连线图像采用一次线性函数"$y=ax+b$"进行拟合时,结果如表1所示。

表1   液体质心坐标连线

Table 1  Mass coordinate of liquid center line

新窗口打开| 下载CSV


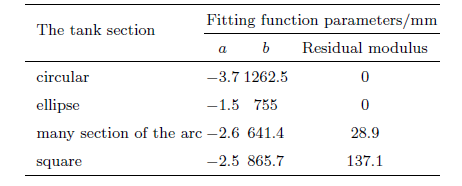
由残差模可知,圆形和椭圆形截面质心坐标连线是标准的一次函数图像,且图像纵向截距位于罐体几何中心处,说明这两种截面罐体液罐车侧向稳定性与充装率之间是线向关系,不存在充装率敏感区间;多段弧形和方形截面质心轨迹图像一次函数拟合程度较差,说明这两种截面罐体液罐车侧向稳定性在不同充装率区间敏感度不一样,尤其在充装率处于55%~85%区间,液罐车侧向稳定性波动大。因此,为提高液罐车的横向稳定性,减少液体的晃动幅度,装载时在符合充装规范的前提下,尽量提高罐体的充装率。

3 四种罐体截面液罐车质心轨迹与侧向加速度

随着侧向加速度增大,罐内液体液面倾斜角度也增大,对应的液体质心位置也发生相应变化,液罐车横向稳定性也变差。

3.1 侧向加速度–罐内液体质心轨迹图

设定液罐车罐体充装率为85%,液罐车侧向加速度初始值为0,并以0.03$g$的步长增加,直到达到0.45$g$。由式(2)可知,对应的液面倾斜角初始值为0$^\circ$,并以3$^\circ$的步长增加,直到液面倾斜角为45$^\circ$。四种不同罐体截面结构液罐车罐内液体质心轨迹如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   侧向加速度-质心轨迹图

Fig.6   Lateral acceleration-center of mass trajectory diagram}


3.2 侧向加速度对液体质心位置影响分析

分析图6(a)~图6(d)的液体质心轨迹图像,呈现出以下特点。

(1) 随着侧向加速度增大,液体质心偏移平衡位置距离越大,且质心沿横向偏移的距离明显比纵向偏移大,说明液罐车的侧翻阈值主要是受质心横向偏移影响;

(2) 液体质心轨迹图像均为光滑凹曲线,说明伴随着侧向加速度增大,液体质心变化是连续的,即使方形罐体也不存在突变点;

(3) 图中圆弧线形是以罐体几何中心为圆心,以平衡状态时液体质心与罐体几何中心间距为半径绘制得到。图6(a)中,质心轨迹与圆弧完美重合,圆形截面罐体质心这一特性同样可以通过AutoCAD作图法验证,同时也进一步验证了本文提出的质心计算模型及采用MATLAB编程计算方法是可行的。图6(c)~图6(d)中,质心轨迹与圆弧完全不重合,且侧向加速度越大,质心坐标偏离圆弧越远。

3.3 侧向加速度对液体质心位置影响分析

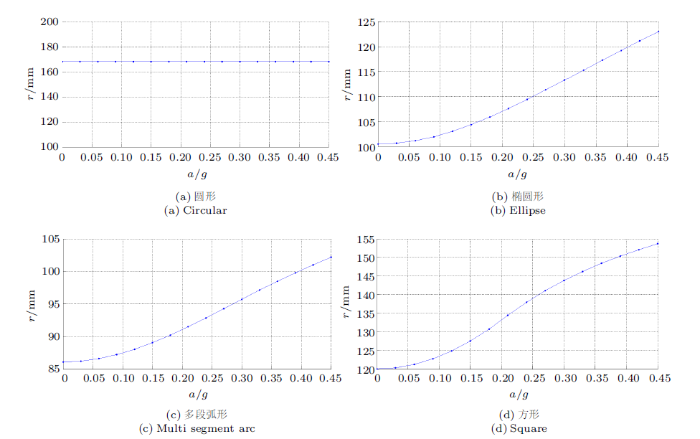
为进一步研究液体质心与罐体几何中心的间距$r$的变化特性,以侧向加速度$a$为横坐标、$r$为纵坐标,得到如图7所示的"$r$-$a$"图像。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   液体质心和罐体几何中心间距-侧向加速度图

Fig.7   Distance between liquid center of mass and tank geometric center-lateral acceleration diagram


(1) 圆形截面罐体内液体质心与罐体几何中心间距为常量,其余三种截面形状罐体内液体质心与罐体几何中心间距则随着侧向加速度增大而增大。

(2) 当侧向加速度$a$小于0.15$g$后,椭圆形和多段弧形两种截面,$r$与$a$是非线性关系,且$r$增加相对缓慢;当侧向加速度$a$大于0.15$g$后,$r$与$a$接近线性关系;而方形截面罐体$r$与$a$始终为非线性关系,且$a$在0.15$g$~0.35$g$间时,$r$的变化较为明显。

以上两个特性说明,文献[11,12,13]中提出液体晃动的等效机械单摆模型只适用于圆形截面结构罐体,而其余三种截面结构罐体内液体晃动等效于摆长随侧向加速度改变的"参数振动"摆模型。图6和图7表明,圆形截面罐体内的液体横向晃动相对较为缓和,车辆的横向稳定性也较好。

4 结论

将液体视为无旋、均质且不可压缩,利用均质平面质心计算公式,提供了圆形、椭圆形、多段弧形、方形四种罐形液罐车,侧向加速度作用下液体质心的建模方法。运用MATLAB数值仿真技术,绘制了在不同工况下四种罐形液罐车的液体质心图像。通过对比分析体质心图像,得出以下研究结论。

(1) 四种罐形液罐车在侧向加速度作用下,罐内液体质心发生偏移,且横向偏移量均明显大于纵向偏移量。

(2) 当侧向加速度相同时,随着充装率减小,四种罐形液罐车的液体质心偏移量均增大。圆形和椭圆形截面罐体内液体质心坐标连线满足一次线性函数,其余两种罐形液罐车的液体质心坐标连线线性拟合程度较差。

(3) 当充装率相同时,随着侧向加速度增大,四种罐形的液体质心偏移量均增大,液体质心轨迹为一段光滑曲线,且圆形截面罐体液罐车的液体质心轨迹是一段圆弧。

以上研究结论为对比不同罐形液罐车的侧向稳定性、合理控制液罐车充装率、构建液体晃动等效机械模型等提供了理论依据。

参考文献

Acarman T, Ozguner U.

Rollover prevention for heavy trucks using frequency shaped sliding mode control

Vehi-cle System Dynamics, 2003, 1(10):7-12

[本文引用: 1]

Romero JA, Ramírez O, Fortanell JM, et al.

Analysis of lateral sloshing forces within road containers with high fill levels

Journal of Automobile Engineering, 2006, 220(3):303-312

DOI      URL     [本文引用: 1]

何烈云, 刘强.

非满载液罐车侧倾稳定性的准静态等效力学模型

力学与实践, 2020, 42(3):294-299

[本文引用: 3]

He Lieyun, Liu Qiang.

A quasi-static equivalent mechanical model for roll stability in partially-filled tanker trucks

Mechanics in Engineering, 2020, 42(3):294-299 (in Chinese)

[本文引用: 3]

Kang X, Rakheja S, Stiharu I.

Cargo load shift and its influence on tank vehicle dynamics under braking and turning

International Journal of Heavy Vehicle Systems, 2002, 9(3):173-203

DOI      URL     [本文引用: 1]

Modaressi-Tehrani K, Rakheja S, Sedaghati R.

Analysis of the overturning moment caused by transient liquidslosh inside a partly filled moving tank

Journal of Automobile Engineering, 2006, 220(3):289-301

DOI      URL     [本文引用: 1]

Li XS, Zheng XL, Ren YY, et al.

Study on driving stability of tank trucks based on equivalent trammel pendulum for liquid sloshing

Discrete Dynamics in Nature and Society, 2013, 2013: 659873(in Chinese)

[本文引用: 1]

郑雪莲, 李显生, 任园园 等.

非满载汽车罐车液体冲击等效机械模型

吉林大学学报(工学版), 2013, 43(6):1488-1493

[本文引用: 1]

Zheng Xuelian, Li Xiansheng, Ren Yuanyuan, et al.

Equivalent mechanical model for liquid sloshing in partially-filled tank vehicle

Journal of Jilin University: Engineering and Technology Edition, 2013, 43(6):1488-1493 (in Chinese)

[本文引用: 1]

王琼瑶, 蒋开洪, Subhash Rakheja, 等.

部分充液罐车内液体晃动的瞬态响应分析

振动与冲击, 2018, 37(17):1-8

[本文引用: 1]

Wang Qiongyao, Jiang Kaihong, Subhash Rakheja, et al.

Transient response analysis of liquid slosh in a liquid-partially filled tank truck

Journal of Vibration and Shock, 2018, 37(17):1-8 (in Chinese)

[本文引用: 1]

王琼瑶, Subhash Rakheja, 上官文斌.

带弹性膜的部分充液罐车罐体内液体横向晃动的瞬态响应分析

振动与冲击, 2019, 38(5):98-105

[本文引用: 1]

Wang Qiongyao, Subhash Rakheja, Shangguan Wenbin.

Liquid slosh in a partially filled liquid tank truck with an elastic membrane

Journal of Vibration and Shock, 2019, 38(5):98-105 (in Chinese)

[本文引用: 1]

陈铭年, 林永智, 徐建全.

椭圆矩形油罐车转弯横向稳定性的计算分析

专用汽车, 2003(5):3-6

[本文引用: 1]

Chen Mingnian, Lin Yongzhi, Xu Jianquan.

Calculate analysis of transversal stabilization for turning of oil tank truck with irregular elliptical section

Special Purpose Vehicle, 2003(5):3-6 (in Chinese)

[本文引用: 1]

杨秀建, 邢云祥, 吴相稷 等.

液罐车液体侧向晃动多质量椭圆规摆模型

交通运输工程学报, 2018, 18(5):140-151

[本文引用: 2]

Yang Xiujian, Xing Yunxiang, Wu Xiangji, et al.

Multimass trammel pendulum model of fluid lateral sloshing for tank vehicle

Journal of Traffic and Transportation Engineering, 2018, 18(5):140-151 (in Chinese)

[本文引用: 2]

赵伟强, 凌锦鹏, 宗长富.

半挂式液罐车防侧翻控制策略开发

汽车工程, 2019, 41(1):50-56

[本文引用: 2]

Zhao Weiqiang, Ling Jinpeng, Zong Changfu.

Development of anti-rollover control strategy for liquid tank semi-trailer

Automotive Engineering, 2019, 41(1):50-56 (in Chinese)

[本文引用: 2]

任园园, 李显生, 郑雪莲 等.

液罐车精确动力学建模及其侧倾稳定性

上海交通大学学报, 2020, 54(3):312-321

[本文引用: 2]

Ren Yuanyuan, Li Xiansheng, Zheng Xuelian, et al.

Accurate dynamics modeling and roll stability of tank vehicle

Journal of Shanghai Jiao Tong University, 2020, 54(3):312-321 (in Chinese)

[本文引用: 2]

李伟建.

罐式半挂车侧倾稳定性分析与防侧翻控制研究. [博士论文]

长春: 吉林大学, 2020

[本文引用: 1]

Li Weijian.

Research on stability analysis and anti-rollover control of tank semi-trailer. [PhD Thesis]

Changchun: Jilin University, 2020 (in Chinese)

[本文引用: 1]

于迪, 李显, 刘宏飞 等.

非满载液罐车侧倾稳定性模型研究

湖南大学学报(自然科学版), 2016, 43(8):40-44

[本文引用: 1]

Yu Di, Li Xian, Liu Hongfei, et al.

Research on roll stability model of partially-filled tankers

Journal of Hunan University $($Natural Sciences$)$, 2016, 43(8):40-44 (in Chinese)

[本文引用: 1]

陈益苞, Subhash Rakhej, 上官文斌.

罐体横截面形状对液罐车侧倾稳定性影响分析

振动与冲击, 2016, 35(6):146-151

[本文引用: 1]

Chen Yibao, Subhash Rakhej, Shangguan Wenbin.

Modified design and safety analysis of tank cross section based on roll stability

Journal of Vibration and Shock, 2016, 35(6):146-151 (in Chinese)

[本文引用: 1]

沈钰杰, 陈龙, 杨晓 等.

应用惯容器提升车辆侧向稳定性的研究

汽车工程, 2018, 40(6):693-698

[本文引用: 1]

Shen Yujie, Chen Long, Yang Xiao, et al.

A research on the enhancement of vehicle lateral stability by applying inerter to suspension

Automotive Engineering, 2018, 40(6):693-698 (in Chinese)

[本文引用: 1]

/

〈 〉