本文提出一种基于麻雀搜索算法(sparrow search algorithm, SSA)优化BP神经网络的预测冻胀率模型,并结合多种优化方法提高预测精度,加快收敛速度,在此基础上研究人工冻土冻胀率影响因素敏感性。
1 人工冻土冻胀率预测
1.1 冻胀率试验
对甘肃地区三种不同性质土体进行冻胀率试验,土体物理化学性质见文献[4],采用外部补水的单向冻结方法。试验仪器主要包括保温系统、供水系统、温控系统、变形测量系统。在初始含水量、初始干重度、冻结速率、地下水位埋深、塑性指标、总离子含量范围给定情况下进行试验。由于文章使用小样本预测冻胀率,将各类不同性质土体分别试验,塑性指数$I_{\rm P}$和盐离子含量$S$是土体的自身特性,在同类型土中不属于变量,所以选取初始含水量、初始干重度、冻结速率、地下水位为输入量。考虑到我国以冻胀率来表示土体的冻胀敏感性,选择冻胀率为输出量。
1.2 SSA-BP网络
SSA是近年来新提出的一种种群优化算法。是将麻雀种群中个体分为生产者与拾荒者,以种群的采食与反捕食为基础设计的一种新型优化算法,具有较高的收敛性能和局部搜索能力[15]。SSA-BP神经网络主要是对权值和阈值的优化,用SSA的最优状态值来替代BP神经网络里面的初始权值和初始阈值,减少迭代次数,使网络更快满足设计要求。
使用SSA-BP网络预测土体冻胀率影响因素敏感性的基本步骤如下。
(1) 导入试验数据,对数据进行预处理;
(2) 设置SSA-BP网络参数;
(3) 使用SSA-BP网络进行训练、测试、预测;
(4) 导出训练好的权值、阈值矩阵;
(5) 分别计算
$p_{ij} =\frac{w_{ij} }{\sum\limits_{j=1}^m {w_{ij} }},\ \ q_{i} =\frac{w_{i} }{\sum\limits_{i=1}^n {w_{i} } };$
式中,$w_{ij}$为输入层第$j$个节点与隐含层第$i$个节点的连接权值,$w_{i}$为隐含层第$i$个节点与输出量的连接权值,$m$为输入层节点数,$n$为隐含层节点数。$p_{ij}$为$w_{ij}$与隐含层第$i$个节点相关联的全部输入层连接权值和的比值,$q_{i}$为$w_{i}$与输出量相关联的全部隐含层连接权值和的比值。
(6) 计算影响因素敏感性$K_{j} =\sum\limits_{i=1}^n {q_{i}^{p_{ij} }}$。
1.3 网络模型参数的选择
由于单隐含层的拓扑结构适用于绝大多数条件下的非线性拟合,所以选用输入层—隐含层—输出层的三层网络拓扑结构。隐含层节点个数通常用$S=\sqrt{M+N} +a$确定,其中$S$为隐含层节点数,$M$为输入层节点数,$N$为输出层节点数,$a$为1~10之间的整数值。为了使预测更精准,将$a$值选择范围从10扩大至20,编写代码循环运行,选择误差最小的隐含层节点数进行预测。
结合试验数据确定传递函数分别为对数S型传递函数和纯线性函数,并且通过多次尝试选取Levenberg-Marguardt BP训练函数使误差减小。影响BP神经网络预测精度的重要参数是学习速率$\eta$和动量因子$\alpha $,学习速率$\eta $过小则收敛速率过慢、$\eta$过大容易修正过度而导致振荡发散。动量因子$\alpha$过大存在丢失最小值风险,$\alpha$较小可以避免局部极小值,但会使训练时间增加。使用二分法筛选发现$\eta$和$\alpha $值均选为0.01时误差最小。\vspace{-.5mm}
1.4 SSA-BP神经网络模型的训练
表1 训练集的试验值、训练值和训练误差
Table 1
 |
1.5 SSA-BP神经网络模型的结果分析
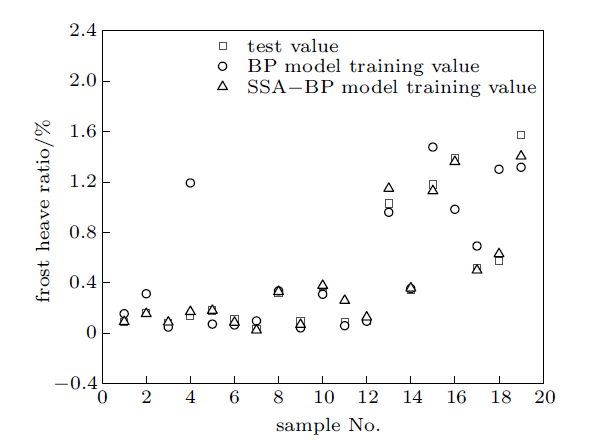
图1为砂壤土两种网络预测模型训练集的试验值与预测值对比散点图,结果显示SSA-BP神经网络模型与实际值的拟合效果更优。
图1
图1
两种网络预测模型训练集的试验值与预测值
Fig.1
Experimental and predicted values for the training set of two network prediction models
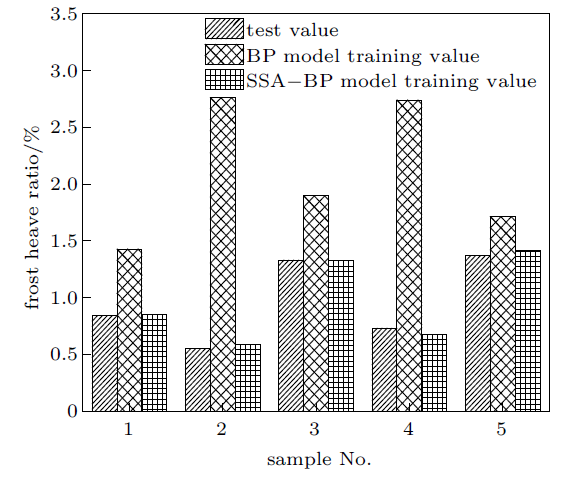
从图2砂壤土的试验值与预测值对比图中可以清晰看出,在使用SSA-BP神经网络模型预测中样本4的预测误差最大,达到$-$0.052 6,其余四个预测误差均在[-0.04,0.04]之间。较传统BP神经网络精度至少提升十倍。SSA-BP模型预测评价指标均方误差根为0.034 971,较BP模型均方误差根1.393 4提升巨大,并且平均绝对百分比误差从BP模型的162.96%降至3.81%,SSA-BP模型优化效果显著。
图2
图2
砂壤土预测模型的试验值与预测值
Fig.2
Test and predicted values of sandy loam prediction model
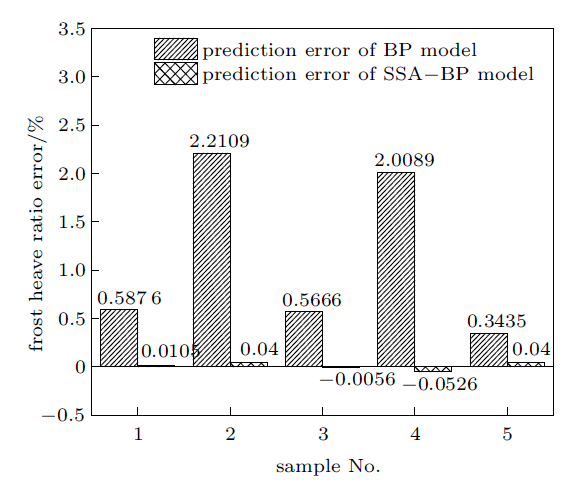
由图3可知砂壤土使用SSA-BP神经网络预测模型进行预测时,误差较传统BP神经网络优化效果明显。砂壤土预测模型的误差整体控制在$[-0.06, 0.04]$之间,远小于$[-0.5,0.5]$,优化效果显著。
图3
图4
图5
2 冻胀率影响因素敏感性分析
2.1 影响因素敏感性定义
影响因素敏感性通过定义无量纲形式的敏感性函数,使多个影响因素敏感性分析具有了可比性[16]。传统做法是设定一个基准状态,各影响因素取定值。再单独对各影响因素在取值范围内进行波动,观测结果波动程度及趋势。
神经网络模型中权值矩阵可以表明各个输入变量的敏感性大小,但需要综合考虑网络拓扑结构、归一化范围、激活函数等因素,过于繁琐。尝试将敏感性由权值矩阵简化为各影响因素权值占比,便于直观查看各个因素对冻胀率影响程度即影响因素敏感性$K_{j}=\sum\limits_{i=1}^n {q_{i}^{p_{ij} }} $。
2.2 影响因素敏感性公式的应用
工程实例中地下水位$H_{\rm w}$范围为0.43~0.95 m,初始含水率$W$范围为12.17%~28.6%,初始干容重$\gamma_{\rm d}$范围为1.35~1.61 g/cm$^{3}$,冻结速率$V_{\rm f}$范围为2.95~ 9.68 cm/d。
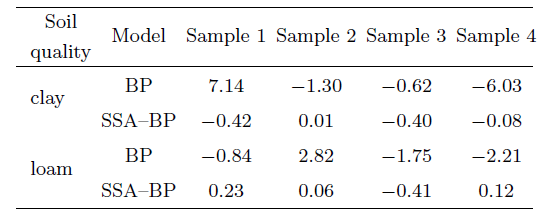
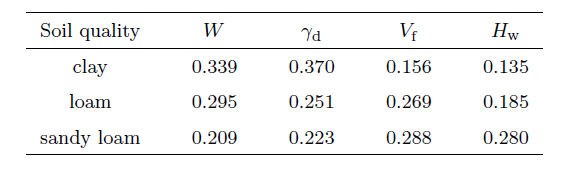
应用SSA-BP神经网络对甘肃地区三种土质建立三个独立预测模型,根据上述定义,计算各模型中因素对人工冻土敏感性$K_{i}$,如表4。
由表4可知,冻胀率各影响因素敏感性中初始含水率的占比,在黏土、壤土与砂壤土中依次降低。土体冻胀的过程也是土中气态、液态水向冰转变的过程,在试验中黏土的塑限指数最大即初始含水量在塑限含水量与液限含水量之间试样最多,壤土和砂壤土塑限指数依次降低,与计算结果吻合。
黏土中初始含水量与初始干容重敏感性占比超过70%是影响冻胀的主要因素,在人工冻土施工中可以外部控制水量和施加外部载荷降低冻胀率。壤土中初始含水量、冻结速率、初始干容重、地下水位线敏感性依次降低,初始含水量敏感性最大。影响砂壤土冻胀率的各因素中,冻结速率与地下水位线的影响超过一半,在工程中可以通过改变冻结温度和外部补水量来减少冻胀率。
综上可知,相同影响因素在不同土质中的敏感性不同,受土体的土质影响较大。
3 结论
本文使用SSA-BP神经网络进行土体冻胀率预测,以甘肃地区土体冻胀率为例。选用影响试样冻胀率的四个主要参数即初始含水率、初始干容重、冻结速率、地下水位作为输入层,冻胀率为输出层,构建了三层SSA-BP神经网络拓扑结构,得到以下结论。
(1) 基于麻雀搜索算法优化权值与阈值,提高了BP神经网络模型预测精度。对砂壤土、黏土、壤土的预测平均绝对误差均方误差根均小于0.3,较BP神经网络预测提升至少十倍。小样本预测针对不同土质均取得较好的预测结果,表明在寒区施工时为了减少冻害的影响,可以取试样进行试验获取参数,使用SSA-BP神经网络进行预测,为工程安全高效施工提供一种选择的方案。
(2) 提出新的影响因素敏感性公式,将各影响因素敏感性从神经网络繁杂的权值矩阵和阈值矩阵简化为数值。对砂壤土、壤土、黏土进行土体冻胀率敏感性分析,最敏感的影响因素分别是冻结速率、初始含水率、初始干容重,并且冻结速率、地下水位对不同土质冻胀率敏感性与土质塑限指数排序成反比。工程应用中,可根据不同实际情况采取针对措施减少冻胀危害。
参考文献
Effect of penetration rate of freezing and confining stress on the frost heave ratio of soil
寒区公路隧道冻胀力荷载的分布形式和简化计算方法
Distribution and simplified calculation method of the frost heaving force of highway tunnels in cold regions
齐齐哈尔地区粉质黏土冻胀特性试验研究
Experimental study on frost heaving characteristics of silty clay in Qiqihar region
Modelling of shearing behaviour of a residual soil with recurrent neural network
基于级连相关神经网络的人工冻土本构模型
Constitutive model of artificial frozen soil based on cascade-correlation neural network
基于ANN的碳纤维楠竹锚杆锚固力预测研究
Anchorage force prediction for the CFRP-bamboo bolt based on artificial neural network
因子分析-概率神经网络模型在边坡稳定性评价中的应用
Application of factor analysis and probabilistic neural network model on evaluation of the slope stability
基于集成学习与径向基神经网络耦合模型的三峡库区滑坡易发性评价
Landslide susceptibility assessment by applying the coupling method of radial basis neural network and adaboost: a case study from the three gorges reservoir area
优化GM(1,1)与SVM组合模型的路基冻胀预测应用
The forecast application of subgrade's frost-heaving index based on optimized GM(1,1) and SVM combination model
红砂岩单轴压缩宏细观参数映射关系研究
Macro and microscopic parameter mapping relationship for red sandstone
基于BP神经网络和FEFLOW模型模拟预测多年冻土活动层温度——以青藏高原风火山地区为例
Simulation and prediction of permafrost active layer temperature based on BP neural network and FEFLOW model: take the Fenghuoshan area on the Tibetan Plateau as an example
基于PCA-BP神经网络的审计风险识别研究
The research of audit risk identification based on PCA and BP neural network
Václav S. Metaheuristic design of feedforward neural networks: a review of two decades of research
A novel swarm intelligence optimization approach: sparrow search algorithm