膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土。由于其对环境湿热变化敏感,性质极不稳定。按黏土矿物分类,可以将膨胀土归纳为两大类。一类以蒙脱石为主;另一类以伊利石土和高岭土为主。按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1 ] 。土壤膨胀变形受初始含水量[2 ] 以及自重应力[3 ] 的影响,具有明显的非线性流变特征[4 -5 ] ,并且膨胀力和膨胀变形随土壤增湿程度增加而增加。在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象。不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题。因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义。
吸附性可以解析地定义为土壤含水量和扩散系数的函数。研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散。因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] 。近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下。陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性。曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程。王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构。Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程。随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解。Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性。张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型。基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程。
需要指出的是,膨胀土受干湿循环过程的影响,土壤颗粒会不同程度地膨胀或收缩。对于膨胀性土壤,使用经典的固定坐标是不合适的。本文考虑引入物质坐标[15 ] 作为描述膨胀性介质吸附过程的媒介。达西定律描述了流体相对于相对不动的黏土颗粒的流动,该物质坐标理论是基于参考黏土质量分布而定义的长度标度,而不是传统的固定长度标度而发展而来的[23 ] 。物质坐标反映固体土壤颗粒的体积与水分的体积之间的关系,通过含水率在垂向的积分体现。物质坐标是含水率和空间位置坐标的函数,通过在垂直方向上积分可以计算出含水率累积吸附量,是描述膨胀土累积吸附的有效工具。因此,本文将基于物质坐标下的分形导数模型,描述膨胀性土壤中水分的累积吸附过程。
1 分形导数累积吸附模型
1.1 物质坐标与分形导数
物质坐标不是基于传统的长度标度,而是基于由吸附剂质量分布定义的长度标度,或者当系统内总质量恒定时,根据两个互扩散组分的质量分布而定义的[23 ] 。考虑到膨胀土壤的特性,采用物质坐标描述其膨胀性。膨胀性介质的物质坐标定义为[24 ]
(1) $ m=\int_0^{z_{1}} \left( 1+e \right)^{-1}{\rm d}z $
其中$z$为垂直方向上通常的空间坐标,$e$为孔隙比,$e={\vartheta}/({1-\vartheta})$,$\vartheta ={\vartheta_{{\rm l}}}/{\vartheta_{{\rm s}}}$为含水率,$\vartheta_{{\rm l}}$和$\vartheta_{{\rm s}}$分别为液体和固体的体积分数[25 -26 ] 。
(2) $ I\left( t \right)=\int m {\rm d}\vartheta $
(3) $ \frac{{\rm d}\vartheta }{{\rm d}{t}^{{\alpha }}} =\frac{\vartheta \left( t \right)-\vartheta \left(t_{1}\right)}{(t-t_{0})^{\alpha}-(t_{1}-t_{0})^{\alpha}} =\frac{1}{\alpha(t-t_{0})^{\alpha-1}}\frac{{\rm d}\vartheta }{{\rm d}t} $
(4) $ \frac{{\rm d}\vartheta }{{\rm d}t^{\alpha }} =\frac{\vartheta\left( t \right)-\vartheta \left( t_{1} \right)}{t^{\alpha }-t_{1}^{\alpha }} =\frac{1}{\alpha t^{\alpha {\rm -1}}}\frac{{\rm d}\vartheta }{{\rm d}t} $
(5) $ \frac{{\rm d} m}{{\rm d} x^{\beta}}=\lim _{x \rightarrow x^{\prime}} \frac{m(x)-m(x')}{x^{\beta}-x'^{\beta}}=\frac{1}{\beta x^{\beta-1}} \frac{{\rm d} m}{{\rm d} x} $
式(3)~式(5)中的$\alpha $和$\beta$分别为时间和空间分形导数的阶数,可以描述粒子运动的分形轨迹,描述介质的空间分形维数。构建分形导数扩散方程时[15 ] ,通常采用的分形导数为
(6) $ \frac{\partial p\left( x,t \right)}{\partial t^{\alpha}} =\frac{p\left( x,t \right)-p\left(x,t_{1} \right)}{t^{\alpha}-t_{1}^{\alpha }} $
(7) $ \frac{p(x, t)}{\partial x^{\beta}}=\lim _{x_{1} \rightarrow x} \frac{p(x, t)-p\left(x_{1}, t\right)}{x^{\beta}-x_{1}^{\beta}} $
其中$p(x,t)$是时刻$t$下,空间位置$x$对应的粒子浓度。
(8) $ \left. \begin{array}{*{20}c} t^{\alpha } =\hat{t}\\ x^{\beta } =\hat{x}\\ \end{array} \right\} $
(9) $ \frac{\partial p\left( x,t \right)}{\partial\hat{t}} =D_{\alpha,\beta }\hat{\nabla}^{2}p\left( x,t \right) $
其中,$D_{\alpha,\beta }$为扩散系数,$\hat{\nabla }^{2}$是坐标$\hat{x}$下的拉普拉斯算子,其基本解为
(10) $ p\left( x,t \right) =\frac{1}{\sqrt {4\pi D_{\alpha,\beta }\hat{t}}}{\rm e}^{-\frac{\hat{x}^{2}}{4D_{\alpha,\beta }\hat{t}}} $
(11) $ p(x,t)=\frac{1}{\sqrt {4\pi D_{\alpha,\beta }\hat{t}^{\alpha }} }{\rm e}^{-\hat{x}^{2\beta }/(4D_{\alpha,\beta }\hat{t}^{\alpha })} $
当$\alpha =1$,$\beta=1$时,式(11)退化为高斯分布。时空分形导数扩散模型对应粒子的均方位移为[18 ]
(12) $ \left\langle x^{2}\left( t \right) \right\rangle \sim t^{\frac{3\alpha -\alpha \beta }{2\beta }} $
1.2 膨胀性土壤累积吸附的分形导数模型
根据物质坐标,建立膨胀性土壤中水分吸附的时间分形导数扩散波动模型。物质坐标下的分形导数扩散波动方程为
(13) $ \frac{\partial \vartheta }{\partial t^{\alpha }} =\frac{\partial }{\partial m}\left( D_{m}\frac{\partial \vartheta }{\partial m} \right) $
其中$\alpha (0<\alpha \leqslant 2)$为时间分形导数的阶数。$1<\alpha \leqslant 2$表征快吸附,$0<\alpha <1$为慢吸附,$\alpha=1$时为正常吸附;$D_{m}$为扩散系数,cm$^{2}$/h。初值条件为$\vartheta =\vartheta_{i}$,$t=0$,$m>0$,边界条件为$\vartheta =\vartheta_{0}f\left( t\right)$,$t>0$,$m=0$;$\vartheta\to 0$,$m\to \infty$。其中$f\left( t\right)$为时间依赖的函数,$\vartheta_{0}$为土壤表面含水率,$\vartheta_{i}$为初始含水率。
(14) $ \vartheta =\frac{1}{\sqrt {4\pi D_{m}t^{\alpha }} }\exp \left( -\frac{m^{2}}{4D_{m}t^{\alpha }} \right) $
(15) $ m =\sqrt {{\rm -4}D_{m}t^{\alpha }\ln {(\sqrt{4\pi D_{m}t^{\alpha }} }\vartheta } ) $
结合式(2)和式(15),推导分形导数模型对应膨胀性土壤中的累积吸附量
(16) $ I(t)=\int_{\vartheta_{i}}^{\vartheta_{0}} \sqrt{-4D_{m}t^{\alpha }\ln (\sqrt {4\pi D_{m}t^{\alpha }} \vartheta )} {\rm d}\vartheta $
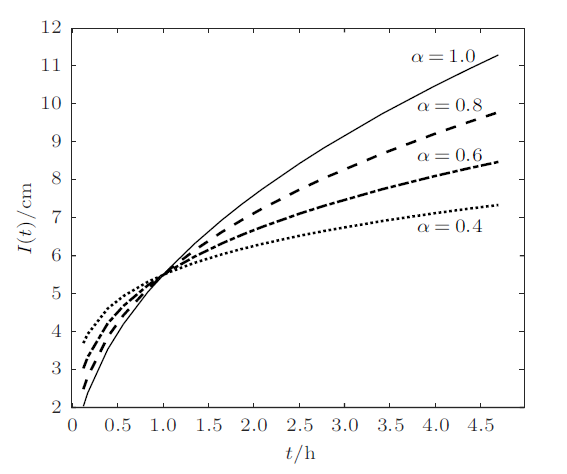
图1 给出了式(16)中不同时间分形导数的阶数($\alpha =0.4$,0.6,0.8,1.0),$D_{m}=1$ cm$^{2}$/h,$\vartheta_{i}=0.000 1$和$\vartheta_{0}=0.000 2$对应的累积吸附曲线。由图1 可见,$\alpha$的值越小,累积吸附量增长得越慢。
图1
图1
分形导数模型的不同阶数$\alpha =0.4$,0.6,0.8,1.0对应的累积吸附曲线
Fig.1
Curves of cumulative adsorption for $\alpha =0.4$,0.6, 0.8,1.0 in the fractal derivative model
需要指出的是,传统模型即整数阶模型,对应膨胀性土壤中水分累积吸附量的表达式为
(17) $I\left( t \right) =S{\rm \cdot }t^{{\rm 1/2}}$
式中,$S$为土壤渗吸率,cm/h$^{1/2}$。
2 分形导数模型应用与验证
2.1 膨胀性黑土中累积吸附过程应用实例
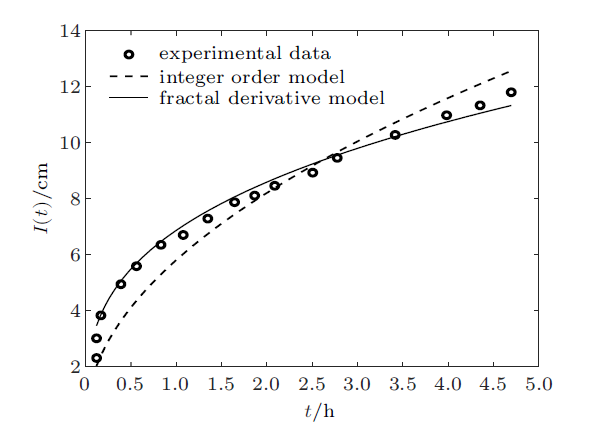
该实验中使用的膨胀性土壤为0.5~1.0 mm的黑土表层团聚体对应的累积吸附数据[29 ] 。实验中使用了直径为5.09 cm,长为90 cm的有机玻璃柱,其结构类似于土柱。入渗测量采用与土柱相同的方式进行,随着入渗的进行,张力计元件插入湿润锋后面。当柱底出现毛细管条纹并达到稳态流动时,实验终止。由此,在水流达到稳定之前,可以得到入渗水分随着时间的累积吸附曲线。
分别采用分形导数模型和整数阶模型,即式(16)和式(17)拟合黑土中的水分累积吸附量,其中$\vartheta_{0}=0.04$,$\vartheta_{i}=0.32$。运用非线性最小二乘法估计模型的参数,并计算均方根误差,计算公式为
(18) $ RMSE\left( I,n \right) =\sqrt{\frac{1}{n}\sum\nolimits_i^n{(I_{1}-I_{0})^{2}}} $
其中$I_{1}$为拟合结果,$I_{0}$为实际累积吸附,$n$为数据个数。
得到分形导数模型的参数$\alpha=0.87$,表明水分在黑土中的吸附过程为慢吸附。土壤扩散系数$D_{m}=43.12$ cm$^{2}$/h,模拟结果的均方根误差$e_{0}=0.002 7$。整数阶模型的土壤渗吸率$S=5.80$ cm/h$^{1/2}$,均方根误差$e_{0}=1.264 9$。图2 给出了整数阶以及分形导数模型累积吸附$I-t$的对比曲线。由图2 可知,由于膨胀性土壤在扩散前期具有较强的吸附性,随着吸附量逐渐增加,土壤吸附水分的速率也逐渐放缓,分形导数模型在预测膨胀性土壤中水分累积吸附变化过程上具有明显的优势,均方根误差较小。
图2
图2
分形导数模型和整数阶模型拟合黑土中水分累积吸附量的曲线图
Fig.2
Plots of cumulative adsorption capacity of water in black soil by usingthe fractal derivative model and integer order model
2.2 砂土中累积吸附的应用实例
对比研究选用膨胀性不明显的砂土累积吸附实验[29 ] 。结合水分在砂土中累积吸附的实验数据,用上述类似的方法处理实验数据,拟合得到分形导数模型累积吸附方程中最合适的匹配参数,参数的值为:$\alpha=1.91$,$D_{m}=36.37$ cm$^{2}$/h,均方根误差$e_{1}=0.004 8$。整数阶模型的土壤渗吸率$S=6.80$ cm/h$^{1/2}$,均方根误差$e_{0}=2.174 7$。图3 给出了整数阶以及分形导数模型对应累积吸附量$I-t$的对比曲线。由图3 可知,对于砂土中的水分吸附过程,分形导数模型在时间分形尺度上与传统的整数阶导数模型相比具有较好的拟合效果。并且时间分形导数模型的阶数大于1表明水分在此种砂土中的累积吸附为快吸附,膨胀性不明显。
图3
图3
分形导数模型和整数阶模型拟合砂土中水分累积吸附量的曲线图
Fig.3
Plots of cumulative adsorption of water in the sand by using the fractal derivative model and integer order model
3 结论
本文基于物质坐标建立了膨胀土中水分吸附的分形导数模型,推导了膨胀性土壤累积吸附与时间的关系,其中时间分形导数模型的阶数能够表征水分在膨胀性土壤中扩散类型,并表征介质的非均质性。通过两个实例,观察到膨胀性土壤具有较明显的吸附特征,其累积吸附对应分形导数阶数的值小于1,表明黑土的吸附过程为慢吸附。砂土累积吸附对应分形导数阶数的值大于1,基本不考虑其吸附力作用。此外膨胀性土壤的累积吸附系数也是反映土壤结构特征的另一个重要指标,需要与分形导数模型的阶数同时考虑,其相关性还需要进一步研究。
通过上述实验,验证了分形导数模型的可行性,并且可以得到分形导数模型在描述膨胀性土壤反常吸附过程较传统整数阶导数模型的优势,分形导数的拟合精度较高,能够较为全面地表征和预测累积吸附的演化规律,并能够对膨胀性土壤的吸附过程进行分类。需要指出的是,对于文献[19 ] 提出的物质坐标下的分数阶导数模型,采用的是分数阶导数非局部算子,对应的物质坐标是无穷级数的形式。为方便计算,仅采用无穷级数的前两项推导得到了累积吸附的表达式,该累积吸附为时间的幂函数,其中分数阶导数的阶数为1时,退化为正常吸附。该简化方法降低了分数阶导数模型的精度。而物质坐标下的分形导数模型则不存在此问题。本文的工作为地下土体环境污染的治理和修复提供了新的理论参考。后续将结合不同类型的膨胀性土壤水分以及溶质的吸附实验,验证和推广本文的工作。
参考文献
View Option
[10]
Sun HG Meerschaert MM Zhang Y , et al . A fractal Richards' equation to capture the non-Boltzmann scaling of water transport in unsaturated media
Advances in Water Resources 2013 , 52 :292 -295
DOI
URL
[本文引用: 1]
[11]
Lin GX . An effective phase shift diffusion equation method for analysis of PFG normal and fractional diffusions
Journal of Magnetic Resonance 2015 , 259 :232 -240
DOI
URL
[12]
Reyes-Marambio J Moser F Gana F , et al . A fractal time thermal model for predicting the surface temperature of air-cooled cylindrical lion cells based on experimental measurements
Journal of Power Sources 2016 , 306 :636 -645
DOI
URL
[13]
Balamlin AS Boryreyes J Shapiro M , Towards a physics on fractals: differential vector calculus in three dimensional continuum with fractal metric
Physica A 2016 , 444 :345 -359
DOI
URL
[14]
Hu ZH Tu XK . A new discrete economic model involving generalized fractal derivative
Advances in Difference Equations 2015 , 1 :1 -11
[15]
Chen W . Time-space fabric underlying anomalous diffusion
Chaos, Solitons & Fractals 2006 , 28 (4 ):923 -929
[本文引用: 4]
[16]
陈文 , 梁英杰 , 杨旭 . 基于Hausdorff分形导数Richards方程的土壤入渗率和水文模型类型
应用数学和力学 , 2018 , 39 (1 ):77 -82
[本文引用: 1]
Chen Wen Liang Yingjie Yang Xu . Soil infiltration rates and hydrology model classifications based on the Hausdorfffractal derivative Richards' equation
Applied Mathematics and Mechanics 2018 , 39 (1 ):77 -82 (in Chinese)
[本文引用: 1]
[17]
曲艺 , 孙洪广 , 李志鹏 . 分形结构中介质渗透性对扩散过程的影响
科学技术与工程 , 2019 , 19 (7 ):15 -19
[本文引用: 1]
Qu Yi Sun Hongguang Li Zhipeng . The influence of medium permeability on diffusion process in fractal structure
Science Technology and Engineering 2019 , 19 (7 ):15 -19 (in Chinese)
[本文引用: 1]
[18]
王书鸿 , 梁英杰 . 交联葡聚糖凝胶中反常扩散的Hausdorff分形导数扩散成像模型
力学季刊 , 2020 , 41 (4 ):666 -673
[本文引用: 2]
Wang Shuhong Liang Yingjie . Hausdorff fractal derivative diffusion imaging model for anomalous diffusion in sephadex gel
Chinese Quarterly of Mechanics 2020 , 41 (4 ):666 -673 (in Chinese)
[本文引用: 2]
[1]
全明 . 膨胀土的分类及膨胀土地区基础的施工方案
水泥技术 , 2021 (1 ):73 -80
[本文引用: 1]
Quan Ming . Classification of expansive soil and construction scheme of foundations in expansive soil area
Cement Technology 2021 (1 ):73 -80 (in Chinese)
[本文引用: 1]
[2]
张春晓 , 肖宏彬 , 包嘉邈 等 . 膨胀土应力松弛的分数阶模型
岩土力学 , 2018 , 39 (5 ):1747 -1760
[本文引用: 1]
Zhang Chunxiao Xiao Hongbin Bao Jiamiao , et al . Stress relaxation model of expansive soils based on fractional calculus
Rock and Soil Mechanics 2018 , 39 (5 ):1747 -1760 (in Chinese)
[本文引用: 1]
[19]
Su N . Equations of anomalous absorption onto swelling porous media
Materials Letters 2009 , 63 (28 ):2483 -2485
DOI
URL
[本文引用: 2]
[20]
Su N . Theory of infiltration: infiltration into swelling soils in a material coordinate
Journal of Hydrology 2010 , 395 (1 ):103 -108
DOI
URL
[本文引用: 1]
[3]
甘永德 , 刘欢 , 贾仰文 等 . 膨胀性土壤饱和水分运动参数计算模型
工程科学与技术 , 2018 , 50 (2 ):77 -83
[本文引用: 1]
Gan Yongde Liu Huan Jia Yangwen , et al . Swelling soil saturated water movement parameters calculating models
Engineering Science and Technology 2018 , 50 (2 ):77 -83 (in Chinese)
[本文引用: 1]
[4]
金文婷 , 肖宏彬 . 南宁膨胀土剪切蠕变特性及流变模型研究
公路工程 , 2011 , 36 (6 ):64 -69, 77
[本文引用: 1]
Jin Wenting Xiao Hongbin . Experimental study on shear creep characteristic and rheological model of Nanning expansive soils
Highway Engineering 2011 , 36 (6 ):64 -69, 77 (in Chinese)
[本文引用: 1]
[21]
Voller VR . A direct simulation demonstrating the role of special heterogeneity in determining anomalous diffusive transport
Water Resources Research 2015 , 51 (4 ):2119 -2127
DOI
URL
[本文引用: 1]
[22]
张东辉 , 施明恒 , 金峰 等 . 分形多孔介质的粒子扩散特点
工程热物理学报 , 2004 , 25 (5 ):825 -827
[本文引用: 1]
[5]
李珍玉 , 肖宏彬 , 金文婷 等 . 南宁膨胀土非线性流变模型研究
岩土力学 , 2012 , 33 (8 ):2297 -2302
[本文引用: 1]
Li Zhenyu Xiao Hongbin Jin Wenting , et al . Study of nonlinear rheological model of Nanning expansive soils
Rock and Soil Mechanics 2012 , 33 (8 ):2297 -2302 (in Chinese)
[本文引用: 1]
[6]
刘伟 , 范爱武 , 黄晓明 . 多孔介质传热传质理论与应用 . 北京 : 科学出版社 , 2006
[本文引用: 1]
[7]
Mukhopadhyay S Cushman JH . Diffusive transport of volatile pollutants in nonaqueous-phase liquid contaminated soil: a fractal model
Transport in Porous Media 1998 , 30 (2 ):125 -154
DOI
URL
[8]
陈文 , 孙洪广 , 李西成 . 力学与工程问题的分数阶导数建模 . 北京 : 科学出版社 , 2010
[本文引用: 1]
[9]
Liang YJ Chen W Magin RL . Connecting complexity with spectral entropy using the Laplace transformed solution to the fractional diffusion equation
Physica A 2016 , 453 :327 -335
DOI
URL
[本文引用: 1]
[22]
Zhang Donghui Shi Mingheng Jin Feng , et al . Diffusion characteristic in fractal porous media
Journal of Engineering Thermophysics 2004 , 25 (5 ):825 -827 (in Chinese)
[本文引用: 1]
[23]
Smiles DE Rosenthal Margaret J . The movement of water in swelling materials
Soil Research 1968 , 6 :237 -248
DOI
URL
[本文引用: 2]
[24]
Karalis TK . Mechanics of Swelling
Berlin:Springer-Verlag , 1992
[本文引用: 1]
[25]
Philip JR Smiles DE . The steady-state measurement of the relation between hydraulic conductivity and moisture content in soils
Water Resources Research 1968 , 5 :1029 -1030
[本文引用: 1]
[26]
Smiles DE . Hydrology of Swelling Clay Soils. Encyclopedia of Hydrological Sciences
Chichester: Wiley , 2005
[本文引用: 1]
[27]
Smith RE . Infiltration Theory for Hydrologic Applications
Washington, DC: American Geophysical Union , 2002
[本文引用: 1]
[28]
Stockdale A Banwart S . Recovery of technologically critical lanthanides from ion adsorption soils
Minerals Engineering 2021 , 168 :1069 21
[本文引用: 1]
[29]
Bridge BJ . An experimental study of vertical infiltration into a structurally unstable swelling soil, with particular reference to the infiltration throttle
Soil Research 1973 , 11 (2 ):121 -132
DOI
URL
[本文引用: 2]
A fractal Richards' equation to capture the non-Boltzmann scaling of water transport in unsaturated media
1
2013
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
An effective phase shift diffusion equation method for analysis of PFG normal and fractional diffusions
0
2015
A fractal time thermal model for predicting the surface temperature of air-cooled cylindrical lion cells based on experimental measurements
0
2016
Towards a physics on fractals: differential vector calculus in three dimensional continuum with fractal metric
0
2016
A new discrete economic model involving generalized fractal derivative
0
2015
Time-space fabric underlying anomalous diffusion
4
2006
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
... 需要指出的是,膨胀土受干湿循环过程的影响,土壤颗粒会不同程度地膨胀或收缩.对于膨胀性土壤,使用经典的固定坐标是不合适的.本文考虑引入物质坐标[15 ] 作为描述膨胀性介质吸附过程的媒介.达西定律描述了流体相对于相对不动的黏土颗粒的流动,该物质坐标理论是基于参考黏土质量分布而定义的长度标度,而不是传统的固定长度标度而发展而来的[23 ] .物质坐标反映固体土壤颗粒的体积与水分的体积之间的关系,通过含水率在垂向的积分体现.物质坐标是含水率和空间位置坐标的函数,通过在垂直方向上积分可以计算出含水率累积吸附量,是描述膨胀土累积吸附的有效工具.因此,本文将基于物质坐标下的分形导数模型,描述膨胀性土壤中水分的累积吸附过程. ...
... 时间分形导数的一般表达式[15 ] 为 ...
... 式(3)~式(5)中的$\alpha $和$\beta$分别为时间和空间分形导数的阶数,可以描述粒子运动的分形轨迹,描述介质的空间分形维数.构建分形导数扩散方程时[15 ] ,通常采用的分形导数为 ...
基于Hausdorff分形导数Richards方程的土壤入渗率和水文模型类型
1
2018
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
基于Hausdorff分形导数Richards方程的土壤入渗率和水文模型类型
1
2018
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
分形结构中介质渗透性对扩散过程的影响
1
2019
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
分形结构中介质渗透性对扩散过程的影响
1
2019
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
交联葡聚糖凝胶中反常扩散的Hausdorff分形导数扩散成像模型
2
2020
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
... 当$\alpha =1$,$\beta=1$时,式(11)退化为高斯分布.时空分形导数扩散模型对应粒子的均方位移为[18 ] ...
交联葡聚糖凝胶中反常扩散的Hausdorff分形导数扩散成像模型
2
2020
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
... 当$\alpha =1$,$\beta=1$时,式(11)退化为高斯分布.时空分形导数扩散模型对应粒子的均方位移为[18 ] ...
膨胀土的分类及膨胀土地区基础的施工方案
1
2021
... 膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土.由于其对环境湿热变化敏感,性质极不稳定.按黏土矿物分类,可以将膨胀土归纳为两大类.一类以蒙脱石为主;另一类以伊利石土和高岭土为主.按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1 ] .土壤膨胀变形受初始含水量[2 ] 以及自重应力[3 ] 的影响,具有明显的非线性流变特征[4 -5 ] ,并且膨胀力和膨胀变形随土壤增湿程度增加而增加.在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象.不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题.因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义. ...
膨胀土的分类及膨胀土地区基础的施工方案
1
2021
... 膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土.由于其对环境湿热变化敏感,性质极不稳定.按黏土矿物分类,可以将膨胀土归纳为两大类.一类以蒙脱石为主;另一类以伊利石土和高岭土为主.按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1 ] .土壤膨胀变形受初始含水量[2 ] 以及自重应力[3 ] 的影响,具有明显的非线性流变特征[4 -5 ] ,并且膨胀力和膨胀变形随土壤增湿程度增加而增加.在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象.不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题.因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义. ...
膨胀土应力松弛的分数阶模型
1
2018
... 膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土.由于其对环境湿热变化敏感,性质极不稳定.按黏土矿物分类,可以将膨胀土归纳为两大类.一类以蒙脱石为主;另一类以伊利石土和高岭土为主.按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1 ] .土壤膨胀变形受初始含水量[2 ] 以及自重应力[3 ] 的影响,具有明显的非线性流变特征[4 -5 ] ,并且膨胀力和膨胀变形随土壤增湿程度增加而增加.在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象.不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题.因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义. ...
膨胀土应力松弛的分数阶模型
1
2018
... 膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土.由于其对环境湿热变化敏感,性质极不稳定.按黏土矿物分类,可以将膨胀土归纳为两大类.一类以蒙脱石为主;另一类以伊利石土和高岭土为主.按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1 ] .土壤膨胀变形受初始含水量[2 ] 以及自重应力[3 ] 的影响,具有明显的非线性流变特征[4 -5 ] ,并且膨胀力和膨胀变形随土壤增湿程度增加而增加.在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象.不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题.因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义. ...
Equations of anomalous absorption onto swelling porous media
2
2009
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
... 通过上述实验,验证了分形导数模型的可行性,并且可以得到分形导数模型在描述膨胀性土壤反常吸附过程较传统整数阶导数模型的优势,分形导数的拟合精度较高,能够较为全面地表征和预测累积吸附的演化规律,并能够对膨胀性土壤的吸附过程进行分类.需要指出的是,对于文献[19 ] 提出的物质坐标下的分数阶导数模型,采用的是分数阶导数非局部算子,对应的物质坐标是无穷级数的形式.为方便计算,仅采用无穷级数的前两项推导得到了累积吸附的表达式,该累积吸附为时间的幂函数,其中分数阶导数的阶数为1时,退化为正常吸附.该简化方法降低了分数阶导数模型的精度.而物质坐标下的分形导数模型则不存在此问题.本文的工作为地下土体环境污染的治理和修复提供了新的理论参考.后续将结合不同类型的膨胀性土壤水分以及溶质的吸附实验,验证和推广本文的工作. ...
Theory of infiltration: infiltration into swelling soils in a material coordinate
1
2010
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
膨胀性土壤饱和水分运动参数计算模型
1
2018
... 膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土.由于其对环境湿热变化敏感,性质极不稳定.按黏土矿物分类,可以将膨胀土归纳为两大类.一类以蒙脱石为主;另一类以伊利石土和高岭土为主.按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1 ] .土壤膨胀变形受初始含水量[2 ] 以及自重应力[3 ] 的影响,具有明显的非线性流变特征[4 -5 ] ,并且膨胀力和膨胀变形随土壤增湿程度增加而增加.在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象.不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题.因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义. ...
膨胀性土壤饱和水分运动参数计算模型
1
2018
... 膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土.由于其对环境湿热变化敏感,性质极不稳定.按黏土矿物分类,可以将膨胀土归纳为两大类.一类以蒙脱石为主;另一类以伊利石土和高岭土为主.按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1 ] .土壤膨胀变形受初始含水量[2 ] 以及自重应力[3 ] 的影响,具有明显的非线性流变特征[4 -5 ] ,并且膨胀力和膨胀变形随土壤增湿程度增加而增加.在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象.不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题.因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义. ...
南宁膨胀土剪切蠕变特性及流变模型研究
1
2011
... 膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土.由于其对环境湿热变化敏感,性质极不稳定.按黏土矿物分类,可以将膨胀土归纳为两大类.一类以蒙脱石为主;另一类以伊利石土和高岭土为主.按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1 ] .土壤膨胀变形受初始含水量[2 ] 以及自重应力[3 ] 的影响,具有明显的非线性流变特征[4 -5 ] ,并且膨胀力和膨胀变形随土壤增湿程度增加而增加.在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象.不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题.因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义. ...
南宁膨胀土剪切蠕变特性及流变模型研究
1
2011
... 膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土.由于其对环境湿热变化敏感,性质极不稳定.按黏土矿物分类,可以将膨胀土归纳为两大类.一类以蒙脱石为主;另一类以伊利石土和高岭土为主.按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1 ] .土壤膨胀变形受初始含水量[2 ] 以及自重应力[3 ] 的影响,具有明显的非线性流变特征[4 -5 ] ,并且膨胀力和膨胀变形随土壤增湿程度增加而增加.在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象.不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题.因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义. ...
A direct simulation demonstrating the role of special heterogeneity in determining anomalous diffusive transport
1
2015
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
分形多孔介质的粒子扩散特点
1
2004
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
南宁膨胀土非线性流变模型研究
1
2012
... 膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土.由于其对环境湿热变化敏感,性质极不稳定.按黏土矿物分类,可以将膨胀土归纳为两大类.一类以蒙脱石为主;另一类以伊利石土和高岭土为主.按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1 ] .土壤膨胀变形受初始含水量[2 ] 以及自重应力[3 ] 的影响,具有明显的非线性流变特征[4 -5 ] ,并且膨胀力和膨胀变形随土壤增湿程度增加而增加.在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象.不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题.因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义. ...
南宁膨胀土非线性流变模型研究
1
2012
... 膨胀性土壤是含有较多亲水性矿物成分,具有明显的吸水膨胀和失水收缩特性的塑性土.由于其对环境湿热变化敏感,性质极不稳定.按黏土矿物分类,可以将膨胀土归纳为两大类.一类以蒙脱石为主;另一类以伊利石土和高岭土为主.按膨胀性分类可分为弱膨胀、中膨胀、强膨胀三类[1 ] .土壤膨胀变形受初始含水量[2 ] 以及自重应力[3 ] 的影响,具有明显的非线性流变特征[4 -5 ] ,并且膨胀力和膨胀变形随土壤增湿程度增加而增加.在水分渗透吸附的过程中,水分会进入土壤间的孔隙,可侵入黏土的层间,与此同时会逐渐渗透入土体颗粒,引起黏土体积增大的现象.不同污染物在膨胀性土层的扩散过程、含水层在复杂土壤中的渗透过程、垃圾填埋场的选址以及海水倒灌过程均涉及水分在膨胀性土壤中运移规律这一问题.因此研究膨胀性土壤累积吸附过程对工程建设与维护和自然环境保护以及新材料的研发具有重要意义. ...
1
2006
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
Diffusive transport of volatile pollutants in nonaqueous-phase liquid contaminated soil: a fractal model
0
1998
1
2010
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
Connecting complexity with spectral entropy using the Laplace transformed solution to the fractional diffusion equation
1
2016
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
分形多孔介质的粒子扩散特点
1
2004
... 吸附性可以解析地定义为土壤含水量和扩散系数的函数.研究表明,水分在均质、各向同性的环境中,其扩散为菲克扩散[6 -8 ] ,其均方位移为时间的线性函数$\left\langle x^{2} \right\rangle \sim t$,但在膨胀性土壤中的扩散过程较为复杂,不是菲克扩散,而是反常扩散,其均方位移为时间的非线性函数关系$\left\langle x^{2} \right\rangle \sim t^{\alpha }$,当阶数$\alpha >1$时为快扩散,$\alpha<1$时为慢扩散.因此,膨胀性土壤中水分吸附过程偏离正常吸附,为反常吸附过程[9 ] .近年来,分形导数已成功应用于反常输运相关的物理问题上[10 -15 ] ,目前的一些主要工作如下.陈文等[16 ] 采用分形Richards方程推导出更一般的非均质土壤入渗率,并分析了与现有水文模型的关系,其中分形导数的阶数能够刻画土壤的非均质性.曲艺等[17 ] 以Sierpinski分形地毯构建孔隙分形模型模拟多孔介质空间结构,并根据随机行走模型模拟反常扩散过程.王书鸿等[18 ] 利用时空分形导数模型刻画了软物质的磁共振信号衰减的规律,用以表征和区分软物质的内部结构.Su[19 ] 分析了刚性和膨胀性介质中水分渗流的机制,将分数阶导数引入扩散方程中,在物质坐标下给出了累积吸收、吸收速率和反常吸附率的一般方程.随后Su[20 ] 通过考虑重力项的影响,推导了膨胀性多孔介质中水分运动的分数阶Fokker-Planck方程,并给出了方程的基本解.Voller[21 ] 通过渗透实验,构建了不同入渗情况下粒子运动的模型,证明了介质的非均质性与反常扩散之间的相关性.张东辉等[22 ] 采用有限容积法构建了粒子在多孔介质中热传导反常扩散模型.基于现有的工作,本文将采用分形导数建立反常吸附模型,准确刻画膨胀性土壤中水分的吸附过程. ...
The movement of water in swelling materials
2
1968
... 需要指出的是,膨胀土受干湿循环过程的影响,土壤颗粒会不同程度地膨胀或收缩.对于膨胀性土壤,使用经典的固定坐标是不合适的.本文考虑引入物质坐标[15 ] 作为描述膨胀性介质吸附过程的媒介.达西定律描述了流体相对于相对不动的黏土颗粒的流动,该物质坐标理论是基于参考黏土质量分布而定义的长度标度,而不是传统的固定长度标度而发展而来的[23 ] .物质坐标反映固体土壤颗粒的体积与水分的体积之间的关系,通过含水率在垂向的积分体现.物质坐标是含水率和空间位置坐标的函数,通过在垂直方向上积分可以计算出含水率累积吸附量,是描述膨胀土累积吸附的有效工具.因此,本文将基于物质坐标下的分形导数模型,描述膨胀性土壤中水分的累积吸附过程. ...
... 物质坐标不是基于传统的长度标度,而是基于由吸附剂质量分布定义的长度标度,或者当系统内总质量恒定时,根据两个互扩散组分的质量分布而定义的[23 ] .考虑到膨胀土壤的特性,采用物质坐标描述其膨胀性.膨胀性介质的物质坐标定义为[24 ] ...
Mechanics of Swelling
1
1992
... 物质坐标不是基于传统的长度标度,而是基于由吸附剂质量分布定义的长度标度,或者当系统内总质量恒定时,根据两个互扩散组分的质量分布而定义的[23 ] .考虑到膨胀土壤的特性,采用物质坐标描述其膨胀性.膨胀性介质的物质坐标定义为[24 ] ...
The steady-state measurement of the relation between hydraulic conductivity and moisture content in soils
1
1968
... 其中$z$为垂直方向上通常的空间坐标,$e$为孔隙比,$e={\vartheta}/({1-\vartheta})$,$\vartheta ={\vartheta_{{\rm l}}}/{\vartheta_{{\rm s}}}$为含水率,$\vartheta_{{\rm l}}$和$\vartheta_{{\rm s}}$分别为液体和固体的体积分数[25 -26 ] . ...
Hydrology of Swelling Clay Soils. Encyclopedia of Hydrological Sciences
1
2005
... 其中$z$为垂直方向上通常的空间坐标,$e$为孔隙比,$e={\vartheta}/({1-\vartheta})$,$\vartheta ={\vartheta_{{\rm l}}}/{\vartheta_{{\rm s}}}$为含水率,$\vartheta_{{\rm l}}$和$\vartheta_{{\rm s}}$分别为液体和固体的体积分数[25 -26 ] . ...
Infiltration Theory for Hydrologic Applications
1
2002
... 膨胀性土壤中累积吸附的计算表达式[27 -28 ] 为 ...
Recovery of technologically critical lanthanides from ion adsorption soils
1
2021
... 膨胀性土壤中累积吸附的计算表达式[27 -28 ] 为 ...
An experimental study of vertical infiltration into a structurally unstable swelling soil, with particular reference to the infiltration throttle
2
1973
... 该实验中使用的膨胀性土壤为0.5~1.0 mm的黑土表层团聚体对应的累积吸附数据[29 ] .实验中使用了直径为5.09 cm,长为90 cm的有机玻璃柱,其结构类似于土柱.入渗测量采用与土柱相同的方式进行,随着入渗的进行,张力计元件插入湿润锋后面.当柱底出现毛细管条纹并达到稳态流动时,实验终止.由此,在水流达到稳定之前,可以得到入渗水分随着时间的累积吸附曲线. ...
... 对比研究选用膨胀性不明显的砂土累积吸附实验[29 ] .结合水分在砂土中累积吸附的实验数据,用上述类似的方法处理实验数据,拟合得到分形导数模型累积吸附方程中最合适的匹配参数,参数的值为:$\alpha=1.91$,$D_{m}=36.37$ cm$^{2}$/h,均方根误差$e_{1}=0.004 8$.整数阶模型的土壤渗吸率$S=6.80$ cm/h$^{1/2}$,均方根误差$e_{0}=2.174 7$.图3 给出了整数阶以及分形导数模型对应累积吸附量$I-t$的对比曲线.由图3 可知,对于砂土中的水分吸附过程,分形导数模型在时间分形尺度上与传统的整数阶导数模型相比具有较好的拟合效果.并且时间分形导数模型的阶数大于1表明水分在此种砂土中的累积吸附为快吸附,膨胀性不明显. ...