指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] 。在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] 。主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] 。因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] 。国内对指向式导向工具主轴的研究主要包括以下方面。杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析。
目前,国内对指向式导向工具主轴的研究均是将其视为横向弯曲梁,并没有考虑主轴的轴向载荷作用,且未见国内外对指向式导向工具钻压传递机构安装位置进行探讨的文献,但国内外指向式导向工具主轴上却都有钻压传递机构,因此,本文在结合横向弯曲梁和纵横弯曲梁力学模型的基础上,建立了一种考虑轴向载荷的指向式导向工具主轴的力学理论模型,将主轴视为考虑轴向载荷的简支梁,利用有限元[12 -16 ] 法单元划分思想对主轴管柱进行划分[17 ] ,分析钻压传递机构安装位置对指向式导向工具组合偏置力和造斜性能的影响规律,研究结果对优化工具结构和更全面地认识主轴力学行为具有重要意义。
1 指向式导向工具主轴力学模型建立
综合考虑轴向载荷、偏心机构、上支撑轴承、组合轴承等因素的影响,建立指向式旋转导向工具井斜平面主轴的静力学模型,如图1 所示,其中$F$为偏心机构作用在主轴上的等效动位移载荷,并取主轴微元段(图1 中方框标出)进行力学分析。
图1
图1
力学模型简化图
Fig.1
Simplified diagram of mechanical model
图1 中,$M$与$M_{1} $为弯矩,N$\cdot$m;$q$为重力均布载荷,N/m;$P$为轴向载荷,N。在钻头处建立平面坐标系,d$x$是其微元段。取微元段进行力学分析,在$y$轴上建立力的平衡方程可得
(1) $Q-(Q+{\rm d}Q)-q{\rm d}x=0$
其中$Q$为截面剪力,N。 以微元段右侧截面中心为基准,由力矩的平衡方程可得
(2) $Q{\rm d}x-{\rm d}M-P{\rm d}y-\frac{1}{2}q{\rm d}x{\rm d}x=0$
由于$q{\rm d}x{\rm d}x/2$是高阶次的小数,可以忽略。由于[18 -19 ]
(3) $M=-EI\frac{{\rm d}^{2}y}{{\rm d}x^{2}}$
其中$E$是弹性模量,Pa,$I$是惯性矩,m$^{4}$。联立式(1)~式(3)可得
(4) $\frac{{\rm d}^{4}y}{{\rm d}x^{4}}-\frac{P}{EI}\frac{{\rm d}^{2}y}{{\rm d}x^{2}}=\frac{q}{EI}$
当轴向力为压缩力时,$P<0$,令$y=\omega $, 对非齐次线性方程(4)进行求解得
(5) $\begin{array}{c}\omega(x)=C_{1} \sin \left(\sqrt{-\frac{P}{E I}} x\right)+C_{2} \cos \left(\sqrt{-\frac{P}{E I}} x\right)+ \\C_{3} x+C_{4}-\frac{q}{2 P} x^{2}\end{array}$
当主轴没有轴向力作用时,可以视为横向弯曲梁,即$P=0$,令$y=\omega $,对非齐次线性方程(4)进行求解得
(6) $\omega (x)=C_{1} \frac{x^{3}}{6}+C_{2} \frac{x^{2}}{2}+C_{3} x+C_{4}+\frac{q}{24EI}x^{4}$
2 柔性主轴管柱单元组合
2.1 管柱单元几何与力学属性
根据挠度曲线$\omega $,角位移$\theta$,弯矩$M$和剪力$Q$的微分关系,可以得到管柱单元$i$内任意一点$x$处的微分函数[20 ]
(7) $\left[\begin{array}{c}\omega_{i} \\\theta_{i} \\M_{i} \\Q_{i}\end{array}\right]=\left[\begin{array}{c}\omega_{i} \\\omega_{i}^{\prime} \\-E_{i} I_{i} \omega_{i}^{\prime \prime} \\-E_{i} I_{i} \omega_{i}^{\prime \prime \prime}\end{array}\right]$
在纵横弯曲梁段,轴向载荷$P$起压缩作用,即$P<0$,令$k=\sqrt{-{P}/(E_{i}I_{i})}$,则在管柱单元$i$内,任意位置$x$处的挠度、角位移、弯矩和剪力分别为
(8) $\begin{aligned}{\left[\begin{array}{c}\omega_{i}(s) \\\theta_{i}(s) \\M_{i}(s) \\Q_{i}(s)\end{array}\right] } &=\left[\begin{array}{cccc}\sin \left(k_{i} x\right) & \cos \left(k_{i} x\right) & x & 1 \\k_{i} \cos \left(k_{i} x\right) & -k_{i} \sin \left(k_{i} x\right) & 1 & 0 \\E_{i} I_{i}\left[k_{i}^{2} \sin \left(k_{i} x\right)\right. & k_{i}^{2} \cos \left(k_{i} x\right) & 0 & 0 \\E_{i} I_{i}\left[k_{i}^{3} \cos \left(k_{i} x\right)\right. & -k_{i}^{3} \sin \left(k_{i} x\right) & 0 & 0\end{array}\right] \\{\left[\begin{array}{c}C_{i}^{1} \\C_{i}^{2} \\C_{i}^{3} \\C_{i}^{4}\end{array}\right]-\left[\begin{array}{c}\frac{q_{i}}{2 P_{i}} x^{2} \\\frac{q_{i}}{P_{i}} x \\-\frac{E_{i} I_{i} q_{i}}{P_{i}} \\0\end{array}\right] }\end{aligned}$
在横向弯曲梁段,主轴没有受到轴向载荷作用,即$P=0$,则在管柱单元$i$内,任意位置$x$处的挠度、角位移、弯矩和剪力分别为
(9) $\begin{array}{l}{\left[\begin{array}{l}\omega_{i}(s) \\\theta_{i}(s) \\M_{i}(s) \\Q_{i}(s)\end{array}\right]=\left[\begin{array}{cccc}\frac{x^{3}}{6} & \frac{x^{2}}{2} & x & 1 \\\frac{x^{2}}{2} & x & 1 & 0 \\-E_{i} I_{i} x & -E_{i} I_{i} & 0 & 0 \\-E_{i} I_{i} & 0 & 0 & 0\end{array}\right]\left[\begin{array}{c}C_{i}^{1} \\C_{i}^{2} \\C_{i}^{3} \\C_{i}^{4}\end{array}\right]+} \\{\left[\begin{array}{c}\frac{q_{i} x^{4}}{24 E_{i} I_{i}} \\\frac{q_{i} x^{3}}{6 E_{i} I_{i}} \\-\frac{q_{i} x^{2}}{2} \\-q_{i} x\end{array}\right]}\end{array}$
2.2 单元节点连接条件
通过对主轴划分得到的管柱单元,实质上是通过节点属性值,按照管柱的连续性质和约束性质串联组合在一起,如图2 所示。按照节点连接的性质,整个管柱单元系统的节点可分为边界节点和相邻节点,按照节点处的约束性质、连续性,可以得到每个单元在节点处的组合关系,具体如下所示。
(10) $\left.\begin{array}{l} \omega_{i} (x\vert_{x=0\mbox{\scriptsize或}x=L_{i}})=e_{\omega_{i-1} } \\ M_{i} (x\vert_{x=0\mbox{\scriptsize或}x=L_{i}})=0 \\ \end{array} \right\}$
图2
图2
主轴单元节点属性图铰支节点
Fig.2
Spindle element node attribute diagram
(11) $\left. {\begin{array}{l} \omega_{i} (x\vert_{x=L_{i} } )-\omega_{i+1} (x\vert_{x=0} )=0 \\ \theta_{i} (x\vert_{x=L_{i} } )-\theta_{i+1} (x\vert_{x=0} )=0 \\ M_{i} (x\vert_{x=L_{i} } )-M_{i+1} (x\vert_{x=0} )=0 \\ Q_{i} (x\vert_{x=L_{i} } )-Q_{i+1} (x\vert_{x=0} )=0 \\ \end{array}} \right\}$
(12) $\left. {\begin{array}{l} \omega_{i} (x\vert_{x=L_{i} } )-\omega_{i+1} (x\vert_{x=0} )=0 \\ \theta_{i} (x\vert_{x=L_{i} } )-\theta_{i+1} (x\vert_{x=0} )=0 \\ M_{i} (x\vert_{x=L_{i} } )-M_{i+1} (x\vert_{x=0} )=0 \\ \omega_{i+1} (x\vert_{x=0} )=e_{\omega_{i} } \\ \end{array}} \right\}$
(13) $\left. {\begin{array}{l} \omega_{i} (x\vert_{x=0\mbox{\scriptsize或}x=L_{i}})=e_{\omega_{i-1} } \\ \theta_{i} (x\vert_{x=0\mbox{\scriptsize或}x=L_{i}})=0 \\ \end{array}} \right\}$
其中$e_{\omega_{i-1}}$为该节点处的初始横向位移。
3 主轴偏置力与造斜能力分析
指向式导向钻井工具在定向钻井的过程中,导向轴是在偏置的状态下旋转带动钻头进行造斜[21 ] ,在偏心机构偏置力作用点处主轴的受力最为恶劣,且钻头倾角和钻头侧向力与导向工具造斜率成正相关关系[9 ] 。因此,在主轴力学模型中需要分析钻压传递机构安装位置对主轴偏置力、钻头侧向力与钻头倾角的影响规律。
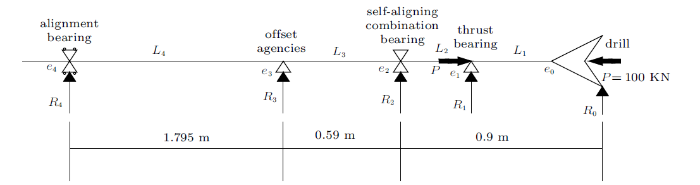
利用单元划分的思想,以主轴上的零部件为节点将主轴分为四个单元,如图3 所示,钻头为铰支节点、止推轴承为悬空节点、调心组合轴承和偏置机构为支座节点、扶正轴承为固定节点。指向式导向工具中止推轴承作为钻压传递机构时,可以将地层对钻头的钻压反力传递给外壳,避免主轴控制段承受轴向载荷,其在钻头到调心组合轴承之间移动。按照主轴是否承受轴向力可以分为纵横弯曲段和横向弯曲段,因此,钻头至止推轴承段管柱单元为纵横弯曲段,剩下的管柱单元皆为横向弯曲段。
图3
图3
工具主轴结构参数图
Fig.3
Tool spindle structure parameter drawing
令钻压传递机构安装相对位置为$L_1/(L_1+L_2)=a$,$0\leqslant a\leqslant 1$,$a=0$时止推轴承放在钻头处,$a=1$时止推轴承放在调心组合轴承处。则由式(5)~式(9)可知钻头倾角
(14) $\theta_{0} =C_{1}^{1} \cdot k+C_{1}^{3}$
(15) $R_{0} =E_{1} I_{1} k_{1} C_{1}^{1}$
(16) $R_{3} =E_{4} I_{4} C_{4}^{1} -E_{3} I_{3} C_{3}^{1} -qL_{3}$
工具主轴材料[10 ] 为42CrMo,主轴弹性模量$E$=195 GPa,泊松比为0.3,主轴外径为70 mm,内径为40 mm,截面极惯性矩$I=1.052 9 \times 10^{-6} m^{4}$,密度$\rho=7.8 t/m^{3}$,线性重量$q=20.216$ kg,偏置量$e_{c}=6$ mm。主轴划分为4个单元,力学方程组共有16个未知数,以$C_{i}^{1}$,$C_{i}^{2}$,$C_{i}^{3}$,$C_{i}^{4}$表示,i=1,2,3,4。利用式(5)~式(9)与节点连接条件联合建立未知数矩阵方程(17),便于MATLAB编程求解未知数所用[21 ] 。
(17)
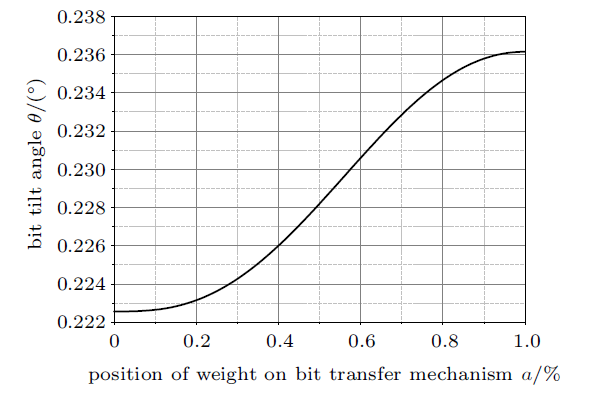
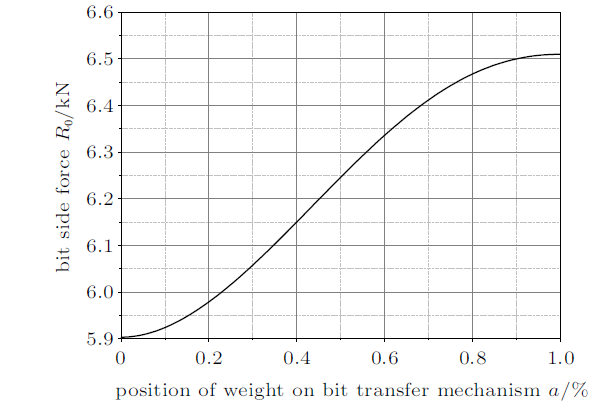
通过对该矩阵进行求解并结合式(14)~式(16),得到在主轴长度保持一定且偏置机构偏置量保持最大6 mm不变的情况下,钻头倾角$\theta_{0} $,钻头侧向力$R_{0} $,偏置力$R_{3}$随着止推轴承安装位置在钻头至调心组合轴承之间变化而变化的规律,见图4 ~图6 。
图4
图4
钻头倾角随止推轴承位置变化图
Fig.4
Diagram of bit inclination changing with thrust bearing position
图5
图5
钻头侧向力随止推轴承位置变化图
Fig.5
Diagram of bit lateral force changing with thrust bearing position
图6
图6
偏置力随止推轴承位置变化图
Fig.6
Diagram of offset force changing with thrust bearing position
由图4 可看出,随着止推轴承安装位置距离调心组合轴承越近,钻头倾角总体呈上升趋势,且在钻头和调心组合轴承处上升趋势较缓,而在两者之间钻头倾角上升趋势较为显著,止推轴承安装位置在钻头处与在调心组合轴承处相比,钻头倾角相差可达到0.013$^\circ$。
由图5 可看出,钻头侧向力随着止推轴承安装位置距离调心组合轴承越近而越大,且变化趋势与钻头倾角变化趋势相似。在钻头和调心组合轴承处,钻头侧向力变化较小,而在两者之间变化较为明显,止推轴承安装位置在钻头处与在调心组合轴承处相比,钻头侧向力相差可达到610 N。
由图6 可看出,随着止推轴承安装位置越靠近调心组合轴承,偏置机构偏置力呈下降趋势,且在钻头和调心组合轴承处下降趋势较缓,而在两者之间下降趋势较为明显,止推轴承安装位置在钻头处与在调心组合轴承处相比,偏置力相差可达到369 N。
在旋转导向系统中,主轴的径向刚度以主轴的偏置力与主轴产生最大挠度的比值来定义[22 ] ,即主轴刚度
(18) $K=\frac{R_{3} }{y_{\max } }$
止推轴承安装位置变化对主轴径向刚度的影响规律见图7 ,随着钻压传递机构安装位置距离组合轴承越近,主轴刚度呈现下降趋势,但影响较小,最大值与最小值之差仅为46 N/mm,可忽略不计。
图7
图7
主轴刚度随止推轴承位置变化图
Fig.7
Diagram of spindle rigidity changing with thrust bearing position
因此,为保证旋转导向系统的造斜率尽可能大并且使主轴的承载尽可能小,从而延长主轴的使用寿命,在考虑导向工具的结构安排及受力后,钻压传递机构安装位置应尽量靠近调心组合轴承。
4 结论
(1) 在结合横向弯曲梁和纵横弯曲梁力学模型的基础上,建立了一种考虑轴向载荷的指向式导向钻具组合的力学理论模型,对工具主轴进行力学分析,得到平面管柱力学微分方程,进而推导出主轴管柱各单元挠度、转角、弯矩及剪力的计算公式。
(2) 分析了钻压传递机构在主轴上的安装相对位置对偏置力的影响规律,得出结论,在主轴长度和偏心机构偏置量一定的情况下,随着钻压传递机构安装位置靠近调心组合轴承,主轴造斜所需的偏置力将减小,由23.897 kN减小至23.528 kN。
(3) 分析了钻压传递机构在主轴上的安装相对位置对主轴造斜性能的影响规律,随着钻压传递机构安装位置靠近调心组合轴承,导向工具的钻头侧向力与钻头倾角将增大,钻头倾角由0.223$^\circ$增大至0.236$^\circ$,钻头侧向力由5.9 kN增大至6.51 kN。
(4) 分析了钻压传递机构在主轴上的安装相对位置对主轴刚度的影响规律,得出结论,随着钻压传递机构安装位置靠近调心组合轴承,主轴刚度将减小,由3.37 kN/mm减小至3.33 kN/mm,钻压传递机构安装位置的变化对主轴的刚度影响较弱。
参考文献
View Option
[1]
冯定 , 王鹏 , 张红 等 . 旋转导向工具研究现状及发展趋势
石油机械 , 2021 , 49 (7 ):8 -15
[本文引用: 1]
Feng Ding Wang Peng Zhang Hong , et al . Research status and development trend of rotary steerable system tool
China Petroleum Machinery 2021 , 49 (7 ):8 -15 (in Chinese)
[本文引用: 1]
[2]
冯定 , 卢昌 , 张红 等 . 井眼轨迹控制工具导向运动控制研究
石油矿场机械 , 2017 , 46 (1 ):6 -10
[本文引用: 1]
Feng Ding Lu Chang Zhang Hong , et al . Research on control of steering movement of well trajectory control tool
Oil Field Equipment 2017 , 46 (1 ):6 -10 (in Chinese)
[本文引用: 1]
[3]
张光伟 , 乔阳 , 田帆 等 . 全旋转内置式导向钻井工具动力学分析及仿真
机械强度 , 2020 , 42 (6 ):1417 -1423
[本文引用: 2]
Zhang Guangwei Qiao Yang Tian fan , et al . Dynamic analysis and simulation of full rotary built-in steering drilling tools
Journal of Mechanical Strength 2020 , 42 (6 ):1417 -1423 (in Chinese)
[本文引用: 2]
[4]
杜建生 , 刘宝林 , 李清涛 等 . 指向式旋转导向系统偏置心轴力学模型及优化
石油机械 , 2008 , 36 (8 ):28 -35
[本文引用: 1]
Du Jiansheng Liu Baolin Li Qingtao , et al . The mechanical model establishment and optimization of the rotary shaft in the point-the-bit rotary steerable drilling system
China Petroleum Machinery 2008 , 36 (8 ):28 -35 (in Chinese)
[本文引用: 1]
[5]
刘江民 . 复合式旋转导向钻井工具造斜能力分析与设计. [硕士论文]
西安: 西安石油大学 , 2018
[本文引用: 1]
Liu Jiangmin . Analysis and design of build-up capacity of compound rotary steerable drilling tool. [Master Thesis]
Xi'an: Xi'an Petroleum University 2018 (in Chinese)
[本文引用: 1]
[6]
杨磊 . 指向式旋转导向钻井工具动力学分析. [硕士论文]
大庆: 东北石油大学 , 2017
[本文引用: 1]
Yang Lei . Dynamic analysis of directional rotary steering drilling tool. [Master Thesis]
Daqing: Northeast Petroleum University 2017 (in Chinese)
[本文引用: 1]
[7]
冯定 , 鄢标 , 夏成宇 等 . 井眼轨迹控制工具主轴力学行为分析
科学技术与工程 , 2016 , 16 (4 ):173 -177
[本文引用: 1]
Feng Ding Yan Biao Xia Chengyu , et al . The mechanical behavior analysis of spindle in wellbore track control tool
Science Technology & Engineering 2016 , 16 (4 ):173 -177 (in Chinese)
[本文引用: 1]
[8]
冯定 , 肖苏宸 , 夏成宇 . 高造斜井眼轨迹控制工具主轴力学分析与试验研究
石油机械 , 2014 , 42 (10 ):34 -36
[本文引用: 1]
Feng Ding Xiao Suchen Xia Chengyu . Mechanical analysis and experimental study of tool spindle for trajectory control of high deviation hole
China Petroleum Machinery 2014 , 42 (10 ):34 -36 (in Chinese)
[本文引用: 1]
[9]
Feng D Wu L Wang JW , et al . Research on eccentric displacement of the trajectory control tool of high build-uprate wellbore
2012 International Conference on Future Electrical Power and Energy Systems, Sanya, China , 2012
[本文引用: 2]
[10]
张红 . 基于井眼轨迹控制工具的主轴造斜性能研究. [博士论文]
荆州: 长江大学 , 2017
[本文引用: 2]
Zhang Hong . Research on deflection performance of spindle based on borehole trajectory control tool. [PhD Thesis]
Jingzhou: Yangtze University 2017 (in Chinese)
[本文引用: 2]
[11]
张红 , 向正新 , 钱利勤 等 . 井眼轨迹控制工具主轴载荷与造斜能力关系研究
力学与实践 , 2017 , 39 (2 ):152 -157, 134
[本文引用: 1]
Zhang Hong Xiang Zhengxin Qian Liqin , et al . Study on the relationship between spindle load and deflection ability of borehole trajectory control tool
Mechanics in Engineering 2017 , 39 (2 ):152 -157, 134 (in Chinese)
DOI
URL
[本文引用: 1]
[12]
Millheim K Jordan S Ritter CJ . Bottom-hole assembly analysis using the finite-element method
Journal of petroleum technology 1978 , 30 (2 ):265 -274
DOI
URL
[本文引用: 1]
[13]
Khulief YA Al-Naser H . Finite element dynamic analysis of drill strings
Finite Element in Analysis and Design 2005 , 41 (13 ):1270 -1288
DOI
URL
[14]
Zhang X Xu X Wang L . Finite element analysis for buckling behaviour of coiled tubing in horizontal wellbores
International Journal of Computer Applications in Technology 2012 , 45 (4 ):266
DOI
URL
[15]
Mcspadden AR Coker OD Ruan GC . Advanced casing design with finite-element model of effective dogleg severity, radial displacements, and bending loads
SPE Drilling & Completion 2012 , 27 (3 ):436 -448
[16]
Zhu XZ He YD Chen L , et al . Nonlinear dynamics analysis of a drillstring-bit-wellbore system for horizontal oil well
Advanced Science Letters 2012 , 16 (1 ):13 -19
DOI
URL
[本文引用: 1]
[17]
洪迪峰 , 唐雪平 , 苏义脑 等 . 非连续性旋转导向钻具组合的广义纵横弯曲法
石油学报 , 2014 , 35 (3 ):543 -550
[本文引用: 1]
Hong Difeng Tang Xueping Su Yinao , et al . Generalized beam-column method for non-continuous rotary steering drilling of bottom-hole assembly
Acta Petrolei Sinica 2014 , 35 (3 ):543 -550 (in Chinese)
[本文引用: 1]
[18]
李敏 , 李依伦 . 材料力学中小变形假设辨析
力学与实践 , 2021 , 43 (3 ):420 -424
[本文引用: 1]
Li Min Li Yilun . Discussion of small deformation hypothesis in mechanics of materials
Mechanics in Engineering 2021 , 43 (3 ):420 -424 (in Chinese)
[本文引用: 1]
[19]
张劲夫 . 两端固定的等截面梁在均布载荷作用下的挠曲线
力学与实践 , 2018 , 40 (1 ):96 -97
[本文引用: 1]
Zhang Jingfu . The deflection line of a beam of uniform section fixed at both ends under uniform load
Mechanics in Engineering 2018 , 40 (1 ):96 -97 (in Chinese)
[本文引用: 1]
[20]
韩涛 , 练章华 , 丁亮亮 . 深水无隔水管钻井套管下入力学影响因素分析
重庆科技学院学报(自然科学版) , 2011 , 13 (5 ):66 -68
[本文引用: 1]
Han Tao Lian Zhanghua Ding Liangliang . The analysis of mechanical factors of casing down into the well in deep-water, riser-less drilling
Journal of Chongqing University of Science and Technology $($Natural Sciences Edition$)$ 2011 , 13 (5 ):66 -68 (in Chinese)
[本文引用: 1]
[21]
孙学珍 . 带旋转导向钻井工具的下部钻具组合力学分析. [硕士论文]
西安: 西安石油大学 , 2018
[本文引用: 2]
Sun Xuezhen . Mechanical analysis of bottomhole assembly with rotary steerable drilling tool. [Master Thesis]
Xi'an: Xi'an Shiyou University 2018 (in Chinese)
[本文引用: 2]
[22]
高英贤 , 刘洋 , 张允良 . 数控机床轴承预紧对主轴刚度的影响
组合机床与自动化加工技术 , 2013 (7 ):31 -33
[本文引用: 1]
Gao Yingxian Liu Yang Zhang Yunliang . Influence of bearing preload on spindle stiffness of CNC machine tool
Modular Machine Tool & Automatic Manufacturing Technique 2013 (7 ):31 -33 (in Chinese)
[本文引用: 1]
旋转导向工具研究现状及发展趋势
1
2021
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
旋转导向工具研究现状及发展趋势
1
2021
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
井眼轨迹控制工具导向运动控制研究
1
2017
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
井眼轨迹控制工具导向运动控制研究
1
2017
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
全旋转内置式导向钻井工具动力学分析及仿真
2
2020
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
... [3 ]建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
全旋转内置式导向钻井工具动力学分析及仿真
2
2020
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
... [3 ]建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
指向式旋转导向系统偏置心轴力学模型及优化
1
2008
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
指向式旋转导向系统偏置心轴力学模型及优化
1
2008
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
复合式旋转导向钻井工具造斜能力分析与设计. [硕士论文]
1
2018
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
复合式旋转导向钻井工具造斜能力分析与设计. [硕士论文]
1
2018
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
指向式旋转导向钻井工具动力学分析. [硕士论文]
1
2017
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
指向式旋转导向钻井工具动力学分析. [硕士论文]
1
2017
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
井眼轨迹控制工具主轴力学行为分析
1
2016
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
井眼轨迹控制工具主轴力学行为分析
1
2016
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
高造斜井眼轨迹控制工具主轴力学分析与试验研究
1
2014
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
高造斜井眼轨迹控制工具主轴力学分析与试验研究
1
2014
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
Research on eccentric displacement of the trajectory control tool of high build-uprate wellbore
2
2012
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
... 指向式导向钻井工具在定向钻井的过程中,导向轴是在偏置的状态下旋转带动钻头进行造斜[21 ] ,在偏心机构偏置力作用点处主轴的受力最为恶劣,且钻头倾角和钻头侧向力与导向工具造斜率成正相关关系[9 ] .因此,在主轴力学模型中需要分析钻压传递机构安装位置对主轴偏置力、钻头侧向力与钻头倾角的影响规律. ...
基于井眼轨迹控制工具的主轴造斜性能研究. [博士论文]
2
2017
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
... 工具主轴材料[10 ] 为42CrMo,主轴弹性模量$E$=195 GPa,泊松比为0.3,主轴外径为70 mm,内径为40 mm,截面极惯性矩$I=1.052 9 \times 10^{-6} m^{4}$,密度$\rho=7.8 t/m^{3}$,线性重量$q=20.216$ kg,偏置量$e_{c}=6$ mm.主轴划分为4个单元,力学方程组共有16个未知数,以$C_{i}^{1}$,$C_{i}^{2}$,$C_{i}^{3}$,$C_{i}^{4}$表示,i=1,2,3,4.利用式(5)~式(9)与节点连接条件联合建立未知数矩阵方程(17),便于MATLAB编程求解未知数所用[21 ] . ...
基于井眼轨迹控制工具的主轴造斜性能研究. [博士论文]
2
2017
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
... 工具主轴材料[10 ] 为42CrMo,主轴弹性模量$E$=195 GPa,泊松比为0.3,主轴外径为70 mm,内径为40 mm,截面极惯性矩$I=1.052 9 \times 10^{-6} m^{4}$,密度$\rho=7.8 t/m^{3}$,线性重量$q=20.216$ kg,偏置量$e_{c}=6$ mm.主轴划分为4个单元,力学方程组共有16个未知数,以$C_{i}^{1}$,$C_{i}^{2}$,$C_{i}^{3}$,$C_{i}^{4}$表示,i=1,2,3,4.利用式(5)~式(9)与节点连接条件联合建立未知数矩阵方程(17),便于MATLAB编程求解未知数所用[21 ] . ...
井眼轨迹控制工具主轴载荷与造斜能力关系研究
1
2017
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
井眼轨迹控制工具主轴载荷与造斜能力关系研究
1
2017
... 指向式旋转导向工具是目前最为先进的定向钻井工具,其钻出的井眼质量较好,适应目前油藏开发的发展趋势[1 -2 ] .在导向工具钻井作业时,主轴是实现导向钻进的关键部件[3 ] .主轴在偏置状态下控制导向工具的造斜率,受到弯扭矩组合交变应力的影响,若直接通过主轴来传递钻压,将会使其受力情况更为恶劣,工作寿命大幅缩减[4 ] .因此,在考虑工程设计可行性的基础上,在上支撑轴承处钻压将通过钻压传递机构传递到外壳上,绕过主轴的控制段(上支撑轴承处到下支撑轴承处),然后在下支撑轴承处通过钻压传递机构传递给钻头,以此来确使主轴在偏置状态下只承受偏置力造成的弯扭组合应力,而不承受钻压,进而提高了主轴的工作寿命[5 ] .国内对指向式导向工具主轴的研究主要包括以下方面.杨磊[6 ] 建立了指向式导向工具芯轴的力学模型,推导出主轴控制段的几何方程,并对偏置力作用点位置进行了优化分析;冯定等[7 -8 ] 和Feng等[9 ] 建立了井眼轨迹控制工具主轴的力学模型,推导出钻头倾角和主轴变形轨迹的计算公式,分析了主轴转速、偏置量及钻压对主轴力学行为的影响;张红等[10 -11 ] 建立了井眼轨迹控制工具主轴的静力学模型,得到主轴的挠度和偏转角的计算公式和偏置力关于外壳、主轴、偏心机构、钻压等参数的表达式;张光伟等[3 ] 建立了导向轴的力学模型,对其所受的偏置力、钻头侧向力和轴向力进行了分析. ...
Bottom-hole assembly analysis using the finite-element method
1
1978
... 目前,国内对指向式导向工具主轴的研究均是将其视为横向弯曲梁,并没有考虑主轴的轴向载荷作用,且未见国内外对指向式导向工具钻压传递机构安装位置进行探讨的文献,但国内外指向式导向工具主轴上却都有钻压传递机构,因此,本文在结合横向弯曲梁和纵横弯曲梁力学模型的基础上,建立了一种考虑轴向载荷的指向式导向工具主轴的力学理论模型,将主轴视为考虑轴向载荷的简支梁,利用有限元[12 -16 ] 法单元划分思想对主轴管柱进行划分[17 ] ,分析钻压传递机构安装位置对指向式导向工具组合偏置力和造斜性能的影响规律,研究结果对优化工具结构和更全面地认识主轴力学行为具有重要意义. ...
Finite element dynamic analysis of drill strings
0
2005
Finite element analysis for buckling behaviour of coiled tubing in horizontal wellbores
0
2012
Advanced casing design with finite-element model of effective dogleg severity, radial displacements, and bending loads
0
2012
Nonlinear dynamics analysis of a drillstring-bit-wellbore system for horizontal oil well
1
2012
... 目前,国内对指向式导向工具主轴的研究均是将其视为横向弯曲梁,并没有考虑主轴的轴向载荷作用,且未见国内外对指向式导向工具钻压传递机构安装位置进行探讨的文献,但国内外指向式导向工具主轴上却都有钻压传递机构,因此,本文在结合横向弯曲梁和纵横弯曲梁力学模型的基础上,建立了一种考虑轴向载荷的指向式导向工具主轴的力学理论模型,将主轴视为考虑轴向载荷的简支梁,利用有限元[12 -16 ] 法单元划分思想对主轴管柱进行划分[17 ] ,分析钻压传递机构安装位置对指向式导向工具组合偏置力和造斜性能的影响规律,研究结果对优化工具结构和更全面地认识主轴力学行为具有重要意义. ...
非连续性旋转导向钻具组合的广义纵横弯曲法
1
2014
... 目前,国内对指向式导向工具主轴的研究均是将其视为横向弯曲梁,并没有考虑主轴的轴向载荷作用,且未见国内外对指向式导向工具钻压传递机构安装位置进行探讨的文献,但国内外指向式导向工具主轴上却都有钻压传递机构,因此,本文在结合横向弯曲梁和纵横弯曲梁力学模型的基础上,建立了一种考虑轴向载荷的指向式导向工具主轴的力学理论模型,将主轴视为考虑轴向载荷的简支梁,利用有限元[12 -16 ] 法单元划分思想对主轴管柱进行划分[17 ] ,分析钻压传递机构安装位置对指向式导向工具组合偏置力和造斜性能的影响规律,研究结果对优化工具结构和更全面地认识主轴力学行为具有重要意义. ...
非连续性旋转导向钻具组合的广义纵横弯曲法
1
2014
... 目前,国内对指向式导向工具主轴的研究均是将其视为横向弯曲梁,并没有考虑主轴的轴向载荷作用,且未见国内外对指向式导向工具钻压传递机构安装位置进行探讨的文献,但国内外指向式导向工具主轴上却都有钻压传递机构,因此,本文在结合横向弯曲梁和纵横弯曲梁力学模型的基础上,建立了一种考虑轴向载荷的指向式导向工具主轴的力学理论模型,将主轴视为考虑轴向载荷的简支梁,利用有限元[12 -16 ] 法单元划分思想对主轴管柱进行划分[17 ] ,分析钻压传递机构安装位置对指向式导向工具组合偏置力和造斜性能的影响规律,研究结果对优化工具结构和更全面地认识主轴力学行为具有重要意义. ...
材料力学中小变形假设辨析
1
2021
... 由于$q{\rm d}x{\rm d}x/2$是高阶次的小数,可以忽略.由于[18 -19 ] ...
材料力学中小变形假设辨析
1
2021
... 由于$q{\rm d}x{\rm d}x/2$是高阶次的小数,可以忽略.由于[18 -19 ] ...
两端固定的等截面梁在均布载荷作用下的挠曲线
1
2018
... 由于$q{\rm d}x{\rm d}x/2$是高阶次的小数,可以忽略.由于[18 -19 ] ...
两端固定的等截面梁在均布载荷作用下的挠曲线
1
2018
... 由于$q{\rm d}x{\rm d}x/2$是高阶次的小数,可以忽略.由于[18 -19 ] ...
深水无隔水管钻井套管下入力学影响因素分析
1
2011
... 根据挠度曲线$\omega $,角位移$\theta$,弯矩$M$和剪力$Q$的微分关系,可以得到管柱单元$i$内任意一点$x$处的微分函数[20 ] ...
深水无隔水管钻井套管下入力学影响因素分析
1
2011
... 根据挠度曲线$\omega $,角位移$\theta$,弯矩$M$和剪力$Q$的微分关系,可以得到管柱单元$i$内任意一点$x$处的微分函数[20 ] ...
带旋转导向钻井工具的下部钻具组合力学分析. [硕士论文]
2
2018
... 指向式导向钻井工具在定向钻井的过程中,导向轴是在偏置的状态下旋转带动钻头进行造斜[21 ] ,在偏心机构偏置力作用点处主轴的受力最为恶劣,且钻头倾角和钻头侧向力与导向工具造斜率成正相关关系[9 ] .因此,在主轴力学模型中需要分析钻压传递机构安装位置对主轴偏置力、钻头侧向力与钻头倾角的影响规律. ...
... 工具主轴材料[10 ] 为42CrMo,主轴弹性模量$E$=195 GPa,泊松比为0.3,主轴外径为70 mm,内径为40 mm,截面极惯性矩$I=1.052 9 \times 10^{-6} m^{4}$,密度$\rho=7.8 t/m^{3}$,线性重量$q=20.216$ kg,偏置量$e_{c}=6$ mm.主轴划分为4个单元,力学方程组共有16个未知数,以$C_{i}^{1}$,$C_{i}^{2}$,$C_{i}^{3}$,$C_{i}^{4}$表示,i=1,2,3,4.利用式(5)~式(9)与节点连接条件联合建立未知数矩阵方程(17),便于MATLAB编程求解未知数所用[21 ] . ...
带旋转导向钻井工具的下部钻具组合力学分析. [硕士论文]
2
2018
... 指向式导向钻井工具在定向钻井的过程中,导向轴是在偏置的状态下旋转带动钻头进行造斜[21 ] ,在偏心机构偏置力作用点处主轴的受力最为恶劣,且钻头倾角和钻头侧向力与导向工具造斜率成正相关关系[9 ] .因此,在主轴力学模型中需要分析钻压传递机构安装位置对主轴偏置力、钻头侧向力与钻头倾角的影响规律. ...
... 工具主轴材料[10 ] 为42CrMo,主轴弹性模量$E$=195 GPa,泊松比为0.3,主轴外径为70 mm,内径为40 mm,截面极惯性矩$I=1.052 9 \times 10^{-6} m^{4}$,密度$\rho=7.8 t/m^{3}$,线性重量$q=20.216$ kg,偏置量$e_{c}=6$ mm.主轴划分为4个单元,力学方程组共有16个未知数,以$C_{i}^{1}$,$C_{i}^{2}$,$C_{i}^{3}$,$C_{i}^{4}$表示,i=1,2,3,4.利用式(5)~式(9)与节点连接条件联合建立未知数矩阵方程(17),便于MATLAB编程求解未知数所用[21 ] . ...
数控机床轴承预紧对主轴刚度的影响
1
2013
... 在旋转导向系统中,主轴的径向刚度以主轴的偏置力与主轴产生最大挠度的比值来定义[22 ] ,即主轴刚度 ...
数控机床轴承预紧对主轴刚度的影响
1
2013
... 在旋转导向系统中,主轴的径向刚度以主轴的偏置力与主轴产生最大挠度的比值来定义[22 ] ,即主轴刚度 ...