热力耦合作用下碳质千枚岩强度演化规律分析

doi:10.6052/1000-0879-21-331

热力耦合作用下碳质千枚岩强度演化规律分析

杨丙昌^,¹⁾

中铁十四局集团第五工程有限公司,山东兖州 272100

STRENGTH EVOLUTION OF CARBONACEOUS PHYLLITE UNDER THERMAL MECHANICAL COUPLING

YANG Bingchang^,¹⁾

The Fivth Project Company Limited of China Railway Bureau 14 Group, Yanzhou 272100, Shandong, China

通讯作者: 1)杨丙昌,高级工程师,研究方向为岩石力学基本特性和地下工程的建设及管理。E-mail:984602578@qq.com

责任编辑: 胡漫王永会

收稿日期: 2021-08-5 修回日期: 2021-08-22

Received: 2021-08-5 Revised: 2021-08-22

作者简介 About authors

摘要

温度场与应力场是影响碳质千枚岩地层引水隧洞围岩强度的重要因素。设定2因素4水平16组试验,依据单轴与三轴试验结果,探讨热力耦合作用下碳质千枚岩应力-应变曲线性态与破坏模式,得到了峰值强度变化规律;基于Mohr-Coulomb强度准则(M-C)与Heok-Brown强度准则(H-B),分别建立了热力耦合作用下Mohr-Coulomb-Thermal法(M-C-T)和Heok-Brown-Thermal法(H-B-T)两种破坏强度计算方法。试验结果与理论分析表明,随围压增大与温度升高,碳质千枚岩从脆性破坏逐渐转为延性破坏,黏聚力、单轴抗压强度和参数$n$随温度升高呈线性增大,内摩擦角受温度影响不显著。通过试验值与计算对比分析,M-C-T法和H-B-T法均能较好地量化热力耦合作用下碳质千枚岩强度演化规律;误差分析表明,前者计算误差为$-$28.5%~7.7%,后者为$-$8.9%~5.6%,H-B-T法计算结果离散程度较小,稳定性更高,且更偏向于安全。

关键词： 热力耦合; 碳质千枚岩; 强度演化; 应力-应变

Abstract

Temperature field and stress field are important factors that affect the surrounding rock strength of diversion tunnel in carbonaceous phyllite stratum. 16 groups of experiments with 2 factors and 4 levels were set. Based on the results of uniaxial and triaxial tests, the behavior of stress-strain curve and the failure mode of carbonaceous phyllite under thermal mechanical coupling are discussed, and the variation law of peak strength is obtained. Based on Mohr-Coulomb (M-C) criterion and Heok-Brown (H-B) criterion, two calculation methods of failure strength, Mohr-Coulomb-Thermal (M-C-T) method and Heok-Brown-Thermal (H-B-T) method, are established respectively. The experimental results and theoretical analysis show that with the increase of confining pressure and temperature, the failure of carbonaceous phyllite changes from brittle to ductile. The cohesion, uniaxial compressive strength and parameter $n$ increase linearly with the increase of temperature, but the internal friction angle is not affected remarkably by temperature. The results show that both M-C-T method and H-B-T method can quantify the strength evolution of carbonaceous phyllite under thermal mechanical coupling. Error analysis shows that the calculation error of the former is $-$28.5%~7.7%, and that of the latter is $-$8.9%~5.6%. The results of H-B-T method show less scattering, hence the method is more stable and more safety oriented.

Keywords： thermal mechanical coupling; carbonaceous phyllite; strength evolution; stress-strain

PDF (324KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨丙昌. 热力耦合作用下碳质千枚岩强度演化规律分析. 力学与实践, 2022, 44(2): 303-309 DOI:10.6052/1000-0879-21-331

YANG Bingchang. STRENGTH EVOLUTION OF CARBONACEOUS PHYLLITE UNDER THERMAL MECHANICAL COUPLING. Mechanics in Engineering, 2022, 44(2): 303-309 DOI:10.6052/1000-0879-21-331

地温(热)与地应力(力)是影响变质岩区域深埋软岩隧洞掘进过程与安全管理的重要因素。西南山区条件复杂多变,地层岩性受地质构造控制,川藏铁路、南水北调西线及各类水利枢纽等基础工程在修建过程中常需穿越高地温的深埋变质岩体区域^[1],如新疆公格尔水电站引水洞石墨片岩地温维持50℃~70℃,云南贡嘎隧道千枚岩地温达45℃,黑白水电站引水洞页岩地温达57℃等。四川毛尔盖水电站引水洞地处高地温大埋深的碳质千枚岩地层,隧洞开挖诱发了围岩应力重分布,加之因掘进作业降温的温差效应,加剧了断面收缩、衬砌开裂及顶板坍塌等大变形灾害发生频度,影响了掘进过程岩体受力特性评判、围岩稳定性评价与施工安全管理,亟待查明热力耦合作用下碳质千枚岩强度演化规律。

热力作用下围岩体强度演化规律成为了岩石工程中备受关注的研究方向之一。李天斌等^[2]通过模型试验发现了地温变化诱发了围岩附加温度应力,增大了其脆性破坏概率;陈子全等^[3]从能量耗散角度得出了碳质千枚岩强度与塑性随围压增加而增强,其破坏形式从压致拉裂转为剪切滑移;孟召平等^[4]采用单因素分析法用影响系数分别量化温度场与应力场对砂岩强度影响。孟陆波等^[5]定性指出了应力场是软岩隧洞大变形的主要因素,温度场对围岩强度存在初始热损伤作用;朱珍德等^[6]建立了大理岩热力耦合作用下细微观模型,指出温度变化下热应力引起了细观裂纹发育,强度随温度升高而降低;严健等^[7]指出热力耦合作用下隧道通风降低了岩体温度,同时诱导了围岩板裂化结构面,呈剪切断裂型破坏形式。朱振南等^[8]引入正态分布,采用Mohr-Coulomb强度准则(M-C准则)量化温度场对岩石统计热损伤效应,高玮等^[9]依据Weibull分布和Heok-Brown强度准则(H-B准则)探讨了不同围压下破裂岩体强度特性。Drucker-Prager准则、非线性M-C准则、Bieniawski幂函数准则、指数强度准则等强度理论及其改进形式也用于描述多因素作用下岩体强度变化规律^[10-11];其中,依据大量试验数据所建立的M-C准则与H-B准则仍为工程设计与施工人员所广泛使用的强度理论。

隧道围岩体强度演化是多种因素共同影响的体现,当前对热力耦合作用下软岩的强度变化规律的研究还较少,能够有效指导工程现场建设的资料仍然不足。为此,依据室内试验结果,分析了温度场与应力场对碳质千枚岩应力应变曲线影响;基于M-C准则与H-B准则分别建立热力耦合作用下碳质千枚岩强度演化计算方法,即Mohr-Coulomb-Thermal (M-C-T)法和Heok-Brown-Thermal (H-B-T)法,并对比分析两者间误差,为软岩区隧洞掘进与支护施工建设给予参考。

1 热力耦合室内试验

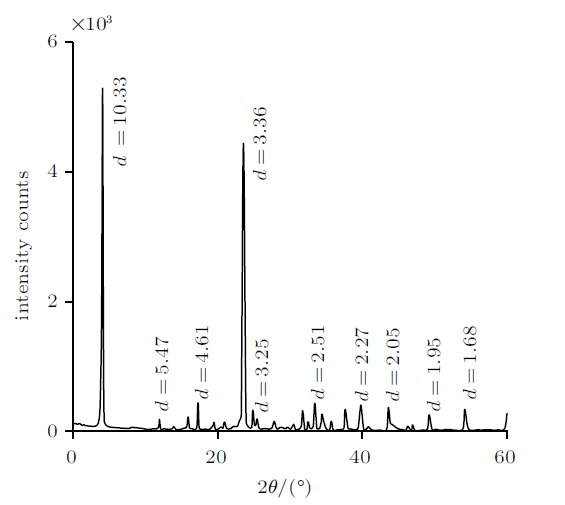
四川西部某大(2)型水电站枢纽布置圆形有压引水隧洞,其平均埋深为400 m,最大埋深超过1000 m;地层以黑色碳质千枚岩为主,实测最高地温达47.2℃。室内试验所用岩样为现场钻孔岩芯,经X射线衍射图谱(见图1)分析,岩样主要成分为黑云母68%,伊利石18%,石英10%,膨胀性不显著。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 岩样X射线图谱

Fig.1 X-ray atlas of rock samples

采用自带温控设备与数据采集系统的MTS815程控伺服岩石力学试验机进行热力耦合的单轴和常规三轴试验,设定温度与应力2因素4水平共计16组试验,测定碳质千枚岩在热力耦合下应力应变曲线与峰值强度分布。根据引水隧洞埋深,设定0 MPa,10 MPa,20 MPa与30 MPa四种工况静水压力($\sigma_{3})$,载荷施加速率为0.005 mm/s;考虑施工过程采用冰水混合物对围岩体降温的作法,设定试验温度($T)$为0${^\circ}$C,20${^\circ}$C,40${^\circ}$C与60${^\circ}$C四个等级,温度施加速率为1.0 ${^\circ}$C/min。试样尺寸为直径50$\pm$0.5 mm,高100$\pm$0.5 mm的圆柱体,试验过程为：(1)先将环境设定为20${^\circ}$C (常温),放置试样;(2)施加静水压力至预定值,并保持2 h;(3)调节温度至预定值,并保持恒温5 h;(4)施加轴向载荷直至试样破坏。

2 热力耦合作用分析

2.1 应力-应变曲线

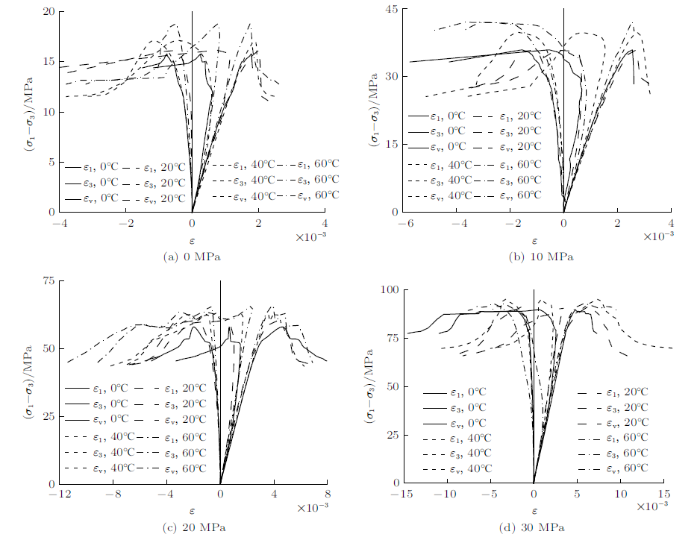
整理试验结果,在同一坐标系下绘制各温度-围压影响下试样的偏应力($\sigma_{1}-\sigma_{3})$随应变$\varepsilon $ (轴向应变$\varepsilon_{1}$,侧向应变$\varepsilon_{3}$与体积应变$\varepsilon_{\rm v})$曲线,见图2。从图2可知,依据峰值应力前后曲线性态,将热力耦合作用下碳质千枚岩($\sigma_{1}-\sigma_{3})$-$\varepsilon$曲线大致分为脆性破坏与延性破坏两类^[12]。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 碳质千枚岩应力-应变曲线

Fig.2 Stress-strain curves of carbonaceous phyllite

(1) 脆性破坏曲线。随着轴向载荷增加,试样发生弹性变形,($\sigma _{1}-\sigma_{3})$与$\varepsilon$均呈线性缓慢增加;当岩石变形进入屈服阶段,$\varepsilon_{1}$持续增大,但$\varepsilon_{3}$增大的幅度大于$\varepsilon_{1}$,$\varepsilon_{\rm v}$存在减小的趋势;岩石达到峰值强度后发生破坏,($\sigma_{1}-\sigma_{3})$急剧减小,$\varepsilon_{3}$大于$\varepsilon_{1}$,$\varepsilon_{\rm v}$小于0,试样出现了扩容现象,残余强度不显著,如图2(a)中0${^\circ}$C,20${^\circ}$C,40${^\circ}$C及60${^\circ}$C的曲线,图2(b)中0${^\circ}$C,20${^\circ}$C及40${^\circ}$C的曲线,图2(c)和图2(d)中0${^\circ}$C曲线。

(2) 延性破坏曲线。峰前曲线形状与脆性破坏相似,峰后曲线($\sigma_{1}-\sigma_{3})$随$\varepsilon$增加呈变化幅度较小或者缓慢跌落,$\varepsilon_{3}$与$\varepsilon_{\rm v}$增加的幅度大于$\varepsilon_{1}$,扩容现象较为显著,存在残余强度,如图2(c)中40${^\circ}$C及60${^\circ}$C的曲线,图2(d)中40${^\circ}$C及60${^\circ}$C的曲线。

从($\sigma_{1}-\sigma_{3})$-$\varepsilon$曲线可知,碳质千枚岩在低围压与低温度呈脆性破坏,残余强度不显著;在高围压与温高度作用时呈延性破坏,存在明显的残余强度。两种破坏模式下体积在峰后均增大,出现了显著扩容现象。

2.2 Mohr-Coulomb强度准则

M-C强度准则是基于各向同性介质微元体所受剪切应力$\tau $达到其极限应力$\tau_{\max}$时发生破坏并逐渐发展演化为整体破坏而建立的计算方法,其表达式为

(1)$ \tau =c+\sigma \tan \varphi $

式中,$\sigma $为正应力,MPa;$c$为黏聚力,MPa;$\varphi$为内摩擦角,($^\circ$)。

常规三轴条件下根据摩尔圆中角度换算关系,将式(1)变换为

(2)$ \sigma_{\rm f} =M\sigma_{3} +N $

式中,$\sigma_{\rm f}$,$\sigma_{3}$分别为峰值强度与围压;$M$,$N$为系数

(3)$ M=\tan^{2}\left( {45^{\circ }+\varphi /2} \right) $

(4)$ N=2c\cos \varphi /\left( {1-\sin \varphi } \right) $

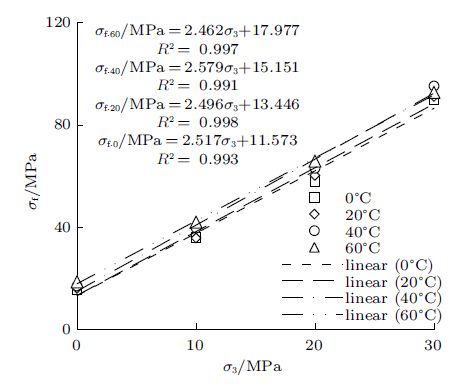
整理图2中碳质千枚岩单轴与三轴的峰值应力数据,依据式(2)采用最小二乘法拟合得到系数$M$与$N$值,见图3;再利用式(3)与式(4)便求得M-C准则下强度指标$c$与$\varphi$。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 M-C-T法$\sigma_{\rm f}-\sigma_{3}$分布

Fig.3 Distribution of $\sigma_{\rm f}-\sigma_{3}$ for M-C-T method

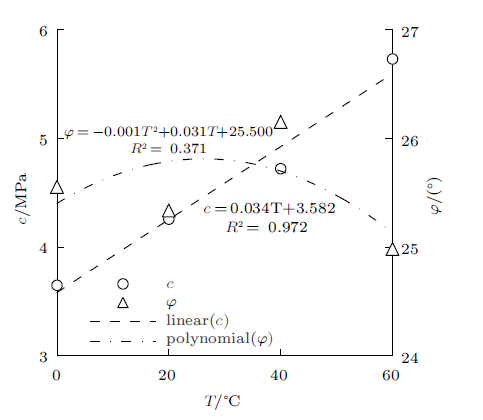
从图3可知,热力耦合作用下碳质千枚岩$\sigma_{\rm f}$与$\sigma_{3}$线性关系显著。为进一步探讨温度场作用,在同一坐标系下绘制$c$与$\varphi$随$T$的分布,见图4。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 $c$与$\varphi $随$T$变化曲线

Fig.4 Curves of $c$ and $\varphi $ with $T$ changing

从图4可知,$c$随$T$升高呈线性增大,$\varphi$的变化规律不明显,仍采用线性与二次函数分别拟合$c-T$与$\varphi$-$T$分布,见式(5)与式(6)。

(5)$\hspace{-5mm}c=0.034T+3.582,\ \ {R^{2}=0.972}$

(6)$ \hspace{-5mm}\varphi =-0.001T^{2}+0.031T+25.500,\ \ {R^{2}=0.371} $

将式(3)~式(6)代入式(2)得到基于M-C准则考虑热力耦合作用下碳质千枚岩破坏强度$\sigma_{\rm f,M-C}$计算方法,记为M-C-T法,即

(7)$ \left.\begin{array}{l}\sigma_{\mathrm{f}, \mathrm{M}-\mathrm{C}}=\tan ^{2}\left(45^{\circ}+\frac{\varphi}{2}\right) \sigma_{3}+ \\\frac{2 \cos \varphi}{(1-\sin \varphi)}(0.034 T+3.582) \\0 \leqslant \sigma_{3} \leqslant 30 \mathrm{MPa} \\0 \leqslant T \leqslant 60^{\circ} \mathrm{C}\end{array}\right\} $

式中$\varphi $采用式(6)计算,若不考虑$T$对$\varphi $影响,$\varphi $取25.5$^\circ$ (即均值)。

2.3 Heok-Brown强度准则

H-B准则是根据岩体性质并分析了大量岩体与岩块破坏时试验数据后,总结得到了主应力间关系的经验方程,即

(8)$ \left( {\frac{\sigma_{\rm f} -\sigma_{3} }{\sigma_{\rm c} }} \right)^{2}=m\frac{\sigma_{3} }{\sigma_{\rm c} }+s $

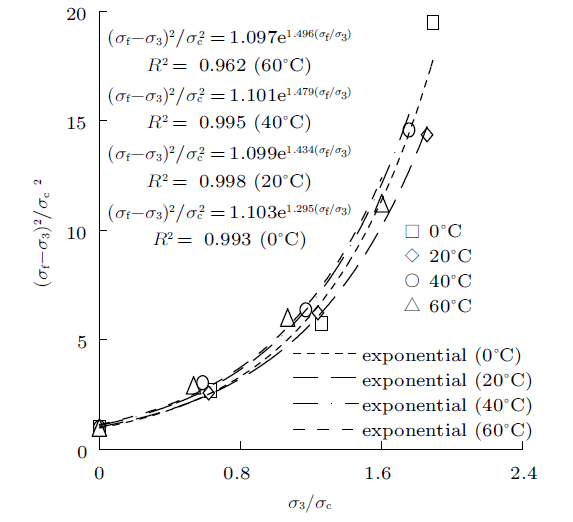
式中,$\sigma_{\rm c}$为岩块单轴抗压强度;$m$是与岩石种类有关的参数,$s$是与岩体结构面性质有关的参数。利用式(8)整理试验数据时发现($\sigma_{\rm f}-\sigma_{3})^{2}$/$\sigma_{\rm c}^{2}$与$\sigma_{3}$/$\sigma_{\rm c}$之间指数关系更优于线性关系,见图5。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 H-B-T法$\sigma_{\rm f}-\sigma_{3}$分布

Fig.5 Distribution of $\sigma_{\rm f}-\sigma_{3}$ for H-B-T method

从图5可知,热力耦合作用下碳质千枚岩强度演化规律可概化为式(9)形式的数学表达。

(9)$\left( {\frac{\sigma_{\rm f} -\sigma_{3} }{\sigma_{\rm c} }} \right)^{2}=h{\rm e}^{n\frac{\sigma_{3} }{\sigma_{\rm c} }}$

式中$h$与$n$是温度作用下与岩石种类和岩体结构面性质有关的参数。

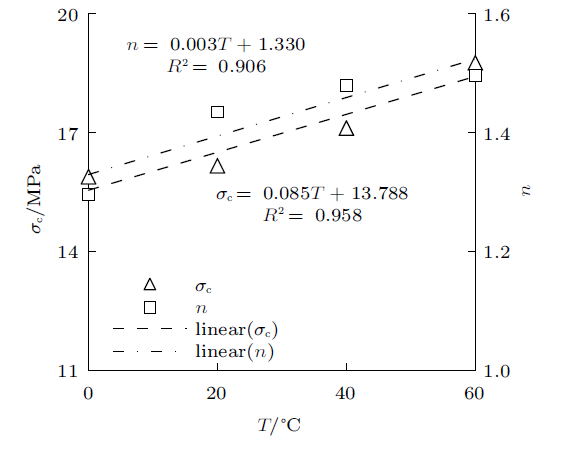
整理试验数据,发现不同$T$和$\sigma_{3}$下$h$变化较小;在H-B准则中,$m$表征岩块的强度特征,同一种类岩块,$m$取值范围较小,则将参数$h$与$m$的内涵视为相似,均为与岩石种类相关的参数。因此,此处取1.100 (均值);$\sigma_{\rm c}$和$n$均与$T$呈显著的线性关系,见图6,得到其拟合表达式为

(10)$ \sigma_{\rm c} =0.085T+13.788,\ \ {R^{2}=0.958} $

(11)$ n=0.003T+1.330,\ \ {R^{2}=0.906} $

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 $\sigma_{\rm c}$与$n$随$T$变化曲线

Fig.6 Curves of $\sigma_{\rm c}$ and $n$ with $T$ changing

将式(10)与式(11)代入式(9)得到基于H-B准则考虑温度与围压耦合作用下碳质千枚岩破坏强度$\sigma _{\rm f,H-B}$计算方法,记为H-B-T法,即

(12)$\left.\begin{array}{l}\sigma_{\mathrm{f}, \mathrm{H}-\mathrm{B}}=\sigma_{3}+(0.089 T+14.461) \mathrm{e}^{\frac{0.003 T+1.330}{0.170 T+28.922} \sigma_{3}} \\0 \leqslant \sigma_{3} \leqslant 30 \mathrm{MPa} \\0 \leqslant T \leqslant 60^{\circ} \mathrm{C}\end{array}\right\}$

3 计算方法评价

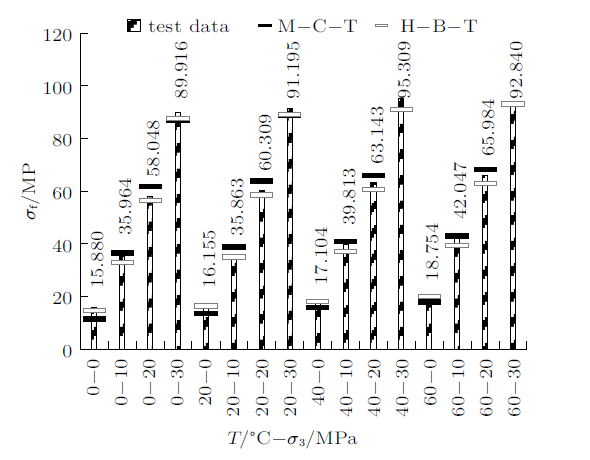
将$\varphi $取25.5$^\circ$,$h=1.10$,再取相同$T$与$\sigma_{3}$采用式(7)和式(12)进行计算,得到$\sigma_{\rm f,M-C}$与$\sigma_{\rm f,H-B}$计算值;采用式(13)分析两种模型与试验值的相对误差$E_{\rm rr}$。图7为不同工况下热力耦合作用下碳质千枚岩试验值$\sigma_{\rm f}$,$\sigma_{\rm f,M-C}$与$\sigma_{\rm f,H-B}$条形分布图,图8为各自$E_{\rm rr}$在试验值两侧的分布。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 $\sigma_{\rm f}$,$\sigma_{\rm f,M-C}$与$\sigma_{\rm f,H-B}$分布

Fig.7 Distribution of $\sigma_{\rm f}$,$\sigma_{\rm f,M-C}$ and $\sigma_{\rm f,H-B}$

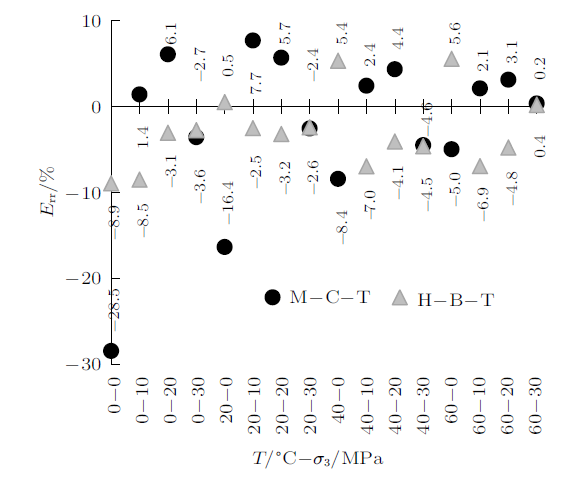
由图7可知,$\sigma_{\rm f}$,$\sigma_{\rm f,M-C}$与$\sigma_{\rm f,H-B}$三者间数值差异较小,这说明M-C-T法和H-B-T法均能较好地量化热力耦合作用下碳质千枚岩强度演化规律;从图8中$E_{\rm rr}$大小及分布可知,M-C-T法计算值在试验值两侧均匀分布,计算误差介于$-$28.5%~7.7%,离散程度较大;H-B-T法计算值大多均分布于试验值偏小一侧,计算误差介于$-$8.9%~5.6%,离散程度较小。因此,与M-C-T法相比,H-B-T法计算结果稳定性更高,且更偏向于安全。

(13)$E_{\rm rr} =\frac{\mbox{试验值}-\mbox{计算值}}{\mbox{试验值}}\times10\%$

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 M-C-T法和H-B-T法的$E_{\rm rr}$分布

Fig.8 $E_{\rm rr}$ distribution of M-C-T method and H-B-T method

4 结论

(1) 温度场与应力场影响了碳质千枚岩破坏模式,在围压与温度均较低时呈脆性破坏,较高时逐渐转为延性破坏,存在残余强度,且峰后扩容现象显著。

(2) 根据峰值强度与围压关系,发现黏聚力、单轴抗压强度和参数$n$随温度升高呈线性增大,内摩擦角受温度影响不显著;基于Mohr-Coulomb准则与Heok-Brown准则,分别建立了热力耦合作用下碳质千枚岩破坏强度计算方法,即M-C-T法和H-B-T法。

(3) 通过计算,两种方法计算值均与试验值分布相似,这说明M-C-T法和H-B-T法都能较好地量化热力耦合作用下碳质千枚岩强度演化规律;误差分析表明,M-C-T法计算误差介于$-$28.5%~7.7%,离散程度较大;H-B-T法计算误差介于$-$8.9%~5.6%,离散性较小,且更偏向于安全。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

薛翊国, 孔凡猛, 杨为民

等.

川藏铁路沿线主要不良地质条件与工程地质问题

岩石力学与工程学报, 2020, 39(3):445-468