水上迫降是指陆基飞行器在水面上的可控紧急降落,属于典型的入水冲击问题,世界各国民用运输机适航条例均要求跨水域飞行必须通过水上迫降适航审定。早在1929年,Karman[1]就对水上飞机入水冲击的水载荷进行过理论研究,早期众多理论方法都集中于研究二维物体垂直入水问题,但对于复杂三维民用飞机的水上迫降问题,理论分析无法得到应用。1940年代开始,国外相继开展了一系列动力相似模型试验,用以研究民用飞机水上迫降特性[2-3]。然而动态模型试验具有较强的随机性,且无法准确模拟气动力的影响,同时也无法较好地解释迫降过程中的作用机理。20世纪后期,随着计算理论和计算机硬件技术的发展,成本低廉且展示度高的数值仿真方法逐步取代了模型试验。越来越多的研究通过数值仿真方法模拟飞机水上迫降,在此过程中不断总结提炼[4],逐渐完善仿真方法,使之成为未来研究水上迫降问题的重要手段。
绝大部分的数值仿真均基于以下几类方法:面元法(panel method, PM),有限元法(finite element method, FEM),光滑粒子水动力学法(smooth particle hydrodynamics, SPH) 和有限体积法(finite volume method, FVM)。2001年,Vladimir等[5]基于动量守恒原理采用PM对福克614飞机的水上迫降压力、变形和漂浮特性开展了研究。2008年,Shoji等[6]基于LY-DYNA软件使用FEM对缩比机身等直框段垂直入水进行了模拟,压力峰值数据和试验吻合较好但时间历程相差较大。2010年,贺谦等[7]研究了水平速度、下沉率、俯仰角对迫降时飞机机身载荷的影响,但仿真方法未经验证。2013年,徐文岷等[8]采用FEM考虑了水、空气和飞机结构之间的耦合作用,对民用支线飞机水上迫降进行了模拟,但得到的入水初期运动姿态与试验相差较大。SPH方法由于其不依赖网格的特点优势在水上迫降仿真中得到了应用。2006年,Climent等[9]针对CN-235飞机的研究表明在水上迫降这一类以水平速度为主导的运动中,以本构方程为控制方程的SPH法无法模拟出气穴效应和负压力,从而影响对运动姿态和冲击力的模拟。之后,文献[10,11,12]开发了基于弱可压缩连续方程为控制方程的SPH,模拟负压的精度得到了提升。
PM计算的原理一般是基于动量守恒或势流理论,忽略黏性、可压缩性、重力和气垫效应等等,多用于简单外形的物体入水问题,在精确描述民用飞机水上迫降动力学问题时存在一定难度。FEM绝大部分基于商用有限元分析软件,对于气动力的模拟存在困难,另外,计算结果依赖于流固耦合算法,常见的问题是容易引起流体渗漏,导致流体和固体载荷不统一。SPH避免了由于网格划分产生的问题,但在流体与固体的边界处理上存在较大难度,在模拟精度上存在劣势,且建模复杂度较高。实际水上迫降过程中,飞行速度必须维持在可以保持飞机平稳下降的水平,气动力的影响无法忽略。此外,由空气和水面压差导致的机身尾部的吸力也是影响迫降运动状态和全机载荷的重要因素,因此FVM具有较大的优势。
2007年,Streckwall等[13]使用基于FVM和流体体积(volume of fluid, VOF)法的COMET软件对飞机水上迫降过程进行了模拟,对比试验表明计算结果较为准确,并直观体现了飞机入水过程中的水面运动和飞机表面压强分布;2012年,Zhang等[14]模拟了一种支线客机的水上迫降过程,表明吸力对于飞机水上迫降的姿态影响较大,且空气模型是吸力产生的必要条件。同一时期,屈秋林等[15]和Guo等[16]详细地研究了尾吊高平尾、翼吊低平尾和翼身融合三种不同布局飞机的水上迫降特性,认为正常布局飞机的低平尾具有抑制飞机过度上仰的作用,从而有利于减缓过载和局部压力。2019年,吴宗成等[17]基于FVM采用滑移动网格研究了波浪对水上迫降特性的影响。由于水上迫降过程中的水平位移较大,目前基于FVM的方法大多采用动网格实现对运动过程的模拟,通过网格变形和重构模拟飞机和计算域的运动,需消耗庞大的计算资源。本文在已有FVM方法的基础上采用全流场运动网格的方法,添加约束保持水面高度不变,使流场相对水面自由运动,大大缩减了计算量。首先通过典型算例对该方法进行验证,然后模拟分析了某型飞机的水上迫降运动过程。
1 仿真方法
本文采用ANSYS FLUENT软件,基于非定常RANS方程,使用加强壁面处理的可实现 $k$-$\varepsilon$湍流模型,压力速度耦合采用SIMPLEC算法。各控制方程中扩散项采用二阶中心差分格式离散,动量方程的对流项采用三阶守恒律的单调迎风格式,湍动能、湍流耗散率和能量方程对流项采用二阶迎风格式离散,非定常项采用一阶隐式格式离散,水气体积分数离散采用Modified HRIC格式 以精确捕捉水气界面。采用全流场运动网格模拟模型和周围的流场运动。在空气和水面两相流的界面定义中运用了VOF模型,即同一个网格内空气和水的体积分数之和为1,对于第1相流空气的体积分数$v_{1}$,如果一个网格中的$v_{1}=0$表示不存在空气,$v_{1}=1$表示该网格中只有空气,$0<v_{1}<1$则该网格中同时存在空气和水。使用用户自定义函数定义水面位置和流场初始压力分布。同时使用六自由度模型求解平动和转动方程确定模型的位置和姿态。当模型为对称运动时,可将侧滑和滚转方向的运动约束住,从而简化为三自由度模型,方程为
式中,$V_{i}$表示$x$或$y$方向的速度,$F_i$表示$x$或$y$方向的合力,$t$表示时刻,$m$表示质量,$M$表示俯仰力矩,$I$表示俯仰惯量,$\theta$表示俯仰角,$n$和$n-1$分别表示当前和上一个时间步长。由此可获得模型当前的位置和姿态为
2 二维垂直入水算例
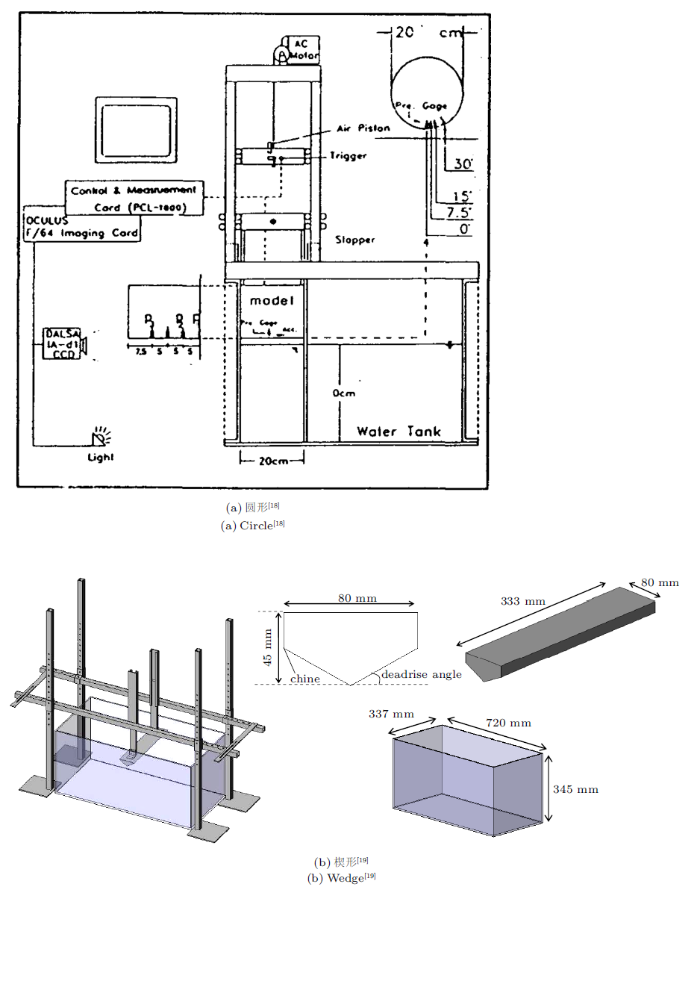
2.1 算例参数
图1
2.2 求解过程
2.2.1 流场设置
对计算域进行网格划分,由于模型均左右对称,因此计算时采用半模,对模型附近尤其是底部与水面交界处的网格进行适当加密。对称面采用对称边界条件,模型为无滑移壁面条件,其余边界均为压力入口边界条件。计算域的网格划分结果如图2所示。
图2
2.2.2 时间步长设置
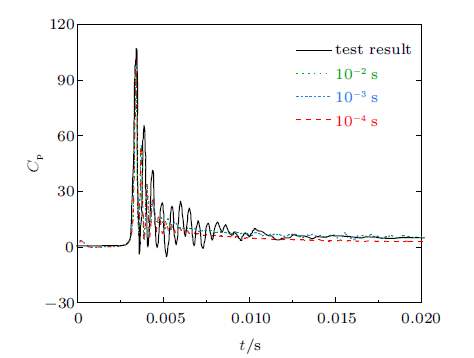
采用第1节中的方法进行求解参数设置。由于入水过程为动态变化过程,时间步长的设置需要兼顾对运动特征的捕捉、计算稳定性以及计算效率。为了保证计算稳定性,需在每一个时间步长内迭代计算达到收敛,然后开始下一个时间步长。因此时间步长应选定一个合理的区间,太大或太小都可能会导致无法收敛。在确定数值时一般会参考特征长度除以特征速度得到的特征时间,在此基础上低两个数量级。另外由于入水冲击过程中速度变化较为剧烈,因此可将时间步长设置为可变的,设定最大和最小时间步长以及步长变化系数,计算过程中根据收敛情况自动更改时间步长。以二维圆形算例为对象,特征长度为0.2 m,特征速度为0.989 m/s,计算特征时间约为0.2 s,将初始时间步长设置为10$^{-4}$ s,分别对最大时间步长10$^{-2}$ s,10$^{-3}$ s,和10$^{-4}$ s进行影响研究。图3所示为不同时间步长计算得到的圆弧角0$^\circ$ (即最低点)压力系数$C_p$与试验结果的对比,可以看出,不同时间步长下,对于压力峰值和变化趋势的捕捉结果基本一致,在入水后期由于速度大幅降低,压力数值较小,计算结果出现小幅波动,但此时并不是冲击问题的关注点,影响可以忽略。综上,将时间步长设置为可变的可以降低计算结果对时间步长的依赖性,同时保证计算精度。考虑到计算效率,可以适当增加最大时间步长,因此在后续的计算中,采用初始时间步长10$^{-4}$ s,时间步长范围设定为10$^{-3}$ s~10$^{-6}$ s。
图3
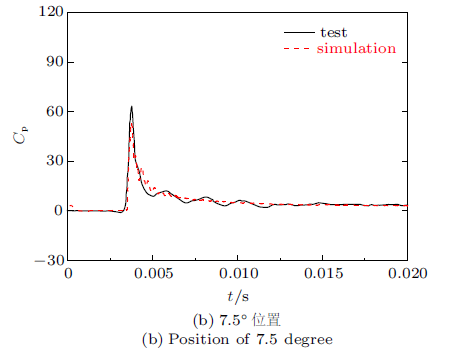
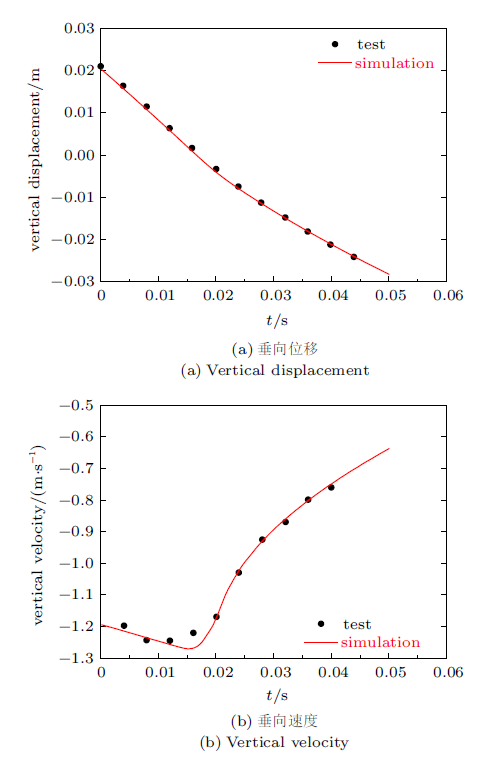
2.3 仿真结果
图4
图5
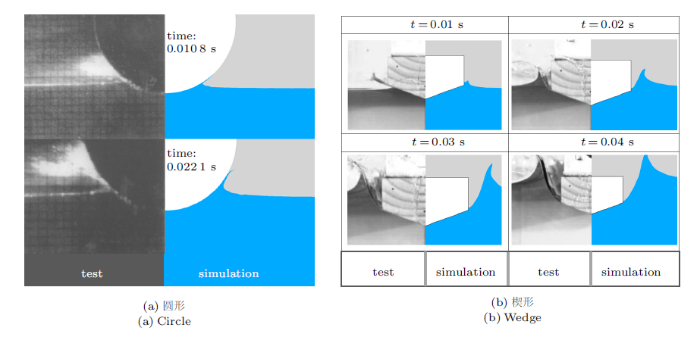
在工程实际应用中,不仅关心飞机在水上迫降过程中运动和受力情况,同时也需关注水面变形情况,为确定水线位置以及后续的漂浮特性提供依据。因此能否准确模拟水面位置和动态变化趋势也十分重要。图6所示为仿真与试验中模型入水过程中水面变化情况的对比,水面的变形过程得到了很好的复现。虽然无法捕捉到液体的破碎和喷溅,但这些现象对于宏观运动趋势影响较小,在更关注运动姿态和受力形式的飞机水上迫降问题研究中可以忽略。
图6
3 三维水上迫降算例
3.1 算例参数
图7
3.2 求解过程
由于试验时飞机为对称运动,建模时采用半模,机体表面网格如图8所示,对称面采用对称边界条件,机身表面采用无滑移边界条件,其余边界均为压力入口边界条件。所有网格均为六面体结构网格,网格总数约240万,计算初始时间步长为10$^{-4}$ s。
图8
3.3 计算结果
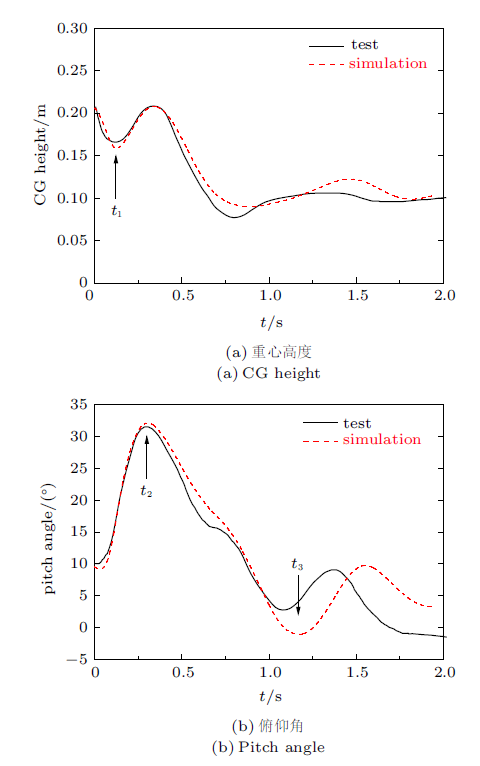
图9所示为模拟与试验的对比结果,其中实线表示试验数据,虚线表示仿真结果。可以看出俯仰角和重心高度的变化趋势总体上非常吻合。飞机开始触水即0~$t_{1}$时刻,重心高度随着入水深度的增加逐渐降低,之后由于俯仰角逐渐增大,而重心位置靠近前机身,因此高度也随之增加。$t_{2}$时刻开始,俯仰角逐渐减小即飞机逐渐低头,飞机在气动升力和水面浮力作用下保持在水面上滑行,入水深度变化较小,高度随俯仰角的降低而减小。$t_{3}$时刻开始前机身逐渐入水,受到冲击力俯仰角略有增大,但变化幅度较小,同时飞机在浮力和重力作用下绕重心上下浮动,因此重心高度逐渐趋于稳定。
图9
4 某型支线飞机水上迫降模拟
4.1 参数设置
图10
4.2 计算结果对比
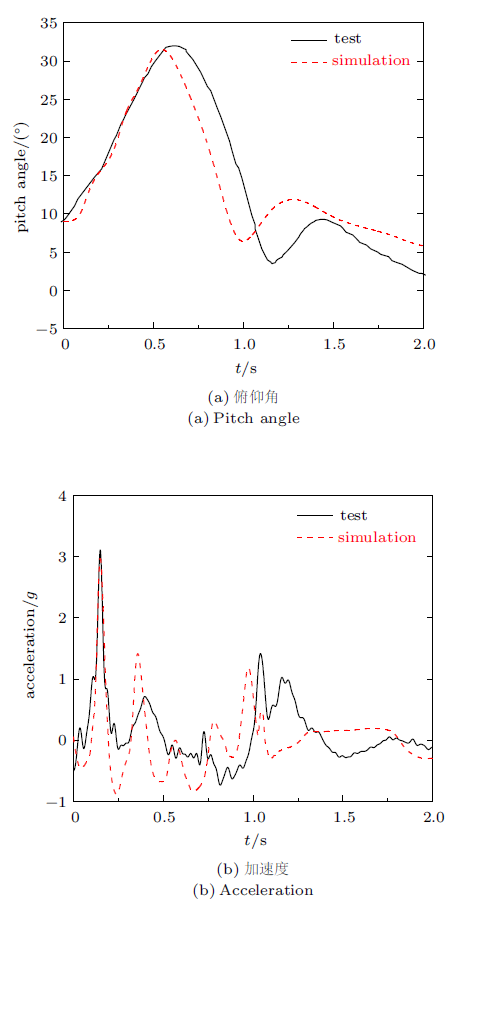
图11所示为计算得到的俯仰角和重心处垂向加速度随时间的变化曲线与试验对比结果。俯仰角变化趋势与第3节中的经典模型类似,经历了两次明显的上仰过程。重心处垂向加速度在入水后约0.15 s出现峰值,随后出现波动并逐渐趋于0$^\circ$。俯仰角和加速度峰值的模拟数据与试验值误差分别为1.5%和4.5%,表明模拟结果能够较好地反映水上迫降运动过程和模型整体受力情况。
图11
4.3 运动过程和受力分析
4.3.1 运动过程
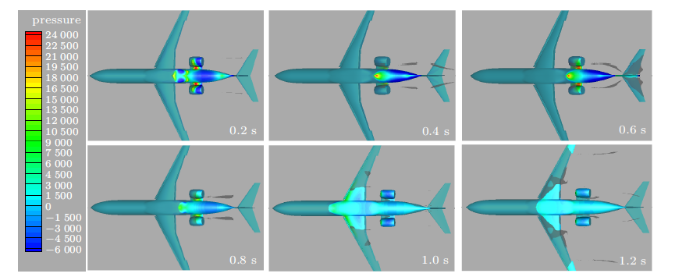
图12
图12
迫降过程中的水线位置和压力分布
Fig.12
Water surface position and pressure distribution during ditching
0.6 s左右俯仰角达到第一个峰值约32$^\circ$。由于该支线飞机采用T型尾翼,高置平尾,因此即使俯仰角到达峰值时平尾仍然位于水面以上,局部喷溅的水花对平尾的冲击力较小,无法起到抑制俯仰角继续上仰的作用。0.6 s以后,由于巨大的水阻力使得滑行速度迅速降低、后体吸力减弱,同时中后机身以及发动机短舱着水部位受到较大的冲击力,产生低头力矩,从而使得飞机逐渐低头。过程中飞机持续下沉,中后机身和发动机不断排开水面,冲击力出现小幅增大。
0.8 s~1.0 s之间,随着飞机的低头前机身逐步入水,在此过程中受到较大的冲击力产生抬头力矩,使得1.0 s以后加速度和俯仰角均出现第二次峰值,但由于此时速度已经大幅度降低,第二次峰值相较第一次有明显降低。此后飞机逐渐趋于稳定,1.2 s时机身底部的压力分布已经显著降低且分布较为均匀。
4.3.2 受力分析
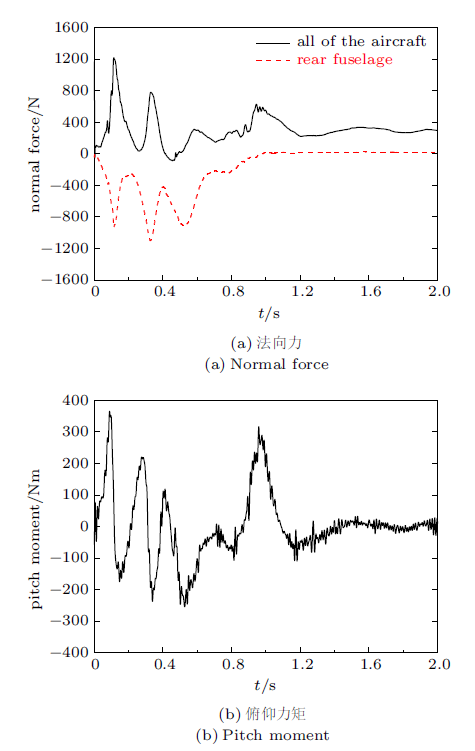
图13(a)给出了整个机身以及机身尾部受到的法向力随时间的变化曲线,$t=0$ s时刻机体开始着水,可以看到法向合力的变化趋势与图11(b)的过载曲线一致,并且机身尾部受力始终为负且峰值达到约$-$1100 N,后体吸力作用明显。在着水1.2 s以后受力逐渐趋于稳定,表明飞机逐渐停止上下沉浮运动。图13(b)所示为飞机的俯仰力矩随时间的变化曲线,使飞机抬头为正。入水初期俯仰力矩迅速增加,飞机出现第一次抬头,随后俯仰力矩产生波动并逐渐减小,对应图11(a)中抬头趋势逐渐平缓,0.6 s以后低头力矩逐渐减小,对应图11(a)中低头趋势也逐渐平缓。0.8 s以后,与运动过程分析一致,俯仰力矩再次增加从而产生第二次抬头运动,1.2 s后俯仰力矩趋于0表明飞机逐渐停止俯仰运动,达到静止状态。
图13
5 结论
通过对圆形和楔形垂直入水以及三维飞机入水试验的模拟,基于全流场运动网格的CFD水上迫降仿真方法得到了验证。利用该方法研究了某型支线飞机水上迫降的运动和受力特性。结果表明仿真得到的俯仰角和加速度数据均与试验值相近,对后体吸力的准确模拟证实了其对于迫降运动状态和受力特点的重要影响。通过对仿真结果的进一步分析表明,尾吊-高平尾布局的支线飞机在水上迫降时,后机身和发动机短舱底部的后体吸力会导致飞机产生明显的抬头,由于平尾高置无法抑制抬头,俯仰角峰值会达到30$^\circ$以上,入水后期水阻力使得速度减小,从而减弱吸力,使得飞机逐渐低头并在较小的波动后逐渐趋于平稳。针对民用飞机水上迫降特性的研究目的,本文目前仅完成了方法的验证和典型迫降工况的分析,对于俯仰角、气动力等不同因素的影响研究还需持续开展。
参考文献
The impact on seaplane floats during landing
Ditching tests with 1/16-size models of the Army B-17 airplane in Langley tank number 2 and on an outdoor catapult
Experimental investigation of the effect of rear-fuselage shape on ditching behavior
数值计算技术在飞机水上迫降中的应用
Application of computational fluid dynamics in the planned ditching of a transport airplane
Numerical simulation of emergency landing of aircraft on a plane water surface. 2nd International Conference on High-Perform
Hydrodynamic impact estimation of transport fuselage structure with vertical drop water impact tests
基于ALE方法的飞机水面降落过程
On dynamic structural response of an airplane landing onto water
民用飞机水上迫降数值模拟分析
Numerical simulation and analysis on civil aircraft ditching
Aircraft ditching numerical simulation
Innovative SPH methods for aircraft ditching
Development of a smoothed particle hydrodynamics method and its application to aircraft ditching simulations
Towards the modeling of the ditching of a ground-effect wing ship within the framework of the SPH method
Ditching often takes place for a ground-effect wing (WIG) ship. During the ditching, the extreme load developed by water impacts may cause damages to structures, posing a great threat to the safety of crew and passengers. In the paper, a weakly compressible smoothed particle hydrodynamics (SPH) model combined with enhanced numerical techniques has been adopted to tackle the ditching problems. In order to handle the motion of a rigid body in the three-dimensional ditching problems, the six degrees-of-freedom (6-DOF) equations of motion are incorporated into the SPH scheme. The accuracy of the SPH model is validated through two benchmarks, respectively, the two-dimensional wedge water entry and the three-dimensional stone-skipping. The former is aimed to validate the prediction of pressures during the free surface impact while the latter is a good case for testing the coupling motions of the rigid body. Furthermore, the ditching of the real scale WIG ship under different conditions is simulated with the established SPH model, through which some useful conclusions are drawn.
Aircraft ditching: a free surface/free motion problem
The suction force effect analysis of large civil aircraft ditching
某型客机水上迫降的着水冲击力学性能数值研究
Numerical research on water impact performance of typical civil aircraft ditching
Effect of pitch angle on the initial stage of a transport aircraft ditching
滑移动网格在波浪水面迫降数值模拟中的应用
Application of sliding dynamic gird to wavy water ditching simulation
Simultaneous measurements of water impact on a two-dimensional body
Water impact investigations for aircraft ditching analysis. [Master Thesis]