力学与实践, 2022, 44(1): 22-29 DOI: 10.6052/1000-0879-21-356

应用研究

湍流边界层大尺度相干结构空间相位平均拓扑1)

岳巾会,*,2), 范子椰*, 姜楠,*,†,3)

*天津大学机械工程学院,天津 300354

†天津市现代工程力学重点实验室,天津 300354

SPATIAL PHASE MEAN TOPOLOGY OF LARGE-SCALE COHERENT STRUCTURES IN TURBULENT BOUNDARY LAYER1)

YUE Jinhui,*,2), FAN Ziye*, JIANG Nan,*,†,3)

*Department of Mechanics, Tianjin University, Tianjin 300354, China

†Tianjin Key Laboratory of Modern Engineering Mechanics, Tianjin 300354, China

通讯作者: 2)岳巾会,本科生,研究方向为湍流边界层实验测量。 E-mail:15142626794@163.com;3)姜楠,教授,研究方向为湍流与实验流体力学。 E-mail:nanj@tju.edu.cn

责任编辑: 胡漫

收稿日期: 2021-08-23   修回日期: 2021-09-25  

基金资助: 1)国家自然科学基金(11732010)
国家自然科学基金(11972251)
国家自然科学基金(11872272)
中德科学基金国际交流合作项目(GZ1575)

Received: 2021-08-23   Revised: 2021-09-25  

作者简介 About authors

摘要

湍流边界层大尺度相干结构(large-scale coherent structure,LSCS)是目前湍流边界层研究的热点之一。湍流边界层中存在大尺度相干结构均是通过各种谱的低波数峰值证实的,而对大尺度相干结构各种物理量的空间拓扑形态及其发展演化规律还缺乏研究。应用高时间分辨粒子图像测速多相机阵列系统,测量湍流边界层大尺度相干结构各种状态的空间拓扑。实验雷诺数$Re_{\tau} =422$,采用沿流向方向按顺序排列四个高速相机同步拍摄,得到约$6.7\delta\times 1.2\delta$的大视场。在所有法向层沿流向方向进行空间多尺度连续小波变换,根据分尺度小波系数得到湍动能随流向尺度和法向位置的分布,根据各尺度小波系数的正负极值点检测各尺度相干结构喷射和扫掠的拓扑中心,使用条件采样和空间相位平均的方法测得各尺度相干结构喷射和扫掠阶段的空间拓扑形态,分别得到喷射与扫掠事件的脉动速度矢量、展向涡量、流线等物理量的空间相位平均拓扑,发现大尺度喷射和扫掠事件的结构都是多个小涡组成的大尺度涡包结构,每个小涡的流线形成鞍点和焦点组成的局部不稳定动力系统。

关键词： 湍流边界层; 大尺度相干结构; 小波变换; 相位平均

Abstract

Large-scale coherent structure (LSCS) is one of the hot topics in turbulent boundary layer research. The existence of large-scale coherent structure in turbulent boundary layer is confirmed by the low wave number peak of various spectrum, but the spatial topology of various physical quantities of large-scale coherent structure and its development and evolution law are lack of research. A multi-camera array system with time-resolved particle image velocimetry is employed to measure the spatial topology of various states of large-scale coherent structures in turbulent boundary layer. Four high-speed cameras arranged sequentially along the streamwise to obtain a field of view of about $6.7\delta \times 1.2 \delta$ sufficient to investigate the large-scale structures, where the experimental Reynolds number is $Re_{\tau}=422$. The spatial multi-scale continuous wavelet transform is carried out in all normal-wall layers along the longitudinal direction of flow, and the energy distribution along the scale and normal position is obtained according to the wavelet coefficients. The topological centers of the coherent structures are detected according to the positive maximum points and negative minimum points of the wavelet coefficients at each scale, the spatial topological morphology of the coherent structures at different scales during the eject and sweep are measured by means of conditional sampling and spatial phase averaging methods, then the spatial-phased average topologies of the fluctuating velocity vector, the spread vorticity and the streamline of the eject and sweep events are obtained respectively. It is found that the vortex structure of the large-scale eject and sweep events is a large-scale vortex packet structure composed of several small vortices, and the streamline of each small vortex forms a local unstable dynamic system composed of saddle points and focal points.

Keywords： turbulent boundary layer; large-scale coherent structure; wavelet transform; phase-lock average

PDF (28388KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

岳巾会, 范子椰, 姜楠. 湍流边界层大尺度相干结构空间相位平均拓扑1). 力学与实践, 2022, 44(1): 22-29 DOI:10.6052/1000-0879-21-356

YUE Jinhui, FAN Ziye, JIANG Nan. SPATIAL PHASE MEAN TOPOLOGY OF LARGE-SCALE COHERENT STRUCTURES IN TURBULENT BOUNDARY LAYER1). Mechanics in Engineering, 2022, 44(1): 22-29 DOI:10.6052/1000-0879-21-356

湍流边界层大尺度相干结构是目前湍流边界层研究的热点之一。相干结构又称拟序结构,湍流相干结构是对湍流本质认识的新阶段,相干结构的发现为现代湍流的控制指明了方向[1-5]。湍流是多尺度的结构组成的,在不同尺度上都存在相干结构[6-7],目前普遍认为,大尺度结构在湍流中占有比较多的动能,处于比较重要的地位,是湍流研究的重点[8-9]。目前湍流边界层中存在大尺度相干结构均是通过各种谱的低波数峰值证实的。Kim等[10]发现用热膜风速法测得的充分发展的圆管湍流流向脉动速度的前乘波谱具有两个峰值：与小尺度运动相关的高波数模态和与超大尺度相关的低波数模态。Monty等[11]发现在最大的尺度上,通道/管道流动的外部呈现双峰特征,而边界层只存在一种模态。对于大尺度相干结构各种物理量的空间拓扑形态及其发展演化规律方面的研究,姜楠等[12]用空间局部平均速度结构函数检测并提取了高时间分辨率层析粒子图像测速技术数据中相干结构的“喷射”和“扫掠”事件中的速度、涡量等物理量的空间拓扑形态。Yang等[13]利用湍流空间局部平均结构函数的概念,获得了相干结构的平均速度、速度梯度、涡量、速度变形率等一阶统计平均量的空间形态。

湍流实验测量常用方法有基于单点的热线测速(hot-wire anemometry, HWA)、激光多普勒测速(laser Doppler velocimetry, LDV)以及基于场测量的粒子图像测速技术(particle image velocimetry,PIV)方法[14-17]。HWA与LDV是空间单点的流速测量技术,测量的时间分辨率高,但不能同步测量瞬态流场的空间信息,高时间分辨率的粒子图像测速技术(TRPIV)不仅能够同步测量流场空间的空间信息,而且具有kHz的时间分辨率,能够测量湍流大尺度结构的时空发展演化规律。

小波变换是新近发展起来的一种数学方法[18-20],通过信号与一个被称为小波的解析函数进行卷积将信号在时域空间与频域空间同时进行分解,子波是在物理时间(空间)确定位置具有有限尺度的局部扰动或“小波”,在确定时刻周围一定尺度的局部范围内具有正负交替的波动性,其影响范围是有限的。小波的物理概念和局部性符合湍流中湍涡(eddy)的物理概念和局部特征。 Lumley在《A First Course in Turbulence》[21]一书中指出：“由湍谱曲线中的波数表示湍涡的大小与湍涡的局域性相矛盾,用傅里叶变换分解湍流只是因为它方便(谱易于测到),如果用湍涡代替波分解湍流场,则需要一种更高级的变换。”Lumley在1970年就对湍涡的概念有过一些设想。小波分解与Lumley当初所设想的湍流场的湍涡分解概念一致,而他曾经指出：要用湍涡的概念代替波的概念来分解湍流场,那么就需要用另一种分解代替傅里叶分解。现在看来,小波分解就是这样一种基于湍涡的物理概念对湍流进行分解的方法。因此用小波对湍流进行分解可以作为湍流的湍涡结构分解的数学模型来代替傅里叶分解,用小波分解湍流中的湍涡结构是一种客观而有效的方法。

本工作应用高时间分辨粒子图像测速多相机阵列系统得到大视场的速度场,根据小波分析能量最大尺度的小波系数的正负极值点检测大尺度相干结构不同状态的拓扑中心,使用条件采样和空间相位平均的方法测得大尺度相干结构不同演化阶段的空间拓扑形态,分别得到喷射与扫掠事件的脉动速度矢量和展向涡量等物理量的空间相位平均拓扑。

1 实验设置

1.1 实验设备与实验装置

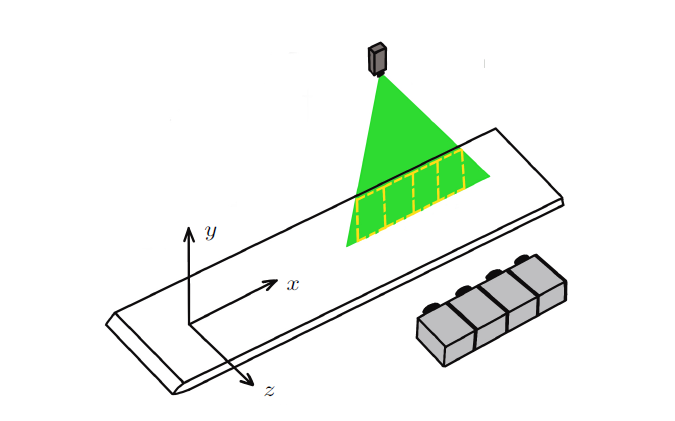
实验在天津大学流体力学实验室重力溢流式低湍流度循环水洞中进行。水洞实验段长度为4200 mm,横截面尺寸为600 mm$\times$700 mm,水洞最大流速为0.5 m/s。实验模型为长度4000 mm,宽度550 mm,厚度20 mm的有机玻璃平板。平板水平放置在水洞实验段的底面上,平板前缘为长短轴8：1的半椭圆形头部,在距离平板前缘约200 mm的表面沿展向固定直径为1.5 mm的绊线,作为扰动以加速边界层转捩,使得在实验测量的位置得到充分发展的平板湍流边界层(图1)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   实验装置示意图

Fig. 1   Schematic diagram of experimental setup


TRPIV使用的示踪粒子为直径20 $\mu$m的空心玻璃微珠。激光为Litron Lasers: LDY 300 Series,激光片光源厚度为1 mm,扩散角为30$^\circ$,使用反射镜增加激光光程,解决激光照亮区域长度偏小的问题。激光在拍摄区域有效照射宽度约为400 mm。在距平板前端2800 mm的位置依次沿流向放置四个高速相机,每个相机都固定在一个升降台和云台上,保证四个相机法向高度和拍摄距离一致,相邻相机拍摄区域在流向略有重叠,相机分辨率为1280$\times$800像素。设计一个400 mm$\times$160 mm的标定靶,既可以确定不同相机的拍摄区域的相对位置,也可以用来标定粒子图像和纠正镜头的畸变。四个相机拍摄的图像经过拼接后的实际区域大小约$(6\sim7)\delta \times (1.1\sim 1.2)\delta $ ($\delta $为边界层名义厚度)。

1.2 实验参数与平均流场

实验参数如下：实验雷诺数$Re_{\tau}=422$,自由来流速度$u_{\infty }=0.136$ m/s,采样频率$f=200$ Hz,边界层厚度$\delta=53.74$ mm,速度矢量的空间分辨率$SRV=0.9$ mm$^{2}$。

壁面摩擦速度是湍流边界层研究中的一个重要参数,但很难直接测量[22],目前壁面摩擦速度主要是通过对用黏性内尺度参数无量纲化以后的平均速度剖面的拟合算得[23]。本文采用Spalding[24]公式拟合,公式为

$y^{+}=u^{+}+\exp (-\kappa B)\cdot \\ \quad\left[\exp (\kappa u^{+}-1-\kappa u^{+}-\frac{\left(\kappa u^{+}\right)^{2}}{2}-\frac{\left(\kappa u^{+}\right)^{3}}{6}\right]\qquad$

其中,$y^{+}=y u_{\tau} / \mu$,$u^{+}=U / u_{\tau}$,$\kappa=0.41$,$B=5.0$,$\mu_{\tau}$为壁面摩擦速度,$\mu$为水的运动黏度系数,$U$为当地的流向平均速度分量。该算法计算结果的准确性和可靠性均较高[25]。对得到的粒子图像进行标定、拼接、去噪并计算得出有量纲的平均速度剖面。根据式(1),使用最小二乘方法拟合得壁面摩擦速度$\mu_{\tau}$为0.006 3 m/s。

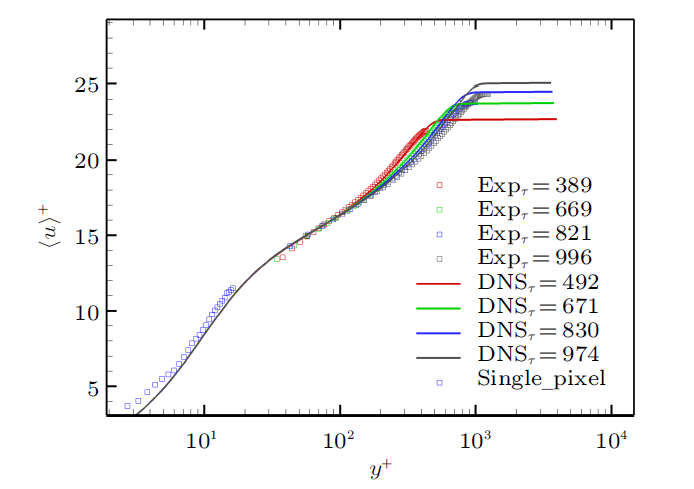
图2为用黏性内尺度参数无量纲化后的平均速度剖面。图中实线为经典的平均速度剖面对数律,显然实验获得的平均速度剖面在对数律区与对数律和直接数值模拟结果符合较好。用单像素互相关方法得到的黏性底层平均速度剖面也与黏性底层线性律符合较好。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   湍流边界层平均速度剖面

Fig. 2   Mean velocity profiles of turbulent boundary layer


2 湍流边界层脉动速度的小波分析

2.1 小波变换概述

设一维速度信号$u(x)$在小波函数$W_{ab} (x)$下的小波分析$W_{u} (a,b)$定义为

$W_{u} (a,b)=\int_{-\infty }^{+\infty } {u(x)} \overline {W_{ab} (x)} {\rm d}x$

其中小波函数族$W_{ab} (x)$是由小波母函数$W(x)$经过平移(平移因子$b$)和伸缩(尺度因子$a$)变换而来

$W_{ab} (x)=\frac{1}{\sqrt{a} }W\left( {\frac{{x-a}}{b}} \right)$

本文使用“db3”小波函数,将脉动速度分解为不同尺度部分。用小波变换对湍流边界层中不同法向位置的流向脉动速度流向空间分布进行多尺度特征分析,目的是希望用小波分析的方法获得湍流边界层流向脉动速度分尺度湍动能随尺度和法向位置变化的规律,进而提取边界层大尺度相干结构的空间尺度和形态。

2.2 能量最大准则

根据小波系数$W_{u} (a,b)$,速度信号$u(x)$的能量可以分解为

$\int_{-\infty }^{+\infty }\vert u(x){\vert }^{2}{\rm d}x= \int_0^{+\infty} \frac{E\left( {a} \right)}{a^{2}}{\rm d}a$

各尺度信号所占有能量的总和等于信号的总能量。其中

$E(a)=\frac{2}{Cw}\int_{-\infty }^{+\infty } {\vert W_{u} (a,b)\vert ^{2}{\rm d}b}$

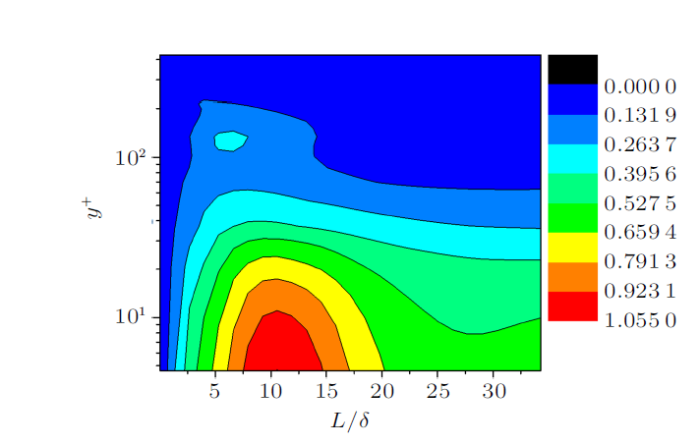
因此本文使用小波分析的能量最大准则检测相干结构。对于每一张图像,在所有法向层沿流向方向进行空间多尺度连续小波变换,根据分尺度空间小波系数得到不同尺度分量的脉动动能。然后将每一法向层不同尺度携带的流向湍动能,按照顺序排列,再对8215张图像进行求和、平均,计算每个法向位置不同尺度的湍动能随尺度和法向位置变化的云图,见图3,从图中可以看出,流场中存在着流向湍动能最大尺度,最大能量所在法向位置为$y^{+}=4.67$。流向空间尺度经过测算,约为286.56 mm,折合约为$5.33\delta$。随着法向位置远离壁面,湍动能逐渐减少。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   湍动能随尺度和法向位置分布

Fig. 3   Fluctuating kinetic energy distribution with scale and normal position


3 多尺度相干结构的检测

3.1 喷射和扫掠事件检测准则

图3的结果只说明湍流边界层近壁区也存在大尺度相干运动,但大尺度相干运动的特征形态却是很难捕捉的,文献[26,27,28,29,30]提出了从热线时间序列信号和PIV图像的多尺度小波系数检测湍流边界层大尺度相干运动的时间相位平均和空间相位平均技术。脉动速度流向空间序列的小波系数达到正的极大值代表上游低速流体喷射事件的中心,脉动速度流向空间序列的小波系数达到负的极小值代表上游高速流体扫掠事件的中心。据此总结出根据小波分析能量最大尺度的小波系数的正负极值点检测湍流相干结构喷射和扫掠事件的检测准则

$D(l,b)=\left\{ \begin{array}{lll} 1 & (\mbox{喷射}), & \mbox{$W(a,b)$ 达到正的极大值}\\ 0&,& \mbox{其他}\\ \end{array} \right.$
$D(l,b)=\left\{ \begin{array}{lll} 1 & (\mbox{扫掠}), & \mbox{$W(a,b)$ 达到负的极小值}\\ 0&,& \mbox{其他}\\ \end{array} \right.$

式中,$l$为流向空间尺度,$b$为空间流向位置,$W(a,b)$为尺度$a$在流向$b$处的小波系数。

运用空间条件相位平均方法,提取喷射和扫掠事件的脉动速度分量、展向涡量等物理量的相位平均波形。

$\left.\begin{array}{l} \left\langle {f(l_{j},x)} \right\rangle_{\rm e} =\dfrac{1}{N_{j} }\sum_{i=1}^{N_{j}} f(b_{i} +x) x\in \left[ {-\dfrac{l_{j} }{2},\dfrac{l_{j} }{2}} \right],\ {\rm while}\ D(l_{j},b_{i})=1 \\ \end{array}\right\}$
$\left.\begin{array}{l} \left\langle {f(l_{j},x)} \right\rangle_{\rm s} =\dfrac{1}{N_{j} }\sum_{i=1}^{N_{j} } f(b_{i} +x) x\in \left[ {-\dfrac{l_{j} }{2},\dfrac{l_{j} }{2}} \right],\ {\rm while}\ D(l_{j},b_{i} )=-1 \\ \end{array}\right\}$

式中,$\left\langle {f(l_{j},x)} \right\rangle_{\rm e} $和$\left\langle {f(l_{j},x)} \right\rangle_{\rm s}$分别代表喷射和扫掠事件中各物理量的相位平均波形。$f(l_{j},x)$代表脉动速度分量、涡量等物理量。$b_{i}$代表检测到喷射或扫掠事件的流向位置,$l_{j} $代表流向空间尺度,$N_{j}$代表检测到喷射或扫掠事件的次数。

对于能量最大的第10尺度,选取满足条件(6a)的空间点位置,以这些点为中心分别切出256$\times$64网格的图像,将这些图像上对应的物理量进行相位对齐叠加平均,得到喷射事件的空间条件相位平均拓扑。选取满足条件(6b)的空间点位置,以这些点为中心分别切出256$\times$64网格的图像,将这些图像上对应的物理量进行相位对齐叠加平均,得到扫掠事件的空间条件相位平均拓扑。由于第4尺度、第6尺度、第7尺度、第8尺度结构在湍流边界层中占有比较多的湍动能,是湍流边界层中起主要作用的关键结构,结果比较具有代表性,是本文分析研究的主要对象,具有比较强的规律性,因此本文对这些尺度也进行空间条件相位平均,分别得到对应的喷射和扫掠事件的空间相位平均拓扑。

3.2 检测结果分析

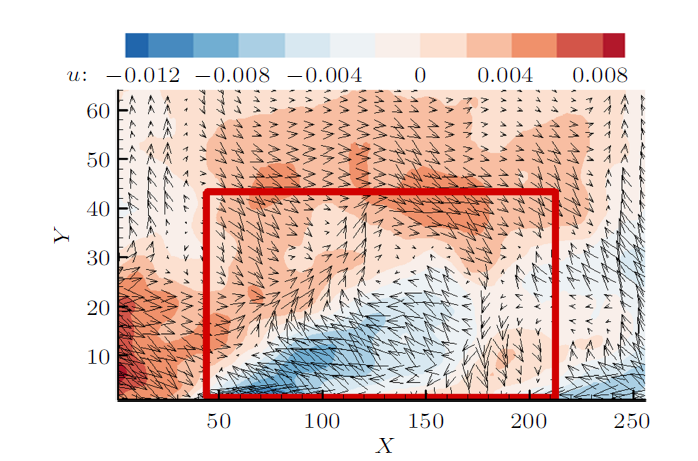
首先分析能量最大的第10尺度。图4是第10尺度喷射过程脉动速度矢量图,红色框内低速流体的流向脉动速度向上游,法向速度向上远离壁面,图5是第10尺度扫掠过程脉动速度矢量图,从中可以看出红色框内高速流体向下扫掠的特征。第10尺度流向长度大约相当于5.33倍边界层厚度或1800倍黏性内尺度。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   第10尺度喷射过程脉动速度矢量的空间相位平均

Fig. 4   Contour of fluctuating velocity vector during eject for the tenth-scale


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   第10尺度扫掠过程脉动速度矢量的空间相位平均

Fig. 5   Contour of fluctuating velocity vector during sweep for the tenth-scale


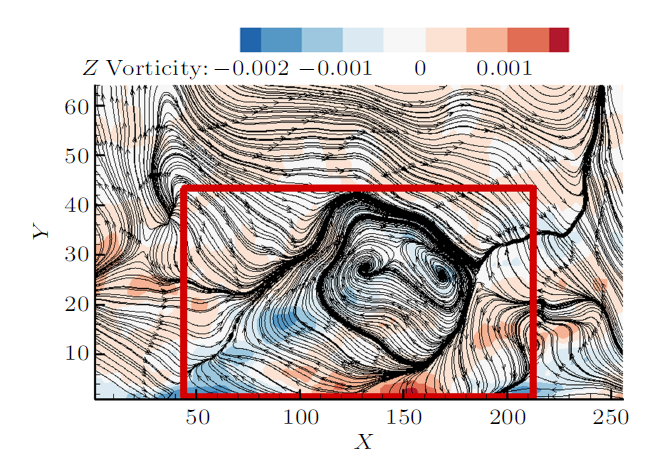
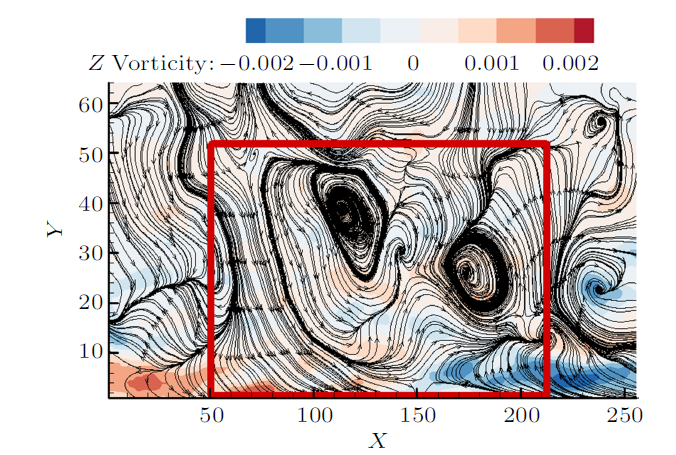
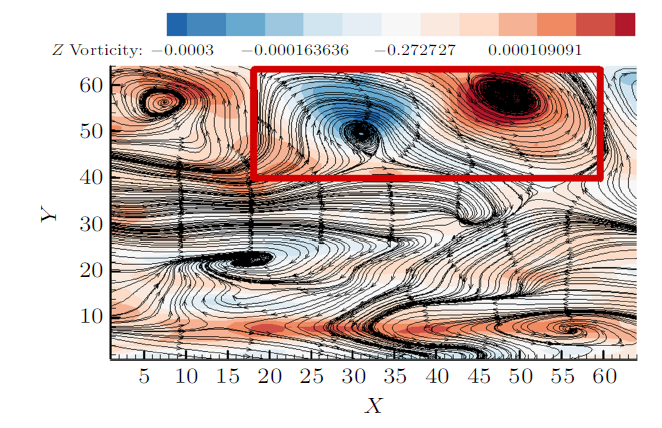
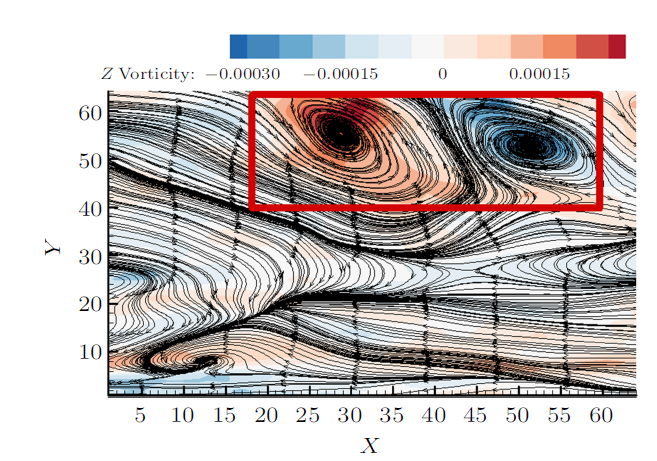
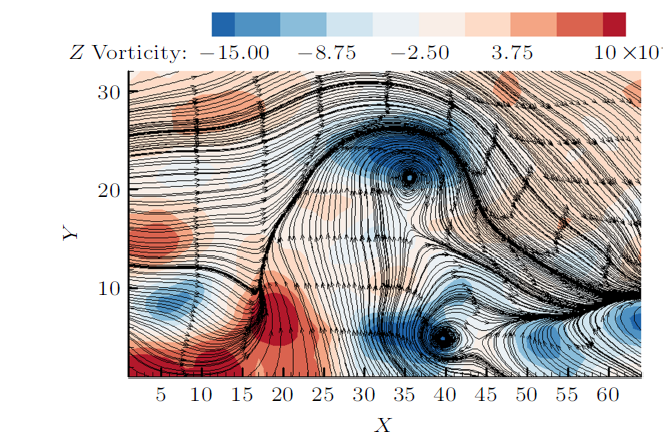
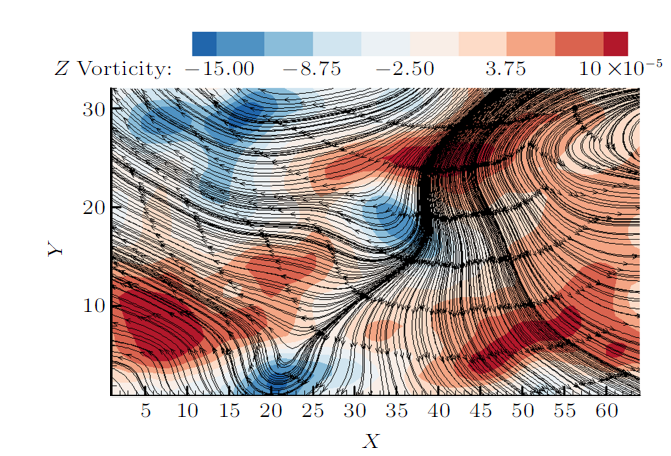
图6为第10尺度喷射事件的空间条件相位平均后的展向涡量云图和流线图,图7为第10尺度扫掠事件的空间条件相位平均后的展向涡量云图和流线图。从图6和图7发现两种大尺度结构都是多个小涡结构组成的复杂大尺度涡包结构,且红色框内大尺度涡包的流线包围了多个小涡结构,小涡位于高速流体和低速流体剧烈剪切的交界处,每个涡结构的流线都是焦点-鞍点组成的不稳定动力系统。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   第10尺度喷射过程展向涡量和流线的空间相位平均

Fig. 6   Contour of the spanwise vorticity and streamlines during eject for the tenth-scale


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   第10尺度扫掠过程展向涡量和流线的空间相位平均

Fig. 7   Contour of the spanwise vorticity and streamlines during sweep for the tenth-scale


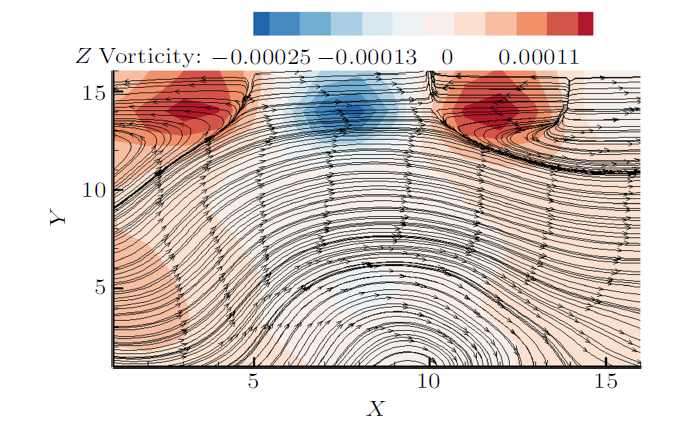
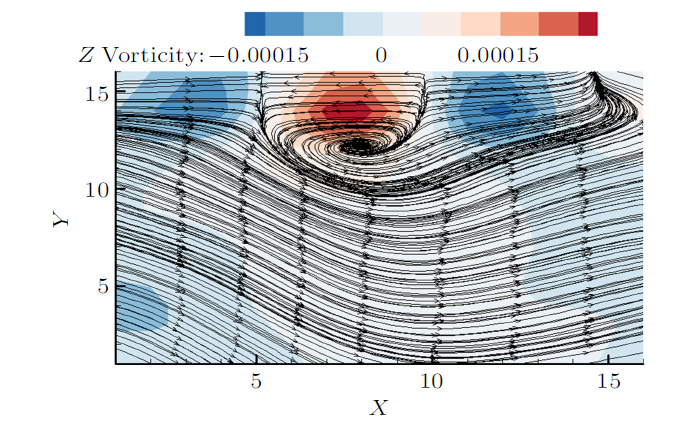
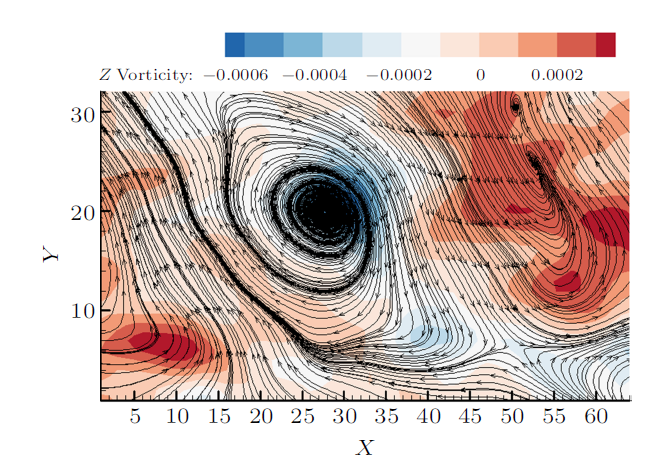
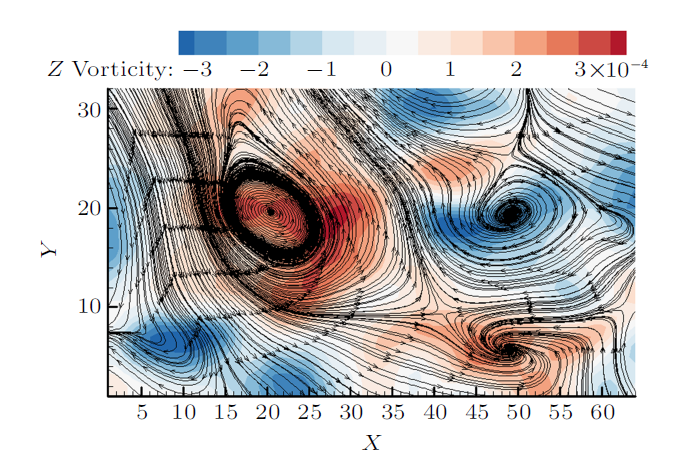
图8和图9为第4尺度位于黏性底层上缘缓冲层附近喷射事件和扫掠事件的空间条件相位平均后的展向涡量云图和流线图。可以看到在黏性底层上缘缓冲层开始处,小尺度涡结构是规则的正负交替的小涡结构,正负小涡之间也是为鞍点结构。图10和图11为第6尺度喷射事件和扫掠事件的空间条件相位平均后的展向涡量云图和流线图,红色框内为一对反向旋转的涡,尺度越大涡略有倾斜,涡的中心是焦点结构,正负小涡之间是鞍点结构。图12和图13为第7尺度喷射事件和扫掠事件的空间条件相位平均后的展向涡量云图和流线图。图14和图15为第8尺度喷射事件和扫掠事件的空间条件相位平均后的展向涡量云图和流线图。发现从第7尺度开始,结构由较小的涡旋结构组合而成。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   第4尺度喷射过程展向涡量和流线的空间相位平均

Fig. 8   Contour of the spanwise vorticity and streamlines during eject for the fourth-scale


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   第4尺度扫掠过程展向涡量和流线的空间相位平均

Fig. 9   Contour of the spanwise vorticity and streamlines during sweep for the fourth-scale


图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   第6尺度喷射过程展向涡量和流线的空间相位平均

Fig. 10   Contour of the spanwise vorticity and streamlines during eject for the sixth-scale


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   第6尺度扫掠过程展向涡量和流线的空间相位平均

Fig. 11   Contour of the spanwise vorticity and streamlines during sweep for the sixth-scale


图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   第7尺度喷射过程展向涡量和流线的空间相位平均

Fig. 12   Contour of the spanwise vorticity and streamlines during eject for the seventh-scale


图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   第7尺度扫掠过程展向涡量和流线的空间相位平均

Fig. 13   Contour of the spanwise vorticity and streamlines during sweep for the seventh-scale


图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   第8尺度喷射过程展向涡量和流线的空间相位平均

Fig. 14   Contour of the spanwise vorticity and streamlines during eject for the eighth-scale


图15

新窗口打开| 下载原图ZIP| 生成PPT

图15   第8尺度扫掠过程展向涡量和流线的空间相位平均

Fig. 15   Contour of the spanwise vorticity and streamlines during sweep for the eighth-scale


基于以上分析,可以发现前6个尺度的结构均是单个涡旋结构,而从第7尺度开始,大尺度结构是由多个小尺度涡旋组成的复杂涡包结构,小涡一般位于高速流体和低速流体剧烈剪切的交界处,每个涡结构的流线都表现为焦点-鞍点组成的不稳定动力系统,大尺度(6尺度以上)的涡结构表现为多个鞍点-焦点局部不稳定动力系统的空间组合。

4 结论

使用四相机阵列得到湍流边界层流法向尺度大小为$6.7\delta \times 1.2\delta$的PIV二维瞬时速度场,用流向脉动速度空间多尺度小波分解的方法得到流向湍动能沿流向尺度和法向坐标的分布,使用条件采样和空间相位平均的方法得到不同尺度相干结构喷射和扫掠的空间拓扑形态,得到以下结论。

(1) 流场中存在着流向能量最大尺度,最大能量所在法向位置为$y^{+}=4.67$,最大湍动能结构的流向空间尺度约相当于5.33倍边界层厚度或1800倍黏性内尺度。随着法向位置远离壁面和流向尺度变大或变小,湍动能逐渐减少。

(2) 前6个尺度的结构是单个涡旋结构,位于高速流体和低速流体交界的高剪切区域,涡结构的流线表现为一个鞍点和焦点组成的局部不稳定结构,两个涡结构之间以鞍点间隔区分。从第7尺度开始,大尺度结构是由多个小尺度涡组成的复杂涡包结构。

参考文献

张兆顺, 崔桂香, 许春晓.

走近湍流

力学与实践, 2002(1): 1-8, 17

[本文引用: 1]

Zhang Zhaoshun, Cui Guixiang, Xu Chunxiao.

Near turbulence

Mechanics in Engineering, 2002(1): 1-8, 17 (in Chinese)

[本文引用: 1]

王振东.

湍流研究的进展

物理通报, 1992(12): 1-4

Wang Zhendong.

Research progress of turbulence

Chinese Physics Bulletin, 1992(12): 1-4 (in Chinese)

Robinson SK.

Coherent motions in the turbulent boundary layer

Annu. Rev. Fluid Mech, 1991, 23(1): 601-639

DOI      URL    

Cantwell BJ.

Organized motion in turbulent flow

Annu. Rev. Fluid Mech, 1981, 13(1): 457-515

DOI      URL    

Hussain AKMF.

Coherent structures and turbulence

J. Fluid Mech, 1986, 173(1): 303-356

DOI      URL     [本文引用: 1]

舒玮, 姜楠.

湍流中涡的尺度分析

空气动力学学报, 2000, 18(S1): 89-95

[本文引用: 1]

Shu Wei, Jiang Nan.

Eddy scale analysis in turbulence

Acta Aero dynamical Sinica, 2000, 18(S1): 89-95 (in Chinese)

[本文引用: 1]

She ZS, Leveque E.

Universal scaling laws in fully developed turbulence

Phys Rev Lett, 1994, 72(3): 336-339

PMID      [本文引用: 1]

Del Lamo JC, Jiménez J, Zandonade P, et al.

Scaling of the energy spectra of turbulent channels

J. Fluid Mech., 1999, 500: 135-144

DOI      URL     [本文引用: 1]

姜楠, 王振东, 舒玮.

分析辨识壁湍流猝发事件的能量最大准则

力学学报, 1997, 29(4): 406-411

DOI      [本文引用: 1]

用子波分析的方法,对用热膜测速仪得到的平板湍流边界层中流向脉动速度信号,在时域空间和频域空间同时进行时频双局部化分解．用子波系数研究了壁湍流脉动动能随尺度的分布,提出了确定壁湍流猝发事件时间尺度参数的能量最大准则,用子波逆变换得到了猝发事件对应的速度信号波形

Jiang Nan, Wang Zhendong, Shu Wei.

The maximum energy criterion for identifying burst events in wall turbulence using wavelet analysis

Chinese Journal of Theoretical and Applied Mechanics, 1997, 29(4): 406-411 (in Chinese)

[本文引用: 1]

Kim KC, Adrian RJ.

Very large-scale motion in the outer layer

Physics of Fluids, 1999, 11(2): 417-422

DOI      URL     [本文引用: 1]

Monty J, Hutchins N, Marusic I, et al.

A comparison of turbulent pipe, channel and boundary layer flows

J. Fluid Mech., 2009, 632: 431-442

DOI      URL     [本文引用: 1]

姜楠, 于培宁, 管新蕾.

湍流边界层相干结构空间拓扑形态的层析TRPIV测量

航空动力学报, 2012, 27(5): 1113-1121

[本文引用: 1]

Jiang Nan, Yu Peining, Guan Xinlei.

Tomographic TRPIV measurement of spatial topological morphology of coherent structures in turbulent boundary layers

Journal of Aerospace Power, 2012, 27(5): 1113-1121 (in Chinese)

[本文引用: 1]

Yang SQ, Jiang N.

Tomographic TR-PIV measurement of coherent structure spatial topology utilizing an improved quadrant splitting method

Science China Physics, Mechanics and Astronomy, 2012, 55(10): 1863-1872

DOI      URL     [本文引用: 1]

Westerweel J, Elsinga GE, Adrian RJ.

Particle image velocimetry for complex and turbulent flows

Annual Review of Fluid Mechanics, 2013, 45: 409-436

DOI      URL     [本文引用: 1]

Adrian RJ, Westerweel J. Particle Image Velocimetry. Cambridge: Cambridge University Press, 2011

Adrian RJ.

Particle image techniques for experimental fluid mechanics

Annu. Rev. Fluid Mech, 1991, 23: 261-304

DOI      URL    

Adrian RJ.

Twenty years of particle image velocimetry

Exp. Fluids, 2005, 39(2): 159-169

DOI      URL     [本文引用: 1]

Farge M.

Wavelet transforms and their applications to turbulence

Annual Review of Fluid Mechanics, 1992, 24: 395-457

DOI      URL     [本文引用: 1]

Farge M, Kevlahan N, Perrier V, et al.

Wavelets and turbulence

Proceedings of the IEEE, 1996, 84(4): 639-669

DOI      URL    

Farge M, Kai S.

Coherent vortex simulation (CVS), a semi-deterministic turbulence model using wavelets

Flow Turbulence and Combustion, 2001, 66(4): 393-426

DOI      URL     [本文引用: 1]

Tennekes H, Lumley JL. A First Course in Turbulence. England: MIT Press Cambridge Massachussetts and London, 1972

[本文引用: 1]

Shen JQ, Pan C, Wang JJ.

Accurate measurement of wall skin friction by single-pixel ensemble correlation

Science China Physics Mechanics & Astronomy, 2014, 57(7): 1352-1362

[本文引用: 1]

樊星, 姜楠.

用平均速度剖面法测量壁湍流摩擦阻力

力学与实践, 2005, 27(1): 28-30

[本文引用: 1]

Fan Xing, Jiang Nan.

Skin friction measurement in turbulent boundary layer by mean velocity profile method

Mechanics in Engineering, 2005, 27(1): 28-30 (in Chinese)

[本文引用: 1]

Spalding DB.

A single formula for the “Law of the Wall”

Transaction of the Asme Journal of Applied Mechanics, 1961, 28(3): 455

DOI      URL     [本文引用: 1]

王康俊, 白建侠, 唐湛棋 等.

用平均速度剖面法测量湍流边界层壁面摩擦速度的对比研究

实验力学, 2019, 34(2): 209-216

[本文引用: 1]

Wang Kangjun, Bai Jianxia, Tang Zhanqi, et al.

Comparative study on the measurement of wall friction velocity of turbulent boundary layer by means of average velocity profile

Journal of experimental mechanics, 2019, 34(2): 209-216 (in Chinese)

[本文引用: 1]

Liu JH, Jiang N, Wang ZD, et al.

Multi-scale coherent structures in turbulent boundary layer detected by locally averaged velocity structure functions

Appl. Math. Mech. (Engl. edn.), 2005, 26(4): 495-504

[本文引用: 1]

Jiang N, Liu W, Liu JH, et al.

Phase-averaged waveforms of Reynolds stress in wall turbulence during the burst events of coherent structures

Science in China Series G-Physics Mechanics & Astronomy, 2008, 51(7): 857-866

[本文引用: 1]

Tian HP, Zhang JX, Wang ED, et al.

Experimental investigation on drag reduction in turbulent boundary layer over superhydrophobic surface by TRPIV

Theoretical Applied Mechanics Letters, 2015, 5(1): 45-49

DOI      URL     [本文引用: 1]

Tian H, Yang S, Cheng L, et al.

Antisymmetric quadrupole mode of coherent structures in wall-bounded turbulence

Theoretical and Applied Mechanics Letters, 2013, 3(5): 52002

DOI      URL     [本文引用: 1]

Tian HP, Jiang N, Huang YX, et al.

Study on local topology model of low/high streak structures in wall-bounded turbulence by tomographic time-resolved particle image velocimetry

Applied Mathematics and Mechanics (English Edition), 2015, 36(8): 1-10

DOI      URL     [本文引用: 1]

/

〈 〉