在工程实践和应用中常见到组合梁,如钢木组合梁、钢混凝土组合梁,工程中常见的组合梁由2$\sim$3种不同材料组成。组合梁的分析对深入理解弯曲及弯曲应力的概念起到加深和巩固的作用。组合梁分析通常是对2种不同材料组成的梁进行分析。全国周培源大学生力学竞赛个人赛题组合梁的分析:第8届第3题顶部增强的悬臂梁是分析2种材料组成的组合梁的中性轴和切应力[1 ] ;第12届第2题分析2种材料组成的三层复合梁的中性层、曲率及弯曲正应力问题。授课时结合赛题进行分析,使学生对组合梁截面的几何性质及弯曲的概念有了新的认识,夯实了学生的基础知识,提高了学生思辩和深入准确理解概念的能力,激发了学生对学习过程中遇到问题思考和讨论的积极性,培养学生逻辑思维和解决问题的能力。
1 中性轴位置确定方法
1.1 相当截面法
相当截面法是将组合梁截面转换为仅由一种材料构成的截面[2 -4 ] 。即保持组合材料的截面高度不变,根据弹性模量确定被转换材料的相当宽度。
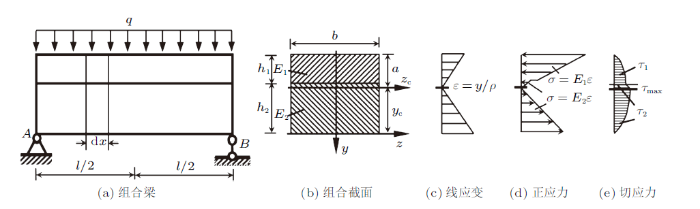
例:图1 矩形截面简支梁承受集度为$q$的均布力,梁由1和2两种材料胶结在一起,已知$E_{1}=2E$, $E_{2}= E$, $b$, $h_{1}= h/2$, $h_{2}= h$, 求中性轴$z$轴位置;分析梁的正应力与切应力。
图1
采用相当截面法,将材料2转换成材料1,则材料2转换成材料1后其相当宽度为
(1) $b_{2} =\frac{E_{2} }{E_{1} }b=0.5b$
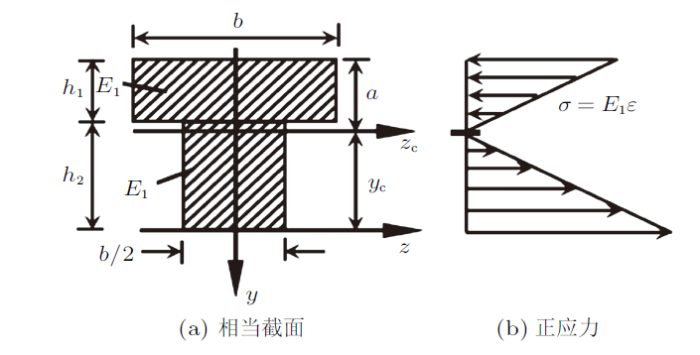
以图2 (a)的$z$轴为参考轴,由组合截面静矩的概念,各截面对$z$轴的静矩等于整个截面对$z$轴的静矩
(2) $Ay_{\rm c} =\sum\limits_{i=1}^2 {A_{i} y_{ci} }$
图2
(3) $y_{\rm c}=7h/8$
1.2 加权平均法
加权平均法是将不同材料的弹性模量作为各自的权重,确定组合梁中性轴位置的方法。将材料的静矩乘其权重弹性模量作为加权后的静矩,将材料的面积乘其权重弹性模量作为加权后的面积。以图1 (b)的$z$轴为参考轴,由组合截面静矩的概念,采用加权平均法,则图1 组合梁中性轴位置为
(4) $y_{\rm c} =\frac{E_{1} S_{Z1} +E_{2} S_{Z2} }{E_{1} A_{1} +E_{2} A_{2} }=\frac{7h}{8}$
式中,$S_{Zi}$为材料$i$对$z$轴的静矩。
组合梁中性轴的位置也可用轴力分析法确定:即梁弯曲时,根据横截面上轴力的合力为零的概念[2 -4 ] 求得。由$F_{\rm N}=0$,可得$a=5h/8$,$a$与$y_{\rm c}$之和等于截面的高度1.5$h$。
相当截面法和加权平均法确定中性轴位置:是以组合梁的上底边或下底边为参考轴,依据相当和加权的概念确定中性轴的位置,与轴力分析法相比算式简洁、计算简便,其中加权平均法最为简单。相当截面法可演化为加权平均法,两种方法均可以求多种不同材料组合梁的中性轴位置。加权平均法求$n$种不同材料组合梁的中性轴位置计算公式为
(5) $y=\frac{\sum\limits_{i=1}^n {E_{i} } S_{Zi} }{\sum\limits_{i=1}^n {E_{i} A_{i} } }$
2 应力分析
2.1 正应力分析
弯曲梁的线应变$\varepsilon $与$y$和曲率半径$\rho$有关,组合梁截面的线应变是协调的,见图1 (c);梁的正应力与弹性模量$E$和线应变$\varepsilon$有关,组合梁横截面上的正应力因材料性质差异在结合处将发生突变[2 ,5 ] ,见图1 (d)。依平面假设,梁弯曲时横截面似刚性平面绕中性轴转动了一个角度,转动后依然保持为平面。线应变只有是$y$的线性函数,平面假设才能成立。梁弯曲时材料遵从胡克定律,因此在异质材料结合面上,正应力发生突变。
在组合梁的分析与思考讨论中,采用相当截面法分析组合梁正应力时,同学会出现图2 (b)的问题。其原因是将不同的材料转换成同一材料后,同学将组合梁习惯性地看作是同一材料的梁得出的。采用加权平均法分析时,可避免此种情况的发生。在组合梁的研讨过程中,教师应启发引导学生,学生经过思考推理得出正确结论,这一过程往往促使学生进一步思考问题,从而加深对不同材料组合梁概念的正确理解。
(6) $\sigma_{1}=E_{1}\varepsilon = E_{1} \frac{y}{\rho },\ \sigma_{2} =E_{2}\varepsilon =E_{2} \frac{y}{\rho}$
(7) $\frac{1}{\rho }=\frac{M_{Z} }{E_{1} I_{Z1} +E_{2} I_{Z2} }$
式中,$I_{Zi}$为材料$i$对中性轴$z_{\rm c}$轴的惯性矩。
根据式(6)和式(7)可计算出图1 组合截面上各组成部分任一点的线应变与正应力值。梁的最大曲率发生在简支梁的跨中,梁跨中弯矩值为$ql^{2}/8$。
2.2 切应力分析
根据力的平衡分析,材料1、材料2在d$x$微段梁上(图1 (a))正应力的差值将由界面上的切应力平衡。两种材料的弯曲切应力分别为
(8) $\tau_{1}=\frac{k_{1}F_{{\rm s}} S_{Z1}^{\ast } }{I_{Z} b},\ \tau_{2} =\frac{k_{2} F_{{\rm s}} S_{Z2}^{\ast } }{I_{Z} b}$
(9) ${{I}_{Z}}=({{E}_{1}}{{I}_{Z1}}+{{E}_{2}}{{I}_{Z2}})/{{E}_{1}}$
$S_{Zi}^{\ast } $为材料$i$所求应力的点横线以外的所有面积对中性轴$z_{\rm c}$轴的静矩。$k_{i}$为材料$i$的弹性模量与材料1的弹性模量之比。
在梁的左半段截取d$x$微段(图1 (a))研究异质材料界面处的切应力,根据切应力互等定理,无论由何种材料求界面上的切应力,得到的切应力值必然相等。依据式(8)和式(9)由两种材料分别求界面上的切应力,若
(10) $k_{1} S_{Z1}^{\ast } =k_{2} S_{Z2}^{\ast }$
则在界面上$\tau_{1}$与$\tau_{2}$相等。
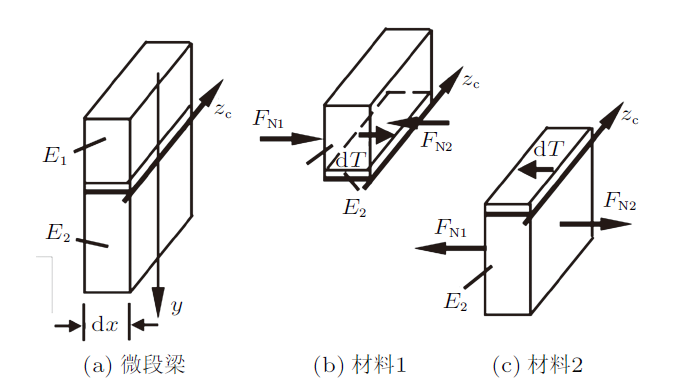
由图1 (b)与图3 (b)材料1对中性轴$z_{\rm c}$轴静矩,得
(11) $k_{1} S_{Z1}^{\ast } =S_{Z1}^{\ast } =bh_{1} \left(\frac{h_{1} }{2}+a-h_{1}\right)=\frac{3bh^{2}}{16}$
图3
由图1 (b)与图3 (c)材料2对中性轴$z_{\rm c}$轴静矩,得
(12) $k_{2} S_{Z2}^{\ast } =0.5S_{Z2}^{\ast } =0.5bh_{2} \left(y_{0} -\frac{h_{2} }{2}\right)=\frac{3bh^{2}}{16}$
现在分析异质界面上切应力的方向,图3 (b)所示的材料1块体位于中性轴$z_{\rm c}$轴上方,材料1是受压的,由于$F_{\rm N2}>F_{\rm N1}$,因此界面上切应力的合力d$T$指向d$x$微段右侧横截面;图3 (c)所示的材料2块体,中性轴$z$轴上方部分受压,下方部分受拉,但因$z$轴下方材料高度大于$z$轴上方材料高度,材料2总体是受拉的,由于$F_{\rm N2}>F_{\rm N1}$,因此界面上切应力的合力d$T$指向d$x$微段左侧横截面。根据切应力互等定理,由图3 (b)与图3 (c)都可得到两块体右侧横截面上的切应力与$y$轴同向且平行,且与梁的切力方向一致。组合梁截面上的最大切应力可据式(8)计算获得。梁截面上的切应力分布见图1 (e)。
3 组合梁附加分析
例:若图1 梁由3种不同材料组合在一起,已知$E_{2}= k_{2}E_{1}=1.5E_{1}$,$E_{3}=k_{3}E_{1}=2E_{1}$,$b$,$h_{1}= h_{2}= h$,$h_{3}=2h$,求中性轴$z_{\rm c}$轴位置,分析梁的正应力与切应力。
相当截面法:将材料2和3均转换成材料1后其相当宽度为
(13) $b_{2}=k_{2}b,\ b_{3}=k_{3}b$
(14) $y_{\rm c}=45h/26$
图4
加权平均法:将不同材料的弹性模量作为各自的权重,由图4 (a)得
(15) $y_{\rm c} =\frac{E_{1} S_{Z1} +E_{2} S_{Z2} +E_{3} S_{Z3} }{E_{1} A_{1} +E_{2} A_{2} +E_{3} A_{3} }=\frac{45h}{26}$
依据轴力分析法可求得$a=59h/26$。则$a+y=h_{1} +h_{2} +h_{3}=4h$验证了中性轴$z_{\rm c}$轴的正确位置。组合梁对中性轴$z_{\rm c}$轴的惯性矩为
(16) $I_{Z} =\sum\limits_{i=1}^n {E_{i} I_{Zi} }$
组合梁的线应变、正应力及切应力分析结果见图4 (b)$\sim$图4 (d)。三种材料的弯曲正应力分别为
(17) $\sigma_{1} =E_{1} \varepsilon,\ \sigma_{2} =E_{2} \varepsilon,\ \sigma_{3}=E_{3} \varepsilon$
(18) $\frac{1}{\rho }=\frac{M_{Z} }{E_{1} I_{Z1} +E_{2} I_{Z2} +E_{3}I_{Z3} }$
(19) $\left.\begin{array}{rl}\tau_{1} & =\frac{k_{1} F_{\mathrm{s}} S_{Z 1}^{*}}{I_{Z} b} \\ \tau_{2} & =\frac{k_{1} F_{\mathrm{s}} S_{Z 1}+k_{2} F_{\mathrm{s}} S_{Z 2}^{*}}{I_{Z} b} \\ \tau_{3} & =\frac{k_{3} F_{\mathrm{s}} S_{Z 3}^{*}}{I_{Z} b}\end{array}\right\}$
(20) ${{I}_{Z}}=({{E}_{1}}{{I}_{Z1}}+{{E}_{2}}{{I}_{Z2}}+{{E}_{3}}{{I}_{Z3}})/{{E}_{1}}$
4 结论
采用相当截面法与加权平均法对2种材料组合梁中性轴的位置、正应力与切应力进行了分析,并对3种材料组合梁进行了附加分析。其中加权平均法使组合梁的分析更加简化。本文的方法可用于工程中常见组合梁的分析。在组合梁的分析讨论中,可引导学生一步一步地展开分析,并且在这一过程中加深对弯曲与截面几何性质之间关系的深入理解,准确理解相关概念,为今后的工程应用打好基础。
参考文献
View Option
[1]
高云峰 , 将持平 . 全国周培源大学生力学竞赛赛题详解及点评 . 北京 : 机械工业出版社 , 2015
[本文引用: 1]
Gao Yunfeng Jiang Chiping . Detailed Explanations and Comments of Questions of the National Zhou Peiyuan College Student Mechanics Competition. Beijing : Machinery Industry Press , 2015 (in Chinese)
[本文引用: 1]
[2]
铁摩辛柯 , 盖尔 J 。 材料力学. 胡人礼译 . 北京 : 科学出版社 , 1978
[本文引用: 3]
Timoshenko S Gere J . Mechanics of Materials. Hu Renli Transl. Beijing : Science Press , 1978 (in Chinese)
[本文引用: 3]
[3]
孙训方 , 方孝淑 , 关来泰 . 材料力学(II) . 北京 : 高等教育出版社 , 2009
Sun Xunfang Fang Xiaoshu Guan Laitai . Mechanics of Materials (II). Beijing : Higher Education Press , 2009 (in Chinese)
[4]
李秀莲 . 等效截面法求解异质双材料组合梁
青海大学学报(自然科学版) , 2008 , 26 (6 ): 93 -96
[本文引用: 2]
[5]
周乾 , 闫维明 . 古建筑木结构叠合梁与组合梁弯曲受力研究
建筑结构 , 2012 , 42 (4 ): 157 -161
[本文引用: 1]
Zhou Qian Yan Weiming . Bending analysis on composite beam and combination beam of Chinese ancient wooden buildings
Building Structure 2012 , 42 (4 ): 157 -161 (in Chinese)
[本文引用: 1]
[6]
唐晓雯 , 尚新春 . 层合梁弯曲正应力的测试与计算
力学与实践 , 2010 , 32 (4 ): 77 -79
[本文引用: 1]
1
2015
... 在工程实践和应用中常见到组合梁,如钢木组合梁、钢混凝土组合梁,工程中常见的组合梁由2$\sim$3种不同材料组成.组合梁的分析对深入理解弯曲及弯曲应力的概念起到加深和巩固的作用.组合梁分析通常是对2种不同材料组成的梁进行分析.全国周培源大学生力学竞赛个人赛题组合梁的分析:第8届第3题顶部增强的悬臂梁是分析2种材料组成的组合梁的中性轴和切应力[1 ] ;第12届第2题分析2种材料组成的三层复合梁的中性层、曲率及弯曲正应力问题.授课时结合赛题进行分析,使学生对组合梁截面的几何性质及弯曲的概念有了新的认识,夯实了学生的基础知识,提高了学生思辩和深入准确理解概念的能力,激发了学生对学习过程中遇到问题思考和讨论的积极性,培养学生逻辑思维和解决问题的能力. ...
1
2015
... 在工程实践和应用中常见到组合梁,如钢木组合梁、钢混凝土组合梁,工程中常见的组合梁由2$\sim$3种不同材料组成.组合梁的分析对深入理解弯曲及弯曲应力的概念起到加深和巩固的作用.组合梁分析通常是对2种不同材料组成的梁进行分析.全国周培源大学生力学竞赛个人赛题组合梁的分析:第8届第3题顶部增强的悬臂梁是分析2种材料组成的组合梁的中性轴和切应力[1 ] ;第12届第2题分析2种材料组成的三层复合梁的中性层、曲率及弯曲正应力问题.授课时结合赛题进行分析,使学生对组合梁截面的几何性质及弯曲的概念有了新的认识,夯实了学生的基础知识,提高了学生思辩和深入准确理解概念的能力,激发了学生对学习过程中遇到问题思考和讨论的积极性,培养学生逻辑思维和解决问题的能力. ...
3
1978
... 相当截面法是将组合梁截面转换为仅由一种材料构成的截面[2 -4 ] .即保持组合材料的截面高度不变,根据弹性模量确定被转换材料的相当宽度. ...
... 组合梁中性轴的位置也可用轴力分析法确定:即梁弯曲时,根据横截面上轴力的合力为零的概念[2 -4 ] 求得.由$F_{\rm N}=0$,可得$a=5h/8$,$a$与$y_{\rm c}$之和等于截面的高度1.5$h$. ...
... 弯曲梁的线应变$\varepsilon $与$y$和曲率半径$\rho$有关,组合梁截面的线应变是协调的,见图1 (c);梁的正应力与弹性模量$E$和线应变$\varepsilon$有关,组合梁横截面上的正应力因材料性质差异在结合处将发生突变[2 ,5 ] ,见图1 (d).依平面假设,梁弯曲时横截面似刚性平面绕中性轴转动了一个角度,转动后依然保持为平面.线应变只有是$y$的线性函数,平面假设才能成立.梁弯曲时材料遵从胡克定律,因此在异质材料结合面上,正应力发生突变. ...
3
1978
... 相当截面法是将组合梁截面转换为仅由一种材料构成的截面[2 -4 ] .即保持组合材料的截面高度不变,根据弹性模量确定被转换材料的相当宽度. ...
... 组合梁中性轴的位置也可用轴力分析法确定:即梁弯曲时,根据横截面上轴力的合力为零的概念[2 -4 ] 求得.由$F_{\rm N}=0$,可得$a=5h/8$,$a$与$y_{\rm c}$之和等于截面的高度1.5$h$. ...
... 弯曲梁的线应变$\varepsilon $与$y$和曲率半径$\rho$有关,组合梁截面的线应变是协调的,见图1 (c);梁的正应力与弹性模量$E$和线应变$\varepsilon$有关,组合梁横截面上的正应力因材料性质差异在结合处将发生突变[2 ,5 ] ,见图1 (d).依平面假设,梁弯曲时横截面似刚性平面绕中性轴转动了一个角度,转动后依然保持为平面.线应变只有是$y$的线性函数,平面假设才能成立.梁弯曲时材料遵从胡克定律,因此在异质材料结合面上,正应力发生突变. ...
等效截面法求解异质双材料组合梁
2
2008
... 相当截面法是将组合梁截面转换为仅由一种材料构成的截面[2 -4 ] .即保持组合材料的截面高度不变,根据弹性模量确定被转换材料的相当宽度. ...
... 组合梁中性轴的位置也可用轴力分析法确定:即梁弯曲时,根据横截面上轴力的合力为零的概念[2 -4 ] 求得.由$F_{\rm N}=0$,可得$a=5h/8$,$a$与$y_{\rm c}$之和等于截面的高度1.5$h$. ...
古建筑木结构叠合梁与组合梁弯曲受力研究
1
2012
... 弯曲梁的线应变$\varepsilon $与$y$和曲率半径$\rho$有关,组合梁截面的线应变是协调的,见图1 (c);梁的正应力与弹性模量$E$和线应变$\varepsilon$有关,组合梁横截面上的正应力因材料性质差异在结合处将发生突变[2 ,5 ] ,见图1 (d).依平面假设,梁弯曲时横截面似刚性平面绕中性轴转动了一个角度,转动后依然保持为平面.线应变只有是$y$的线性函数,平面假设才能成立.梁弯曲时材料遵从胡克定律,因此在异质材料结合面上,正应力发生突变. ...
古建筑木结构叠合梁与组合梁弯曲受力研究
1
2012
... 弯曲梁的线应变$\varepsilon $与$y$和曲率半径$\rho$有关,组合梁截面的线应变是协调的,见图1 (c);梁的正应力与弹性模量$E$和线应变$\varepsilon$有关,组合梁横截面上的正应力因材料性质差异在结合处将发生突变[2 ,5 ] ,见图1 (d).依平面假设,梁弯曲时横截面似刚性平面绕中性轴转动了一个角度,转动后依然保持为平面.线应变只有是$y$的线性函数,平面假设才能成立.梁弯曲时材料遵从胡克定律,因此在异质材料结合面上,正应力发生突变. ...