力学与实践, 2021, 43(6): 964-966 DOI: 10.6052/1000-0879-21-019

教育研究

从受拉杆变形浅析弹性力学中的最小势能原理

吴枝根,1), 李孝宝, 孟增, 詹春晓

合肥工业大学土木与水利工程学院,合肥 230009

ON PRINCIPLE OF MINIMUM POTENTIAL ENERGY IN ELASTICITY FROM DEFORMATION OF BARS SUBJECTED TO TENSION

WU Zhigen,1), LI Xiaobao, MENG Zeng, ZHAN Chunxiao

School of Civil Engineering, Hefei University of Technology, Hefei 230009, China

通讯作者: 1)吴枝根,教授,研究方向为复合材料力学和软物质力学。E-mail:zhigenwu@hfut.edu.cn

责任编辑: 胡漫

收稿日期: 2021-01-12   修回日期: 2021-03-12  

Received: 2021-01-12   Revised: 2021-03-12  

作者简介 About authors

摘要

最小势能原理是弹性力学中较难理解的知识点。本文通过对弹性杆轴向受拉时的弹性势能、外力势能和总势能的变分分析,得出总势能变分是位移变分或应变变分的二阶无穷小量,并在位移变分或应变变分为零时,总势能取得极小值。弹性杆轴向受力变形的分析应验了最小势能原理,有助于对一般情况下最小势能原理的深刻理解。

关键词： 弹性力学; 最小势能原理; 弹性变形; 虚位移

Abstract

The principle of minimum potential energy in elasticity is comparatively difficult to understand. In this paper, by variational analyses on elastic potential energy, external force potential energy and total potential energy of elastic bars subjected to tension, it is obtained that the variation of total potential energy is the second order infinitesimal of the displacement variation or strain variation. Furthermore, when the displacement variation or strain variation equals to zero, the total potential energy reaches the minimum. The principle of minimum potential energy is thereby examined by the analysis of deformation for elastic bars under axial forces, which is helpful to profoundly understand the principle of minimum potential energy in general.

Keywords： elasticity; principle of minimum potential energy; elastic deformation; virtual displacement

PDF (133KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

吴枝根, 李孝宝, 孟增, 詹春晓. 从受拉杆变形浅析弹性力学中的最小势能原理. 力学与实践, 2021, 43(6): 964-966 DOI:10.6052/1000-0879-21-019

WU Zhigen, LI Xiaobao, MENG Zeng, ZHAN Chunxiao. ON PRINCIPLE OF MINIMUM POTENTIAL ENERGY IN ELASTICITY FROM DEFORMATION OF BARS SUBJECTED TO TENSION. Mechanics in Engineering, 2021, 43(6): 964-966 DOI:10.6052/1000-0879-21-019

最小势能原理是弹性力学教学中的重点,也是难点。很多教材中,公式推导过程都相当严密,例如：文献[1]在给出总势能的一阶变分等于0的情况下,进而提出二阶变分大于0,可证明总势能在实际存在的一组位移中取得极小值;文献[2]推导了几何可能位移场的总势能总是大于真实位移场的总势能,用到了应变能密度为正定函数的性质;文献[3]认为只要应变能函数是凸函数,则由凸函数的性质得出一切可能的变形中,真实变形的总势能最小。客观地说,由于问题的复杂性,要想清晰地理解这一原理对于初学者还是有一定的难度。本文从轴向受拉杆的变形出发,简单而直观地揭示最小势能原理所蕴含的机理。

1 线弹性杆的变形分析

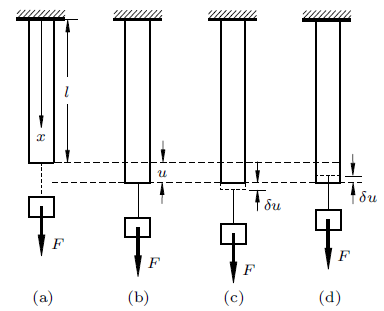
如图1(a)所示,弹性杆上端固定,下端自由,杆的长度为$l$,横截面面积为$A$,弹性模量为$E$。当杆的下端悬挂重量为$F$的重物时,下端向下产生位移$u$ (图1(b)),故弹性杆的弹性势能为

$\begin{eqnarray} V_{{\rm e}} =\frac{1}{2}ku^{2} \end{eqnarray}$

式中$k={EA}/{l}$。重物的重力势能,即弹性杆上作用的外力势能为

$\begin{eqnarray} V_{{\rm p}} =-Fu \end{eqnarray}$

系统的总势能为$V_{{\rm e}} +V_{{\rm p}} $。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   弹性杆及其受重物作用后的变形和虚位移


现假定弹性杆的下端沿$x$方向有一个增量,即一个虚位移或位移变分$\delta u$ (图1(c)和图1(d)),则弹性势能也随之有一个变分$\delta V_{{\rm e}} $,且

$\begin{eqnarray} \delta V_{{\rm e}} =\frac{1}{2}k(u+\delta u)^{2}-\frac{1}{2}ku^{2}=ku\delta u+\frac{1}{2}k(\delta u)^{2} \end{eqnarray}$

外力势能的变分

$\begin{eqnarray} \delta V_{{\rm p}} =-F(u+\delta u)+Fu=-F\delta u \end{eqnarray}$

总势能的变分

$\begin{eqnarray} \delta (V_{{\rm e}} +V_{{\rm p}} )=ku\delta u+\frac{1}{2}k(\delta u)^{2}-F\delta u \end{eqnarray}$

考虑到线弹性杆有$F=ku$,于是

$\begin{eqnarray} \delta (V_{{\rm e}} +V_{{\rm p}} )=\frac{1}{2}k(\delta u)^{2} \end{eqnarray}$

由此可见,总势能的变分$\delta (V_{{\rm e}} +V_{{\rm p}})$是位移变分$\delta u$的二阶无穷小量,当$\delta u\to 0$时,$\delta (V_{{\rm e}} +V_{{\rm p}})$的极限等于0,当且仅当$\delta u=0$时总势能变分取得极小值,并等于0。因为$\delta u=0$对应于实际存在的位移,所以在给定的外力作用下,实际存在的位移使总势能取得极小值,即最小势能原理。

2 非线弹性杆的变形分析

设加载过程中,非线弹性杆下端受到的拉力$f$与下端的位移$u_{f}$的关系为

$\begin{eqnarray} f=f(u_{f} ) \end{eqnarray}$

则非线弹性杆的弹性势能

$\begin{eqnarray} V_{{\rm e}} =\int_0^u {f(u_{f} )} {\rm d}u_{f} \end{eqnarray}$

由位移变分引起的弹性势能变分

$\begin{eqnarray} &&\delta V_{{\rm e}} =\int_0^{u+\delta u} {f(u_{f} )}{\rm d}u_{f} -\int_0^u {f(u_{f} )} {\rm d}u_{f} =\\&&\qquad \int_u^{u+\delta u} {f(u_{f} )} {\rm d}u_{f} \end{eqnarray}$

由于在弹性范围内,外力$f$总是关于位移$u_{f}$的连续且单调增函数,由积分中值定理可得

$\begin{eqnarray} \int_u^{u+\delta u} {f(u_{f} )} {\rm d}u_{f} =f(\xi )\delta u \end{eqnarray}$

式中

$u<\xi <u+\delta u\ (\delta u>0)$

或

$u+\delta u<\xi <u\ (\delta u<0)$

非线弹性杆外力势能的变分仍然是式(4),这时$F=f(u)$,于是总势能变分

$\begin{eqnarray} &&\delta(V_{{\rm e}} +V_{{\rm p}} )=f(\xi )\delta u-f(u)\delta u=\\&&\qquad [f(\xi )-f(u)]\delta u \end{eqnarray}$

考虑到弹性范围内外力是关于位移的增函数,当$\delta u>0$时,有$\xi>u$和$f(\xi )-f(u)>0$;当$\delta u<0$时,有$\xi <u$和$f(\xi)-f(u)<0$。因此,式(11)等号右边$f(\xi )-f(u)$与$\delta u$两项总保持相同的正负号,其乘积必大于0,当且仅当$\delta u=0$时其乘积等于零。总势能变分$\delta(V_{{\rm e}} +V_{{\rm p}})$是位移变分$\delta u$的二阶无穷小量,且在位移变分为零时取得极小值,因此对非线弹性杆的变形分析同样有最小势能原理。

3 基于线弹性应变能的分析

如果考虑弹性受拉杆自身重力,即沿$x$方向的体力$\rho g$,这时沿$x$方向的线应变$\varepsilon_{x}$是关于$x$的函数。对于线弹性情况,弹性杆的应变能

$\begin{eqnarray} V_{\varepsilon } =\frac{1}{2}E\int_V {\varepsilon_{x}^{2} {\rm d}V} \end{eqnarray}$

应变能的变分

$\begin{eqnarray} &&\delta V_{\varepsilon } =\frac{1}{2}E\int_V {[(\varepsilon_{x} +\delta \varepsilon_{x} )^{2}-\varepsilon_{x}^{2} ]{\rm d}V} =\\&&\qquad E\int_V {\varepsilon_{x} \delta \varepsilon_{x} {\rm d}V+} \frac{1}{2}E\int_V {(\delta \varepsilon_{x} )^{2}{\rm d}V} =\\&&\qquad\int_V {\sigma_{x} \delta \varepsilon_{x} {\rm d}V} +\frac{1}{2}E\int_V {(\delta \varepsilon_{x} )^{2}{\rm d}V} \end{eqnarray}$

式中$\sigma_{x}$表示弹性杆横截面上的正应力。弹性杆在体力和拉力作用下,外力势能的变分为

$\begin{eqnarray} \delta V_{{\rm p}} =-F\delta u-\int_V {\rho g} \delta u_{x} {\rm d}V \end{eqnarray}$

式中$\delta u_{x}$表示与杆下端位移变分$\delta u$对应的$x$截面的位移变分。

根据虚位移原理,即：如果在虚位移发生之前,弹性体是处于平衡状态,那么在虚位移过程中,外力在虚位移上所做的虚功就等于应力在与该虚位移相应的虚应变上所做的虚功[1],有

$\begin{eqnarray} F\delta u+\int_V {\rho g} \delta u_{x} {\rm d}V=\int_V{\sigma_{x} } \delta \varepsilon_{x} {\rm d}V \end{eqnarray}$

由式(13)~式(15)可得总势能变分

$\begin{eqnarray} \delta(V_{\varepsilon } +V_{{\rm p}} )=\frac{1}{2}E\int_V{(\delta \varepsilon_{x} )^{2}{\rm d}V} \end{eqnarray}$

因此,在考虑体力和面力的情况下,弹性杆总势能变分是应变变分的二阶无穷小量,在应变变分为零时总势能取得极小值,即为最小势能原理。

4 结束语

(1)通过给出弹性杆在轴向受拉情况下的弹性势能和外力势能以及它们的变分和总势能变分的准确形式,得出：无论是线性还是非线性,其总势能变分都是位移变分或应变变分的二阶无穷小量,只有在位移变分或应变变分等于零时总势能变分才取得极小值,均应验了最小势能原理。

(2)计算外力势能时外力是一个恒定的量,文中采用物体的重力作为外力,将重力势能作为外力势能,便于形成外力势能的概念,避免产生外力随物体变形而改变的思维习惯。

(3)虽然从弹性杆的轴向受力变形解释了最小势能原理,对于一般情况下的最小势能原理具有相同实质,有助于理解最小势能原理的真实含义。

参考文献

徐芝纶. 弹性力学(上册), 第5版. 北京: 高等教育出版社, 2016

[本文引用: 2]

Xu Zhilun. Elasticity (I), 5th edn. Beijing: Higher Education Press, 2016 (in Chinese)

[本文引用: 2]

吴家龙. 弹性力学, 第3版. 北京: 高等教育出版社, 2016

[本文引用: 1]

Wu Jialong. Elasticity, 3rd edn. Beijing: Higher Education Press, 2016 (in Chinese)

[本文引用: 1]

陆明万, 罗学富. 弹性理论基础(下册), 第2版. 北京: 清华大学出版社, 2001

[本文引用: 1]

Lu Mingwan, Luo Xuefu. Foundations of Elasticity (II), 2nd edn. Beijing: Tsinghua University Press, 2001 (in Chinese)

[本文引用: 1]

/

〈 〉