蒸汽管网的动力学建模与迭代方法$^{1)}$

doi:10.6052/1000-0879-21-160

蒸汽管网的动力学建模与迭代方法$^{1)}$

王安然^*, 曾波^†, 张勍^†, 杨荣超^†, 张凯^,^*^,²⁾, 赵瑶^*, 张明^**, 赵晓东^*, 宿彬^*, 李祎萍^*, 张鹏飞^†

^*中国计量大学计量测试工程学院,杭州 310018

^†郑州烟草研究院中国烟草标准化研究中心,郑州 450001

^**国家电投集团河南电力有限公司,郑州 450018

DYNAMIC MODELING AND ITERATIVE METHOD OF STEAM PIPE NETWORK$^{1)}$

WANG Anran^*, ZENG Bo^†, ZHANG Qing^†, YANG Rongchao^†, ZHANG Kai^,^*^,²⁾, ZHAO Yao^*, ZHANG Ming^**, ZHAO Xiaodong^*, SU Bin^*, LI Yiping^*, ZHANG Pengfei^†

^*College of Metrology & Measurement Engineering, China Jiliang University, Hangzhou 310018, China

^†China Tobacco Standardization Research Center, Zhengzhou Tobacco Research Institute, Zhengzhou 450001, China

^**Henan Electric Power Co., Ltd., State Power Investment Corporation, Zhengzhou 450018, China

通讯作者: 2)张凯,教授,主要从事流体的传热、传质研究。E-mail:zkzb3026@gmail.com

责任编辑: 胡漫

收稿日期: 2021-04-19 修回日期: 2021-07-19

基金资助:

1)国家自然科学基金资助项目(11472260)

Received: 2021-04-19 Revised: 2021-07-19

作者简介 About authors

摘要

热电联产过程中的蒸汽输送过程难以监测,流量和压力变化比较复杂,管网运维依赖人员经验,容易造成能源浪费。本文建立了蒸汽供热管网的动态仿真模型,模型将蒸汽管网假设为单相可压缩流体网络,由节点和管路组成。使用管网质量方程、动量方程和能量方程建立管网物理模型,并采用隐式欧拉算法、稀疏矩阵算法求解由物理模型所得的非线性微分方程组。此外,本文建立了简单管网,并结合Fluent仿真对算法进行了验证。最后,建立了实际管网模型,与某企业蒸汽管网实际运行数据进行对比,结果表明所提出的模型不仅具有计算准确性,而且有实际工程应用价值。

关键词： 蒸汽管网; 动态仿真; 网络拓扑; 算法研究

Abstract

In the process of cogeneration of heat and power, many factors affect the energy efficiency, such as the difficulty to monitor the steam transmission process, the complex change of flow rate and pressure, and the requirement of experience of personnel for the operation and maintenance of pipe network. This paper develops a dynamic simulation model of steam heating pipe network. The model presumes a single-phase compressible steam pipe network composed of nodes and pipelines. The mass equation, momentum equation and energy equation of the pipe network are used to establish the physical model of the pipe network. The implicit Euler algorithm and sparse matrix algorithm are used to solve the nonlinear differential equations obtained from the physical model. In addition, this paper constructed a simple pipe network as an example, and numerical simulation with Fluent was carried out to verify the algorithm. Finally, the actual pipe network model is established and compared with the actual operation data of a steam pipe network in an enterprise. The results show that the proposed model is not only accurate in calculation, but also valuable in practical engineering application.

Keywords： steam pipe network; dynamic simulation; network topology; algorithm research

PDF (2053KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王安然, 曾波, 张勍, 杨荣超, 张凯, 赵瑶, 张明, 赵晓东, 宿彬, 李祎萍, 张鹏飞. 蒸汽管网的动力学建模与迭代方法$^{1)}$. 力学与实践, 2021, 43(6): 905-913 DOI:10.6052/1000-0879-21-160

WANG Anran, ZENG Bo, ZHANG Qing, YANG Rongchao, ZHANG Kai, ZHAO Yao, ZHANG Ming, ZHAO Xiaodong, SU Bin, LI Yiping, ZHANG Pengfei. DYNAMIC MODELING AND ITERATIVE METHOD OF STEAM PIPE NETWORK$^{1)}$. Mechanics in Engineering, 2021, 43(6): 905-913 DOI:10.6052/1000-0879-21-160

目前,热蒸汽作为热电联产生产中重要的传输介质,在蒸汽输送过程中状态参数变化大,伴随有相变过程,具体的网络计算方法涉及到传热学、流体力学方面的问题。目前对管网的设计和运行调节计算较为简单^[1-3],水力计算主要靠人工查取水力计算图进行近似计算,热力计算甚至有时假设忽略,未考虑蒸汽的可压缩性和物性改变,这给蒸汽管网的计算带来了较大误差。

对蒸汽管道中的流量进行计量是一个复杂的课题^[4-5],流体管网计算涉及到几个基本方程：质量守恒、动量守恒和能量守恒^[6],运用这三个方程可以构建基础流体管网模型^[7-8]。目前该领域的研究较少,且集中在地热蒸汽管道的应用方面^[9-10]。计算蒸汽管网首先需要建立蒸汽管网模型和模拟蒸汽管网结构,管网主体是节点与管道^[11-13]。

现在,存在软件程序如PIPEPHASE和SIMSNET等,可以对流体管网进行数值模拟^[14],在管道网络构建及改造过程中能发挥重大作用^[15-16],但多用于石油化工等领域。在处理蒸汽管网过程中,会存在很多问题,例如存在排水损失的问题,Wang等^[17]研究了适用于排水损失的热力模型,考虑了管网内冷凝水的影响,证明了疏水损失对蒸汽温度和密度沿管道的分布有显著影响。王雅峰等^[18]研究了二回路的两相流问题,将混合相认为是两个单相,提出了两相流的网络建模方法,计算结果与Jtopmeret软件进行了对比,证明了算法的有效性。Cazarez-Candia等^[19]研究了两相低压多组分的数学模型,该模型将气相和液相(油和水)视为伪单相(混合物),建立的均相模型可以很容易地应用于计算气-液两相流中的压降、混合物温度和混合物速度,模型预测结果与现场数据吻合。

算法研究方面,Desideri等^[20]描述了一种用于通过输入和输出条件(由压力流量相关性定义)来解决管网问题的算法,该方法特别适合求解边界条件由压力流量二次曲线定义的管网。Huang等^[21-22]开发了用于模拟和分析地热管网系统性能的计算机模型,该模型中使用网络节点和回路处的质量流量和压力平衡建立非线性方程组,具有较好收敛性。高鲁锋等^[23]研究了蒸汽管网的水力热力耦合计算方法,但未对用户流量分配的准确性做出验证。Karney等^[24]研究从能量守恒角度阐述管网瞬态行为,通过实际案例表明能量方程对某些部件设备水锤计算是有效的,使用能量方法是现有管网计算中一个有效补充。Wang等^[25]提出了一种环状网络的分析方法,可以处理环状蒸汽网络的非等温和可压缩流动特性等问题。

目前,多数对蒸汽管网的算法研究使用假设管网进行验证,本文结合热工流体网络理论,将蒸汽管网抽象为流体网络模型,与实际的管网运行参数进行对比。该模型的精度取决于模型的机理性、理论假设与特性参数的准确性,模型将管系内流体的交汇与分流问题简化为对节点压力和支路流量的瞬态求解问题,采用流体网络基本方程-质量守恒方程、动量守恒方程以及能量守恒方程,将压力与焓值相互耦合并进行非稳态求解,能够适应各种工况和参数。

1 数学模型

在这项研究中,输送管道内的供热蒸汽一般为过热蒸汽,可假设输送过程中没有相变,所以可以认为是单相可压缩流体。本研究中为构建模型所做的假设可以表述如下：

(1) 蒸汽管网流体网络内没有动力源。

(2) 节点内流体状态均匀(内部压力处处相等)。

(3) 流动阻力仅考虑局部节流阻力与管道摩擦沿程阻力,并设流动阻力系数为常数。

(4) 同一支路管道截面积不变,工质参数使用相连节点参数加权平均来表示。

构建的管网模型主要有以下两种组件：

(1) 节点,包括管网中管道的转折,网络中重要组件(厂家,用户等)。

(2) 分支,两个节点之间的联通组件。

特别的,管网中不同的对象在网络中其含义不同,如图1所示,节点可以分为网络流量入口的源节点、连接网络内部分支的中间节点和用户节点,用户节点一般为厂家。分支元素可用作模拟管道、弯头、阀门等组件。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 蒸汽供热管网的有向拓扑图

1.1 单相可压缩流体的网络模型

对稳态蒸汽管网,流动过程中的连续性方程(质量守恒)可以表示为

(1)$\begin{eqnarray} V_{i} \frac{{\rm d}\rho_{i} }{{\rm d}t}=\sum\limits_{j=1}^N {D_{ij} } G_{ij} \end{eqnarray}$

在蒸汽管网热量传输过程中,焓$h$的变化要比压力$p$的变化要缓慢,由

$\begin{eqnarray*} \frac{{\rm d}\rho }{{\rm d}t}=\frac{\partial \rho }{\partial p}\frac{{\rm d}p}{{\rm d}t}+\frac{\partial \rho }{\partial H}\frac{{\rm d}h}{{\rm d}t}\approx \frac{\partial \rho }{\partial p}\frac{{\rm d}p}{{\rm d}t} \end{eqnarray*}$

可得

(2)$\begin{eqnarray} C_{i} \frac{{\rm d}p_{i} }{{\rm d}t}=\sum\limits_{j=1}^N {D_{ij} G_{ij} } \end{eqnarray}$

式中,$C_{i}=V_{i}{\partial \rho_{i}}/({\partial p_{i}})$是节点$i$处工质的可压缩能力(kg/MPa);$p_i$是节点$i$处工质的压力;$\rho_i$是节点$i$处工质的密度;$t$是时间;$N$是节点总数;$G_{ij}$是节点$i$,$j$之间的质量流量;$V_{i}$是节点$i$的容积;$D_{ij}$是节点$i$,$j$之间的连接方式$(i=1,2,\cdots,N$; $j=1,2,\cdots,N)$,具体数值为

$\begin{eqnarray*} D_{ij}=\left\{ \begin{array}{ll} 1, & \mbox{节点$i$,$j$之间有连接,}\\&\mbox{流动方向由$j$指向$i$}\\ 0, & \mbox{节点$i$,$j$之间没有连接}\\ -1, & \mbox{节点$i$,$j$之间有连接,}\\&\mbox{流动方向由$i$指向$j$}\\ \end{array} \right. \end{eqnarray*}$

连续性方程表示了一个节点处的流量守恒的关系,该节点的流动状态受到和它相连的所有节点影响。图2显示了节点$i$与其相连的所有节点体积元素示意图,需要注意的是在逻辑上一个节点能与$N$个节点相连,但实际模型中一个节点至多与三个节点相连,所以在这个情况下该节点就是一个三通类型,其中$P$和$T$分别为对应节点处压力和温度。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 管道的第$i$个节点的拓扑结构示意图

流体模型中动量守恒方程可以写为

(3)$\begin{eqnarray} \rho_{ij} L_{ij} \frac{{\rm d}U_{ij} }{{\rm d}t}=D_{ij} \times \left( {P_{j} -P_{i} +D_{ij} \times H_{ij} } \right)-h_{\rm w} \end{eqnarray}$

式中,$L_{ij}$为节点$i,j$间管道的长度;$H_{ij}$是节点$i$,$j$之间宏观动能、势能及动力源产生的压力;$U_{ij}$是节点$i$,$j$之间的流体流速;$\rho_{ij}$是节点$i,j$之间流体的平均密度;$h_{\rm w}=\sum \left(0.5\lambda{L}/{d}+\xi \right)$是沿程阻力和局部阻力损失,$\lambda$是沿程阻力系数,$L$是管道长度,$d$是管道直径,$\xi$是管道阻力部件(例如弯头、三通等)的当量阻力系数。

根据管道惯性系数$I_{ij}={L_{ij}}/{A_{ij}}$,$A_{ij}$为节点$i,j$之间管道的截面积,管道的摩擦阻力系数$R_{ij}={h_{\rm w}}/\left(A_{ij}U_{ij}\rho_{ij}\right)^{2}$,且管道中没有动力源,将$H_{ij}=0$代入式(3)得

(4)$\begin{eqnarray} I_{ij} \times \frac{{\rm d}G_{ij} }{{\rm d}t}=D_{ij} \times \left( {P_{j}-P_{i} } \right)-R_{ij} \times G_{ij}^{2} \end{eqnarray}$

管网中的能量守恒方程可以写为

(5)$\begin{eqnarray} V_{i} \frac{{\rm d}\left( {\rho_{i} u_{i} } \right)}{{\rm d}t}=\sum\limits_{j=1}^N{D_{ij} } G_{ij} h_{j} +Q_{i} \end{eqnarray}$

式中, $V_{i}$是节点$i$的容积;$u_{i}$是节点$i$的内能;$h_{j}$是节点$j$的焓;$Q_{i}$是节点$i$的热量。

由于$\rho u=\rho \left( h-pv \right)=\rho h-p$,可得

$\begin{eqnarray*} v\frac{{\rm d}\left( \rho u \right)}{{\rm d}t}=vh\frac{{\rm d}\rho }{{\rm d}t}+v\rho \frac{{\rm d}h}{{\rm d}t}-v\frac{{\rm d}p}{{\rm d}t} \end{eqnarray*}$

结合式(1)并代入式(5),可以得到

(6)$\begin{eqnarray} M_{i} \times \frac{{\rm d}h_{i} }{{\rm d}t}=\sum\limits_{j=1}^N {D_{ij} } \times G_{ij}\times (h_{j} -h_{i} )+ Q_{i} +V_{i} \frac{{\rm d}p_{i} }{{\rm d}t} \end{eqnarray}$

式中,$M_{i}=V_i\rho_i$,是节点$i$内流体质量;$h_i$是节点$i$的焓;$Q_i=\gamma \big[T_{\rm env}$ $-$ $0.5\left( T_{\rm in}+T_{\rm out} \right)\big]$是换热量,$T_{\rm env}$是环境温度,$T_{\rm in}$和$T_{\rm out}$分别是流进和流出的气体温度,$\gamma$是管段上的散热系数;$V_{i}{{\rm d}p_{i}}/{{\rm d}t}$是推进功对流体温度的影响,通常比传热的影响要小,所以可以忽略此项作用,改为

(7)$\begin{eqnarray} M_{i} \times \frac{{\rm d}h_{i} }{{\rm d}t}=\sum\limits_{j=1}^N {D_{ij} } \times G_{ij} \times (h_{j} -h_{i} )+Q_{i} \end{eqnarray}$

内部节点与环境(定义为第$N$节点)之间的物质交换可以表示为

(8)$\begin{eqnarray} G_{i,N} =\frac{C_{i} \left( {p_{i} -p_{\rm a} } \right)}{T_{i}^{\rm c} } \end{eqnarray}$

式中,$p_{\rm a}$是环境大气的压力(MPa);$T_{i}^{\rm c}$是孤立节点$i$泄露到环境大气的时间常数(s)。

1.2 方程组的进一步简化

方程(2),(4),(6)是非线性微分、代数等式。对于动态仿真,重要的要求是要保证实时性,并且要求计算流程的鲁棒性高。

式(2)表示节点$i$压力与流量关系,流量常有迟滞。因此结合式(2)和式(7)可以写作

(9)$\begin{eqnarray} C_{i} \frac{{\rm d}p_{i} }{{\rm d}t}=\sum\limits_{j=1}^N {D_{ij} } \sqrt {\frac{D_{ij}\left( {p_{j} -p_{i} } \right)}{R_{ij} }} +\frac{C_{i} \left( {p_{i} -p_{\rm a} } \right)}{T_{i}^{\rm c} } \end{eqnarray}$

为保证动态仿真算法的实时性和稳定性,采用稳定的隐式欧拉积分算法,由式(7)和式(9)可得

(10)$\begin{eqnarray} M_{i}^{r} \times \frac{h_{i}^{r+1} -h_{i}^{r} }{\Delta t}=\sum\limits_{j=1}^N {D_{ij}^{r} } \times G_{ij}^{r} \times (h_{j}^{r+1} -h_{i}^{r+1} )+V_{ij} \left[ {\frac{1}{2}\left( {T_{i}^{r+1} +T_{j}^{r+1} } \right)-T_{\rm a} } \right]\\ \end{eqnarray}$

(11)$\begin{eqnarray} C_{i}^{r+1} \frac{p_{i}^{r+1} -p_{i}^{r} }{\Delta t}=\sum\limits_{j=1}^N {D_{ij}^{r} } \sqrt {\frac{D_{ij}^{r} \left( {p_{j}^{r+1} -p_{i}^{r+1} } \right)}{R_{ij} }} +\frac{C_{i}^{r+1} \left( {p_{i}^{r+1} -p_{\rm a} } \right)}{T_{i}^{\rm c} } \end{eqnarray}$

式中,$r$是离散时间的变量,时间$t=t_{0}+r\Delta t$,$r=0,1,2,\cdots$。

式(10)和式(11)是完全解耦的,在动态仿真过程中,先求解式(11)组成的$N$阶非线性代数方程组,可以得到各节点压力,根据这个压力可以求出各管道的流量,最后代入式(10)构成的非线性代数方程组,就可以得到各节点温度。小扰动条件下,$C_{i}^{t+1}$,$T_{i}^{t+1}$,$M_{i}^{t+1}$可以分别用$C_{i}^{t}$,$T_{i}^{t}$,$M_{i}^{t}$替代,对精度影响较小,用以减少运算量。

1.3 线性方程的迭代解法

在1.2节,我们已经得到了可以用于计算的方程,综合考虑水力工况和热力工况的相互影响,将三大守恒方程联立,在一个时间步长内同时求解各节点的压力和焓值。耦合之后得到的是各节点的焓值和压力关于时间的一阶微分方程组,可采用经典四阶龙格库塔法求解该方程组,实现蒸汽管网动态仿真。不考虑支路惯性,模型中的非线性项主要为流体流动损失$R_{ij}^{r}\left(G_{ij}^{r} \right)^{2}$,可以使用$G_{ij}^{r} G_{ij}^{r+1}$近似代替,得到

(12)$\begin{eqnarray} G_{ij}^{r+1} =\frac{D_{ij} \left( {p_{j}^{r+1} -p_{i}^{r+1} }\right)}{R_{ij}^{r} G_{ij}^{r} } \end{eqnarray}$

代入式(11)节点的质量守恒方程,得到

(13)$\begin{eqnarray} C_{i}^{r+1} \frac{p_{i}^{r+1} -p_{i}^{r} }{\Delta t}=\sum\limits_{j=1}^N {\frac{p_{j}^{r+1} -p_{i}^{r+1} }{R_{ij}^{r} \times G_{ij}^{r+1} }} +C_{i}^{r+1} \frac{p_{i}^{r+1} -p_{\rm a} }{T_{i}^{\rm c} } \end{eqnarray}$

整理为矩阵形式

(14)$\begin{eqnarray} \mathbf A^{r+1}\mathbf P^{r+1}=\mathbf B^{r+1} \end{eqnarray}$

其中

$\begin{eqnarray*} &&\mathbf P^{r+1}=\left[ p_{1}^{r+1}\, \, \, p_{2}^{r+1}\, \cdots \, p_{N}^{r+1} \right]\\ &&\mathbf A^{r+1}=\left[ a_{ij}^{r+1} \right], \ \ \mathbf B^{r+1}=\left[ b_{1}^{r+1}\, \, \, b_{2}^{r+1}\, \, \cdots \, b_{N}^{r+1}\right]\\ &&a_{ii}^{r} =\sum\limits_{j=1}^N {\frac{1}{R_{ij}^{r} G_{ij}^{r} }}+\frac{C_{i}^{r} }{\Delta t}+\frac{C_{i}^{r} }{T_{i}^{\rm c} }, \quad i=1,2,\cdots, N\\ &&a_{ij}^{r} =-\frac{D_{ij}^{2}}{R_{ij}^{r} G_{ij}^{r} }, \quad i\ne j\\ &&b_{i} =\sum\limits_{j=1}^N {\frac{p_{j}^{r-1} }{R_{ij}^{r} G_{ij}^{r} }}+\sum\limits_{j=1}^N {\frac{D_{ij} H_{ij}^{r} }{R_{ij}^{r} \cdot G_{ij}^{r-1} }} +\\&&\qquad \frac{C_{i}^{r} p_{\rm a} }{T_{\rm C} }+\frac{C_{i}^{r} \cdot p_{i}^{r-1} }{\Delta t} \end{eqnarray*}$

可得到压力矩阵,首先求解压力矩阵,得到压力,再根据压力计算出流量,然后将流量代入节点能量方程,即可解出节点的焓值。

同样由式(10)得到节点的能量守恒方程

(15)$\begin{eqnarray} M_{i}^{r} \times \frac{h_{i}^{r+1} -h_{i}^{r} }{\Delta t}=\sum\limits_{j=1}^N {D_{ij}^{r} } \times G_{ij}^{r} \times h_{ij}^{r} +Q_{i}^{r} \end{eqnarray}$

整理为矩阵形式

(16)$\begin{eqnarray} \mathbf E^{r-1}\mathbf H^{r}=\mathbf F^{r-1} \end{eqnarray}$

其中

$\begin{eqnarray*} &&\mathbf H^{r}=\left[ h_{1}^{r}\, \, \, h_{2}^{r}\, \cdots \, h_{N}^{r} \right], \ \ \mathbf E^{r-1}=\left[ e_{ij}^{r-1} \right] \\ &&\mathbf F^{r-1} =\left[ f_{1}^{r-1}\, \, \, f_{2}^{r-1}\, \, \cdots \, f_{N}^{r-1}\right]\\ &&e_{ii}^{r} =\frac{M_{i}^{r} }{\Delta t},\ \ e_{ij}^{r} =-D_{ij}^{r} G_{ij}^{r},\ \ f_{i}^{r} =Q_{i}^{r} +\frac{M_{i}^{r} }{\Delta t}h_{i}^{r} \end{eqnarray*}$

上文的公式是计算中的具体矩阵函数,作为联立方程的基础,对每个节点建立的方程有两个,将密度表示为压力和焓值的函数$\rho =\rho(P,h)$,对时间求导后联立的质量方程和能量方程为

(17)$\begin{eqnarray} \left.\begin{array}{l} {\dfrac{{\rm d}P_{i} }{{\rm d}t}=f_{i1} \left( {P_{1},P_{2},\cdots,P_{N} ;h_{1},h_{2},\cdots,h_{N} } \right)}\\[3mm] {\dfrac{{\rm d}h_{i} }{{\rm d}t}=f_{i2} \left( {P_{1},P_{2},\cdots,P_{N} ;h_{1},h_{2},\cdots,h_{N} } \right)}\\ \end{array} \right\} \end{eqnarray}$

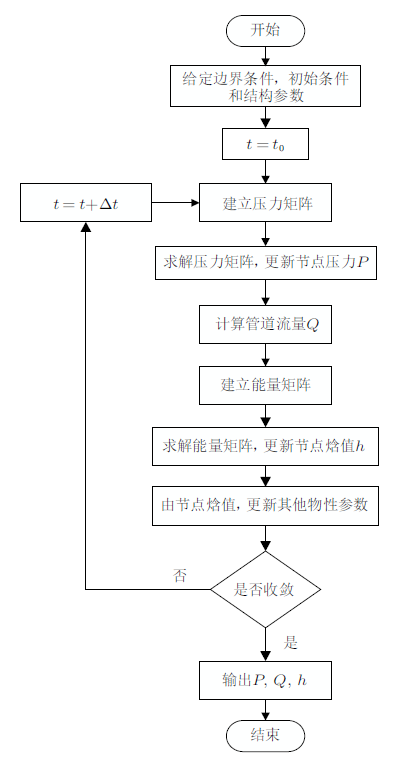
对$N$个节点,能得到一个具有2$N$个方程的一阶微分方程组,共有2$N$个待求变量,因此,方程组是封闭的,其计算流程如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 动态仿真算法流程示意图

2 算例验证

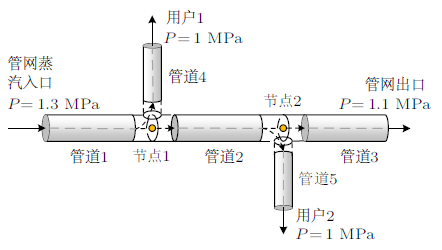
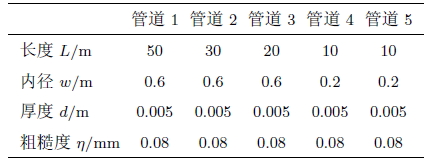
为说明耦合解法的功能,我们设计了一个假设的管网模型,其中蒸汽从蒸汽入口通入,作为管网的入口,沿途经过两条用户支路,最后流向管网出口,如图4所示,该管网系统总共有5条管道,这些管道的几何参数如表1所示。在定义边界条件的过程中,可以给定压力或流量,我们采用给定压力边界的方式,压力大的一端即为入口。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 示例仿真管网示意图

表1 仿真测试结构参数表

新窗口打开| 下载CSV

在图4所示的管网中,计算从管网入口开始,从给定的管网入口压力计算出管道1的出口,即节点1的压力。对于管道2,其入口压力指定为管道1的出口压力,管道3的入口压力指定为管道2的出口压力,对其他管道的操作是同样的。在压力迭代完成后,依次对流量和焓值进行迭代计算,重复该程序直到管网中各状态参数稳定。

采用Fluent计算实验仿真平台验证我们的计算结果,Fluent计算实验仿真平台通过对给定的流体模型进行流域建立、网格划分及求解计算,得出流体模型内的流场特征及流场分布,其求解结果比较精确,可以作为实验对照组。由于管道较短,温度降低不是很显著,所以采用绝热模型。

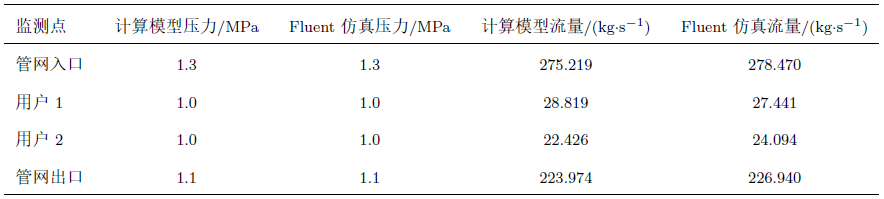
表2给出了两种方式的模拟结果,在1.3 MPa的入口压力下,我们的管网计算模型与计算机实验仿真结果流量十分接近,从结果分析,管道4相比于管道5更接近入口,在同样的结构条件下,分配的流量更多,在两种计算结果中显示了这一点。管道4和管道5的流量在Fluent中的流量相差较小,而计算模型的流量相差较大,这是由于在Fluent中流体流动更接近于实际状态,在管道三通处会存在压力分布不均、壁面处会产生边界层分离等问题,这会导致流阻比我们的计算模型更大,所以管道4流量比计算模型低。而对于管道5的流量,计算模型的流量低于Fluent仿真,这是由于计算模型采取压力边界条件,在同样的供汽压力下,程序中的流量为275.2 kg/s,低于Fluent的流量278.5 kg/s,且在管道4处分流较多,导致管道5的流量偏低。

表2 Fluent计算机实验仿真和计算模型的结果对比

新窗口打开| 下载CSV

结果表明,计算模型所得出的结果与计算机实验仿真结果接近,存在的误差主要由于管网结构在微观细节上的不同,这一点在计算方法中需要加入局部阻力部件的管损模型,就可以使得我们构建的管网模型更精确。因此,在这个实例中,验证了我们所构建的蒸汽管网动态仿真算法的有效性。

3 结果和讨论

为了测试和验证耦合算法程序在实际运行规则下的计算结果,在模拟计算中使用了中国临港某热电厂蒸汽管网数据,管网现场部分情况如图5所示,管道布局长度在3 km左右,有13个用户。在一系列模拟计算中,对比了程序的运行和实际参数的结果。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 临港蒸汽管网现场图

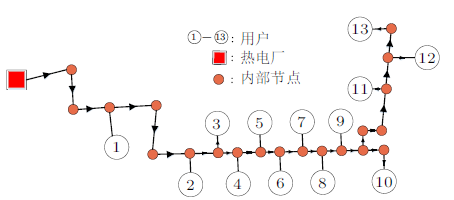
结合网络元与网络拓扑理论,对现场蒸汽管网结构进行重构,可以得到如图6所示蒸汽管网概念模型,其中包含一个热电厂,十三家用户,用户编号是1到13。每条管道的预期流向都被标注,网络没有回路,本文的耦合算法可以应用在这样的管网结构上。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 临港热电厂蒸汽管网结构图

取一组临港某热电厂用户开阀较多的某工作日时刻蒸汽管网运行状态作为参照,热电厂蒸汽入网压力为1.36 MPa,温度为243${^\circ}$C,流量为53.239 kg/s,在程序中建立管网模型,供汽入口处的参数取管网入口实际参数,进行动态仿真计算,结果如表3所示。

表3 动态仿真结果与运行数据对比

新窗口打开| 下载CSV

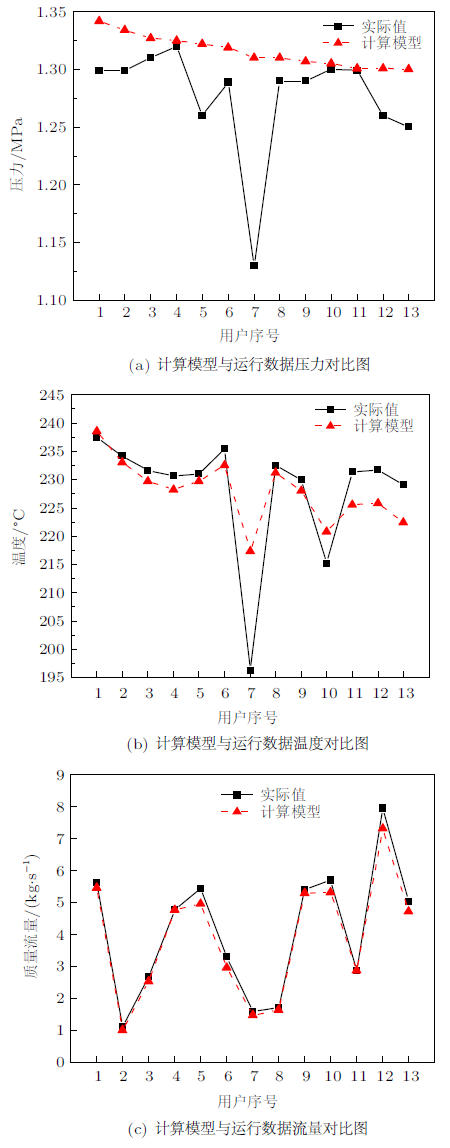
计算模型与现场运行数据对比见图7。从表3与图7可以进行分析,由于动态仿真计算考虑了蒸汽流动过程中的状态变化,将压力、焓值在迭代过程中不断更新与反馈,温度与流量的计算结果与实际运行数据吻合度较好,温度误差多在5%以内,小流量的情况下流量的波动使得误差结果多在10%以下。值得关注的是压力的对比情况,可以发现计算模型的压力由于沿途的管损不断降低,而现场压力计所采得的压力曲线波动较大,主路管线的压力并没有呈现出合理的压降关系。某些用户不仅在压力,且在温度上明显与周围厂家差异较大,这可能是由现场压力计的读数波动或者数据读取延时所造成的,我们有理由认为这部分压力或温度可能不准确。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 计算模型与现场运行数据对比图

结果表明,用户在各工况下的流量仿真结果均贴近实际测量数据,但计算过程中仍存在一定的偏差,这是由于构建的管网结构较为简单,现场管网存在多弯管、多阀门,管网结构老化、凝结水等一系列问题,针对这种问题,需要对现场实际情况进行调查,在管网模型中添加流阻变量,并不断调整相关参数,使得管网结构更趋向于实际结构,仿真结果更准确。

4 结论

本文提出了一种新的蒸汽供热网络动态仿真方法,它利用了内部流体参数的守恒关系,用于模拟流体管路的温度、压力、流量的非稳态特性,具有计算迅速、参数可控等特点,可解决目前热电联产过程中蒸汽管网的供汽计算忽略热力损失对管网压力影响所导致计算结果误差偏大的问题。在计算过程中,由于局部散热,压力突变等问题,蒸汽输送过程中的热力参数比较多变,因此水蒸气的热力性质比单纯的供水管网更为复杂,须采用实际气体状态方程求解蒸汽流动过程中的状态参数,本文采用IAPWS-IF97工业标准中过热蒸汽区参数状态方程,用于求解蒸汽流动过程中密度、压缩因子等参数。

与实际蒸汽管网运行数据作对比,结果较为吻合。示例验证表明,管网的动态仿真计算中压力、温度与流量相对误差在10%以下,计算结果精度较高,可以应用于管网状态监测、运行故障诊断、管网优化设计等方面。进一步的工作在于管网实际结构的精确化建模,包括阻力部件、三维空间上管线布局带来的损失等,从而可以使得结果更具参考价值。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Pen

, Shen

Study on near distributed dynamic model of a multifountain-and-multiconfluent network system of steam main-pipeline and parallel coursing units

Multiphase Flow, Macau, China, 2006