梁柱结构不仅是建筑工程和桥梁工程的主要结构形式,也是轮船、飞机机翼和起重机等机械结构中的重要承力构件。鉴于梁弯曲变形是杆件结构基本变形中最为复杂的变形形式,对梁弯曲变形的研究历史也最为曲折,对其中最为关键的中性轴位置的确定也经历了诸多学者的努力和不断探索。
梁的中性层是指弯曲变形时梁内纵向长度不变的一层,或者说弯曲变形时梁内既不伸长也不缩短的一层,而梁的中性轴指梁中性层与其横截面的交线。由单一机械载荷作用下梁的纯弯曲试验可知,弯曲后梁的纵线由直线变为弧线,靠近梁顶面或梁底面一侧的纵线伸长,而另一侧的纵线缩短,因此弯曲变形时梁内总有一层既不伸长也不缩短,即梁中性轴总是存在的[1-2];在梁中性轴位置即坐标轴确定之后,便可由经典的单变量方法描述梁的弯曲正应变,即$\varepsilon=y/\rho$,其中$y$为考察点距离中性轴的坐标,$\rho$为中性轴处的曲率半径;而后便可进一步确定梁的弯曲正应力分布,即在梁的中性轴处弯曲正应力为零,在中性轴两侧,一侧正应力为正,而另一侧正应力为负,且正应力的大小与到中性轴的距离成正比。
1 梁中性轴的早期认识
对中性轴位置的正确回答要归功于胡克对梁中正应力分布的正确认识,1678年胡克在《论弹簧》一书中指出梁中正应力是以中性轴处为零的线性分布,一侧受拉,而另一侧受压。然而,很难知道哪一层的正应力为零,那么只好借助梁截面轴向力平衡条件,即梁上弯曲轴力或净纵向力为零,或者说整个梁横截面上的正应力合力为零的条件,来确定中性轴位置。当材料服从胡克定律时,根据梁中正应力关于中性轴的分布方式可知,梁的中性轴必然通过截面形心。既然中性轴通过截面形心,当材料服从胡克定律时确定中性轴位置就比较容易了。对于具有对称结构的梁而言,对称轴就是中性轴;但对于具有非对称结构的梁,中性轴的确定需要计算组合截面的形心位置。
2 梁中性轴的当代进展
面对工程中新材料和新结构形式的大量使用,梁中性轴位置的确立又日益变得重要。当梁结构材料不服从单一的经典胡克定律时,梁中正应力关于中性轴的分布方式必然发生变化,导致梁的中性轴不再通过截面形心,中性轴位置一般仍然需由隔离体的轴向力平衡条件直接确定。而材料不服从单一胡克定律的情况也有诸多情形,有的是因为材料的非线性性质引起,如双模量梁、含损伤梁、弹塑性梁、功能梯度形状记忆合金梁等;有的是因为复杂加载条件或多物理场(热机耦合、热电耦合、磁电)因素引起,如考虑热扩散影响的梁、考虑压电影响的梁等;有的是因为结构因素引起,如叠合梁和层合梁等。
图1
图2
图3
图4
图5
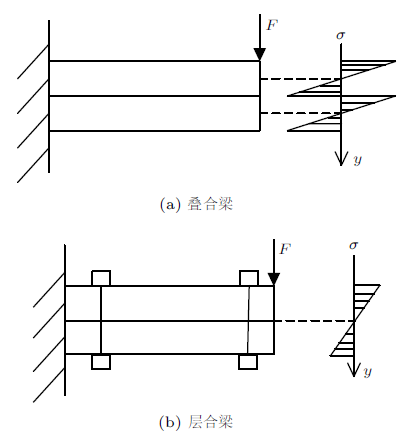
土木工程中通常采用叠合、焊接和粘接等加固法形成叠合梁和层合梁对原有结构进行加固处理,若两梁接触面光滑则称为叠合梁,若两梁加固成整体且无相对滑动则称为层合梁。如图6所示,对于叠合梁而言,每根小梁有各自的中性轴,均通过各自的形心,且正应力按各自的中性轴正比分布[14];当叠合梁中两梁接触面有摩擦时,上下梁的中性轴都由相应的形心向接触面偏移,即上梁中性轴位于其形心下方,下梁中性轴位于其形心上方[15]。对层合梁可由直接分析法,根据脱离体轴向力平衡条件或等效截面法(相当截面法)求得中性轴位置,其位置一般与各层面积和材料弹性模量有关。对两类不同材料层合梁而言,中性轴会偏离几何中心而向高弹性模量区移动[16-17]。
图6
值得一提的是,在解决多物理场作用下新材料、新结构的力学问题时,大多数研究采用单变量方法描述结构的应变场,但单变量方法限制坐标系建立在中性轴上,所以中性轴的确定成为问题的关键,或者说,中性轴的位置成为力学模型中一个隐含的变量,可见需要发展更为简洁的描述方法。
3 微纳层合梁的中性轴问题
近年来,利用微纳制造技术和现代传感技术等制备的微梁层合结构,因其具有无需标记、快速、实时、高灵敏度和方便携带等优点,在医学检测、环境监测、医药开发和军事安全等领域有广泛的应用,吸引了众多学者的关注。正如前面所述,对于梁理论而言,如何描述梁的应变场是关键所在。在经典宏观梁的单变量理论中,应变场的度量或其坐标系的基准是中性轴,所以利用经典方法时必须先确立梁中性轴的位置。但对于微纳梁而言,由于具有较大的表体比,需要计入通常简化为切向作用的表面应力效应,或需要引入表征非局部效应的非经典连续介质本构关系[18-19],加之需要考虑器件服役时多物理场的耦合作用,这些新的效应给微纳梁结构中性轴的定位问题带来了挑战。
关于层合梁问题,针对热适配问题,早在1925年,Timoshenko[20]提出了先在各层寻找中性轴再利用层间连续条件的叠加法,但当结构层数过多时,方程求解变得较为繁琐;针对压电层合结构问题,Weinberg[21]放弃了将坐标系建立在中性轴上的经典思维范式,提出了以中性轴位置作为新变量显示化在应变场描述中的两变量方法;Hsueh[22]将原来一个轴向力为零的平衡方程拆解为均匀应变和弯曲应变引起的轴力分别为零的两个方程,提出了寻找弯曲轴的Hsueh三变量法;针对功能梯度材料梁问题,Zhang等[23]提出了与寻找弯曲轴方法类似的物理中面法;Zhang等[24-25]基于两个参考面提出了更为简洁的张氏两变量法,即$\varepsilon =\varepsilon_{0}-y/\rho$,其中$\varepsilon_{0}$为坐标轴处的正应变,$\rho$仍为中性轴处的曲率半径;该方法既不同于将坐标系建在中性轴上的经典单变量方法[1-2],也不同于Freund提出的基于一个参考面描述应变场的两变量假设法[26]。目前张氏两变量新方法已广泛用于核冷却系统、光伏电池、钻井套管、电阻式存贮器、铺设路面和热障涂层等设计研究中[27-32]。
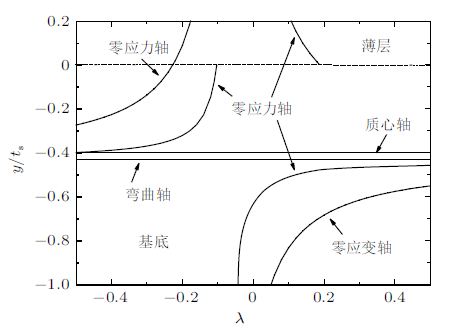
值得注意的是,当分子或原子吸附在微梁的上下表面会形成表面应力差,这个吸附表面应力会引起微梁的弯拉或弯压组合变形,变形后微梁的中性轴位置会发生变化,如图7所示,在微梁上表面受拉吸附应力作用下,吸附稳定后微梁的中性轴位置将下移,下移量取决于微梁功能层和基底层的厚度和弹性模量[33]。对于均匀温度场和机械载荷作用下的层合微梁,如图8所示,随着加载参数比$\lambda$的变化,零应变轴是唯一的,但零应力轴可能不唯一,换句话,零应力轴的个数和位置取决于弹性模量、基底和膜的厚度比、力学和温度加载条件[34-35],这势必给基于零应力确立中性轴 (即零应变轴)位置的传统单变量方法带来挑战,而借助上述Hsueh三变量法[22]和张氏两变量法[24-25]等可巧妙地规避这一难题。
图7
图8
4 结语
梁中性轴位置的确定是预测梁结构变形和应力分布的基础,也是进而解决梁强度、刚度、稳定性问题的关键。首先,诸多前辈基于中性轴概念,历经一百多年的探索,给出了描述应变场的单变量方法,获得了纯弯曲均质梁中性轴必然通过其截面形心的基本结论。后来随着新材料和新结构的不断涌现,如双模量梁、含损伤梁、弹塑性梁、层合梁、组合梁、考虑热效应的梁、压电梁、功能梯度梁和形状记忆合金梁等,使得中心轴的漂移成为必须解决的棘手问题。而近二十年微纳梁结构中的表界面效应、非局部效应和多物理场耦合效应进一步推动发展了更为精确和简便的Hsueh三变量方法、物理中面法、张氏两变量方法等。对于梁中性轴问题的历史回顾和正确认识对于合理有效地解决建筑、桥梁、机械结构、微电子器件等相关问题有重要的现实意义。
参考文献
梁中性轴简史试编
The history on neutral axle of beam
说梁——力学史札记之十九
A brief talk about the development of the theory of elastic beam
不同模量理论弹性支承连续梁及框架
The elastic supported continuous beam and frame of different modulus
圆钢管混凝土受弯构件中性层偏移规律及承载力研究
Study on neutral layer migration law and flexural capacity about the concrete flied circular steel tubular flexural members
功能梯度梁纯弯曲特性研究
Analysis of functional gradient material beam subjected to pure bending
关于轴向力作用下梁弯曲时中性轴位置的讨论
Discussion of neutral axis position of beam bending under the action of axial force
形状记忆合金梁纯弯曲的理论分析
Theoretical analysis of shape memory alloy beam subjected to pure bending
叠梁的应力分析与实验
Experiment and analysis on normal stress in superposed beam
叠梁的分析与实验
Analysis and experiment of folding girder
双材料层合梁的弯曲切应力分析
Analysis of shearing stress in bending of bi-material laminated beam
层合梁弯曲正应力的测试与计算
Test and computation of normal bending stresses in laminated beams
Analysis of bi-metal thermostats
Working equations for piezoelectric actuators and sensors
Thermal stresses in elastic multilayer systems
A theoretical analysis of FGM thin plates based on physical neutral surface
An alternative model for elastic bending deformation of multilayered beams
Thermoelastic stresses in multilayered beams
Some elementary connections between curvature and mismatch strain in compositionally graded thin films
Shakedown analysis of multilayered beams coupled with ductile damage
Multi-inch single-crystalline perovskite membrane for high-detectivity flexible photosensors
Mechanism of collapse failure and analysis of yield collapse resistance of casing under combined load
Temperature-dependent fatigue failure of flexible poly(9,9-dioctylfluorene-alt-benzothiadiazole) (PFBT)$-$ZnO nanoparticle hybrid resistive switching memory devices
热应力作用下层合路面结构层间剥离内力分析
Interlayer peeling internal forces of laminated pavement structures subjected to thermal stresses
Size-dependent electro-thermo-mechanical analysis of multilayer cantilever microactuators by Joule heating using the modified couple stress theory
压电微悬臂梁气体传感器静态弯曲模型的研究
Research on static bending model of piezoelectric microcantilever gas sensors
An alternative two-variable model for bending problems of multilayered beams
An alternative model for elastic thermal stresses in two materials joined by a graded layer