自2008年北京奥运会上自平衡的赛格威车首次亮相以来[1 ] ,2015年出现了赛格威车缩小版的自平衡双轮滑板车[2 ] 。与此同时,又有构造更简单的称为"Onewheel"的自平衡独轮滑板车问世 (图1 )[3 ] 。这种新型的代步工具只有一个轮子,仅依靠驾车人的身体动作就能实现加速、减速和转弯等各种功能。虽然操纵难度比双轮滑板车更大,需要掌握更多技巧才能熟练驾驶,但骑手能感受到自由飞翔般地飘浮感觉,因而备受年轻人的青睐。各种新设计和产品不断涌现,促使自平衡滑板车的技术和产业在国内快速发展。
图1
自平衡滑板车的出现为力学科普提供了一个有趣的课题。重心高高在上的骑手如同一只倒置的复摆,稳定的自平衡是如何实现的?根据经典力学的基本原理,任何系统的运动状态只能依靠外力的作用改变。自平衡滑板车仅靠驾车人扭动身体就能改变运动状态应如何解释?独轮车与地面只有一个点接触,约束力不能形成绕垂直轴的力矩,转弯的动力从何而来?就上述问题本文讨论自平衡独轮滑板车的动力学原理。忽略骑手肢体动作引起的质量变化,将车架加骑手视为刚体,与车轮组成双刚体系统。设车轮相对地面做纯滚动,滑板车的运动被归结为非完整约束条件下双刚体系统的动力学问题。
自平衡独轮滑板车的构造十分简单。在钢制框架的中心用轴承安装一只粗壮的橡胶轮,前后各装有一片木踏板 (图2 )。骑手跨立在车轮前后两侧,通过重心移动改变足底对前板或后板的压力。板内安装的加速度计将测出的信息通过控制系统传输至驱动电机,以控制车轮的加速或减速。
图2
需要转弯时,与驾驭滑雪板或冲浪板的方法类似,驾车人带动车体向要转弯的一侧倾斜。利用与自行车类似的"离心力效应" 和"陀螺效应",倾斜车体的重力与支承力构成力偶,使旋转中的车轮进动,出现绕垂直轴的转动。由此产生的陀螺力矩与重力矩平衡[4 ] 。车体绕垂直轴的转动使直线轨道发生偏转,从而实现转弯动作。沿曲线轨道行进的车体和人体产生离心惯性力,使驾车人恢复直立姿态避免摔倒。独轮滑板车厚重车轮的动量矩明显大于自行车的前轮,陀螺效应也更为明显。
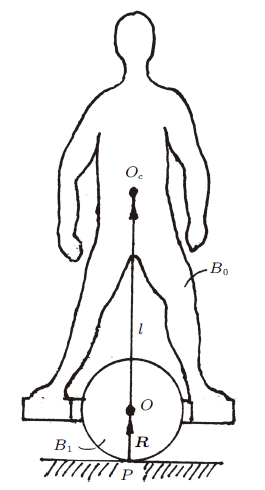
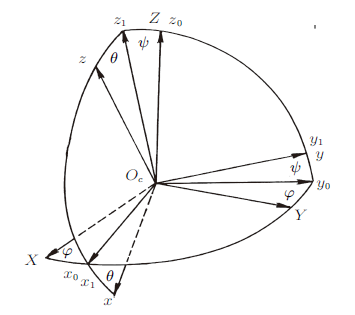
将车架和固定在车架上的骑手作为刚体$B_{0}$,车轮作为刚体$B_{1} $。独轮滑板车是由$B_{0}$和$B_{1} $以圆柱铰连接组成的双刚体系统$\left\{ B\right\}$ (图3 ),其中,$R$为车轮半径,$B_1$与地面的接触点记为$P$。将车轮不转时$\left\{ B\right\}$固结成的刚体记作$B_{{\ast}} $。以$B_{{\ast}} $的质心$O_{c} $为原点,建立平动参考坐标系$\left( {O_{c} -XYZ}\right)$,$X$和$Y$轴与地面平行,$Z$轴为垂直轴。设$\left( {O_{c} -XYZ}\right)$绕垂直轴转过$\varphi $角的位置为$\left( {O_{c} -x_{0} y_{0} z_{0} }\right)$,$x_{0} $轴为车轮的前进方向。继续绕$x_{0} $轴转过$\psi $角为$\left({O_{c} -x_{1} y_{1} z_{1} } \right)$,$y_{1}$轴为车轮的旋转轴。最终$\left( {O_{c} -x_1y_1z_1}\right)$绕$y_{1} $轴转过$\theta$角为刚体$B_{{\ast}} $的主轴坐标系$\left( {O_{c} -xyz}\right)$,$z$轴沿骑手身体的纵轴(图4 )。
图3
图4
以骑手在车板上直立,滑板车匀速直线前行作为稳态运动。即$\varphi =\theta =\psi=0$,$\varOmega =\varOmega_{0} $,质心速度$v_{cx} =R\varOmega_{0} $,$v_{cy}=0$。其中$\varOmega$为转速,$\varOmega_{0}$为稳态转速。骑手利用身体向前或向后的倾斜动作控制车速。当骑手向前倾斜时,因重力对前板的压力大于后板,使车板产生角加速度$\ddot{{\theta}}$。安装在车板内的加速度计将测出的$\ddot{{\theta}}$信息输入控制系统,积分后转换为转角$\theta $和角速度$\dot{{\theta}}$信息,控制驱动力矩使车轮加速。如向后倾斜则控制力矩方向相反,车轮减速。即使在稳态行进过程中,若骑手因扰动向前倾斜,车体会自动加速,产生向后的惯性力使骑手恢复原位。向后倾斜则减速产生向前的惯性力。因此这种速度控制系统也是骑手站立稳定性的根本保证。
仅保留小量$\varphi $, $\theta $, $\psi$及其导数的一次项,设$\mathbf i$, $\mathbf j$, $\mathbf k$为$x$, $y$, $z$各轴的基矢量,$B_{{\ast}} $的角速度为$\mathbf \omega=\dot{{\psi }}\mathbf i+\dot{{\theta}}\mathbf j+\dot{{\varphi }}\mathbf k$。设$B_{1}$相对$B_{{\ast}} $的旋转速度为$\mathbf \varOmega=\varOmega\mathbf j$,从$B_{1} $的质心即轮心$O$至$B_{{\ast}} $的质心$O_{c} $引矢径$\mathbf l=l\mathbf k$,从$B_{1}$与地面的接触点$P$至轮心$O$引矢径$\mathbf R=R\mathbf k$ (图3 )。设$O_{c}$的速度为$\mathbf v_{c} =v_{cx} \mathbf i+v_{cy} \mathbf j+v_{cz}\mathbf k$,则$P$点的速度为$\mathbf v_{P} =\mathbf v_{c} +\left({\mathbf R+\mathbf{l}} \right)\times \mathbf \omega+\mathbf R\times\mathbf \varOmega$,导出
(1) $\begin{eqnarray} &&\mathbf v_{P} =\left[ {v_{cx} -R\varOmega -\left( {R+l} \right)\dot{{\theta }}} \right]\mathbf i+\\&&\qquad\left[ {v_{cy} +\left( {R+l} \right)\dot{{\psi }}} \right]\mathbf j+v_{cz} \mathbf k \end{eqnarray}$
设车轮$B_{1} $在地面上作无滑动的纯滚动,令$\mathbf v_{P}
(2) $\begin{eqnarray} \left.\begin{array}{l} v_{cx} -R\varOmega -\left( {R+l} \right)\dot{{\theta }}=0\\ v_{cy} +\left( {R+l} \right)\dot{{\psi }}=0\\ v_{cz} =0 \end{array}\right\} \end{eqnarray}$
利用此约束条件确定质心速度$\mathbf v_{c} $,即
(3) $\begin{eqnarray} \mathbf v_{c} \mathbf{=}\left[ {R\varOmega +\left( {R+l} \right)\dot{{\theta }}} \right]\mathbf i-\left( {R+l} \right)\dot{{\psi }}\mathbf j \end{eqnarray}$
将参考坐标系的原点$O_{c} $移至轮心$O$,设$\left\{ B\right\}$的质量为$m$,以$\left( {O-xyz} \right)$为参考坐标系,列写$\left\{ B\right\}$在重力$m\mathbf{g}$和约束力$\mathbf{F}$作用下的质心运动方程
(4) $\begin{eqnarray} \frac{{\tilde{{\rm d}}}\mathbf v_{c} }{{\rm d}t}+\mathbf \omega\times \mathbf v_{c} ={m\mathbf g}+\mathbf{F} \end{eqnarray}$
其中波浪号表示动坐标系$\left( {O-xyz}\right)$中的局部导数。将式(3)代入,解出约束力$\mathbf{F}$,即
(5) $\begin{eqnarray} \left.\begin{array}{l} F_{x} =m\left[ {R\dot{{\varOmega }}+\left( {R+l} \right)\ddot{{\theta }}-g\theta } \right] \\ F_{y} =m\left[ {R\varOmega \dot{{\varphi }}-\left( {R+l} \right)\ddot{{\psi }}+g\psi } \right] \\ F_{z} =m\left( {g-R\varOmega \dot{{\theta }}} \right) \\ \end{array}\right\} \end{eqnarray}$
设车轮$B_{1} $的质量为$m_{1}$,对$O$点的极惯量矩为$J_{0} $,动量矩为$\mathbf{L}_{1} =J_{0}\left( {\varOmega +\dot{{\theta }}} \right)\mathbf j+\cdots$,省略号为含$\dot{{\psi }},\dot{{\varphi}}$的小量。外力矩为电机驱动力矩$\mathbf{M}_{c} =M_{c}\mathbf j$和约束力$\mathbf{F}$对$O$点的主矩$\mathbf{F}\times\mathbf R$。以$\left( {O-xyz}\right)$为参考坐标系,列写$B_{1} $对质心$O$的动量矩定理
(6) $\begin{eqnarray} \frac{\tilde{\rm d}\mathbf{L}_{1} }{{\rm d}t}+\mathbf \omega\times \mathbf{L}_{1} =\mathbf{M}_{c} +\mathbf{F}\times \mathbf R \end{eqnarray}$
将其中的$\mathbf{F}$以式(5)代入,令$J=J_{0}+mR^{2}$,导出矢量方程(6)在$Oy$轴上的投影式
(7) $\begin{eqnarray} \left( {J+mRl} \right)\ddot{{\theta }}-mgR\theta +J\dot{{\varOmega }}=M_{{c}} \end{eqnarray}$
为讨论系统$\left\{ B \right\}$的运动,设$B_{{\ast}} $对$\left({O_{c} -xyz} \right)$各轴的主惯量矩为$A$, $B$, $C$,则$\left\{ B \right\}$对$O_{c}$点的动量矩为$\mathbf{L}=A\dot{{\psi }}\mathbf i+\left( {B\dot{{\theta}}+J_{0} \varOmega } \right)\mathbf j+C\dot{{\varphi}}\mathbf k$。列写$\left\{ B \right\}$对质心$O_{c}$的动量矩定理时,控制力矩$\mathbf{M}_{c}$是系统的内力矩而不再出现,重力$m\mathbf{g}$因作用点与矩心重合也不出现,仅有的外力矩来自地面约束力$\mathbf{F}$。以$\left({O_{c} -xyz} \right)$为参考坐标系,列出
(8) $\begin{eqnarray} \frac{\tilde{\rm d}\mathbf{L}}{{\rm d}t}+\mathbf \omega\times\mathbf{L}=\mathbf{F}\times \left( {\mathbf{R+l}} \right) \end{eqnarray}$
将式(8)中的$\mathbf{F}$以式(5)代入,向$\left( {O_{c} -xyz}\right)$各轴投影,得到
(9a) $\left[ {A+m\left( {R+l} \right)^{2}} \right]\ddot{{\psi }}-\left({J+mRl} \right)\varOmega \dot{{\varphi }}-\left( {R+l} \right)mg\psi =0$
(9b) $\left[ {B+m\left( {R+l} \right)^{2}} \right]\ddot{{\theta }}+\left({J+mRl} \right)\dot{{\varOmega }}-\left( {R+l} \right)mg\theta =0$
(9c) $C\ddot{{\varphi }}+J_{0} \varOmega \dot{{\psi }}=0$
若不加控制,令式(9b)中$\dot{{\varOmega }}=0$,则成为倒置的复摆方程,$\theta=0$为不稳定的直立状态。若施加控制,采用与$\theta $成比例的最简单的控制方案
(10) $\begin{eqnarray} M_{c} =k\theta \end{eqnarray}$
(11) $\begin{eqnarray} J\dot{{\varOmega }}=\left( {k+mgR} \right)\theta -\left( {J+mRl}\right)\ddot{{\theta }} \end{eqnarray}$
从式(9b)和式(11)消去$\dot{{\varOmega }}$,引入$\alpha ={{mRl}/J}$,得到
(12) $\begin{eqnarray} \left[ {B+m\left( {R+l} \right)^{2}-\left( {1+\alpha } \right)\left( {J+mRl} \right)} \right]\ddot{{\theta }}+\left[ {k\left( {1+\alpha } \right)-mg\left( {l-\alpha R} \right)} \right]\theta =0 \end{eqnarray}$
将车轮视为均质圆盘,令$J_{0} ={{m_{1} R^{2}}/2}$,则$J=m_{\ast } R^{2}$,$m_{\ast } =m+\left( {{{m_{1} }/2}}\right)$,引入$\alpha ={ml}/({m_{\ast} R})$。将式(12)中$\ddot{{\theta}}$的系数中带负号部分化作
(13) $\begin{eqnarray} \left( {1+\alpha } \right)\left( {J+mRl} \right)=\frac{1}{m_{\ast }}\left( {m_{\ast }R+ml} \right)^{2} \end{eqnarray}$
因$m>>m_{1} $,$m_{\ast }$与$m$接近,若将式(13)右项的分子和分母中的$m_{\ast }$均以$m$近似代替,则化作$m\left( {R+l}\right)^{2}$。可推知式(12)中$\ddot{{\theta}}$的系数近似等于$B$。方程(12)的特征方程为
(14) $\begin{eqnarray} B\lambda^{2}+\left[ {k\left( {1+\alpha } \right)-mg\left( {l-\alpha R} \right)} \right]\theta =0 \end{eqnarray}$
(15) $\begin{eqnarray} k>mg\left( {\frac{l-\alpha R}{1+\alpha }} \right) \end{eqnarray}$
则特征根为纯虚数,$\theta=0$为稳定平衡,证明骑手的直立状态对前后侧扰动保持稳定。但根据运动稳定性的一次近似理论,线性系统的特征根实部为零属于临界情形,只能判定线性系统的零解稳定,而不能判断未经线性化的原系统的稳定性[5 ] 。
为提高控制过程的灵敏性和稳定性,可在简单控制规律(10)中增加随$\dot{{\theta}}$变化的因素,变为
(16) $\begin{eqnarray} M_{c} =k\theta +k_{1} \dot{{\theta }} \end{eqnarray}$
则方程(12)中应增加一项$k_{1} \left( {1+\alpha } \right)\dot{{\theta}}$,特征方程变为
(17) $\begin{eqnarray} &&B\lambda^{2}+k_{1} \left( {1+\alpha } \right)\lambda +\big[ k\left( {1+\alpha } \right)-\\&&\qquad mg\left( {l-\alpha R} \right) \big]\theta =0 \end{eqnarray}$
因特征根的实部均为负数,根据李雅普诺夫一次近似稳定性理论,此线性系统的零解变为渐近稳定,且能判定原系统的零解亦渐近稳定。
对滑板车变向和转弯的解释须利用方程(9a)和(9c)。设车轮转速在转弯过程中维持常值$\varOmega_{0} $不变。当骑手开始向右侧倾斜时,尚未变向的车体仍维持短暂的$\dot{{\varphi}}=0$。方程(9a)成为以$\psi$为变量的倒置复摆的动力学方程。重力导致的倾覆角加速度$\ddot{{\psi}}$从零开始按指数规律增长。当增长至有角速度$\dot{{\psi}}$出现时,引起车轮的动量矩矢量$\mathbf{L}_{1}$进动,产生陀螺力矩$J\varOmega_{0} \dot{{\psi}}$。依据方程(9c),车体出现绕$z$轴的角加速度$\ddot{{\varphi}}$,使前进方向发生改变趋势。所产生的惯性力矩$C\ddot{{\varphi}}$与车轮的陀螺力矩平衡。当角加速度$\ddot{{\varphi }}$随时间积累到有$\varphi$角出现时,转弯过程完成,直线运动变为曲线运动。所产生的离心惯性力推动骑手恢复原位,保证了骑手在侧向平面内的站立稳定性。
为分析此稳定过程,令方程(9a)和(9c)中$\varOmega =\varOmega_{0} $,将$\psi$和$\varphi $视为扰动量,导出此线性方程组的特征方程
(18) $\begin{eqnarray} \lambda^{2}\left( {a\lambda^{2}+b} \right)=0 \end{eqnarray}$
(19) $\begin{eqnarray} \left.\begin{array}{l} a=C\left[ {A+m\left( {R+l} \right)^{2}} \right]\\ b=J_{0} \left[{J_{0} +mR\left( {R+l} \right)} \right]\varOmega_{0}^{2} -Cmg\left( {R+l} \right) \end{array}\right\} \end{eqnarray}$
在方程(18)确定的特征值中,$\lambda =0$的零特征值体现了变量$\varphi$因无恢复力导致的随遇性。另两个特征值的纯虚根条件为$b>0$,即$\psi$和$\varphi $耦合运动的零解稳定性条件。从中导出车轮的最低转速
(20) $\begin{eqnarray} \varOmega_{{0,\min}} =\sqrt {\frac{Cmg\left( {R+l} \right)}{J_{0} \left[ {J_{0} +mR\left( {R+l} \right)} \right]}} \end{eqnarray}$
只要使车轮转速满足$\varOmega_{0} >\varOmega_{{0,\min}}$,骑手对左右侧扰动的站立稳定性就能得到保证。
与前文对前后侧扰动的稳定性分析类似,线性系统的零解稳定不能判断原系统的稳定性。但实际上任何机械系统均难以避免阻尼因素,若在系统中增加与角速度$\dot{{\psi}}$成比例的阻尼项,则线性系统的零解即转为渐近稳定。根据李雅普诺夫一次近似稳定性理论,未经线性化的原系统的零解亦渐近稳定。
以上对滑板车运动过程的分析表明,骑手的肢体动作或控制电机的驱动制动,最终均转化为重力和地面摩擦力对车体和骑手的作用。滑板车运动状态的改变是重力和地面摩擦力的作用结果。任何系统都不可能依靠内力改变运动状态。
参考文献
View Option
[1]
刘延柱 . 动力滑板车漫话
力学与实践 , 2009 , 31 (6 ): 95 -96
[本文引用: 1]
Liu Yanzhu . Talk on segway human transporter
Mechanics in Engineering 2009 , 31 (6 ): 95 -96 (in Chinese)
[本文引用: 1]
[2]
刘延柱 . 缩小的赛格威车——谈自平衡滑板
力学与实践 , 2017 , 39 (2 ): 208 -210
[本文引用: 1]
Liu Yanzhu . A miniature segway-talk on self-balancing scooter
Mechanics in Engineering 2017 , 39 (2 ): 208 -210 (in Chinese)
[本文引用: 1]
[3]
Onewheel: 独轮电动滑板让你纵横驰骋 , https://www.ifanr.com/354598
URL
[本文引用: 1]
[4]
刘延柱 . 关于自行车的稳定性
力学与实践 , 2012 , 34 (2 ): 90 -93
[本文引用: 1]
Liu Yanzhu . On the stability of bicycle
Mechanics in Engineering 2012 , 34 (2 ): 90 -93 (in Chinese)
[本文引用: 1]
[5]
刘延柱 . 高等动力学, 第2版 . 北京 : 高等教育出版社 , 2016
[本文引用: 1]
动力滑板车漫话
1
2009
... 自2008年北京奥运会上自平衡的赛格威车首次亮相以来[1 ] ,2015年出现了赛格威车缩小版的自平衡双轮滑板车[2 ] .与此同时,又有构造更简单的称为"Onewheel"的自平衡独轮滑板车问世 (图1 )[3 ] .这种新型的代步工具只有一个轮子,仅依靠驾车人的身体动作就能实现加速、减速和转弯等各种功能.虽然操纵难度比双轮滑板车更大,需要掌握更多技巧才能熟练驾驶,但骑手能感受到自由飞翔般地飘浮感觉,因而备受年轻人的青睐.各种新设计和产品不断涌现,促使自平衡滑板车的技术和产业在国内快速发展. ...
动力滑板车漫话
1
2009
... 自2008年北京奥运会上自平衡的赛格威车首次亮相以来[1 ] ,2015年出现了赛格威车缩小版的自平衡双轮滑板车[2 ] .与此同时,又有构造更简单的称为"Onewheel"的自平衡独轮滑板车问世 (图1 )[3 ] .这种新型的代步工具只有一个轮子,仅依靠驾车人的身体动作就能实现加速、减速和转弯等各种功能.虽然操纵难度比双轮滑板车更大,需要掌握更多技巧才能熟练驾驶,但骑手能感受到自由飞翔般地飘浮感觉,因而备受年轻人的青睐.各种新设计和产品不断涌现,促使自平衡滑板车的技术和产业在国内快速发展. ...
缩小的赛格威车——谈自平衡滑板
1
2017
... 自2008年北京奥运会上自平衡的赛格威车首次亮相以来[1 ] ,2015年出现了赛格威车缩小版的自平衡双轮滑板车[2 ] .与此同时,又有构造更简单的称为"Onewheel"的自平衡独轮滑板车问世 (图1 )[3 ] .这种新型的代步工具只有一个轮子,仅依靠驾车人的身体动作就能实现加速、减速和转弯等各种功能.虽然操纵难度比双轮滑板车更大,需要掌握更多技巧才能熟练驾驶,但骑手能感受到自由飞翔般地飘浮感觉,因而备受年轻人的青睐.各种新设计和产品不断涌现,促使自平衡滑板车的技术和产业在国内快速发展. ...
缩小的赛格威车——谈自平衡滑板
1
2017
... 自2008年北京奥运会上自平衡的赛格威车首次亮相以来[1 ] ,2015年出现了赛格威车缩小版的自平衡双轮滑板车[2 ] .与此同时,又有构造更简单的称为"Onewheel"的自平衡独轮滑板车问世 (图1 )[3 ] .这种新型的代步工具只有一个轮子,仅依靠驾车人的身体动作就能实现加速、减速和转弯等各种功能.虽然操纵难度比双轮滑板车更大,需要掌握更多技巧才能熟练驾驶,但骑手能感受到自由飞翔般地飘浮感觉,因而备受年轻人的青睐.各种新设计和产品不断涌现,促使自平衡滑板车的技术和产业在国内快速发展. ...
1
... 自2008年北京奥运会上自平衡的赛格威车首次亮相以来[1 ] ,2015年出现了赛格威车缩小版的自平衡双轮滑板车[2 ] .与此同时,又有构造更简单的称为"Onewheel"的自平衡独轮滑板车问世 (图1 )[3 ] .这种新型的代步工具只有一个轮子,仅依靠驾车人的身体动作就能实现加速、减速和转弯等各种功能.虽然操纵难度比双轮滑板车更大,需要掌握更多技巧才能熟练驾驶,但骑手能感受到自由飞翔般地飘浮感觉,因而备受年轻人的青睐.各种新设计和产品不断涌现,促使自平衡滑板车的技术和产业在国内快速发展. ...
关于自行车的稳定性
1
2012
... 需要转弯时,与驾驭滑雪板或冲浪板的方法类似,驾车人带动车体向要转弯的一侧倾斜.利用与自行车类似的"离心力效应" 和"陀螺效应",倾斜车体的重力与支承力构成力偶,使旋转中的车轮进动,出现绕垂直轴的转动.由此产生的陀螺力矩与重力矩平衡[4 ] .车体绕垂直轴的转动使直线轨道发生偏转,从而实现转弯动作.沿曲线轨道行进的车体和人体产生离心惯性力,使驾车人恢复直立姿态避免摔倒.独轮滑板车厚重车轮的动量矩明显大于自行车的前轮,陀螺效应也更为明显. ...
关于自行车的稳定性
1
2012
... 需要转弯时,与驾驭滑雪板或冲浪板的方法类似,驾车人带动车体向要转弯的一侧倾斜.利用与自行车类似的"离心力效应" 和"陀螺效应",倾斜车体的重力与支承力构成力偶,使旋转中的车轮进动,出现绕垂直轴的转动.由此产生的陀螺力矩与重力矩平衡[4 ] .车体绕垂直轴的转动使直线轨道发生偏转,从而实现转弯动作.沿曲线轨道行进的车体和人体产生离心惯性力,使驾车人恢复直立姿态避免摔倒.独轮滑板车厚重车轮的动量矩明显大于自行车的前轮,陀螺效应也更为明显. ...
1
2016
... 则特征根为纯虚数,$\theta=0$为稳定平衡,证明骑手的直立状态对前后侧扰动保持稳定.但根据运动稳定性的一次近似理论,线性系统的特征根实部为零属于临界情形,只能判定线性系统的零解稳定,而不能判断未经线性化的原系统的稳定性[5 ] . ...