力学与实践, 2021, 43(5): 801-805 DOI: 10.6052/1000-0879-20-310

力学纵横:身边力学的趣话

由一张A4纸引发的思考1)

黄可*, 郭昱均*, 郝泱*, 李栋栋,*,2), 范钦珊*,†

*南京航空航天大学,南京 210016

†清华大学航天航空学院工程力学系,北京100084

INSPIRATION OF A SHEET OF A4 PAPER1)

HUANG Ke*, GUO Yujun*, HAO Yang*, LI Dongdong,*,2), FAN Qinshan*,†

*Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

†Department of Engineering Mechanics, School of Aerospace Engineering, Tsinghua University, Beijing 100084, China

通讯作者: 2)李栋栋,讲师,主要研究方向为梯度多孔夹层结构的力学行为分析及优化。E-mail:lidongdong@nuaa.edu.cn

责任编辑: 胡漫

收稿日期: 2020-07-30   修回日期: 2020-08-27  

基金资助: 1)江苏高校优势学科建设工程资助项目

Received: 2020-07-30   Revised: 2020-08-27  

作者简介 About authors

摘要

为了从力学角度解释"一张打印纸平着立不起来,而弯曲一定弧度后就可以"这一现象,本文通过数学手段对两种状态下横截面几何性质进行演算,得到了截面形心主惯性矩的计算公式,并结合计算机分析进行验证,证明了公式的适用性。通过对纸张稳定性的讨论,把该问题抽象为自重状态下的压杆稳定性分析,发现弯曲弧度对于稳定性影响很大,当弧度为2.52时,圆柱面状A4纸均布轴向载荷的临界值约为平面状A4纸的$3.7\times 10^{5}$倍。

关键词： 打印纸; 惯性矩; 稳定性分析

Abstract

In order to explain the phenomenon that "a sheet of printing paper cannot be erected, while a certain degree curved one can" in terms of mechanics, the geometric properties of the cross section under two different states are analyzed to form a formula for the principal centroidal moments of inertia, which is verified by numerical simulations. The stability of the sheet of paper or a curved one is reduced into the stability of a column under its own weight. It is found that the curvature of the arc has a great influence on the stability. When the arc is 2.52, the critical value of the evenly distributed axial load of the cylindrical A4 paper is about $3.7\times10^5$ times of that of the planar one.

Keywords： printing paper; moment of inertia; stability analysis

PDF (274KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

黄可, 郭昱均, 郝泱, 李栋栋, 范钦珊. 由一张A4纸引发的思考1). 力学与实践, 2021, 43(5): 801-805 DOI:10.6052/1000-0879-20-310

HUANG Ke, GUO Yujun, HAO Yang, LI Dongdong, FAN Qinshan. INSPIRATION OF A SHEET OF A4 PAPER1). MECHANICS IN ENGINEERING, 2021, 43(5): 801-805 DOI:10.6052/1000-0879-20-310

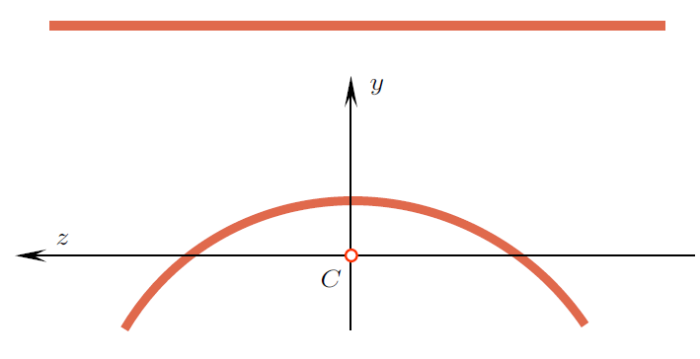
范钦珊等[1]在材料力学课上,通过"一张打印纸的思考"提出了一个深度研讨问题："为什么一张打印纸平着立不起来,而弯曲一定的弧度后就可以立起来?"如图1所示,这一问题引发了同学们的广泛讨论。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   深度研讨问题


A4打印纸(以下简称A4纸)是生活中十分常见的物品,在很多中小学生的趣味活动中,也有将A4纸立起来的项目。虽然说将A4纸弯曲就能将其立起来是一件非常容易的事情,但是这背后的力学知识可不简单。

立起来的A4纸可能会因$y$轴方向的扰动力而绕$z$轴发生失稳。由于截面弯曲刚度定义为$EI$,其中$E$为材料的杨氏模量,$I$为横截面的惯性矩,而截面弯曲刚度体现了A4纸抵抗弯曲变形及抵抗失稳的能力,故本文以A4纸在不同状态下的横截面的形心主惯性矩为切入点,并从稳定性的角度深入地分析这个问题。

1 截面几何性质的理论计算

本文的研究对象为平面状和弯曲形状A4纸,而对于弯曲形状A4纸,只研究其圆柱面状,其他弯曲形状可以使用类似的方法得到相应的结果。

1.1 平面状A4纸

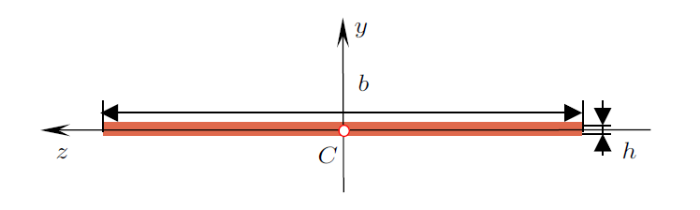
记纸张的宽度$b = 210$ mm,高度$l = 297$ mm,厚度$h = 0.1$ mm。

对于平面状A4纸,形心位于对角线的交点,横截面的两个对称轴即为形心主惯性轴,记为$y$和$z$轴,以形心为坐标原点建立$yCz$坐标系(图2)。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   平面状A4纸的横截面


根据惯性矩的定义[2],可以得到惯性矩的计算公式

$\left. {\begin{array}{l} I_{z} =\int_A {y^{2}{\rm d}A} \\ I_{y} =\int_A {z^{2}{\rm d}A} \\ \end{array}} \right\}$

由于平面状A4纸的横截面为矩形,由矩形截面对$z$和$y$轴的形心主轴惯性矩公式[2]可得

$\left. {\begin{array}{l} I_{z} =\dfrac{bh^{3}}{12} \\ I_{y} =\dfrac{hb^{3}}{12} \\ \end{array}} \right\}$

1.2 圆柱面状A4纸

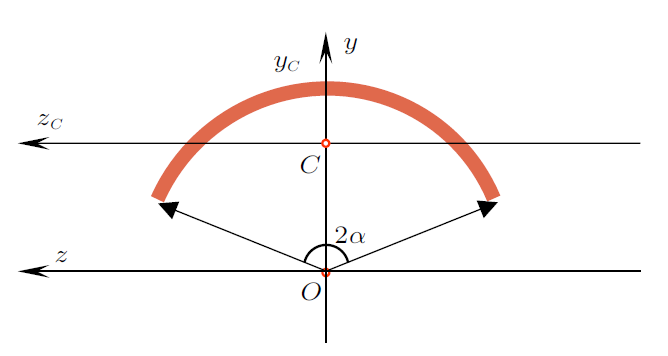
对于弯曲的状态,纸张在弯曲后形成圆柱面,圆心角为2$\alpha$,中心轴的圆弧曲率半径为$\rho $。$\alpha $与$\rho $之间关系为

$\rho =\dfrac{b}{2\alpha }$

以圆心为坐标原点建立$yOz$坐标系,以形心为坐标原点建立$y_{C} Cz_{C} $坐标系,如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   圆柱面状A4纸的横截面


首先根据形心计算公式可得

$\left. {\begin{array}{l} z_{C} =\dfrac{\int_A {z{\rm d}A} }{A} \\ y_{C} =\dfrac{\int_A {y{\rm d}A} }{A} \\ \end{array}} \right\}$

对坐标进行极坐标变换

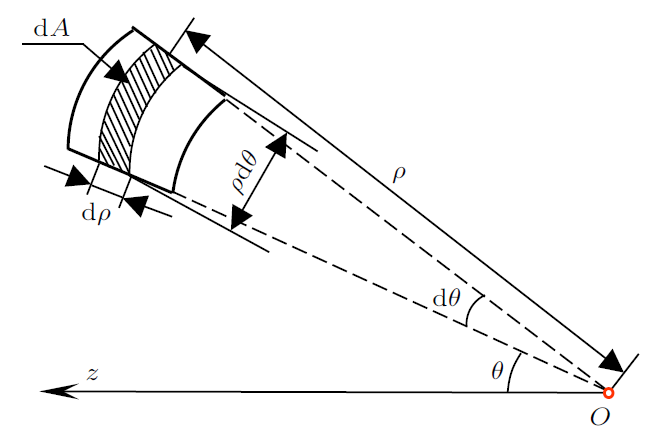
$\left. {\begin{array}{l} z=\rho \cos \theta \\ y=\rho \sin \theta \\ \end{array}} \right\}$

由图4可知

${\rm d}A=\rho {\rm d}\theta {\rm d}\rho$

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   积分变量代换示意图


由式(4) $\sim\!$式(6)得

$\left. {\begin{array}{l} z_{C} =0 \\ y_{C} =\dfrac{\int_{{\pi}/{2}-\alpha }^{{\pi}/{2}+\alpha }{\int_{\rho -{h}/{2}}^{\rho +{h}/{2}} {(\rho \sin \theta )\rho{\rm d}\theta {\rm d}\rho } } }{hb}=\\[3mm]\qquad \dfrac{2\sin \alpha }{b}\left( {\rho^{2}+\dfrac{1}{12}h^{2}} \right) \\ \end{array}} \right\}$

记

$a=y_{C} =\dfrac{2\sin \alpha }{b}\left( {\rho^{2}+\dfrac{1}{12}h^{2}}\right)$

由式(1)得图形对于$z$轴和$y$轴的惯性矩

$\left. {\begin{array}{l} I_{z} =\left( {\alpha +\dfrac{1}{2}\sin 2\alpha } \right)\left( {\rho^{3}h+\dfrac{1}{4}\rho h^{3}} \right) \\ I_{y} =\left( {\alpha -\dfrac{1}{2}\sin 2\alpha } \right)\left( {\rho^{3}h+\dfrac{1}{4}\rho h^{3}} \right) \\ \end{array}} \right\}$

由移轴定理[2]可以求出圆柱面状A4纸横截面的形心主惯性矩

$\left. {\begin{array}{l} I_{z_{C} } =I_{z} -a^{2}A \\ I_{y_{C} } =I_{y} \\ \end{array}} \right\}$

将式(3)、式(8)、式(9)代入式(10),整理得

$\left. {\begin{array}{l} I_{z_{C} } =\left( {\alpha +\dfrac{1}{2}\sin 2\alpha } \right)\left({\dfrac{b^{3}h}{8\alpha^{3}}+\dfrac{bh^{3}}{8\alpha }} \right)-\\[3mm]\qquad \dfrac{h\sin^{2}\alpha }{4b}\left( {\dfrac{b^{2}}{\alpha^{2}}+\dfrac{1}{3}h^{2}}\right)^{2} \\ I_{y_{C} } =\left( {\alpha -\dfrac{1}{2}\sin 2\alpha } \right)\left({\dfrac{b^{3}h}{8\alpha^{3}}+\dfrac{bh^{3}}{8\alpha }} \right) \\ \end{array}} \right\}$

2 计算机仿真模拟与验证

对于圆柱面状A4纸利用SolidWorks中的截面分析,当曲率半径$\rho = 83.4$ mm ($\alpha = 1.26$ rad)时,可以得到

$I_{z_{C}} =6 466.79~{\rm mm}^{4},\ \ I_{y_{C}} =55 934.93~{\rm mm}^{4}$

将截面的曲率半径$\rho = 83.4$ mm,$b = 210$ mm,$h = 0.1$ mm代入式(3)、式(11)且忽略高阶项可以得到

$\left. {\begin{array}{l} I_{z_{C} } =\rho^{3}h\left( {\dfrac{b}{2\rho }+\dfrac{1}{2}\sin\dfrac{b}{\rho }} \right)-\\[3mm]\qquad \dfrac{4h\rho^{4}\sin^{2}\left( {{b/{2\rho }}}\right)}{b}=6 491.68~ {\rm mm}^{4} \\[2mm] I_{y_{C} } =\rho^{3}h\left( {\dfrac{b}{2\rho }-\dfrac{1}{2}\sin\dfrac{b}{\rho }} \right)=56 095.60~{\rm mm}^{4} \\ \end{array}} \right\}$

式(12)与式(13)的结果基本一致,由此可以验证式(11)的正确性。

当$\rho \to \infty $时,由式(3)得$\alpha \to 0$,可以得到

$\left. {\begin{array}{l} I_{z_{C} } \to \dfrac{bh^{3}}{12} \\[1.5mm] I_{y_{C} } \to \dfrac{hb^{3}}{12} \\ \end{array}} \right\}$

由式(14)可以看出,推导出的结果具有一般性。

将式(13)中$I_{z_{C} } $与$I_{y_{C} } $的表达式相减得

$I_{z_{C} } -I_{y_{C} } =\frac{2\rho^{3}h\sin [b/(2\rho)]}{b}\cdot \ \left( {b\cos [b/(2\rho)]-2\rho \sin [b/(2\rho)]}\right)$

在定义域${b}/(2\pi)\leqslant \rho <+\infty $内,式(15)恒小于或等于零,所以$I_{z_{C}} \leqslant I_{y_{C}} $,当且仅当$\rho =b/(2\pi)$时, $I_{z_{C}} =I_{y_{C} }$。故圆柱面状A4纸容易绕着$z$轴发生失稳。

3 两种不同初始形状A4纸截面惯性矩的对比

截面的不同导致A4纸抵抗屈曲失稳的能力不同。从截面弯曲刚度的定义$EI$可以看出：对于同种材料,在其他条件保持不变的前提下,截面的惯性矩越大,弯曲刚度就越大,它抵抗弯曲变形及抵抗失稳的能力就会越强。

A4纸抵抗绕$z$轴发生失稳的能力,与截面对于$z$轴的形心主惯性矩有直接关系。由上面的计算我们可以看到：当曲率半径$\rho = 83.4$ mm时,圆柱面状A4纸截面对于$z$轴的形心主惯性矩$I_{z_{C}} =6 491.68$ mm$^{4}$,而平面状A4纸截面对于$z$轴的形心主惯性矩$I_{z_{C}} =0.017 5$ mm$^{4}$。前者约为后者的$3.7\times10^{5}$倍,也就是说圆柱面状A4纸抵抗绕$z$轴发生失稳的能力远远强于平面状A4纸。

4 对于形心主惯性矩极值的探讨

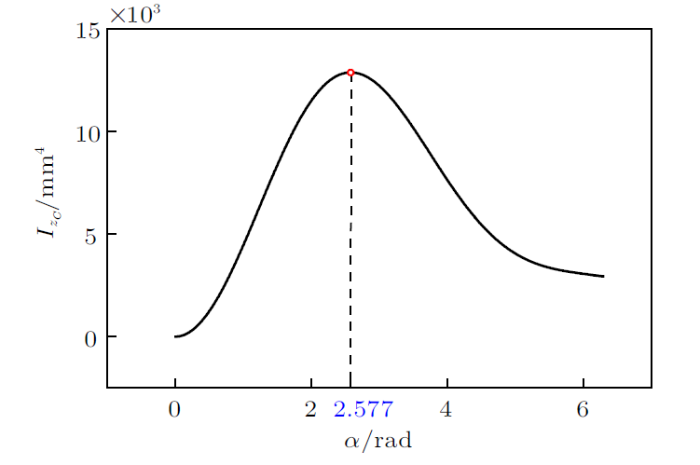
由上面的分析可以得出,对于$z$轴惯性矩的增大是圆柱面状A4纸能直立起来的主要原因。通过计算得到$I_{z_{C}}$最大时对应纸张弯曲的程度,进而得出最不容易翻倒的状态。

由式(11),有

$I_{z_{C} } =\left( {\alpha +\dfrac{1}{2}\sin 2\alpha } \right)\left({\dfrac{b^{3}h}{8\alpha^{3}}+\dfrac{bh^{3}}{8\alpha }} \right)-\ \frac{h\sin^{2}\alpha }{4b}\left( {\dfrac{b^{2}}{\alpha^{2}}+\frac{1}{3}h^{2}}\right)^{2}$

利用数值求解方法可得：当截面圆弧圆心角的一半$\alpha = 2.577$ rad时,$I_{z_{C}}$取到最大值。该函数图像如图5。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   $I_{z_{C}}$随着$\alpha $的变化趋势


5 对于此问题本质的讨论

5.1 本质的分析

本文所讨论的A4纸问题实际上可以抽象为自重状态下的压杆稳定问题,现建立该问题的力学模型。

5.2 利用能量法确定均布轴向载荷的临界值

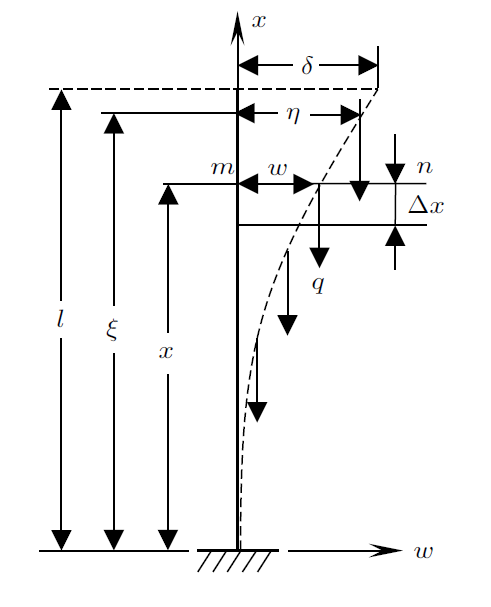
将纸张等效为下端固定、上端自由、承受均布轴向载荷的杆件,如图6所示,图中的虚线即为屈曲后的杆件。$l$为压杆长度,$x$为$mn$截面到固定端竖直方向的距离, $\Delta(x)$为杆件屈曲时$mn$截面沿竖直方向移动的距离,$w$为$mn$截面处的挠度,$\delta$为自由端的挠度,$\xi $为所研究微段到固定端竖直方向的距离,$\eta$为所研究微段处的挠度,$q$为自重均布轴向载荷,其临界值记为$q_{\rm cr}$。设挠度曲线函数为

$w\left( x \right)=a_{1} \left( {1-\cos \dfrac{\pi x}{2l}} \right)$

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   自重压杆的示意图


从直线平衡构形转变为弯曲平衡构形,系统的总势能改变量为

$\varDelta V_{{\rm t}} =V_{{\rm P}} +V_{\varepsilon}$

其中位置势能$V_{{\rm P}}$和应变能$V_{\varepsilon}$分别为

$\left. {\begin{array}{l} V_{{\rm P}} =-\int_l { {q{\rm d}x} } \varDelta \left( x \right) \\[3mm] V_{\varepsilon} =\int_0^l {\dfrac{M^{2}}{2EI}} {\rm d}x \\ \end{array}} \right\}$

利用小变形及泰勒展开,式(19)中

$\varDelta \left( x \right)=\int_0^x {\left({{\rm d}x-{\rm d}x\cos \theta } \right)} =\int_0^x {\left( {1-\cos \theta } \right)}{\rm d}x=\ \ \frac{1}{2}\int_0^x {\left( {\frac{{\rm d}w}{{\rm d}x}} \right)}^{2}{\rm d}x$

将式(17)代入式(20)后积分,有

$\varDelta \left( x \right)=\frac{1}{2}\int_0^x{\left( {\frac{{\rm d}w}{{\rm d}x}} \right)}^{2}{\rm d}x=\ \ \frac{1}{2}\left( {\frac{\pi }{2l}} \right)^{2}a_{1}^{2}\left( {-\frac{l}{\pi }\sin \frac{\pi x}{2l}\cos \dfrac{\pi x}{2l}+\frac{x}{2}} \right)$

将式(21)代入式(19),得到位置势能

$V_{{\rm P}} =-\int_0^l {{q{\rm d}x} \varDelta \left( x \right)} =-q\dfrac{\pi^{2}}{32}a_{1}^{2} \times \dfrac{\pi ^{2}-4}{\pi^{2}}$

在任意截面$mn$的弯矩为

$M=\int_x^l q (\eta -w){\rm d}\xi$

并注意

$\eta =a_{1} \left( {1-\cos \dfrac{\pi \xi }{2l}} \right)$

得到

$M=a_{1} q\left[ {(l-x)\cos \dfrac{\pi x}{2l}-\dfrac{2l}{\pi }\left( {1-\sin \dfrac{\pi x}{2l}} \right)} \right]$

将式(25)代入式(19),得到应变能

$V_{\varepsilon} =\int_0^l {\dfrac{M^{2}}{2EI}} {\rm d}x=\dfrac{a_{1}^{2}q^{2}l^{3}}{2EI}\left( {\dfrac{1}{6}+\dfrac{9}{\pi^{2}}-\dfrac{32}{\pi ^{3}}} \right)$

将式(22)、式(26)代入式(18),并令其等于零,最后得到均布轴向载荷的临界值

$q_{\rm cr} =\dfrac{7.89EI}{l^{3}}$

而文献[3]中用贝塞尔函数法得到的精确解为

$q_{\rm cr1} =\dfrac{7.837EI}{l^{3}}$

通过对比可以发现：本文方法利用更为简洁的推导得到了与文献[3]精度相当的结果。

此外,在其他条件相同的情况下,自重均布轴向载荷临界值$q_{\rm cr}$与$I$成正比,临界值的比值即为惯性矩的比值。当曲率半径$\rho = 83.4$ mm时,圆柱面状A4纸截面对于$z$轴的形心主惯性矩约为平面状A4纸截面的$3.7\times 10^{5}$倍,故圆柱面状A4纸均布轴向载荷的临界值同样约为平面状A4纸的$3.7\times 10^{5}$倍。

6 对于纸张稳定性的定量分析

由于现有文献中,关于A4纸杨氏模量的报道较少,本文拟采用文献[4]中克重$k$为45 g/m$^{2}$、湿度为6%时,低克重卷筒票据印刷纸杨氏模量的数值进行相关的定量计算,即$E=1.271$ GPa。

6.1 纸张在两种状态下的稳定性分析

对于平面状A4纸,将$I_{z} =0.017 5$ mm$^{4}$代入式(28)可得

$q_{\rm cr} =\dfrac{7.837EI}{l^{3}}=6.654\times 10^{-3}~{\rm N/m}$

纸张的均布轴向载荷$q_{纸}$为

$q_{纸} =9.8kb=0.093 {\rm N/m} \gg q_{\rm cr}$

由于其临界屈曲载荷远小于纸张所受的均布载荷,所以平面状A4纸在自重作用下很容易发生屈曲失稳。

对于圆柱面状A4纸,当$\rho= 83.4$ mm时,将$I_{z_{C} } =6 491.68$ mm$^{4}$代入式(28)可得

$q_{\rm cr} =\dfrac{7.837EI}{l^{3}}=2 468.22~\mbox{N/m}\gg q_{纸}$

由于其临界屈曲载荷远大于纸张所受的均布载荷,所以该数值算例中的圆柱面状A4纸在自重状态下不会发生屈曲失稳。

6.2 对于圆柱面状A4纸在自重作用下发生屈曲的临界弧度

在自重作用下,由式(28)可得

$I_{z} =\dfrac{q_{纸}l^{3}}{7.837E}=2.568 9\times 10^{-4}~{\rm mm}^{4}$

令式(11)和式(32)相等,再通过二分法求解可得此时曲率半径为

$\rho_{\rm cr} =1 485 964.35~{\rm mm}$

由式(3)可得临界弯曲弧度为

$\theta_{\rm cr} =2\alpha =\dfrac{b}{\rho_{\rm cr} }=1.413\times 10^{-4}~{\rm rad}$

7 结论

为了解释"一张打印纸平着立不起来,而弯曲一定弧度后就可以"这一现象,本文使用数学方法从截面惯性矩和压杆稳定性两个方面展开讨论,得出如下结论。

(1) 用于推导惯性矩时使用的方法,具有一定的普适性及合理性。

(2) 在$\alpha $的定义域范围内,对于$z$轴的形心主惯性矩随着$\alpha$先增大后减小,且在$\alpha = 2.577$ rad时取得最大值,即在此时圆柱面状A4纸最稳定。

(3)本文给出的均布轴向载荷临界值的表达式精度较高,满足一般的工程需求,且推导过程简洁。

(4)平面状A4纸立不起来,其力学本质是自重状态下发生了失稳,而圆柱面状A4纸能够立起来,是因为截面形状的改变使得形心主惯性矩显著增加,从而增强了A4纸抵抗失稳的能力。

参考文献

范钦珊, 殷雅俊, 唐静静 等 . 改革教学,

创新教学——"材料力学" 课程教学改革实践与体会

力学与实践, 2018, 40(5):543-549

[本文引用: 1]

Fan Qinshan, Yin Yajun, Tang Jingjing, et al.

Reform and innovation, a decade practice of improvement of the course of the strength of materials

Mechanics in Engineering, 2018, 40(5):543-549 (in Chinese)

[本文引用: 1]

殷雅俊, 范钦珊, 王晶 等. 材料力学, 第3版. 北京: 高等教育出版社, 2019

[本文引用: 3]

Yin Yajun, Fan Qinshan, Wang Jing, et al. Mechanics of Materials, 3rd edn. Beijing: Higher Education Press, 2019 (in Chinese)

[本文引用: 3]

Timoshenko SP, Gere JM.

Theory of Elastic Stability, 2nd edn. New York:

McGraw-Hill Book, 1961

[本文引用: 2]

夏自由.

水分对纸张拉伸弹性模量的影响研究

印刷质量与标准化, 2014(9):44-45

[本文引用: 1]

Xia Ziyou.

Research on the influence of moisture on the tensile elastic modulus of paper

Printing Quality and Standardization, 2014(9):44-45 (in Chinese)

[本文引用: 1]

/

〈 〉