材料力学作为工科类学生必修的一门力学基础课程,演绎性较强,其不仅可以为学生进行专业课程学习提供理论基础和基本技能训练,也可以对实验力学、弹性力学、振动力学等其他专业课程学习起到承前启后的作用。因此,将现代光测力学方法用于材料力学实验教学具有重要意义。目前,一些将数字图像相关方法应用在实验教学中的实践^[1-2]仅用了单相机的二维数字图像相关方法,该方法只能测量平面二维变形且应变精度易受离面位移影响。另外,现有的实践中都使用"先采图后处理"的教学方式,还缺少实时的变形测量教学手段和实验教学方法。

本文采用自主研制的实时三维数字图像相关(3D digital image correlation,3D-DIC)教学仪器对铝合金拉伸实验和梁的三点弯实验进行了教学探索,探究了其在材料力学教学中的应用。本文演示的实验有助于培养学生进行受力分析的能力,加深学生对力学概念的理解。同时,实时变形测量易于调动学生的积极性,使得教学过程更加生动活泼。

数字图像相关方法^[3-4]主要利用感兴趣区域内的灰度信息对图像相关性进行匹配,通过测量物体变形前后光强的互相关函数峰值来导出物体的位移^[5],对位移场进行局部差分或者拟合得到应变场。3D-DIC方法结合了数字图像相关方法与立体视觉原理^[6],通过拍摄被测物体变形前后表面形貌特征,跟踪物体表面的散斑图像,通过数字图像相关运算和三维重构来实现物体变形过程中三维位移和表面应变的非接触式全场测量。

由相机成像模型和相机参数可以建立图像中像点与空间中物点的相互位置对应关系,从二维图像中定量提取三维空间被测物体的几何和运动信息。通过实验和计算的方法来确定这些相机参数的过程就是相机标定。

相机坐标系与图像坐标系之间的转换关系为

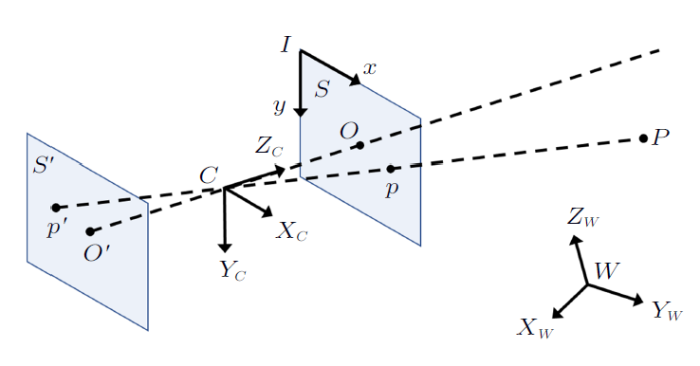
如图1所示,世界坐标系$W$-$X_{W}Y_{W}Z_{W}$,相机坐标系$C$-$X_{C}Y_{C}Z_{C}$,图像坐标系$I$-$xy$。其中,$Z_{C}$是物点到光心的距离在光轴方向的投影,$C_{x}$, $C_{y}$,$F_{x}$, $F_{y}$,$F_{s}$为相机内部参数,组成内参矩阵$ A$。再经平移和旋转可以将世界坐标系和相机坐标系重合,其中旋转矩阵$ R$和平移向量$ T$组成相机外参矩阵。

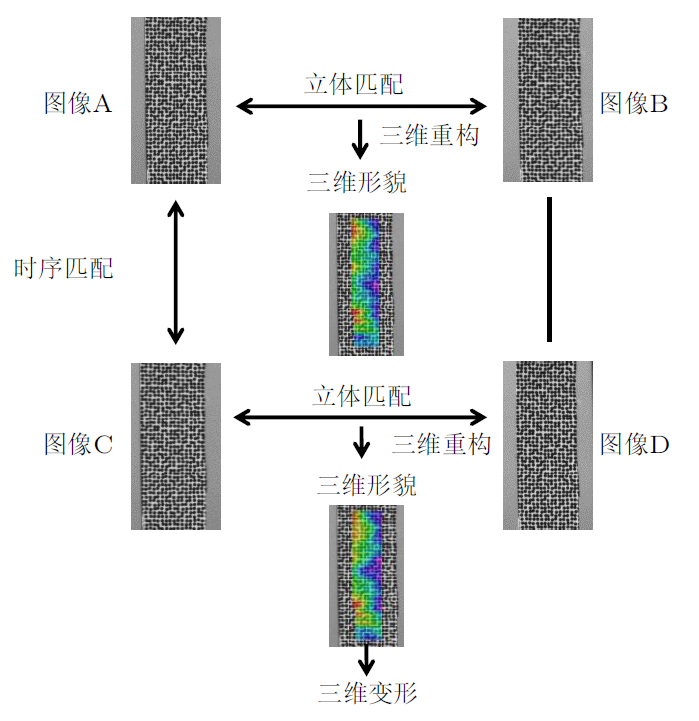
式(1)为单相机的成像示意图,确定空间点的三维坐标信息需要至少两个相机,通过立体视觉来唯一确定空间点的三维坐标信息。其原理与人眼的双目立体感知过程类似,即采用左、右两个相机拍摄同一物体得到不同视角的图像,通过计算分析同一个像点在左右图像中的视差来获取物体表面的三维形貌信息。根据物体变形前后的三维形貌信息即可分析物体表面发生的三维位移和表面应变。

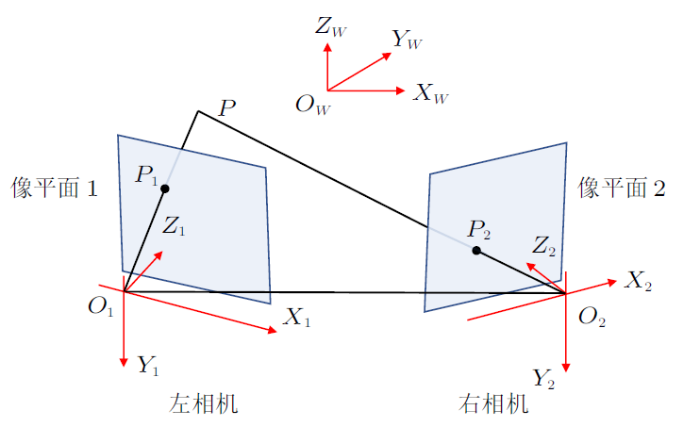
图2为立体视觉模型。$O_{W}$-$X_{W}Y_{W}Z_{W}$为物方世界坐标系,$O_{1}$-$X_{1}Y_{1}Z_{1}$,$O_{2}$-$X_{2}Y_{2}Z_{2}$分别为左、 右相机坐标系,$O$-$XY$为像平面坐标系。点$P(X_{W}$, $Y_{W},Z_{W})$在两相机中对应像点分别为$P_{1}(X_{1},Y_{1},Z_{1})$和$P_{2}(X_{2}$, $Y_{2}, Z_{2})$,直线$O_{1}P_{1}$和$O_{2}P_{2}$相交于点$P$。如果已知$P_{1}$和$P_{2}$的图像坐标和相机内、外参数,就可以利用三角测量原理求得$P$点在物方世界坐标系下的三维坐标。

双相机标定算法的主要流程为：首先采用单相机标定方法对左、右两相机的内参进行标定(相机内参共5个,每幅标定图像可以列出两个方程,因此,需要至少3幅不同姿态的标定图像)。相机外参初值可以通过拍摄多张不同姿态的标定板图像,利用矩阵最小二乘法求解。当内外参数初值确定后对这些参数进行优化,使投影误差最小,优化结束即完成了双相机标定过程。

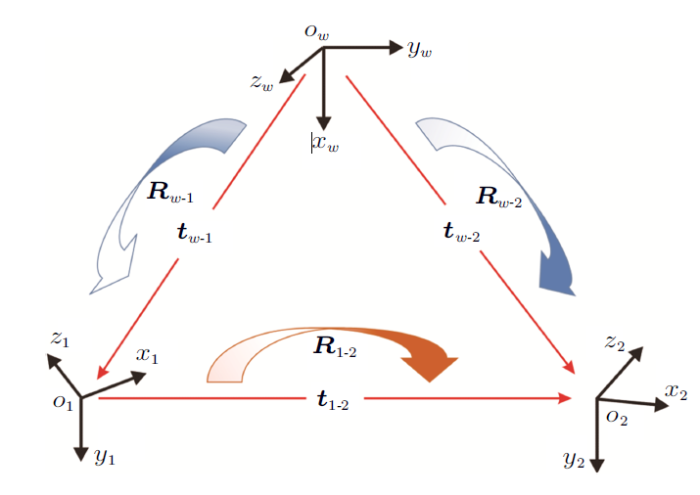
对于每一个相机,已经计算了相机坐标系与世界坐标系之间的相对外参。对于如图3中的两个相机的相对外参,根据坐标变换有

其中的${ T}=\left[ {{\begin{array}{*{20}c} {{ R}} & {{ t}} \\ 0 & 1 \\\end{array} }} \right]$为两个坐标系之间变换矩阵,${ R}$为旋转矩阵,${ t}$为平移向量,$ T_{1\mbox{-}2}$为待求量,而$ T_{w\mbox{-}1}$和$ T_{w\mbox{-}2}$为已知量。

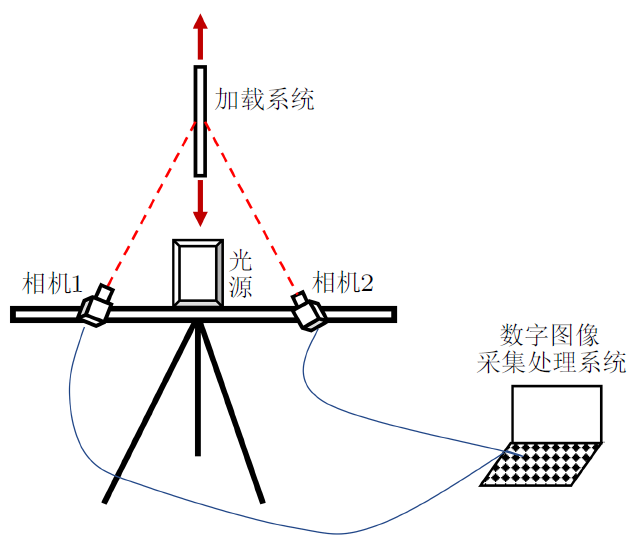
3D-DIC系统的硬件部分主要由相机、光源、三脚架和计算机组成。如图4所示。

根据前述内容,完成立体视觉标定后,得到了相机的内、外参数,建立了图像坐标系和世界坐标系的转换关系,然后通过立体匹配从两个相机图像上对应的像素点二维图像坐标重建出三维空间坐标。三维形貌实质上是由足够多的空间点直接或经过曲面拟合构成的,变形前后的空间点坐标之差即为三维位移,应变场可由对位移场进行局部最小二乘拟合得到。

图5为三维变形计算流程。在计算三维变形过程中有两种图像匹配过程,分别为立体匹配和时序匹配。立体匹配是指匹配同一时刻不同相机的图像子区,完成当前时刻的三维重建。时序匹配是在不同时刻的同一相机图像中匹配图像子区,以实现变形前后的子区跟踪,结合变形前后的三维空间坐标变化便可得到变形信息^[7-8]。

三维数字图像相关变形阶段对每个点的计算包括与左图像匹配、与右图像匹配以及三维重构。在测量区域中,有数千个点需要计算,实时三维数字图像相关软件采用基于种子点扩散和基于CPU的三维多线程并行计算方法^[9]。并行计算可以用于提高三维数字图像相关的计算速度。如图6,种子点的变形被用于给周边点提供改进的初值估计,每一个计算成功的点均被当作一个新的种子点向周边点传递初值。

在实时测量前,需要先架设好测量设备并对测量设备进行三维标定。正式测试前,还需采集参考图像,选择测量区域。同时,参考阶段的三维重构也需要完成。在参考图像采集和三维重构之后可以预先计算坐标变换的参数。在实验过程中,显示器上可以实时显示变形结果。

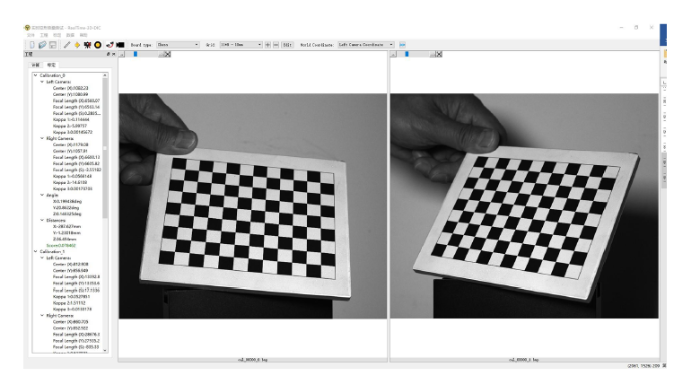
实时3D-DIC计算软件的标定界面如图7所示,界面由工具栏、参数设置栏、状态栏和主界面组成。

工具栏由文件、工程、标定、数据、帮助功能组成。主界面显示导入的标定图,参数设置栏可输入已知的标定板参数,在完成标定图采集后进行标定效果计算。计算完成后,主界面左侧的状态栏会显示各项标定参数的计算结果。

图8所示实时计算界面与标定界面相比,参数设置栏对应的参数为实时计算所需参数以及计算区域的选取。状态栏增加了计算云图信息,可在实时测量时调节云图的显示效果。

实时三维数字图像相关方法可在测量过程中实时显示被测区域变形、应变情况^[3],借此特点应用于教学实践中来培养学生定性分析问题的能力。测量的操作流程如下。

(1)准备教学试样

实验需准备：铝合金试样、三点弯梁模型、水转印散斑、加载装置、三脚架一套、两部相机、一台电脑。

试样尺寸测量：使用游标卡尺测量试样的几何形状尺寸。

(2)粘贴水转印^[10]散斑并安装试样

将水转印贴纸表面薄膜揭下后粘贴于待测试样表面,再将水转印贴纸浸湿并进行按压使散斑附着于待测试件表面,最后将水转印贴纸揭下即完成图9所示散斑布置。散斑布置完成后将试样安装到加载装置上,试样安装完成。

(3)架设相机并调节相机参数

相机架设：将三脚架架设在被测物体前,调整三脚架与待测物距离和高度。调节相机间距与夹角使待测区域位于相机画面中央。

相机参数调节：调节相机光圈至最大进光量后再调节曝光时间防止相机过曝,调节聚焦环至成像清晰。最后,调节光圈至5.6左右,再修改曝光时间至成像质量最佳。

(4)相机标定

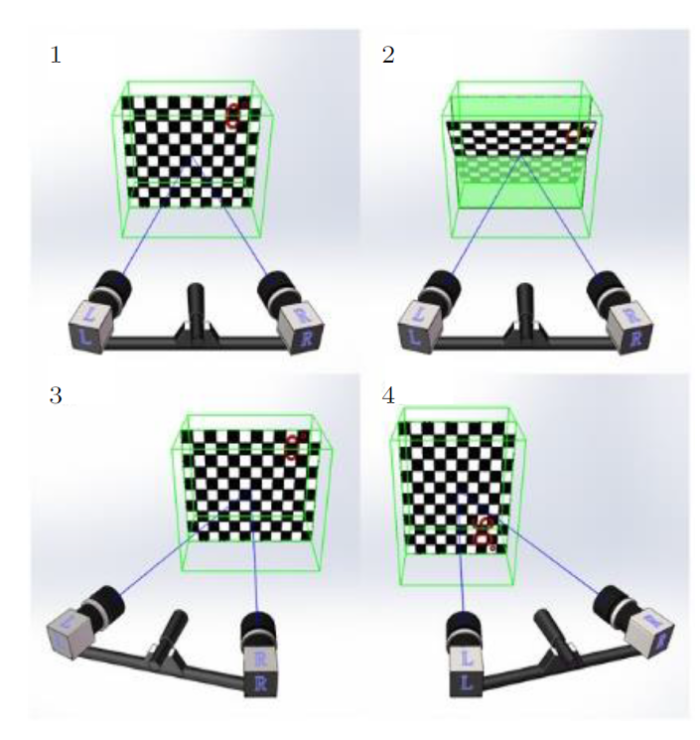
将标定板置于待测物前且尽量靠近待测物,保证标定板上所有内角点均在两部相机画面内,变换标定板姿态用软件采集若干次。姿态改变包括标定板的平移、旋转、倾斜等变换,避免待求参数发生耦合,如图10所示。

(5)设置计算参数后进行加载和实时计算

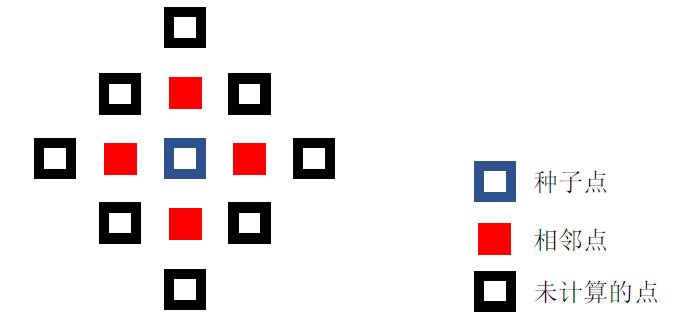
数字图像相关方法计算中需在软件中进行设置的计算参数有：计算区域、种子点、计算模板、计算步长和应变计算窗口大小。参数设置后可实时查看加载过程中的全场位移和应变信息。

(6)结合变形场数据学习材料力学基本方程

试样表面的变形可以实时显示出来,学生根据变形场即可对应分析其变形规律,并最终与材料力学书本上的变形基本方程进行对比分析。

(7)实验报告撰写

根据实验目标、实验结果以及实验分析撰写最后的实验报告。

实时三维数字图像相关测量软件具有实时显示、存储、处理数据的功能,能够实时展示实验加载中各项参数的变化效果,对于5000计算点,可以实现10 Hz以上的实时变形测量。

图11的铝合金拉伸实验数据显示,应变片与实时3D-DIC测量效果基本一致,在弹性阶段两种方法测量数据基本吻合。应变的测量结果可通过式(3)和式(4)进行验证

式中,$\Delta l$为选取的标距伸长量,$F_{\rm N}$为拉力大小,$l$为选取的标距长度,$E$为试样弹性模量,$A$为试样截面面积,$\varepsilon$为应变大小,$\sigma$为应力大小。

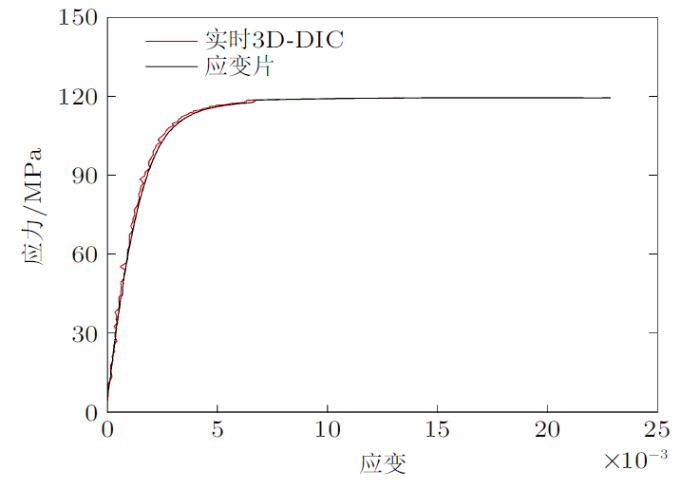
图12对比了两种方法的测量效果,两种方法均准确测得了弹性阶段的应力$\!-\!$应变曲线。结果显示：试样在应力达到100 MPa左右开始进入屈服阶段,两种测量方式的测量数据具有一致性。双相机测量有效消除了单相机测量时的离面位移误差影响,既达成了教学要求也提高了测量精度。

梁在加载过程中,图13通过实时的方式完整地展现了梁模型三点弯试样在受载时视场范围内的变形情况。在加载过程中可以实时查看计算区域内的变形和应变情况,界面右侧标尺上实时显示计算时不同颜色对应的数值范围。测量视场为200 mm时,系统位移测量误差的最大值小于0.01 mm,实时处理过程没有卡顿和延迟。既满足了实验要求,也达到了实验教学的效果。设$w$为梁上测点的挠度,$F$为载荷大小,$x$为测点到端点的距离,$I$为惯性矩,$l$为梁的长度, 三点弯梁的挠度测量结果可通过挠曲线方程进行验证

实时的可视化信息加深了学生对理论知识的理解,在调动了学习积极性的同时,培养了学生的逻辑分析能力,为后续教学工作的推进提供了良好的反馈。

同时,图形化实时观测具有形象直观的特点,对理解课程中梁应变分布以及圣维南原理等具有辅助作用。如图14所示,三点弯测试中,靠近中间集中载荷区域的竖直横截面上,剪应变$E_{xy}$分布会出现两个波包形式,这是与材料力学不一致的情况(根据材料力学分析应该是出现一个抛物线分布)。

本文运用实时三维数字图像相关方法对铝合金拉伸实验和梁模型的三点弯实验进行了教学展示,证实了实时三维数字图像相关方法应用在需要分析变形与受力的教学工作中具有效果直观、耗时短、操作简便等优点。

(1) 效果直观：实时三维数字图像相关方法直观地展示了实验过程中被测物的形变情况,在教学过程中可以根据变形实时地分析梁的受力状况,培养了学生进行受力分析的能力;

(2) 耗时短：在实验教学环节的工作中,与传统测量方法相比,省去了粘贴应变片和数据分析环节,缩短了实验周期;

(3) 操作简便：实验装置易操作,设备架设方便,上手快,散斑粘贴、相机标定、计算参数设定等均易操作。

未来,将根据实际需要设计更多的教学试样,开发开放式的教学软件,并配套教学讲义,将光测力学方法更多地用于实验教学^[11]中。