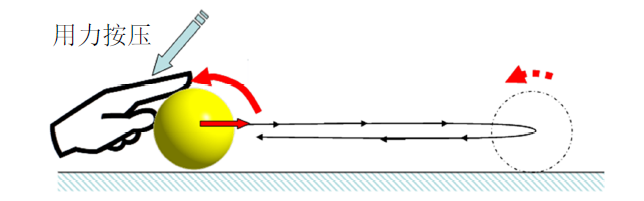
可能很多人尝试过用手指按压乒乓球,在一定条件下可以使它向前运动,然后又会返回(图1 )。本文从理论分析和数值计算的角度,对这一现象进行分析。
图1
乒乓球滚动问题的特点是,乒乓球可能打滑也可能不打滑,摩擦力或滚动摩阻的方向也可能发生变化,因此需要在不同阶段列写不同的方程再进行处理。
如果同时考虑空气阻力或滚动摩阻,不能获得所有的解析解,这也是本系列文章的一个目的:绝大部分动力学问题没有解析解,但是可以利用数值计算的方法获得系统所有参数变化的规律,加深对问题的理解。
1 乒乓球滚动的动力学方程及部分解析解
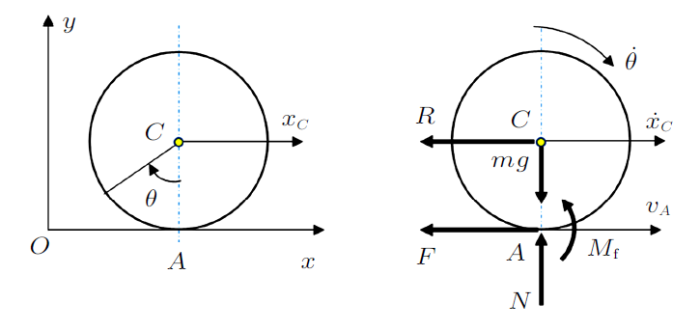
假设乒乓球质量为$m$,半径为$r$,水平面摩擦系数为$\mu $,滚动摩阻为$\delta$,空气阻力系数为$n$。乒乓球的运动和受力如图2 所示,其中$x_{C}$为乒乓球质心的运动,$\theta $为乒乓球的转角,$N$为压力,$F$为摩擦力,$M_{\rm f}=\delta N$为滚动摩阻,$R=n\dot{{x}}_{C} $为空气阻力。
图2
根据实际经验,乒乓球在初始阶段会打滑,后来会进入纯滚动状态,因此下面分两阶段来处理。第一阶段,乒乓球打滑前进(图2 ),可以列出动力学方程及补充的摩擦关系,为
(1) $\left. \begin{array}{l} m\ddot{{x}}_{C} =-F-n\dot{{x}}_{C} \\ 0=N-mg \\ J_{C} \ddot{{\theta }}=-\delta N+Fr \\ F=\mu N \\ \end{array} \right\}$
其中$J_{C} =2mr^{2}/3$是薄壁圆球对质心的转动惯量。令$\beta=n/(2m)$,方程(1)中的未知力消去后可以得到系统的运动微分方程,为
(2) $\left.\begin{array}{l} \ddot{{x}}_{C} +2\beta \dot{{x}}+\mu g=0 \\ \ddot{{\theta }}-\dfrac32(\mu r-\delta )g/r^{2}=0 \\ \end{array} \right\}$
方程(2)存在解析解,注意Matlab除了可以数值计算,还可以进行符号推导,包括对微分方程的积分[1 ] 。利用Matlab对方程(2)进行积分,源代码见图3 。
图3
图3 中syms为定义符号;diff(xc,t,2)表示xc对时间的2阶导数;dsolve表示对微分方程进行符号积分。运行后屏幕上显示方程(2)的解为
xc=C1+C2*exp(-2*beta*t) - (g*mu*t)/(2*beta)
theta=C4+C3*t-(t^ 2*(3*delta*g-3*g*mu*r))/(4*r^ 2)
(3) $\left.\begin{array}{l} x_{C} =\dfrac14\left( {g\mu /\beta^{2}-2\dot{{x}}_{0} /\beta} \right)(1-{\rm e}^{-2\beta t})-\\[3mm]\qquad \dfrac12g\mu t/\beta \\[3mm] \theta =\dfrac34(\mu r-\delta )gt^{2}/r^{2}+\dot{{\theta}}_{0} t \\ \end{array} \right\}$
这一阶段结束的标志是接触点$A$速度为零。$A$点速度根据图2 可以分解为牵连速度$v_{\rm e}=\dot{{x}}_{C} $和相对速度$v_{\rm r} =r\dot{{\theta }}$,代入式(3)处理后有
(4) $\left( {\dot{{x}}_{0} -\frac12g\mu / \beta } \right){ e}^{-2 \beta}-\frac32(\mu r-\delta )gt/r-\ \ \frac12g\mu / \beta-r\dot{{\theta }}_{0} =0$
设$t^{\ast}$时刻触点$A$速度为零,在退化情况下方程(4)可以有解析解,但是在一般情况下没有$t^{\ast}$的解析表达式(这将导致后续分析出现问题)。不过在数值积分中$t^{\ast}$可以利用积分中断获得,这表明了在一般情况下利用数值计算的潜力。
第二阶段,乒乓球作纯滚动,但乒乓球可能向前运动也可能向后运动,滚动摩阻的方向相应也应改变,定义方向函数
(5) $\lambda =\left\{ {\begin{array}{ll} +1,& {\rm if}\mbox{ }v_{C} >0 \\ 0, & {\rm if}\mbox{ }v_{C} =0 \\ -1,& {\rm if}\mbox{ }v_{C} <0 \\ \end{array}} \right.$
注意这一阶段$A$点速度为零,此时动力学方程及补充运动学关系为
(6) $\left.\begin{array}{l} m\ddot{{x}}_{C} =-F-n\dot{{x}}_{C} \\ 0=N-mg \\ J_{C} \ddot{{\theta }}=-\lambda \delta N+Fr \\ \ddot{{x}}_{C} =r\ddot{{\theta }} \\ \end{array} \right\}$
(7) $\ddot{{x}}_{C} +\frac65\beta \dot{{x}}_{C} +\frac35g\lambda \delta /r=0$
(8) $x_{C} =C_{1} +C_{2} {\rm e}^{-6\beta t/5}-\lambda gt/(2\beta r)$
问题在于,由于第一阶段结束的时间$t^{\ast }$以及$x_{C} (t^{\ast})$和$\dot{{x}}_{C} (t^{\ast})$没有解析表达式,方程(8)中的积分常数无法确定,因此无法得到更多的理论解。
由于在一般情况下很难得到动力学问题的全部解析解,下面介绍数值计算。
2 微分方程的分段准备工作
首先把第一、二阶段的动力学方程(1)和(6)转换为$ A X= B$的形式,分别为
(9) $\left[ {{\begin{array}{c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c} m & 0 & 1 & 0 \\ 0 & {J_{C} } & {-r} & \delta \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & {-\mu } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\ddot{{x}}_{C} } \\ {\ddot{{\theta }}} \\ F \\ N \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} {-n\dot{{x}}} \\ 0 \\ {mg} \\ 0 \\ \end{array} }} \right]$
(10) $\left[ {{\begin{array}{c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c} m & 0 & 1 & 0 \\ 0 & {J_{C} } & {-r} & {\lambda \delta } \\ 0 & 0 & 0 & 1 \\ 1 & {-r} & 0 & 0 \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\ddot{{x}}_{C} } \\ {\ddot{{\theta }}} \\ F \\ N \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} {-n\dot{{x}}} \\ 0 \\ {mg} \\ 0 \\ \end{array} }} \right]$
这是混合形式的微分代数方程。在数值计算中,当前$t$时刻的$x_{C},\theta,\dot{{x}}_{C},\dot{{\theta }}$是已知量,而$\ddot{{x}}_{C},\ddot{{\theta}},F,N$是未知量,因此先把$\ddot{{x}}_{C}$和$\ddot{{\theta }}$视为代数量,调用$X=$inv($A)$*$B$求出当前时刻的$\ddot{{x}}^{\ast}_{C}$和$\ddot{{\theta }}^{\ast}$(求解后已经是具体数值),再把动力学方程转换为标准的一阶方程组形式,设
(11) $y_{1} =x_{C},\ \ y_{2} =\dot{{x}}_{C},\ \ y_{3} =\theta,\ \ y_{4} =\dot{{\theta }}$
(12) $\left. {\begin{array}{l} \dot{{y}}_{1} =y_{2} \\ \dot{{y}}_{2} =\ddot{{x}}_{C}^{\ast } \\ \dot{{y}}_{3} =y_{4} \\ \dot{{y}}_{4} =\ddot{{\theta }}^{\ast } \\ \end{array}} \right.,\ \ \left. {\begin{array}{l} y_{1} (0)=0 \\ y_{2} (0)=\dot{{x}}_{C} (0) \\ y_{3} (0)=0 \\ y_{4} (0)=\dot{{\theta }}(0) \\ \end{array}} \right\}$
第一阶段和第二阶段的分界点时刻$t^{\ast}$可以由Matlab积分时的中断条件获得。在积分之前,先把积分中具体的要求在options中说明,其格式为
(13) $\text{options }=\text{odeset} (\text{$'$RelTol$'$,} number1, \text{$'$AbsTol$'$},\ \ number2, \text{$'$events$'$},@event_ name);$
格式中黑正体表示固定格式,白斜体表示变量。注意 'events',@ 表示在积分时会调用名为$event_name$这个子程序,具体的中断条件可以在该子程序中表达,在本问题中即$A$点速度为零。在设定积分条件后,再调用积分函数,其格式为
(14) $[t,y]=\text{ ode45(@}rg_ kt_ name,[start_ time:\ \ step_ time: end_ time], y0, \text{ options);}$
格式中黑正体表示固定格式,白斜体表示变量。其中$[t,y]$是积分的时间和结果;动力学方程在子程序$rg_ kt_ name$中描述;$y$是初始条件;如果没有中断条件,积分时按等步长$step_ time$从$start_ time$开始到$end_time$结束,有中断条件后,最后一步的积分步长会自动调整,结束时间也会自动提前。
在程序中先给参数赋值,然后分段计算,这一部分的源代码见图4 。
图4
图4 中rg_ kt_ pingpang1,rg_kt_pingpang2分别根据方程(9)和方程(10)解出的结果进行积分;在event_pingpang1中满足$A$点速度为零就中断积分;第一阶段结束后把最后时刻的参数赋给tf和new_y0作为第二阶段的初值,再进行第二阶段积分。第一阶段具体中断的条件见图5 。
图5
3 数值计算与解析解的比较
在正式进行大量计算前,首先对程序进行一些测试。由于第一阶段有解析解,可以用于验证数值积分。下面参数在所有计算中保持不变
$m=3~{\rm g},\ \ r=2~{\rm cm},\ \ g=9.8~{\rm m/s}^{2}\ \ \mu =0.3,\ \ J_{C} =\frac23mr^{2},\ \ x_{C} (0)=0\ \ \dot{{x}}_{C}(0)=1~{\rm m/s},\ \ \theta (0)=0$
而$\dot{{\theta }}_{0}$, $\beta =n/(2m)$, $\delta $根据情况改变。
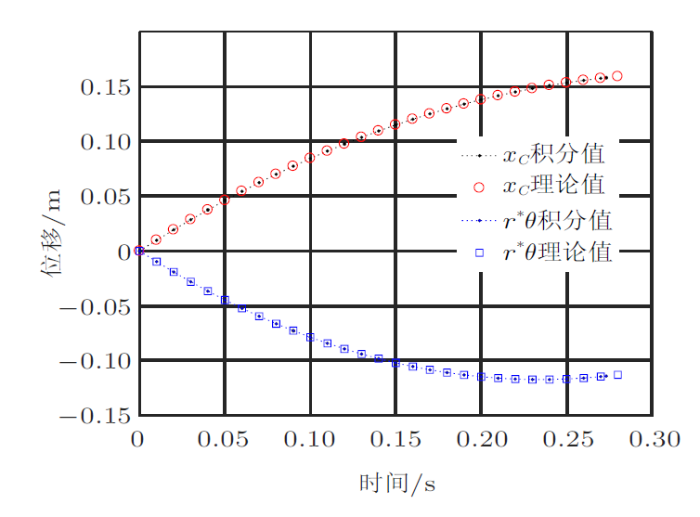
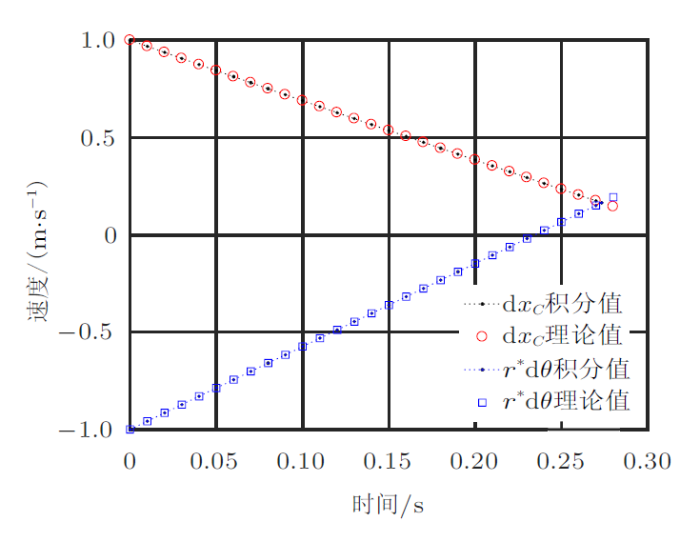
取$\dot{{\theta }}_{0} =-50$ rad/s, $\beta =0.1$, $\delta =r/100$,第一阶段的位移和速度曲线见图6 和图7 。数值解(圆点)与解析解(位移用圆圈,半径与角度乘积用方框)对比表明,两者很吻合,只有最后一个圆圈或方框与圆点不重合。原因是数值计算中运用了中断,最后一步不是等步长的;而解析解的最后一步的时间没有解析表达式,按等步长来处理。
图6
图7
图6 和图7 的结果表明数值计算的精度很好(在前面文章中已介绍精度$\sim10^{-10}$),另一方面,把解析解与数值解结合起来,可以取长补短,更好地处理第二阶段的情况。
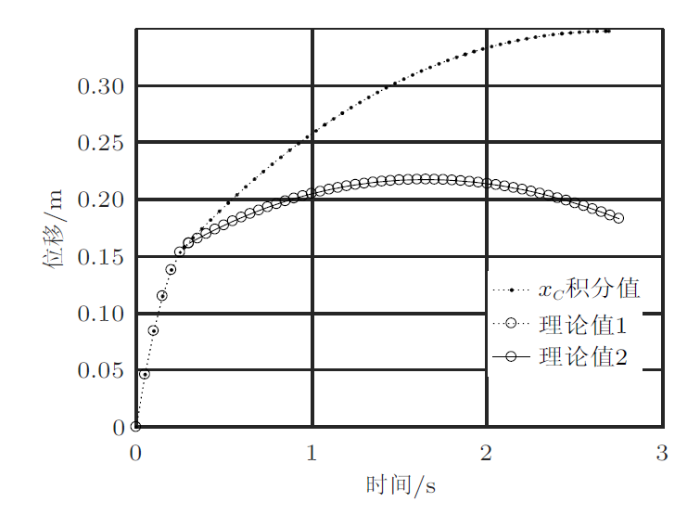
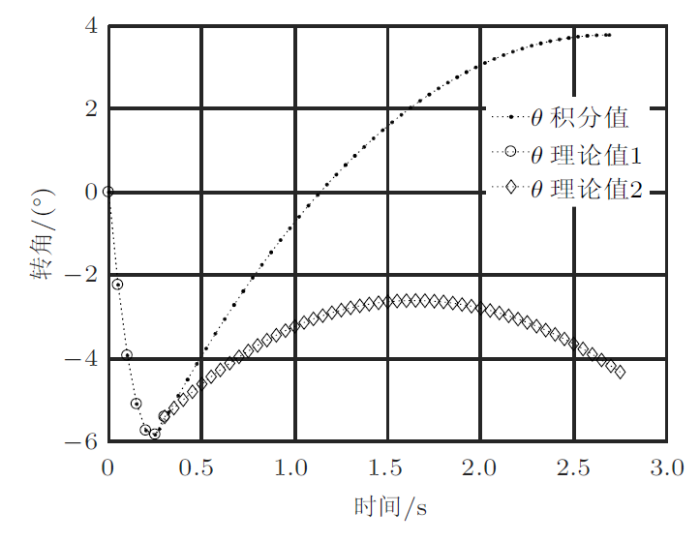
第二阶段也有解析解,但把数值计算与解析解进行对比,发现第一阶段数值解与理论解吻合,第二阶段差别很大(图8 和图9 )。原因是方程(8)中的参数与第一阶段的中止时间有关,由于没有解析解,于是按等步长来计算时间,导致解出的常数$C_{1}$和$C_{2}$有偏差(表1 给出了第一阶段终止时刻的理论解和数值解)。
图8
图9
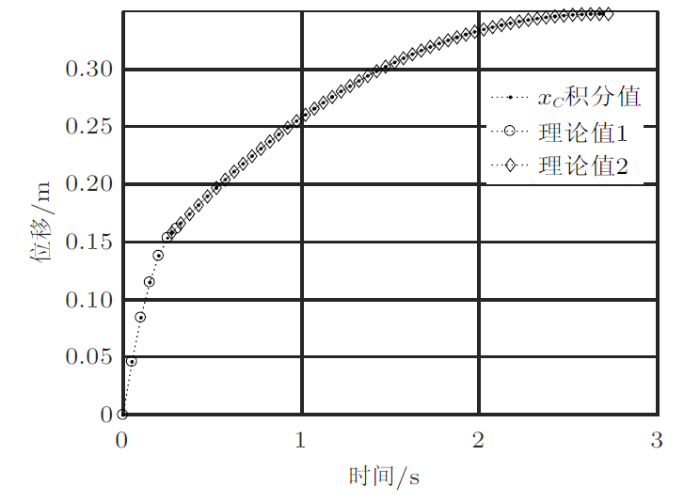
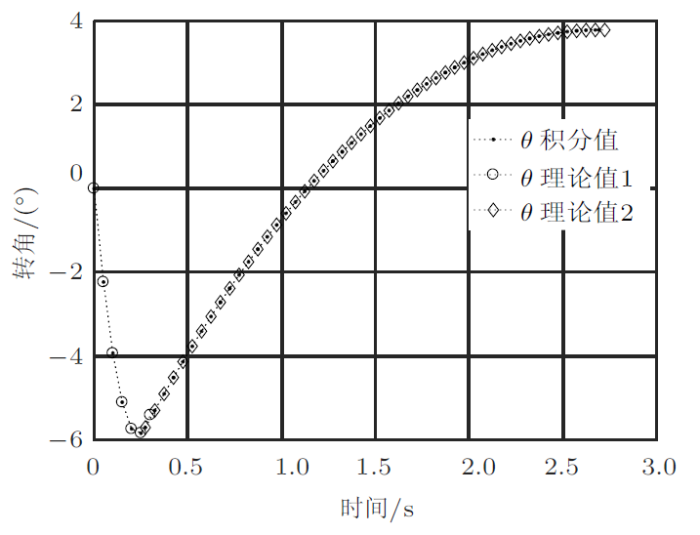
如果用第一阶段数值计算中断时的最后结果来确定第二阶段的解析解中的初始条件,可以发现两阶段的数值解(圆点)全部落在代表解析解的圆圈或菱形中了(图10 和图11 )。这一结论既证明了数值解的精确性,也表明了解析解与数值解结合的潜力。
图10
图11
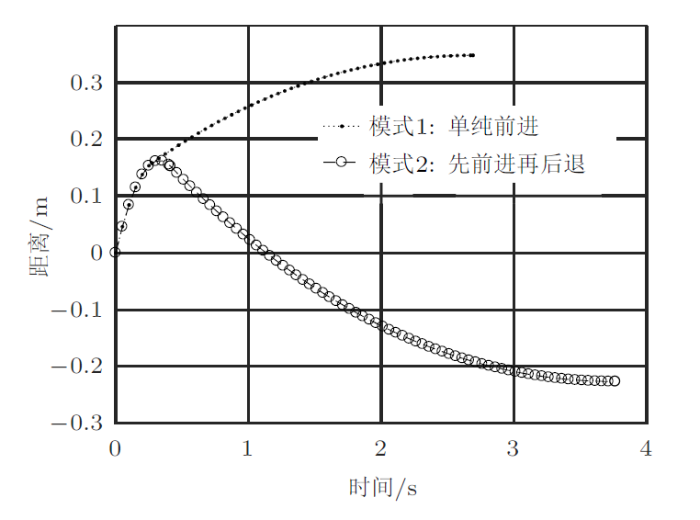
有了前面的验证,计算的可靠性有了保证。 乒乓球游戏有两种结果:模式1初始角速度小,乒乓球只会前进不能后退;模式2初始角速度大,乒乓球先前进再后退。
(15) $\left.\begin{array}{l} \dot{{x}}_{C} =\dfrac12\left( {g\mu / \beta -2\dot{{x}}_{0} } \right){\rm e}^{-2\beta t}-\dfrac12g\mu /\beta \\[1.5mm] \dot{{\theta }}=\dfrac32(\mu r-\delta )gt/r^{2}+\dot{{\theta}}_{0} \\ \end{array} \right\}$
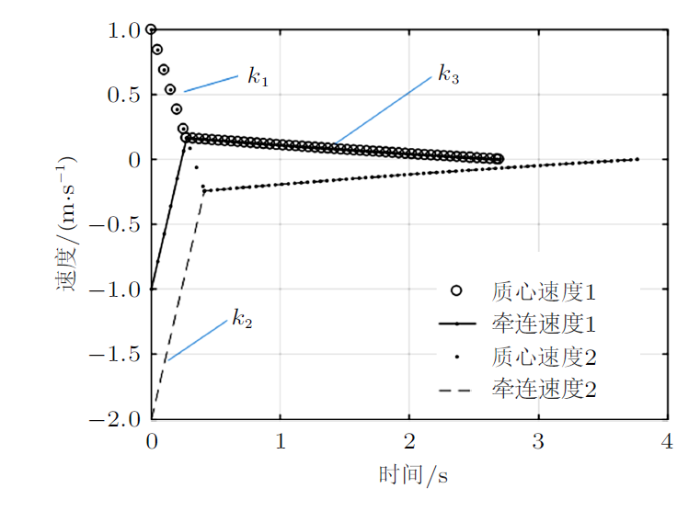
在第一阶段,质心速度在小阻尼时,利用${\rm e}^{-2\beta t}\approx 1-2\beta t$,其斜率$k_{1} \approx 2\beta \dot{{x}}_{0} -g\mu$;牵连速度$r\dot{{\theta }}$的斜率是$k_{2} =(3/2)(\mu-\delta /r)g$,在第二阶段,质心速度的斜率$k_{3} =(3/5)g\lambda \delta /r$。
但是当$A$点速度为0时(牵连速度与相对速度曲线相交),乒乓球就开始作纯滚动,模式1中乒乓球继续前进,模式2中乒乓球会返回(图12 );而在速度图中,牵连速度与相对速度会一直相等且逐渐变为0 (静止状态),模式1速度从正趋于0 (一直前进),模式2速度从负趋于0 (先前进再后退),见图13 。
图12
图13
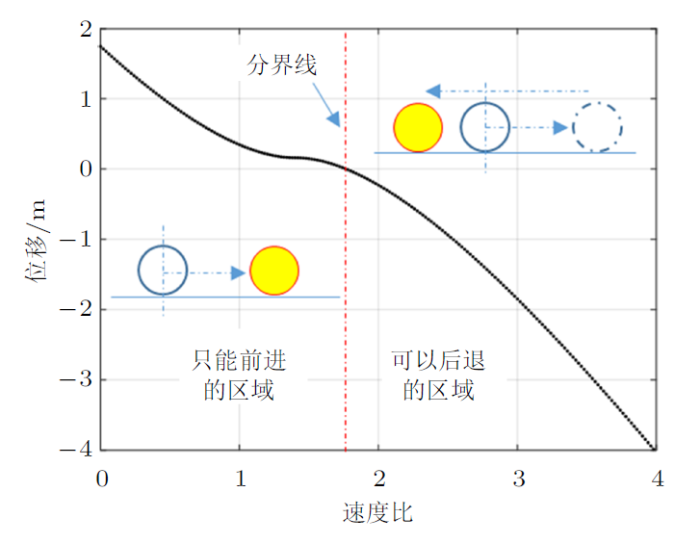
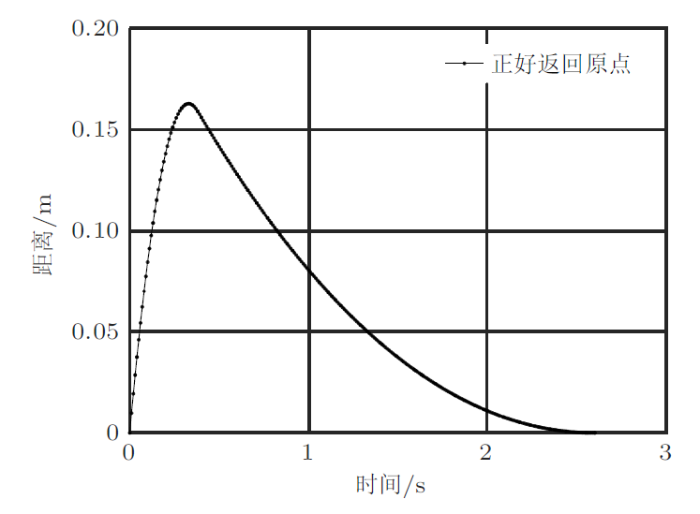
如果关心角速度对最终位移的影响,可以把初始速度比(定义为$|{r\dot{{\theta }}_{0} /\dot{{x}}_{C0}}|$,即牵连速度与质心速度之比)作为横坐标,进行大量计算得出曲线如 图14 所示,存在一条分界线,分界线左侧(角速度较小)乒乓球最终停在前方(包括先前进再后退,但停在出发点前方),分界线右侧(角速度较大)乒乓球最终会停在出发点的后方。如果希望乒乓球向前运动后返回,正好返回原点,初始角速度是多少(注意方程(8)没有解析解)?Matlab可以把图形放大,只需要把图14 中分界线与曲线的交点区域不断放大,就能得到分界线处的速度比值是1.770 665 387 040 5,然后以这样的速度比值单独再算一次,就可以让乒乓球先前进然后正好退回到原点(图15 )。
图14
图15
4 小结
本文讨论了乒乓球运动的理论解和数值解。在退化情况下,可以获得全部解析解,而在一般情况下(如同时考虑摩擦、滚动摩阻、空气阻力),只能得到很少的解析解,而采用数值计算的方法可获得一般情况下所关心的所有参数。
(1)乒乓球的运动分不同的阶段,本文介绍了在Matlab (R2016b版本)中如何处理分段计算的方法,以及微分代数方程求解的一般过程。
(3)适当运用Matlab中的符号推导,可以获得部分解析解表达式(包括部分微分方程的解析解)。
(4)通过计算,得到了一般情况下乒乓球运动的规律,例如在初始速度一定时,找到了初始角速度和质心最终位移的关系,得到了乒乓球质心最终是否前进的分界线的解,也可以让乒乓球正好返回原处。这些结论在一般情况下都没有解析解。
参考文献
View Option
[1]
甘勤涛 , 胡仁喜 , 程政田 等 . Matlab数学计算与工程分析从入门到精通 . 北京 : 机械工业出版社 , 2019
[本文引用: 1]
1
2019
... 方程(2)存在解析解,注意Matlab除了可以数值计算,还可以进行符号推导,包括对微分方程的积分[1 ] .利用Matlab对方程(2)进行积分,源代码见图3 . ...