作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] 。导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] 。王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法。文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变。然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异。文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性。综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关。目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究。为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响。
1 新型输电导线内嵌式接续管与传统接续管对比结构的特点
新型输电导线内嵌式接续管由外层铝接续管、外嵌层变台阶铝管和内嵌层管构成。外层铝接续管提供圆线同心绞架空导线对接主要的抗张力和接头压力,内外嵌层铝管分别提供压接部分钢丝、铝丝嵌入填充材料,利用铝合金的高静摩擦系数将接头压力转变为抗张力,提高接头的握着力。
相比于传统的接续管,新型输电导线内嵌式接续管内外嵌层铝管硬度低,不会压伤19绞架空同心钢芯铝绞线,只要模具跟压接管匹配,压接头不会出现欠压、松股现象,因此可以不用对压接头进行无损检测。
传统接续管具有如下问题:(1) 导线接续处各部分结构线膨胀系数不同,导致温度变化时接续处出现裂缝;(2)现有钢芯铝绞线接续管在使用过程中,由于材料及压接工艺存在不足,常造成钢芯压伤疲劳断股;(3)压接后铝绞线、铝合金接续管出现屈服硬化,热膨胀不一致无法补偿,接续管与铝绞线压接部位产生缝隙,空气和水进入后氧化,接续管与铝绞线压接部位接触电阻增大发热,导线接续失效断线。相较于传统接续管,新型接续管具有接续管结构温升低于导线温升、整体结构压接后握力不小于高压输电导线额定拉断力的95%、插层铝管材料电导无限接近铝绞线且弹性模量在钢铝之间等特点。此外,新型接续管对各部分结构进行了防腐处理,结构内部能够起到防腐蚀作用,并且母铝管内壁特殊处理,弥补了插层设置导致的结构特殊性。
2 内嵌式钢芯铝绞线接续管振动疲劳响应数学模型
2.1 建立钢芯铝绞线接续管振动疲劳响应数学模型
钢芯铝绞线接续管的疲劳损伤在风振作用下可分为两个阶段,第一阶段为损伤阶段,此阶段结构未出现宏观裂纹,采用塑性流动法进行计算;第二阶段为断裂阶段,此时接续管出现宏观裂纹,此阶段应用强度因子理论进行计算。可通过对两个阶段的描述来定义钢芯铝绞线接续管的疲劳寿命。
2.2 塑性流动法求解接续管损伤阶段疲劳响应数学模型
局部反复塑性形变会导致接续管疲劳损伤,因此管辖瞬时塑性流动的损伤发展方程为
(1) $D=\frac{\sigma^{b-1}{\dot{\sigma}_{\rm r} }}{B(1-D)^{b}}$
式中,$B$和$b$分别为与钢芯铝绞线结构有关的参数,$\sigma $为钢芯铝绞线接续管的使用应力,$\sigma_{\rm r}$为钢芯铝绞线接续管在风振作用下的动弯应力,$D$为损伤变量。
对式(1)积分一个反复载荷周期便可得出每个周期的损伤量d$D$/d$N$ ($N$为损伤循环次数)。经过一个反复载荷周期积分,钢芯铝绞线接续管在风振作用下的动弯应力$\sigma_{\rm r} $只与载荷循环中的最大应力$\sigma_{\max}$和最
小应力$\sigma_{\min}$有关,假定在一个周期中的损伤变化下,积分过程中$D$视为常数,可得
(2) $\frac{{\rm d}D}{{\rm d}N}=2\int_{\sigma_{\min } }^{\sigma_{\max}}{{\rm d}D} =\frac{2(\sigma_{\max}^{b} -\sigma_{\min }^{b} )}{bB(1-D)^{b}}$
当$D=1$时结束此阶段计算,此时材料出现裂纹。当$N$到达破坏载荷循环周数$N_{\rm I}$时,
(3) $N_{{\rm I}} =\frac{bB}{2(b+1)(\sigma_{\max}^{b}-\sigma_{\min }^{b} )}$
(4) $D=1-\lt(1-\frac{N}{N_{{\rm I}} })^{1/(b+1)}$
考虑到钢芯铝绞线振动下的应力幅值以及钢芯铝绞线接续管压接后材料的结构参数,为了表示钢芯铝绞线接续管的动弯疲劳应力$\sigma_{a}$与导线架设张力状态下的应力$\sigma_{u}$之比,引入了$S_{a}=\sigma_{a}/\sigma_{u}$,即
(5) $\frac{{\rm d}D}{{\rm d}N}=[1-(1-D)^{\beta +1}]^{\alpha (S_{M},S_{0})}\lt[\frac{S_{a} }{M(S_{0} )(1-D)}]^{\beta}$
式中,$\alpha$和$\beta $为与压接管的压接尺寸及钢芯铝绞线型号有关的参数,可由相关钢芯铝绞线$S$-$N$曲线得出;$M$ ($S_{0}$)为与钢芯铝绞线接续管微风振动相关的参数,可由具体工况取得;$S_M$为输电线风振疲劳应力与导线架设张力状态下的应力;$S_0$为接续管产生初始裂纹时疲劳应力与导线架设张力状态下的应力。
2.3 强度因子法求解接续管断裂阶段疲劳寿命数学模型
假设钢芯铝绞线接续管的管壁厚度为$h$,平均的曲率半径为$r$,裂纹长度为$a$,损伤后初始的裂纹长度为$a_{0}$,接续管裂纹长度为$a$时接续管的拉伸张力为$F_{\rm s}$,风速大小为$v$,裂纹长度折算系数为$\lambda$,接续管所在位置承受的动弯张力为$N_{0}$、应力为$\sigma_{\rm r}$,其拉伸强度因子为
(6) $K_{\rm I} =F_{\rm s} (\lambda a_{0} )\sigma_{\rm r} \sqrt {\pi a}$
利用Origin选取数据,作散点图,然后选择线性拟合,对式(6)进行曲线拟合,得到曲线关系为
(7) $F_{\rm s} =0.124 82 \lambda a$
(8) $\lambda a=\left[12-\left(1-v^{2}\right)\right]^{{1}/{4}} a / \sqrt{r h}$
$\frac{{\rm d}a}{{\rm d}N}=f\left( {\sigma,a,c} \right)=f\left( {K,R}\right)$
其中$K$为应力强度因子,$R$为循环应力比,$c$为材料常数,得
(9) $\frac{{\rm d}a}{{\rm d}N}=c\left[K(1-R)^{s}\right]^i,$
令$\left[12-\left(1-v^{2}\right)\right]^{{1}/{4}}=\eta$,得
(10) $\frac{{\rm d}a}{{\rm d}N}=c\lt[\eta \sqrt {\pi rh\sigma_{\rm r} }a^{{3}/{2}}(1-R)^{s}]^{i}$
接续管裂纹从$a_{0}$扩展到$a_{c}$ ($a_{c}$为裂纹扩展到$c$位置时的裂纹长度)的疲劳寿命为$N_{\rm II}$,则对式(9)和式(10)两边进行积分得
(11) $\hspace{-4mm}\int_{a_{0}}^{a_{c}} a^{3n/2} =\ \\ \hspace{-4mm} \int_0^{N_{\rm II}} c\left[ {\eta\sqrt {\pi rh} \sigma_{\rm r} a^{3/2}(1-R)^{s}}\right]^{i}{\rm d}N_{\rm II}$
(12) $N_{\rm II} =\frac{2\lt(a_{c}^{1+3n/2} -a_{0}^{1+3n/2})}{c(2+3n)\left[ {\left[ {12(1-v^{2})}\right]^{{1}/{4}}(1-R)^{s}\sigma_{\rm r} \sqrt {\pi rh} } \right]^{i}}$
3 内嵌式钢芯铝绞线接续管振动疲劳响应特性仿真分析
以LGJ-240/30型号的钢芯铝绞线接续管为仿真模型,将塑性流动法和强度因子理论编写至COMSOL仿真软件,分析钢芯铝绞线接续管风振响应以及不同压接对边尺寸下的内嵌式钢芯铝绞线接续管疲劳响应特性。
3.1 建立内嵌式钢芯铝绞线接续管风振响应仿真模型
LGJ-240/30钢芯铝绞线接续管具体参数为:泊松比$\nu=0.33$,杨氏模量$E=1.46\times 10^{11}$ Pa,密度$\rho =5 000$ kg/m$^{3}$。
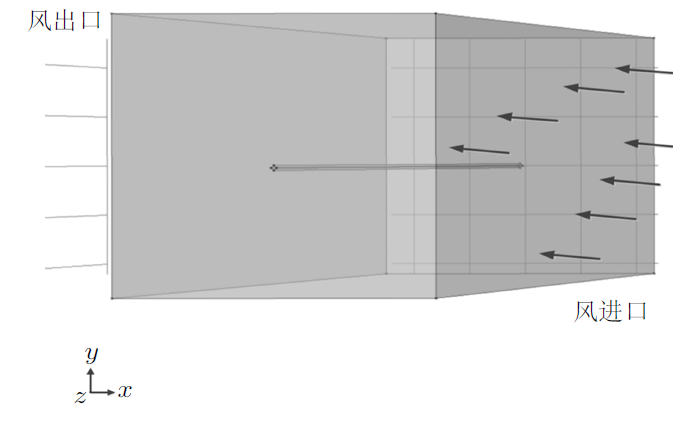
设置档距为100 m,档距内的接续管正好在整档1/4位置处压接,同时设置长为100 m,高和宽均为2.4 m的风域,建立有限元模型,如图1 。
图1
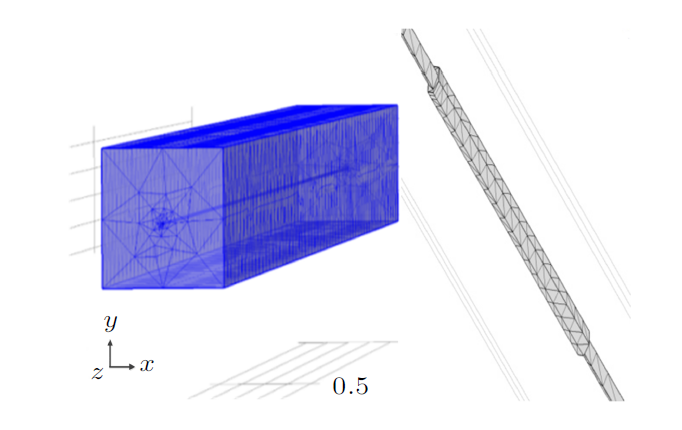
设定流场风速为5.08 m/s,频率为10 Hz,入口位置仅有法向速度,同时设置流场域上下壁为对称边界,以极细四面体网格作为网格划分的钢芯铝绞线,在档距内靠左端1/4位置处的接续管管口处设置接续管以设置边界层网格,网格划分如图2 。
图2
3.2 内嵌式钢芯铝绞线接续管风振响应分析
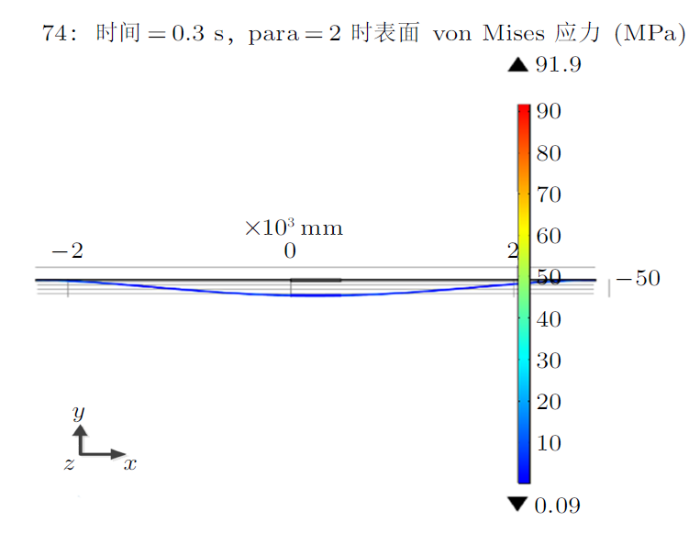
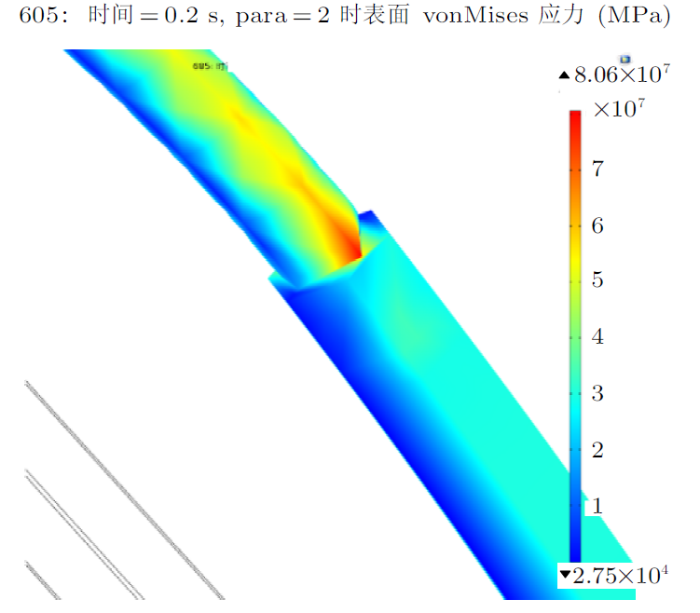
设定流场风速为5.08 m/s,频率为10 Hz,在一个波形循环内,接续管前后2.5 m处的应力分布如图3 ,管口绞线变形及应力如图4 。
图3
图4
由图3 和图4 可知, 在一个波形内,钢芯铝绞线接续管于0.3 s 与0.5 s 时应力最大,相较于管体及相邻绞线管口绞线处应力最大。
对不同额定拉断力工况下的接续管管体及管口绞线的应变进行分析和对比,各工况下接续管管体及管口绞线应变情况分别如图5 $\sim\!$图7 所示。
图5
图5
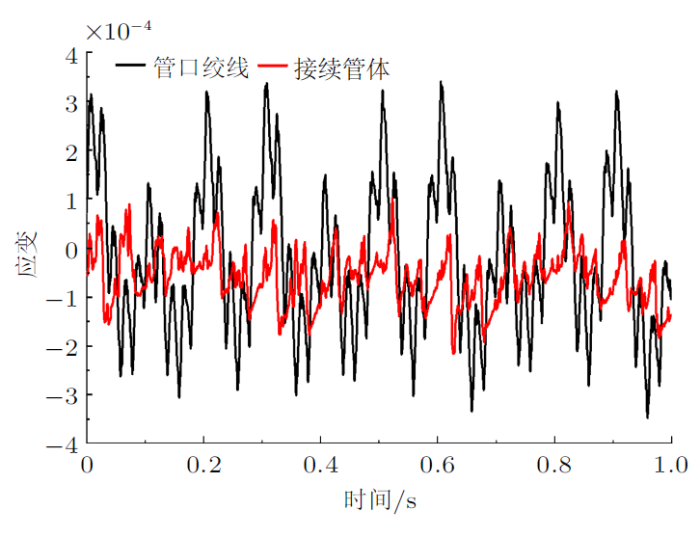
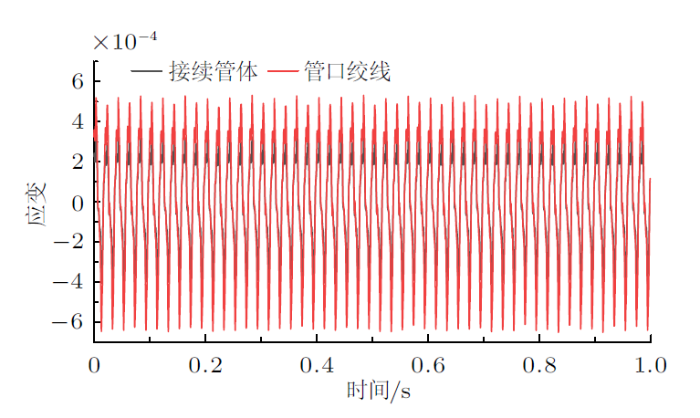
15%额定拉断力工况下接续管管体及管口绞线应变
图6
图6
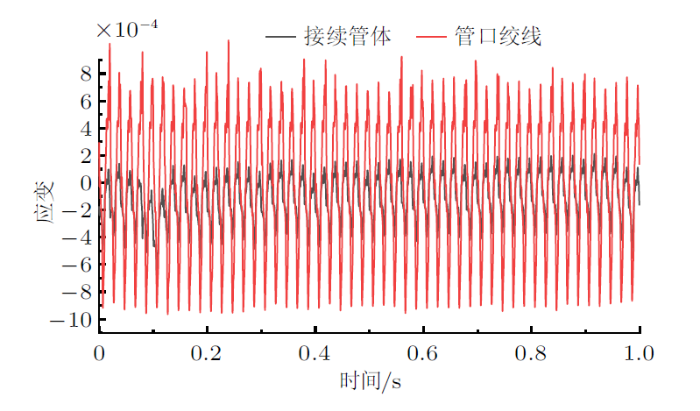
20%额定拉断力工况下接续管管体及管口绞线应变
图7
图7
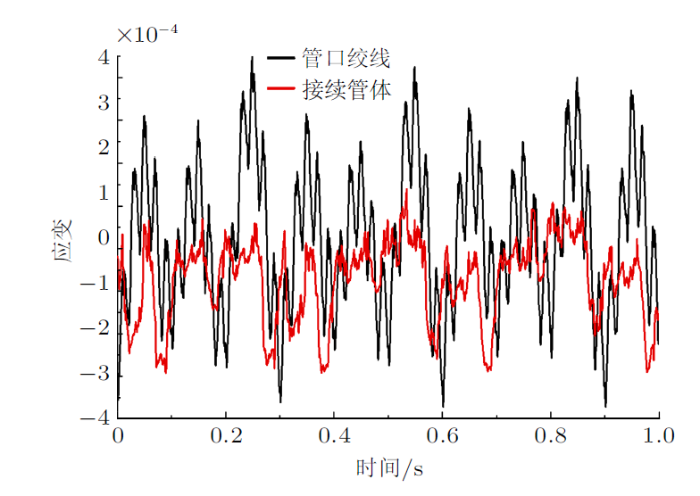
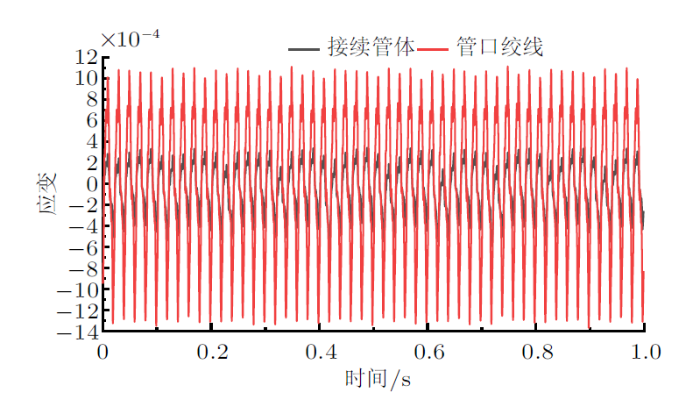
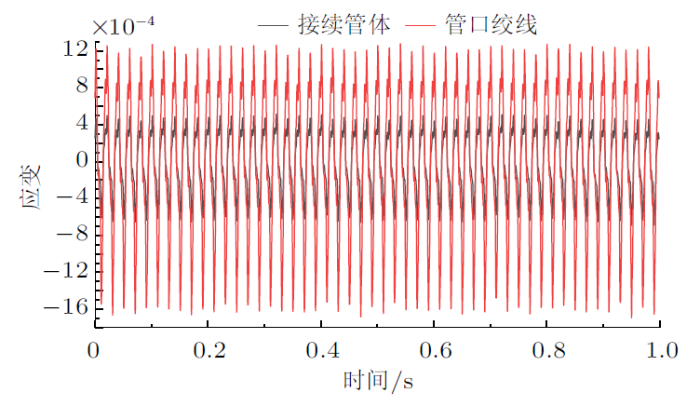
25%额定拉断力工况下接续管管体及管口绞线应变
由图5 $\sim\!$图7 可知,导线张力从15%额定拉断力增大到25%额定拉断力时,管口绞线应变有效值从$1.863\times10^{-4}$增大到$4.162\times10^{-4}$,且管体与其余段铝绞线要远远小于管口绞线的应力应变。
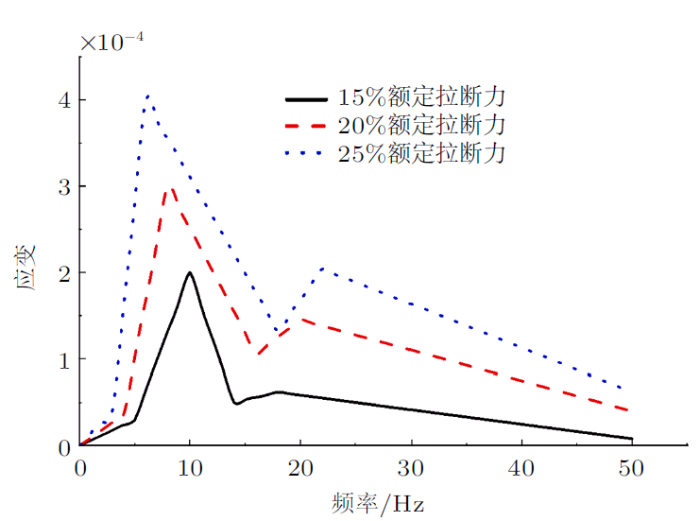
计算不同风频下管口绞线的动弯应变,得到差异张力下管口绞线的应变如图8 。
图8
由图8 可知,当张力设定为导线计算拉断力15%时,导线的动弯应变在10.32 Hz时产生峰值,为$1.926\times10^{-4}$。随着风频率的增大,动弯应变随之减小且在频率为14.6 Hz时出现谷值为$3.12\times10^{-5}$。当张力设定为导线计算拉断力20%时,导线的动弯应变在7.98 Hz时产生峰值,为$3.032 1\times10^{-4}$。当导线为25%额定拉断力情况下,动弯应变曲线出现的第1个峰值跳跃点的风频率将提前,第二个峰值点的风频率有增大趋势。
3.3 不同压接对边尺寸下的内嵌式钢芯铝绞线接续管疲劳响应
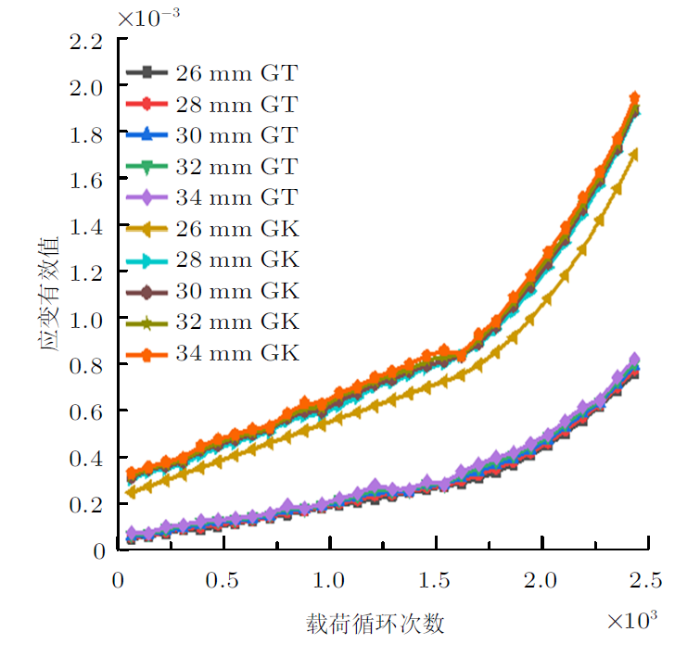
设定导线两端25%额定拉断力作为固体力学物理场,计算在不同压接对边尺寸工况下的疲劳特性响应,每振动100万次采集一次波形内管体及绞线动弯应变的最大值,计算结果如图9 ,其中,GK为接续管压接对边尺寸长边单位长度,GT为为接续管压接对边尺寸短边单位长度。
图9
由图9 可知,随着振动次数的增加,接续管及管口绞线整体的动弯应变呈现上升的趋势。接续管口绞线的应变为管体的2.6倍左右,随着压接对边尺寸的增大,接续管及管体绞线的动弯应变呈现下降趋势,且在对边尺寸为30 mm时动弯应变达到最小值,再增大尺寸时动弯应变也随之增大。
对压接对边尺寸为30 mm下的最后一模压接长度下的管体及管口绞线动弯应变情况进行计算,每计算100万次收集一次振动万次内的最大应变值,如图10 。
图10
由图10 可知,管口绞线动弯应变随着振动次数增加而呈现增大的趋势,从初始动弯应变为$2.215 8\times10^{-4}$增加到最终动弯应变为$9.026 8\times10^{-4}$,各种工况差距不大,随着最后一模压接长度的增大,管口绞线的疲劳源区愈加明显。
4 内嵌式钢芯铝绞线接续管风振疲劳试验
为进一步研究钢芯铝绞线接续管振动作用下接续管管体和管绞线的疲劳特性,采用与仿真相同的模型对25%额定拉断力工况下的钢芯铝绞线接续管疲劳振幅及应变进行分析,同时使用扫描电子显微镜(scanning electron microscope, SEM)扫描采集接续管及管口裂缝长度,并对接续管疲劳试验中的动弯应变进行采集,通过与仿真结果进行对比,发现数据基本吻合,从而验证了仿真计算结果的正确性。
4.1 试验对象及试验手段
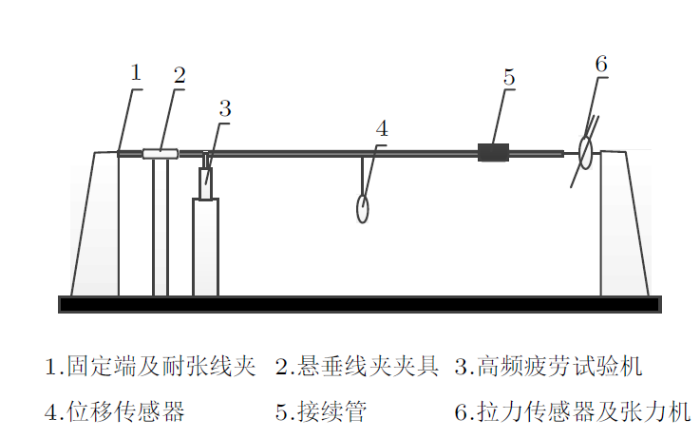
以LGJ-240/30钢芯铝绞线和YJD-240/30钢芯铝绞线接续管为试验对象,试验布置图及现场图分别如图11 和图12 ,现场压接图如图13 。
图11
图12
图13
通过对钢芯铝绞线的一端施加导线额定拉断力为25%的张力,并在接续管及管口绞线位置处粘贴应变片连接计算机以便收集数据,连接高频疲劳试验机并输入振动波,得到每百万次接续管管体及管口绞线应变数据。
4.2 25%额定拉断力下的内嵌式钢芯铝绞线接续管疲劳振幅分析
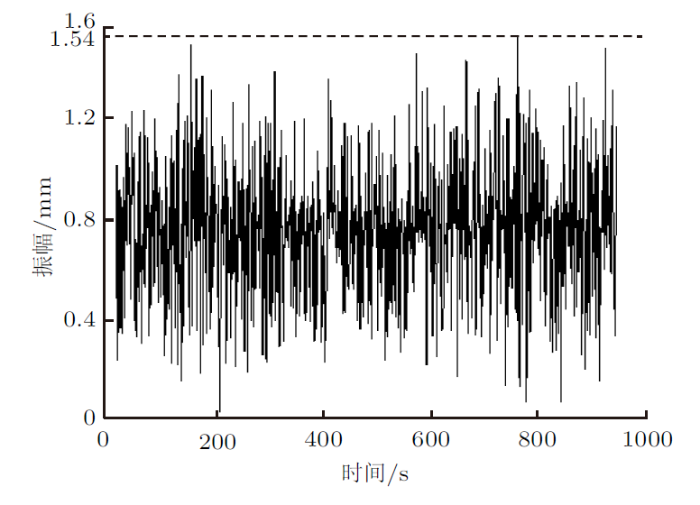
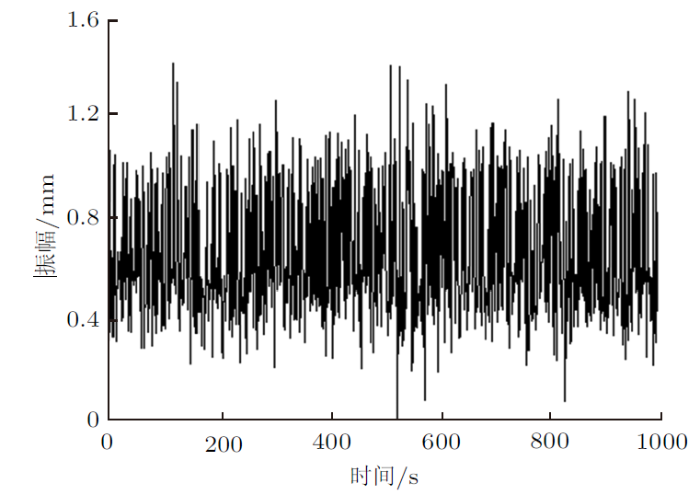
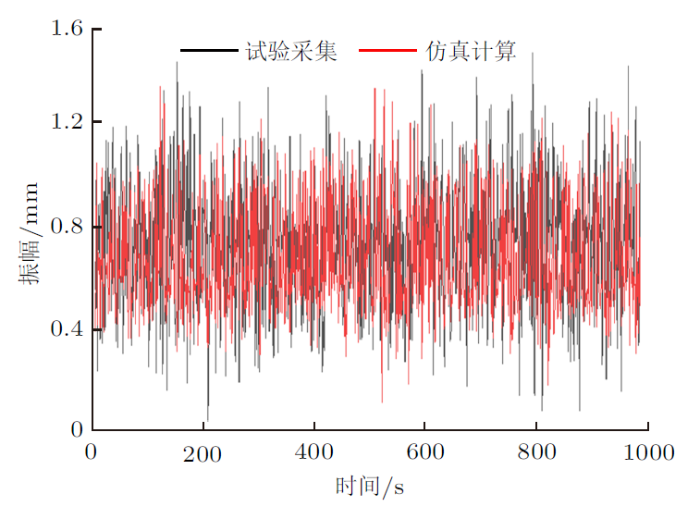
在采集钢芯铝绞线接续管处及线夹出口处在循环载荷下的振幅后,结果呈现为两处振幅最大值和振动轨迹相似,与计算仿真结果轨迹相似,振幅值大致相同。仿真计算振幅值、试验采集振幅值、仿真计算与试验采集振幅值对比分别如图14 $\sim\!$图16 。
图14
图15
图16
由图14 $\sim\!$图16 可知,钢芯铝绞线接续管在25%额定拉断力下表现出的振幅最大值为1.54 mm,与线夹出口处的钢芯铝绞线的振幅值1.36 mm较为接近。
4.3 25%额定拉断力下的内嵌式钢芯铝绞线接续管疲劳应变分析
在设定钢芯铝绞线25%额定拉断力为终端张力下,每振动500万次采集一次接续管及管口绞线在疲劳试验机振动下的应变值,直至接续管管口出现明显断裂,在试验结束后,分析接续管及管口绞线的应变变化情况。
结构振动次数为500万次时,接续管及管口绞线在高频疲劳试验机的应变情况如图17 所示。
图17
由图17 可知,接续管管口绞线应变在$4.582 8\times10^{-4}$与$-6.362 5\times10^{-4}$之间变化,有效应变值为$5.025 4\times10^{-4}$;接续管管体应变在$2.563 6\times10^{-4}$与$-3.892 3\times10^{-4}$之间变化,有效应变值为$3.053 2\times10^{-4}$。管口绞线有效应变值为管体应变的1.65倍。
结构振动次数为1000万次时,接续管及管口绞线在高频疲劳试验机的应变情况如图18 所示。
图18
由图18 可知,接续管及管口绞线未出现明显裂纹,接续管管体应变有效值为$3.892 5\times10^{-4}$,接续管管口绞线应变有效值为$7.035 6\times10^{-4}$,为管体的1.81倍。
结构振动次数为1500万次时的接续管及管口绞线应变情况如图19 所示。
图19
由图19 可知,尽管管口绞线出现了细微裂纹,但接续管并未出现明显的宏观裂纹。接续管管体有效应变值为$4.138\times10^{-4}$,管口的绞线有效应变值为管体的2.16倍。
高频疲劳试验机振动为2000万次时接续管及管口绞线的应变情况如图20 所示。
图20
由图20 可知,在振动2000万次时接续管管口绞线出现裂纹,管口绞线的应变有效值达到了$1.208 32\times10^{-3}$,应变值产生跳跃且变化明显快于前期的振动。管口的绞线有效应变值约为管体的2.4倍。
结构振动次数为振动2500万次时,接续管及管口绞线应变情况如图21 所示。
图21
由图21 可知,接续管管体也出现了明显宏观裂纹,管口绞线有效应变值为管体的2.37倍。结构在振动2 869万次时管口绞线出现明显断裂,达到$2.032 14\times10^{-3}$。试验结果表明,结构在振动2 869万次时管口绞线出现明显断裂,结束试验后,接续管管体应变有效值可达到$8.162 4\times10^{-3}$,管口绞线的有效应变阶段与断裂阶段的计算模型吻合。
4.4 接续管表面裂纹与疲劳寿命分析
振动次数达到500万次时,接续管管体及管口绞线均未出现明显损伤,管口绞线表面呈现出细微的裂纹源且萌生磨损,随着载荷的循环,裂纹源将萌生裂纹,从而会出现损伤现象,如图22 所示。
图22
振动次数达到1 000万次时,管口绞线萌生长度不足1 mm的细微裂纹,断裂损伤随着载荷的循环而加速,SEM扫面图如图23 所示。
图23
振动次数达到1 500万次时,管口绞线产生长度为1 mm左右的明显裂纹,接续管没有明显的损伤,随着载荷循环,放射区的疲劳损伤加速,从而形成新的断裂纹,如图24 所示。
图24
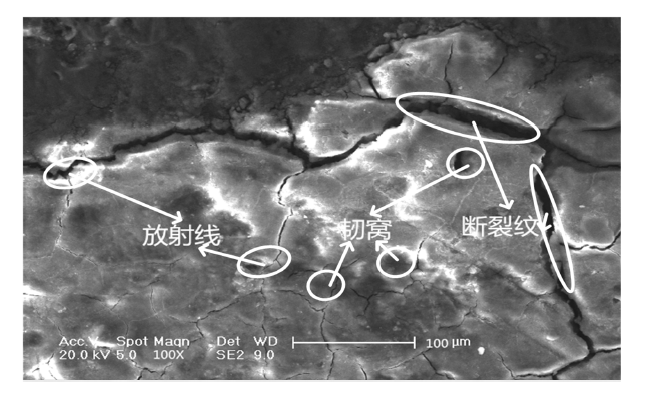
次数达到2 500万次时,裂纹区的深度加深且裂纹扩展速度加快,裂纹长度可达到8 mm,垂放射条纹细且较短,结构呈现韧性断裂,如图25 。
图25
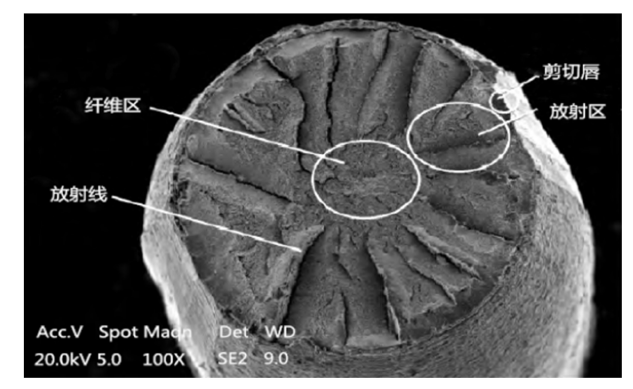
振动次数累积到2 869万次时,结构基本破坏。裂纹断口呈不规则状,断口边缘出现细微的微孔,为裂纹扩展到中心的韧性破坏,如图26 。
图26
5 结论
为了对内嵌式钢芯铝绞线接续管振动疲劳寿命进行研究,以LGJ-240/30钢芯铝绞线接续管为研究对象,根据现有数学模型建立接续管压接风振疲劳响应并求解,然后进行接续管疲劳仿真计算,最后进行接续管疲劳试验,该文主要结论如下:
(1) 通过对内嵌式钢芯铝绞线接续管不同张力下的风振响应仿真分析,得出导线张力从15%额定拉断力到25%额定拉断力变化时,应变有效值从$1.863\times10^{-4}$增加到$4.162\times10^{-4}$;且管体及其他段绞线要远远小于管口绞线的应力应变。
(2) 在不同压接条件下,内嵌式钢芯铝绞线接续管表现出不同的疲劳响应,在压接对边尺寸25.5 mm $\sim$ 31.16 mm区间内,应变值随着压接对边尺寸的增大呈现减小的趋势,且在30 mm时出现疲劳源区域响应谷值,在31 mm和31.16 mm时呈现增大的趋势。
(3) 随着载荷循环次数的增加,接续管管体及绞线的应变值逐渐上升,管口绞线应变由振动500万次增加到2 500万次时,有效应变值从$5.025 4\times10^{-4}$增加到$1.428 36\times10^{-3}$,接续管管体应变由振动500万次增加到2 500万次时,应变有效值从$3.053 2\times10^{-4}$增加到$6.032 8\times10^{-4}$。
(4) 内嵌式钢芯铝绞线接续管可有效降低接续管疲劳源区在微风振动作用下形成的动弯应力,降低导线的疲劳损伤。
参考文献
View Option
[1]
赵隆 , 张甜 , 黄新波 等 . 智慧导线路接续管状态实时感知技术研究
高压电器 , 2020 , 56 (9 ):114 -121, 128
[本文引用: 1]
Zhao Long Zhang Tian Huang Xinbo . et al . Research on real-time state sensing technology of smart transmission line connector
High Voltage Apparatus 2020 , 56 (9 ):114 -121, 128 (in Chinese)
[本文引用: 1]
[2]
熊捷 . 架空高压导线路通电温变微风振动疲劳寿命研究
[硕士论文]. 南昌: 南昌大学 , 2019
[本文引用: 1]
Xiong Jie . Study on fatigue life of high voltage overhead conductor with temperature variable breeze vibration
[Master Thesis]. Nanchang: Nanchang University , 2019 (in Chinese)
[本文引用: 1]
[3]
徐建坤 . 架空导线微风振动强化换热效应及疲劳寿命分析
[硕士论文]. 郑州: 郑州大学 , 2019
[本文引用: 1]
Xu Jiankun . Enhanced heat transfer effect and fatigue life analysis of overhead conductor under aeolian vibration
[Master Thesis]. Zhengzhou: Zhengzhou University , 2019 (in Chinese)
[本文引用: 1]
[4]
陈鑫 . 极寒环境下输电导线的疲劳特性研究
[硕士论文]. 北京: 华北电力大学 , 2019
Chen Xin . Study on fatigue characteristics of overhead transmission lines in extremely cold enviroment
[Master Thesis]. Beijing: North China Electric Power University , 2019
[5]
李林 . 输电导线的微动磨损接触分析及微动疲劳研究
[硕士论文]. 武汉: 华中科技大学 , 2017
Li Lin . A thesis submitted in partial fulfillment of requirements for the degree of master of engineering
[Master Thesis]. Wuhan: Huazhong University of Science and Technology , 2017
[6]
司伟杰 , 黄新波 , 赵隆 等 . 输电导线微风振动疲劳损伤机理
广东电力 , 2017 , 30 (4 ):108 -114
[本文引用: 1]
Si Weijie Huang Xinbo Zhao Long . et al . Mechanism of aeolian vibration fatigue damage of transmission lines
Guangdong Electric Power 2017 , 30 (4 ):108 -114 (in Chinese)
[本文引用: 1]
[7]
王景朝 , 徐乃管 . 复合交变应力条件下的导线疲劳试验方法
电力建设 , 2001 , 22 (2 ):18 -20
[本文引用: 1]
Wang Jingchao Xu Naiguan . Fatigue test method of conductor under compound alternating stress
Electric Power Construction 2001 , 22 (2 ):18 -20 (in Chinese)
[本文引用: 1]
[8]
李黎 , 孔德怡 , 龙晓鸿 等 . 导线微风振动的CFD数值仿真
全国结构工程学术会议, 武汉 , 2008
[本文引用: 1]
Li Li Kong Deyi Long Xiaohong , et al . Numerical simulation of transmission line aeolian vibations by CFD
National Structural Engineering Academic Conference, Wuhan , 2008
[本文引用: 1]
[9]
孔德怡 . 基于动力学方法的特高压导线微风振动研究
[硕士论文]. 武汉: 华中科技大学 , 2009
[本文引用: 1]
Kong Deyi . A thesis submitted in partial fulfillment of the requirements for the degree of doctor of engineering
[Master Thesis]. Wuhan: Huazhong University of Science and Technology , 2009
[本文引用: 1]
[10]
彭添 , 谢强 , 张歌 等 . 微风振动下导线的响应及振动防治
广东电力 , 2017 , 30 (8 ):104 -108
[本文引用: 1]
Peng Tian Xie Qiang Zhang Ge . et al . Response and vibration prevention of conductors under breeze vibration
Guangdong Electric Power 2017 , 30 (8 ):104 -108 (in Chinese)
[本文引用: 1]
[11]
任贤达 . 山火过后退火温度对导线力学性能和疲劳寿命的影响
[硕士论文]. 太原: 太原理工大学 , 2018
[本文引用: 1]
Ren Xianda . Effect of Annealing temperature on fatigue life and mechanical properties of wires after mountain fire
[Master Thesis]. Taiyuan: Taiyuan University of Technology , 2018 (in Chinese)
[本文引用: 1]
智慧导线路接续管状态实时感知技术研究
1
2020
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
智慧导线路接续管状态实时感知技术研究
1
2020
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
架空高压导线路通电温变微风振动疲劳寿命研究
1
2019
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
架空高压导线路通电温变微风振动疲劳寿命研究
1
2019
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
架空导线微风振动强化换热效应及疲劳寿命分析
1
2019
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
架空导线微风振动强化换热效应及疲劳寿命分析
1
2019
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
输电导线的微动磨损接触分析及微动疲劳研究
0
2017
输电导线的微动磨损接触分析及微动疲劳研究
0
2017
输电导线微风振动疲劳损伤机理
1
2017
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
输电导线微风振动疲劳损伤机理
1
2017
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
复合交变应力条件下的导线疲劳试验方法
1
2001
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
复合交变应力条件下的导线疲劳试验方法
1
2001
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
导线微风振动的CFD数值仿真
1
2008
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
导线微风振动的CFD数值仿真
1
2008
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
基于动力学方法的特高压导线微风振动研究
1
2009
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
基于动力学方法的特高压导线微风振动研究
1
2009
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
微风振动下导线的响应及振动防治
1
2017
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
微风振动下导线的响应及振动防治
1
2017
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
山火过后退火温度对导线力学性能和疲劳寿命的影响
1
2018
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...
山火过后退火温度对导线力学性能和疲劳寿命的影响
1
2018
... 作为连接导线的重要金具,接续管在振动和热作用下发生的形变会影响导线路径安全[1 -2 ] .导线的疲劳特性研究主要基于Miner理论,该理论认为损伤的累积造成了导线的疲劳损伤[3 -6 ] .王景朝等[7 ] 基于Miner准则与Wohler安全边界曲线,研究并总结了导体疲劳寿命的估计方法.文献[8 ,9 ]采用有限元方法分析了钢芯铝绞线在不同振幅和不同张力下的动态弯曲应变.然而,由于导线风振响应的复杂性,数值模拟与实际存在较大的差异.文献[10 ,11 ] 研究了微风振动作用下,沿导线方向上电机的疲劳寿命,并根据实时监测数据得到不同环境下导线的损伤特性.综上,国内外学者对微风振动条件下导线的疲劳损伤进行的研究,证明了Miner疲劳准则和Wohler安全边界曲线与疲劳寿命的计算密切相关.目前对疲劳寿命的研究存在如下问题:(1)仅注重线夹的出口端,而忽略了接续管的影响;(2)对接续管失效的研究仍处在对失效金具的表象分析,仅仅提出了压接条件是影响接续管使用的重要因素,并没有对接续管的使用应力进行深层次的研究.为了解决以上问题,本文对接续管的使用应力进行深度分析,提出新型输电导线内嵌式接续管,建立钢芯铝绞线接续管压风振疲劳响应数学模型,将接续管的疲劳破坏划为损伤阶段与断裂阶段,采用COMSOL仿真软件建立相同物理模型进行疲劳仿真计算,通过试验进行接续管疲劳寿命损伤特性研究,并明确压接对边尺寸、压接模长、接续管口倒角型式等压接因素以及风振疲劳对接续管失效的影响. ...