振动力学是力学专业本科生的主干课程之一,也是一门与机械、航空航天、土木等工程密切联系的基础课。通过本课程的学习,有助于学生认识自然和工程中的振动现象,掌握工程结构的振动规律,提高分析问题、解决问题的能力;有助于培养辩证唯物主义的世界观和方法论,为解决工程振动问题和从事科学研究工作打下坚实基础^[1]。

数值模拟借助有限元、边界元等数值方法,依靠计算机,通过数值计算和图像显示,达到认识和解决实际问题的目的。由于大多数实际问题难以得到精确解,而数值方法不仅能满足计算精度要求,且能够适应各种复杂形状问题的求解,已成为一种应用广泛、十分高效的工程分析手段, 也成为高校工科毕业生必须掌握的一种技术^[2]。

本文基于ANSYS数值分析软件,将数值模拟手段引入到振动力学教学中,将教学过程中难以理解的概念、现象等采用数值分析手段直观地模拟出来,在加深学生对知识理解的同时,培养学生数学建模和运用数值手段分析、解决实际问题的能力,为丰富振动力学课程教学手段进行初步探索^[3]。

“力学类教学质量国家标准”建议振动力学课程理论学时数为48学时。国内力学类专业振动力学课程学时数主要有两类,一类是64学时,另一类是48学时,总体上力学类专业该课程理论学时多数在48学时以上^[4]。我校工程力学本科专业振动力学课程理论授课学时为48学时,主要授课内容包括单自由度系统的振动、多自由度系统的振动、振动问题的实用近似解法、连续系统的振动。单自由度体系的振动是多自由度体系振动和连续系统振动的基础,多自由度体系振动的核心内容是振型的概念以及振型叠加法,连续系统的振动是多自由度系统振动的延伸。工程中多数振动问题可采用线性振动理论解决,本科阶段对振动力学知识的掌握对学生未来解决工程振动问题或从事科学研究意义重大^[5]。

振动力学理论抽象,公式推导严谨,要求学生具有很好的数学和力学基础。传统的教学方法过于偏重理论知识的传授,普遍存在以下几方面的问题：(1)教学模式单一,枯燥的理论学习难以活跃课堂气氛;(2)学生对于振动力学中大量的物理概念缺乏直观、形象的认识,难以激发学生的学习热情;(3)理论与工程实践联系不够紧密,学习过程中理论计算与数值模拟的对比分析不够。针对以上问题,借助于数值模拟软件将数值分析结果引入到振动力学课程教学中,可以将晦涩难懂的振动力学概念、现象等通过数值手段直观模拟展示出来,有效激发学生的学习兴趣,提高学生运用数值手段解决实际问题的能力,培养具有创新思维和创造能力的高素质创新型力学人才^[6-7]。

我校工程力学专业本科生开设了数值分析软件ANSYS必修课程。振动力学课程教学中,将一些知识点提取出来,让学生用ANSYS软件进行模拟,并与可能的理论结果进行对比,不仅可以加深学生对知识点的领悟,同时对学生实际操作能力和创新能力的培养也大有裨益。下面列举一些实际教学中利用数值软件模拟振动力学问题的典型实例。

单自由度系统是最简单的振动系统,但其分析方法和结论对多自由度系统和连续系统的分析具有重要的指导意义。单自由度系统固有频率$\omega_{0}=\sqrt{{k}/{m}}$是系统的固有参数。由公式可知,固有频率$\omega_{0}$与系统的等效刚度$k$成正比,与等效质量$m$成反比。为了说明此问题引入如下例题。

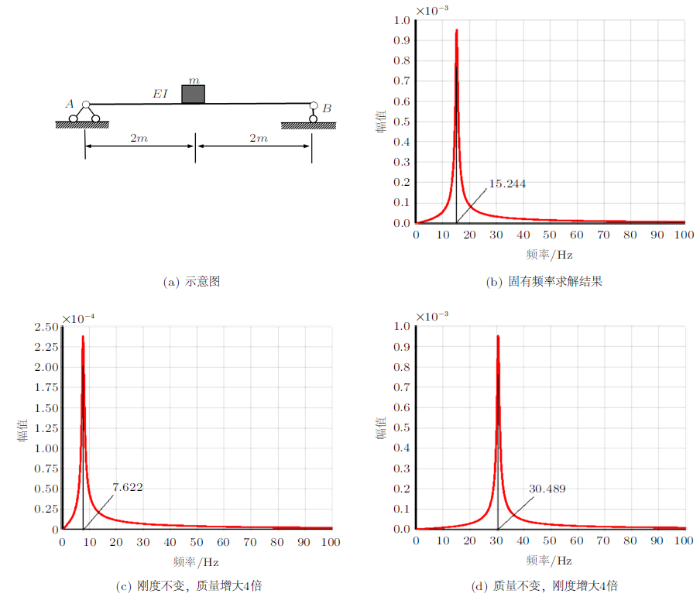
如图1(a)所示,简支梁的抗弯刚度$EI=3.66\times10^{5}$N$\cdot$m$^{2}$,跨中重物固定质量$m=30$kg,不计梁自重,试用ANSYS建模计算其自由振动的固有频率,并试算单独增大质量或刚度时,系统固有频率的变化。

本题理论计算等效刚度为$k={48EI}/{4^{3}}=274.5$ kN/m,固有频率为$\omega =15.244$Hz。数值建模时需将简支梁密度设置为零,以实现梁零自重。本题无论建模还是计算都比较简单,学生容易上手,图1(b)$\sim$图1(d)为 数值模拟结果。从计算结果可知,本题自由振动固有频率模拟结果为15.244 Hz,与理论解一致;当仅质量增大4倍时,固有频率由15.244Hz降低到7.622Hz,正好减小了一倍;当仅刚度增大4倍时,固有频率由15.244Hz提高到30.489Hz,正好增大了1倍,与固有频率求解公式结果一致。因此,对一些等效质量和等效刚度不明显的单自由度系统,采用数值模拟手段确定其固有频率非常有效。

无阻尼振动是一种理想情况,实际振动系统总是有阻尼的。单自由度系统在简谐激励下的受迫振动是动力学中的一个经典内容。下面以质量$-$弹簧$-$阻尼系统为例,说明有阻尼单自由度系统受迫振动情况。

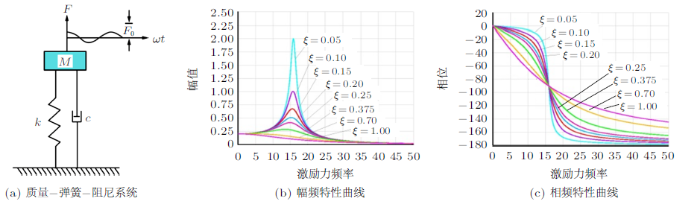
如图2(a)所示,质量$-$弹簧$-$阻尼系统受简谐激励力$F=F_{0} \sin \omega t$作用,其中$M=1$ kg,$k=10$kN/m,$F_{0}=2$kN,$\omega$为激励力频率,$c$为阻尼系数,试绘制不同阻尼比$\xi ={c}/({2\sqrt {kM}})$下系统的幅频特性曲线与相频特性曲线。

幅频特性曲线以幅值为纵坐标、激励力频率为横坐标;相频特性曲线以相位角为纵坐标、激励力频率为横坐标。本题选用ANSYS中的combin14单元进行建模,将不同阻尼比下对应的幅频特性曲线和相频特性曲线绘制在同一张图内,如图2(b)和图2(c)所示。从图中可以确定系统的共振频率与固有频率,清晰看出幅值与相位随激励力频率和阻尼比的变化规律。本例题在培养学生稍复杂系统数值建模思想的同时,借助计算软件的强大功能,可使得学生更深入理解有阻尼受迫振动现象。

在振动力学中,若将系统的分布质量及分布弹簧和阻尼简化为有限个集中质量及有限个无质量的弹簧和阻尼,该系统即可看作多自由度系统。线性多自由度系统存在与自由度数目相等的多个固有频率,每个固有频率对应于系统的一种特定振型。多自由度系统固有频率和振型的求解是振动力学中的重点内容。

“鞭梢效应”是指结构受地震作用时,其顶部质量和刚度突变部分,在每一个来回的转折瞬间,形成较大速度、产生较大位移的现象。就像农村赶车的鞭子,之所以能够甩响,很重要的一个原因是鞭子端部有一段很细的尾巴(鞭梢),当挥动鞭子的时候,由于鞭梢质量突然减小,使得鞭梢的振幅与速度突然加快,从而引发空气剧烈振动,产生清脆的响声。

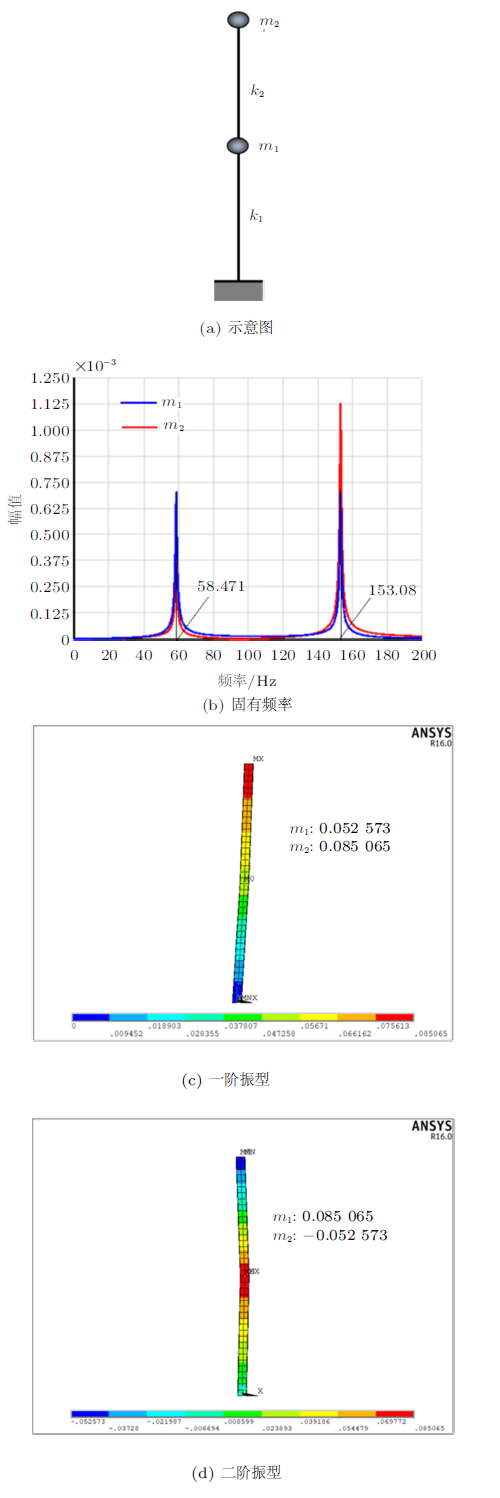
对二层楼房进行固有频率和振型分析时,可采用如图3(a)所示简化模型,假设立柱抗弯刚度$EI=1.43\times 10^{7}$N$\cdot$m$^{2}$,其上等距分布的两个集中质量$m_{1}=m_{2}=100$kg。不计立柱质量,试通过ANSYS软件计算该系统自由振动的固有频率和振型。若二层楼房的顶层为小阁楼时,即$m_{2}$和$k_{2}$突然 减小,假设$m_{2}$和$k_{2}$均减小为原来的1/90时,进一步分析系统振型的变化情况。

本题建模时需注意将质点质量施加在垂直于杆轴的水平方向,即只让质点沿水平方向振动,限定其他两个方向的振动。由图3(b)可知,上下层质量、刚度均相等时,一、二阶固有频率分别为$f_{1}=58.471$ Hz,$f_{2}=153.08$ Hz。由图3(c)和图3(d)知,将$m_{1}$处水平位移转换为1,该模型的一阶振型为$ \xi _{1} =\{ 1.618, \ \ 1\}^{\rm T}$、二阶振型为$ \xi_{2} =\{-0.618,\ \ 1\}^{\rm T}$。可见,上下层质量和刚度相同时,两质点处位移相差不大。

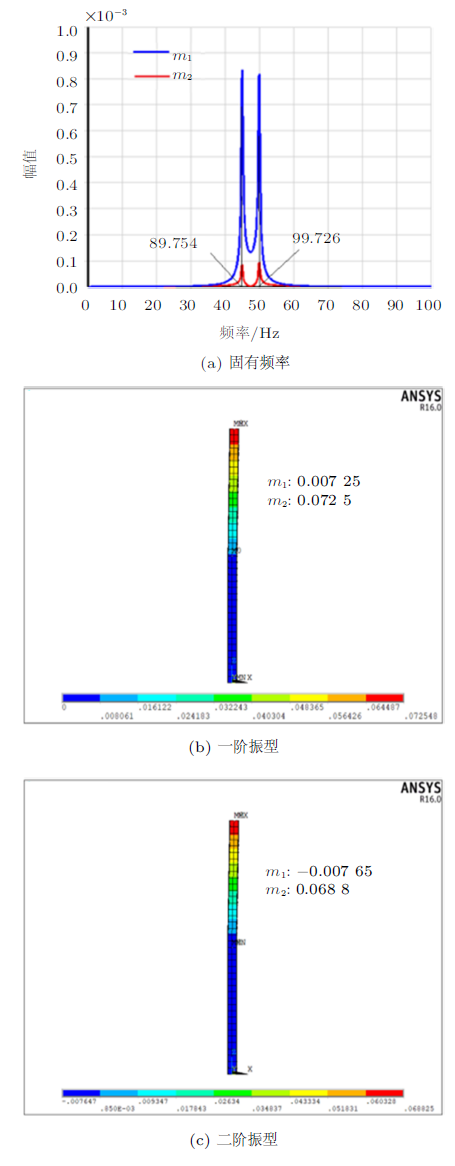
图4为上层$m_{2}$和$k_{2}$均减小为原来的1/90时,固有频率与振型的数值求解结果。从图中可以看出,此时一、二阶固有频率分别为$f_{1}=89.754$ Hz,$f_{2}=99.726$ Hz,一阶振型为$ \xi_{1} =\{ 10,\ \ 1\}^{T}$、二阶振型为$ \xi_{2} =\{-9,\ \ 1\}^{T}$。因此当顶端质点的质量和刚度很小时,顶端水平侧移很大。建筑结构中,因顶端质点质量和刚度突变,而导致顶端巨大反应的鞭梢效应现象实际应用很多。如：屋顶消防水池、上人屋面设计的楼电梯间、女儿墙或等屋顶建筑物。本题介绍了工程中的“鞭梢效应”现象,与工程实际结合紧密,可有效激发学生的探索欲望。

受迫振动是指系统在振动过程中不断受到由外界控制的激励作用。工程中受迫振动的例子很多,比如振动筛、打夯机、医用振荡床等,下面以三层刚架受简谐激励力作用的受迫振动为例进行说明。

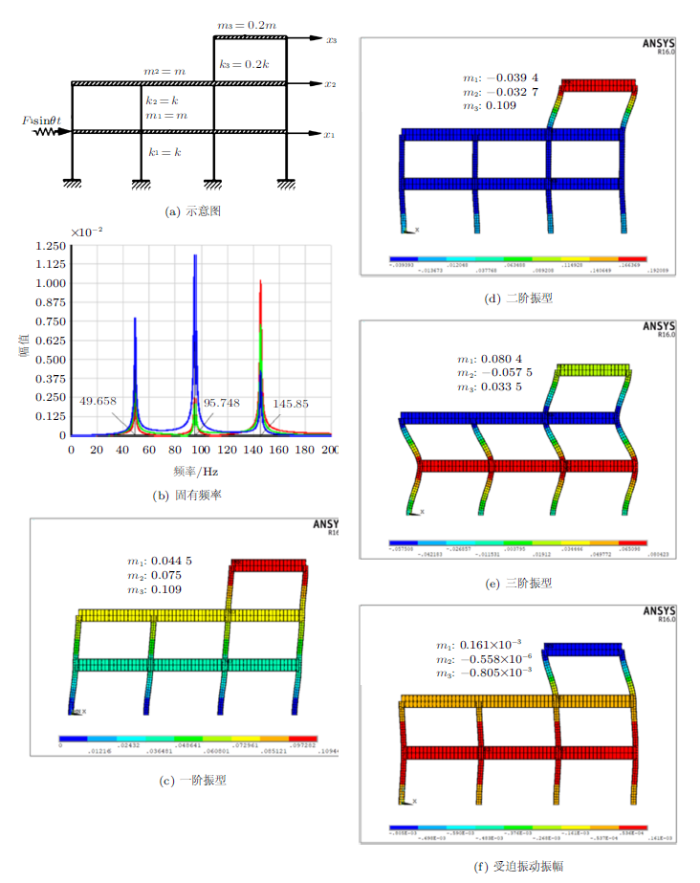
如图5(a)所示三层剪切型刚架系统,横梁的弯曲刚度为无穷大,刚架的全部质量都等效集中到横梁上,分别为$m_{1}=m_{2}=m=100$kg,$m_{3}=0.2m=20$ kg。各层间侧移刚度为$k_{1}=k_{2}=k=3.093\times 10^{4}$ kN/m,$k_{3}=0.2k=0.618\times 10^{4}$ kN/m。在第一层横梁处作用有水平简谐载荷$F(t)=F_{0} \sin \theta t$,其中$F_{0}=100$ kN,$\theta =556.1$rad。试用ANSYS建模计算该系统自由振动的固有频率和振型,并求各层梁受迫振动的振幅。

由图5(b)可知该题前三阶固有频率分别为$f_{1}=49.658$ Hz,$f_{2}=95.748$ Hz,$f_{3}=145.85 $ Hz,其所对应的前三阶振型由图5(c)$\sim$图5(e)所示。该题理论求解时需要写出刚度矩阵、质量矩阵,并求解三元一次方程,求解过程比较繁琐;采用数值模拟手段可快速求得结果,并将振型图直观显示出来,更便于学生对知识点的理解。

图5(f)为受迫振动的振幅图,由图可知$m_{1}$, $m_{2}$, $m_{3}$处的位移比值为1:0:$-$5,因此当稳态振动时,顶层横梁的振幅为底层横梁振幅的5倍,与前面多自由度系统自由振动问题中的理论结果一致。由于顶层质量和刚度发生了突变,产生了“鞭梢效应”,导致顶层产生较大的位移和内力,因此在建筑抗震设计中应尽量避免质量和刚度发生突变。另一方面,刚架在第二层横梁处振幅基本为0,处于静止状态,即顶层对二层横梁有消振作用,工程中可利用。

本例题更接近工程实际,学生表现出了极大的兴趣。本题的练习不仅加深了学生对多自由度系统固有频率、振型和受迫振动的理解,还让学生明白利用所学知识可以切实解决现实工程中的问题,达到了学以致用的效果。

离散系统质点趋于无穷多时就是连续系统,连续系统的很多概念可以从多自由度系统延伸而来。与多自由度系统相比,连续系统自由振动的固有频率从有限个变为无限个,主振型也由原来的向量表示演变为函数表示。采用数值模拟手段对连续系统的振动进行分析,可更加凸显该方法的优越性。

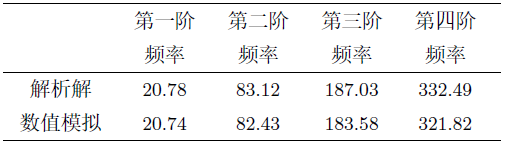
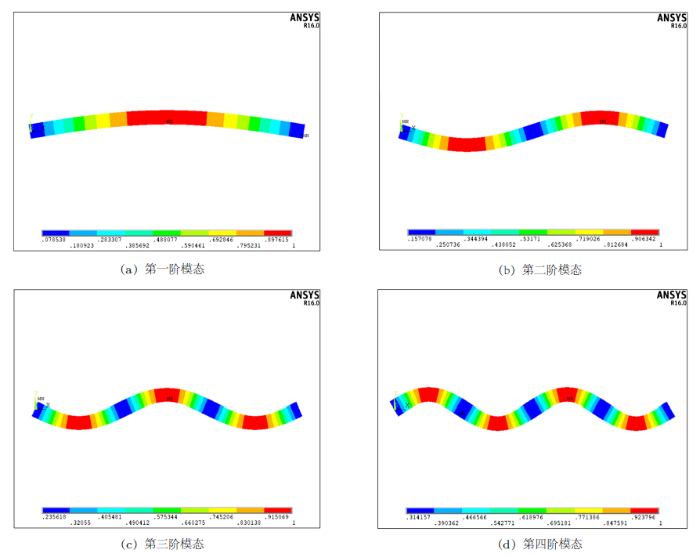
以简支梁固有频率和模态计算为例。某简支钢梁计算跨度$l=8$ m,截面为工字型,截面面积$A=8.337\times 10^{-3}$ m$^{2}$,截面惯性矩$I=2.278\times10^{-4}$m$^{4}$。要求学生用振动力学知识计算该简支梁的固有频率和模态,同时采用ANSYS软件进行建模计算,并将理论计算结果与软件模拟结果进行对比分析。

本题理论求解结果为：固有频率表达式$\omega_{i} =( i\pi/l)^{2}\sqrt{{EI}/({\rho A})}$,模态函数$\varphi_{i} (x)=x\sin ({i\pi }/{l})$,其中,阶数$i=1$, 2,$\cdots$,$E$为钢的弹性模量,$\rho $为钢材密度。采用ANSYS建模计算所得前四阶固有频率与理论结果对比见表1,有限元模拟前四阶模态见图6。

本题理论求解时需要学生掌握无限自由度体系自由振动方程的求解方法,会写边界条件,并能运用数学知识进行方程的推导。由表1对比分析发现,低阶频率误差较小,高阶频率误差较大。可见,对于低阶频率,数值分析完全可以满足精度的要求。同时通过图6可以更直观地了解简支梁前四阶模态形式。

课堂教学中,学生对本题的参与度和积极性非常高,课程结束后基本都能掌握有关简支梁自由振动的知识点,且在建模过程中加深、拓展了学生对所学软件的应用能力。

将数值模拟应用到振动力学课程教学中,在教师的启发下,学生可通过理论学习,利用数值模拟软件实现对振动力学规律的探索。教师在教学过程中可着重引导学生总结规律、提炼结论,由单向知识传授转变为基于解决问题的互动式教学,学生可由被动继承知识为主的学习转变为对未知事物的主动求索,从“知识本位”上升到“能力本位”。

振动力学课程教学结合数值模拟在力17011-2班共56名学生中进行了实践,得到了学生的认可。问卷调查显示：学生总体较满意的比率占到了约90%;学生认为自己理论联系实践能力得到提高的比率为65.5%,分析解决问题能力得到提高的比率为77.6%,自主学习能力得到提高的比率为72.8%,团队协作能力得到提高的比率为69.3%。将应用前后的2016级与2017级学生成绩分析对比列于表2。由表2可知,2017级学生成绩总体优秀率提高了1%,良好率提高了21.83%,中等率提高了2.18%,及格率下降了14.28%,不及格率下降了10.72%,学生总体成绩明显提高。

可见,将数值模拟手段应用到振动力学课程教学中,充分调动了学生学习的积极性与主动性,增加了教师和学生间、学生和学生间的互动性,有效促进了学生发散思维能力和协作交流能力的培养,提高了教学质量,取得了良好的教学效果。通过本课程的学习和训练,可进一步加强学生的数学 建模和利用数值模拟手段解决复杂振动问题的能力。

教学方法的革新是一个长期而艰巨的任务,一门课程教学内容和教学方法的完善需要通过教学实践不断锤炼、不断增补。本文探索了数值模拟手段在我校工程力学专业振动力学课程教学中的应用。振动力学课程教学中结合数值模拟,可有效激发学生的学习兴趣,活跃课堂气氛,并充分践行 “以学生为中心”的教育理念,有效培养学生的创新思维和实践能力。