实际结构均为有限刚度,但为了简化计算,常假定结构体系中某些杆件或杆件沿某个方向为无限刚性,如结构力学教学时常假定杆件的抗压刚度$EA \to \infty $、抗弯刚度$EI \to \infty$^[1-2]。在经典位移法教学中,刚性杆的存在可减少结构体系的基本未知量个数,有利于课堂教学和手算。但对于复杂结构,常难以确定结构的独立结点位移。在矩阵位移法教学时,可以通过计算机编程分析结构内力,如结构力学求解器^[3]。结构分析时,无穷刚度可用大数代替,理论上大数取值越大越接近真解。但受计算机浮点数精度限制,大数不宜取值过大,否则会出现病态方程,导致错误结果。

应用位移法分析刚架时,常假设结构发生微小位移,且不考虑轴向变形和剪切变形对结点位移的影响,即受弯直杆两端结点的距离在结构变 形前后保持不变^[4-6]。有侧移刚架的内力分析,是结构力学的重要教学内容^[7]。对于含斜杆的有侧移刚架存在非独立结点位移,是 结构力学教学的难点内容,若斜杆$EI\to \infty$,将更加难于分析。本文通过分析刚性杆单元的约束方程,确定结构体系的独立结点位移,应用位移法分析结构内力。

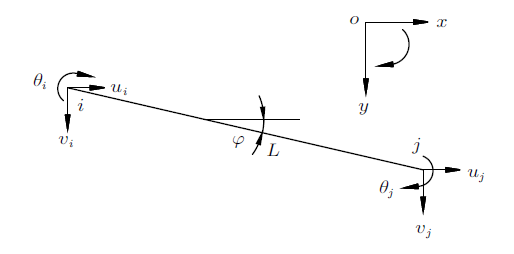
对于一般平面杆单元,在不考虑约束的情况下,每个杆端有3个位移,即水平线位移$u$、竖向线位移$v$和转角位移$\theta$。平面杆单元有2个杆端,共6个杆端位移,如图1所示。位移法分析时,规定以顺时针为正,建立如图1所示整体坐标系。图1中,$u_{i}$,$v_{i}$,$\theta _{i}$分别为杆单元始端的水平位移、竖向位移和转角位移,$u_{j}$,$v_{j}$,$\theta_{j}$为杆单元相应的终端位移,$\varphi$为杆单元与$x$轴的夹角,$L$为杆长。

对于一般杆单元,忽略哪个方向的位移,即认为在该方向是无限刚性。例如刚架常忽略轴向变形,类似于一根刚性链杆约束,即$EA\to \infty $。本文主要考虑$EA\to \infty $和$EI\to \infty $两种情况。

(1) $EA\to \infty $

杆单元无轴向变形,则单元始端的水平线位移和竖向线位移沿杆轴方向的投影必定等于单元终端的水平线位移和竖向线位移沿杆轴方向的投影,其约束方程为

(2) $EI\to \infty $

不考虑杆单元的弯曲变形,则杆单元只能发生刚体转角,杆单元任意两点的转角相等,数值上等于杆端法线方向的相对线位移除以杆长,其约束方程为

在不考虑杆单元约束的情况下,假定所有的杆端位移总数为$n$。若平面杆单元$EA\to \infty $或$EI\to \infty$,由于约束方程的存在,将减少结构体系的独立结点位移个数。将结构体系的所有约束方程联立起来并写成矩阵形式,若系数矩阵的秩为$m$,表示约束方程中有$m$个是独立的,即结构体系有$m$个有效约束。杆端位移总数为$n$,则独立结点位移个数为$n-m$,即为位移法的基本未知量个数。确定基本未知量后,其他的非独立结点位移即可用基本未知量表示。

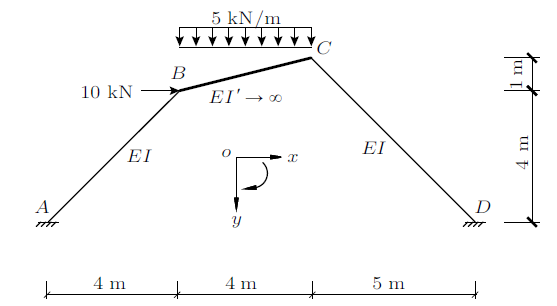
图2所示平面刚架不考虑轴向变形,$AB$杆和$CD$杆的抗弯刚度$EI$为常数,$BC$杆抗弯刚度$E{I}'\to \infty $,应用位移法分析刚架内力并画弯矩图。

将$B$和$C$当作自由结点,则$B$点有水平线位移$u_{B}$、竖向线位移$v_{B}$和转角位移$\theta_{B}$,$C$点有水平线位移$u_{C}$、竖向线位移$v_{C}$和转角位移$\theta_{C}$。因此结构体系的杆端位移总数$n=6$。

对于刚架结构,不考虑轴向变形,即$EA\to \infty $,且$BC$杆抗弯刚度$E{I}'\to \infty $,需根据式(1)和式(2)引入约束方程。

$AB$杆$EA\to \infty $,其约束方程为

令$BC$杆的杆长为$L$,倾角为$\varphi $。$BC$杆$EA\to \infty $,$E{I}'\to \infty $,其约束方程为

将$L=\sqrt {17} $,$\cos\varphi ={4}/{\sqrt {17} }$,$\sin\varphi =-{1}/{\sqrt {17} }$代入式(4),得

$CD$杆$EA\to \infty $,其约束方程为

将式(3)、式(5)和式(6)联立,可得约束方程的矩阵形式

经计算,约束方程系数矩阵的秩$m=5$,即结构体系有5个独立约束方程,因此结构体系只有1个独立结点位移。取$u_{B} $为位移法基本未知量$\varDelta $,则$v_{B} =\varDelta $,$u_{C} =0.6\varDelta$,$v_{C} =-0.6\varDelta $,$\theta_{B} =-0.4\varDelta $,$\theta_{C} =-0.4\varDelta $。

根据转角位移方程,可得

$\begin{eqnarray*} \left. {\begin{array}{l} M_{AB} =-\dfrac{23\sqrt 2 }{80}EI\varDelta, \\[3mm] M_{BA} =-\dfrac{31\sqrt 2 }{80}EI\varDelta, \\[3mm] F_{{\rm Q}BA} =\dfrac{27}{160}EI\varDelta, \\ \end{array}} \right. \ \ \left.{\begin{array}{l} M_{CD} =-\dfrac{29\sqrt 2 }{125}EI\varDelta \\[3mm] M_{DC} =-\dfrac{19\sqrt 2 }{125}EI\varDelta \\[3mm] F_{{\rm Q}CD} =\dfrac{48}{625}EI\varDelta \\ \end{array}} \right. \end{eqnarray*}$

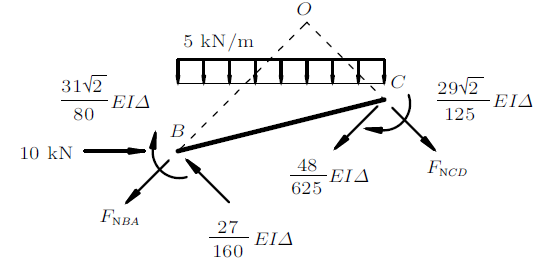
取$BC$杆为隔离体,如图3所示。对$AB$杆和$CD$杆延长线的交点$O$取矩, 解得

$\begin{eqnarray*} \varDelta =\frac{21.398}{EI}\ \ (\to ) \end{eqnarray*}$

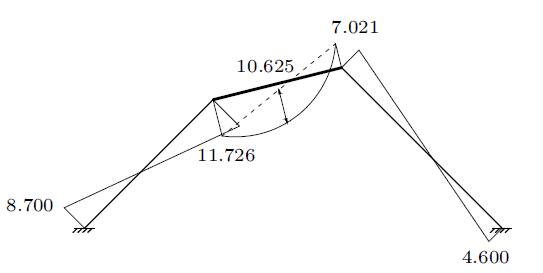
将位移$\varDelta$代入转角位移方程,可计算得到各杆端弯矩。应用叠加法,画出结构的弯矩图,如图4所示。

讨论：若$BC$杆刚度为常量,则$BC$杆仅有轴向约束方程。$AB$杆、$BC$杆和$CD$杆的轴向约束方程彼此独立,因为整个体系有3个独立结点位移。位移法分析时,除$B$点水平位移外,另有$B$点角位移和$C$点角位移2个未知量,因此结构体系共有3个基本未知量。

含刚性杆或刚性约束的结构体系,杆端位移间存在约束关系,将出现非独立结点位移。位移法以独立结点位移作为基本未知量,本文通过引入刚性杆的约束方程,确定含斜杆有侧移刚架的独立结点位移。并根据约束方程,确定非独立结点位移与独立结点位移间的关系式,应用位移法分析结构内力。本方法为精确解法,可作为位移法的补充内容,应用在结构力学教学中。