流体静力学是流体力学授课的重要内容,其研究对象为静止流体与相对平衡流体[1 -2 ] 。在相对平衡液体的铅直分力计算中,教科书和习题解答中一般采用积分进行求解。许多学生觉得计算困难,尤其是涉及到抛物面方程时,积分式非常复杂,学生普遍会出错。实际上,在静止液体作用力求解时,提出了压力体的概念,通过几何作图的方法即可将铅直分力求解出来,可以规避积分过程。教学过程中探索发现,无论是相对平衡液体还是静止液体,求解其对壁面铅直作用力的理论基础和基本方法本质上是相同的,只是等压面形状发生了改变。完全可以将压力体的求解方法引入到相对平衡液体的作用力计算中,以简化计算过程。
1 压力体方法
许多教科书在静水铅直分力的求解过程中,都介绍了压力体及其作图求解方法。压力体的定义为
(1) $\begin{eqnarray} \label{eq1} V_{\rm p} =\iint_{A_{z}} {h{\rm d}} A_{z} \end{eqnarray}$
式中$h$为所求面上微元所处的液下深度,$A_{z}$为曲面沿铅直方向、在自由液面上的投影面。可以看到,压力体仅仅是一种数学上表示的空间体积,该空间由三个面组成,其中所求力的作用壁面已知,故求解关键在于确定其他两个面:自由液面(或延长线)和投影周界面[3 ] 。其中自由液面指压强为大气压的水平面[4 ] 。
铅直分力的大小等于压力体内液体的重力,用压力体体积乘以液体重度即可求得。铅直分力的方向则由压力体与作用液体的相对位置来确定,作用液体指所求壁面接触的液体。当压力体与作用液体处于壁面同侧时,铅直分力方向向下,反之则铅直分力方向向上,可简单记为“同侧向下, 异侧向上”。
2 水平匀加速直线运动液体
水平匀加速直线运动液体与静止液体的区别在于,水平加速度产生了水平质量力,这导致压强不仅沿铅直变化,还会沿水平改变。在一些教科书中,引入铅直淹没深度的概念后,其压强分布规律就统一为[1 ]
(2) $\begin{eqnarray} \label{eq2} p=p_{0} +\rho gH \end{eqnarray}$
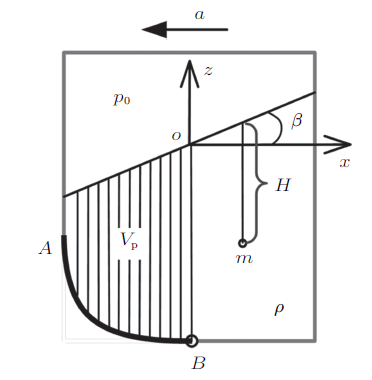
式中,$p_{0}$为液面处压强,$\rho$为液体密度,$g$为重力加速度,$H$为所求压强点的铅直淹没深度,表示该点与向上做铅垂线与自由液面交点之间的距离。对于静止液体,其液面为水平面,当液面为自由面时,式(1)中的$h$就是铅直淹没深度$H$。而匀加速直线运动液体的不同点在于, 其液面为倾斜面(图1 ),当运动加速度为$a$时,倾斜角$\beta$满足
(3) $\begin{eqnarray} \label{eq3} \tan \beta =-\frac{a}{g} \end{eqnarray}$
图1
将静止液体看作加速度为0的匀加速直线运动的特例,两种状态下液体的压强分布规律本质上就没有区别。而两者对壁面的铅直作用力,也同样是采用压强与微元面积乘积在整个壁面上的积分来进行计算。总之,求解的理论基础和基本方法均相同。那么在积分中同样会出现压力体项,只是 水平匀加速直线运动液体的自由液面变为角度为$\beta$的倾斜面而已。
当上部空气为大气压时,液面即为自由面,则任意一点$m$的铅直淹没深度即如图1 中$H$所标识的长度。那么,图中$AB$面上的铅直作用力$F_{AB\rm V}$的大小可采用积分形式计算
(4) $\begin{eqnarray} &&F_{AB\rm V} =\iint_{A_{z} } {p{\rm d}A_{z} }=\iint_{A_{z} } {\rho gH{\rm d}A_{z} }=\\&&\qquad \rho g\iint_{A_{z} } {H{\rm d}A_{z} } \end{eqnarray}$
式中的$\iint_{A_{z}} {H{\rm d}A_{z}}$项即图1 中的阴影部分体积,在考虑自由液面为倾斜面时,这也是压力体的体积。因此,铅直分力也可直接采用压力体内液体重量来计算,其过程变得简单多了。而且,作用力方向同样也可采用“同侧向下,异侧向上”的确定方法。
3 等角速旋转运动液体
当液体做等角速旋转运动时,其等压面变为抛物面,抛物面方程为
(5) $\begin{eqnarray} \label{eq4} z=\frac{\omega^{2}r^{2}}{2g} \end{eqnarray}$
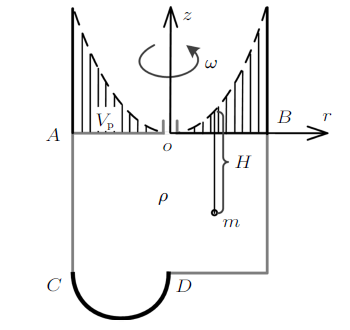
式中,$z$为距抛物面顶点的铅直高度,$\omega$为旋转角速度,$r$为旋转半径,见图2 。
图2
当采用铅直淹没深度作为参数时,其压强分布同样满足式(2),那么在求解壁面上的铅直分力时,其大小同样可由式(4)计算。只是此时的自由液面为压强为大气压且满足式(5)的抛物面。
以流体力学教科书中的经典题目为例,如图2 所示,当容器以角速度$\omega$旋转时,液体对上顶盖的作用力,即可采用上述压力体的方法求解。首先作出自由液面,在这一题中,自由液面并非实际液面,而是过中心点的抛物面(图中虚线所示),将顶板面周界沿铅直方向投影到该抛物面上,所包围的空间即图2 中阴影部分,那么根据“抛物体体积是等底同高圆柱体体积的一半”这一数学结论,即可方便地求得其体积和铅直分力。 而由于压力体在顶板上侧,接触液体在顶板下侧,属于“异侧”,则铅直分力方向向上。
上述结论与教科书中积分获得的结果[1 ] 完全一致,说明压力体的方法也完全适用于等角速旋转运动液体的壁面铅直分力计算,只是此时 自由液面为抛物面而已。而静止液体可以看作角速度为0的旋转运动的特例。
实际教学中,当涉及这种抛物面方程时,许多学生反映积分存在困难,有的直接放弃计算。上述例题中壁面是较为简单的平面,如果壁面为曲面, 如图2 中的$CD$半球面,由于抛物面方程与半球面方程都非常复杂,其积分求解会更为困难,而采用压力体方法则计算会大为简便,学生很容易就能掌握,这更加体现了压力体方法的简便性优势。
4 存在加速度铅直分量的讨论
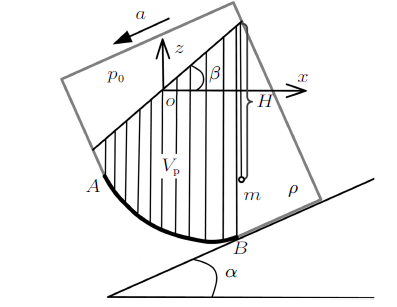
上述两种情况属于加速度仅存在水平分量的情况,当存在加速度铅直分量时,是否仍然可以采用压力体的方式进行求解呢?以经典的坡面下滑匀加速直线运动为例,将装有液体的容器沿倾斜角$\alpha$向下以匀加速度$a$直线运动,如图3 所示,分析$AB$曲面受力。
图3
此时,由于流体存在与运动方向相反的虚构惯性力,其单位质量力分力$f_{x}$和$f_{z}$分别为
(6) $\begin{eqnarray} \left. {{\begin{array}{l} f_{x} =a \cos \alpha \\ {f_{z} =a \sin \alpha -g}\\ \end{array} }} \right\} \end{eqnarray}$
与图1 相比,容器中液体的单位质量力不仅具有$x$方向分量$a \cos \alpha$,在$y$方向上还增加了一个分量$a \sin\alpha$,依据文献[1 ],其等压面方程和静压强分布规律分别为
(7) $\begin{eqnarray} &&\tan \beta =\frac{a\cos \alpha }{g-a\sin \alpha } \end{eqnarray}$
(8) $\begin{eqnarray} &&\label{eq6} p=p_{0} +\rho \left[ {ax\cos \alpha +z\left( {a\sin \alpha -g} \right)} \right] \end{eqnarray}$
(9) $\begin{eqnarray} &&p=p_{0} +\rho \left[ {ax\cos \alpha +z\left( {a\sin \alpha -g} \right)} \right]=\\&&\qquad p_{0} +\rho \left( {g-a\sin \alpha } \right)\left( {\frac{a\cos \alpha }{g-a\sin \alpha }x-z} \right)=\\&&\qquad p_{0} +\rho g\left( {1-\frac{a\sin \alpha }{g}} \right)\left( {x\tan \beta -z} \right)=\\&&\qquad p_{0} +\rho g\left( {1-\frac{a\sin \alpha }{g}} \right)H \end{eqnarray}$
由图3 可知,式中$H$同样是铅直淹没深度。与式(2)相比,式(9)增加了$(1-a\sin\alpha/g$)的乘项,该项反映了加速度铅直分量所引起的重力加速度减小比例,其值小于1,被称为失重系数[1 ] 。而若加速向上运动,则会引起向下的惯性力,相当于重力加速度增加了,该乘项大于1,被称为超重系数。
采用式(9)在$AB$面上积分即可计算该面的铅直受力,其结果为
(10) $\begin{eqnarray} &&F_{AB\rm V}=\rho g\left( {1-\frac{a\sin \alpha }{g}} \right)\iint_{A_{z} } {H{\rm d}A_{z} }=\\&&\qquad\rho g\left( {1-\frac{a\sin \alpha }{g}} \right)V_{\rm p} \end{eqnarray}$
式中的积分项即图中阴影部分体积,故该式仍然可以采用压力体体积的几何方法进行求解,只是加速度的铅直分量改变了重力加速度而已。
5 结语
总之,无论液体作匀加速直线运动还是等角速旋转运动,其壁面铅直分力都可以像静止液体一样采用压力体内液体重量的方法来计算。只是当存在加速度铅直分量时,等效于重力加速度发生了改变,这时需乘以失(超)重系数。力的方向采用“同侧向下,异侧向上”确定。需注意的是,自由液面分别变为倾斜面和抛物面,同学们记忆倾斜面和抛物面的表达式即可。这样计算就变得非常简便了。
教学中先采用积分方法求解,然后引导学生采用压力体来计算,再辅以一些复杂壁面的习题,学生普遍能够领略到压力体求解方法的精妙之处,并且将静力学中的铅直分力计算方法统一记忆,也有助于提高学生的普遍掌握程度。
参考文献
View Option
[3]
高玉清 . “压力体”的绘制”
黑龙江科技信息 , 2008 (12 ): 48
[本文引用: 1]
[4]
辛然 . 水力学中压力体概念浅析
山西科技 , 2015 , 30 (5 ): 43 -45
[本文引用: 1]
Xin Ran . Analysis on the concept of the pressure body in hydraulics
Shanxi Science and Technology 2015 , 30 (5 ): 43 -45 (in Chinese)
[本文引用: 1]
5
2003
... 流体静力学是流体力学授课的重要内容,其研究对象为静止流体与相对平衡流体[1 -2 ] .在相对平衡液体的铅直分力计算中,教科书和习题解答中一般采用积分进行求解.许多学生觉得计算困难,尤其是涉及到抛物面方程时,积分式非常复杂,学生普遍会出错.实际上,在静止液体作用力求解时,提出了压力体的概念,通过几何作图的方法即可将铅直分力求解出来,可以规避积分过程.教学过程中探索发现,无论是相对平衡液体还是静止液体,求解其对壁面铅直作用力的理论基础和基本方法本质上是相同的,只是等压面形状发生了改变.完全可以将压力体的求解方法引入到相对平衡液体的作用力计算中,以简化计算过程. ...
... 水平匀加速直线运动液体与静止液体的区别在于,水平加速度产生了水平质量力,这导致压强不仅沿铅直变化,还会沿水平改变.在一些教科书中,引入铅直淹没深度的概念后,其压强分布规律就统一为[1 ] ...
... 上述结论与教科书中积分获得的结果[1 ] 完全一致,说明压力体的方法也完全适用于等角速旋转运动液体的壁面铅直分力计算,只是此时 自由液面为抛物面而已.而静止液体可以看作角速度为0的旋转运动的特例. ...
... 与图1 相比,容器中液体的单位质量力不仅具有$x$方向分量$a \cos \alpha$,在$y$方向上还增加了一个分量$a \sin\alpha$,依据文献[1 ],其等压面方程和静压强分布规律分别为 ...
... 由图3 可知,式中$H$同样是铅直淹没深度.与式(2)相比,式(9)增加了$(1-a\sin\alpha/g$)的乘项,该项反映了加速度铅直分量所引起的重力加速度减小比例,其值小于1,被称为失重系数[1 ] .而若加速向上运动,则会引起向下的惯性力,相当于重力加速度增加了,该乘项大于1,被称为超重系数. ...
1
2014
... 流体静力学是流体力学授课的重要内容,其研究对象为静止流体与相对平衡流体[1 -2 ] .在相对平衡液体的铅直分力计算中,教科书和习题解答中一般采用积分进行求解.许多学生觉得计算困难,尤其是涉及到抛物面方程时,积分式非常复杂,学生普遍会出错.实际上,在静止液体作用力求解时,提出了压力体的概念,通过几何作图的方法即可将铅直分力求解出来,可以规避积分过程.教学过程中探索发现,无论是相对平衡液体还是静止液体,求解其对壁面铅直作用力的理论基础和基本方法本质上是相同的,只是等压面形状发生了改变.完全可以将压力体的求解方法引入到相对平衡液体的作用力计算中,以简化计算过程. ...
“压力体”的绘制”
1
2008
... 式中$h$为所求面上微元所处的液下深度,$A_{z}$为曲面沿铅直方向、在自由液面上的投影面.可以看到,压力体仅仅是一种数学上表示的空间体积,该空间由三个面组成,其中所求力的作用壁面已知,故求解关键在于确定其他两个面:自由液面(或延长线)和投影周界面[3 ] .其中自由液面指压强为大气压的水平面[4 ] . ...
水力学中压力体概念浅析
1
2015
... 式中$h$为所求面上微元所处的液下深度,$A_{z}$为曲面沿铅直方向、在自由液面上的投影面.可以看到,压力体仅仅是一种数学上表示的空间体积,该空间由三个面组成,其中所求力的作用壁面已知,故求解关键在于确定其他两个面:自由液面(或延长线)和投影周界面[3 ] .其中自由液面指压强为大气压的水平面[4 ] . ...
水力学中压力体概念浅析
1
2015
... 式中$h$为所求面上微元所处的液下深度,$A_{z}$为曲面沿铅直方向、在自由液面上的投影面.可以看到,压力体仅仅是一种数学上表示的空间体积,该空间由三个面组成,其中所求力的作用壁面已知,故求解关键在于确定其他两个面:自由液面(或延长线)和投影周界面[3 ] .其中自由液面指压强为大气压的水平面[4 ] . ...