1 模型与理论推导
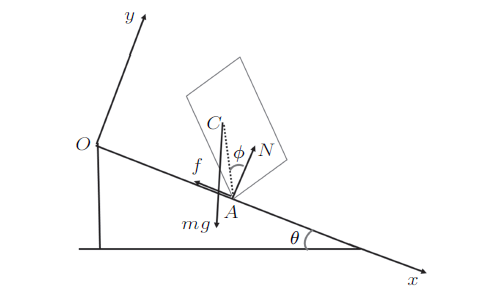
本文讨论带棱角物体一个棱角静止置于斜面上之后将如何运动。如图1所示。设物体质量为$m$,物体质心标记为$C$,物体与斜面只有一个交点,设交点为$A$。物体受到支持力$N$、摩擦力$f$、重力$mg$,这里$g$为重力加速度。设$AC$连线与支持力$N$夹角为$\phi$,并约定$C$位于$A$左侧时,$\phi >0$,$C$位于$A$点右侧时,$\phi<0$。斜面倾角为$\theta$。建立坐标系$xOy$,$x$轴正方向沿斜面向下,$y$轴正方向垂直于斜面向上。物体如果发生转动,即倾倒,设顺时针转动,即物体向斜面下方倾倒,为转动正方向,反之,为转动负方向,物体向斜面上方倾倒。设$AC$长度为$R$,物体相对质心轴的转动惯量可写为$I_{{C}}=mkR^{2}$,$k$由物体具体质量分布而定,比如,对于质量均匀的立方体物体,$k=1/3$。设物体与斜面之间静摩擦系数为$\mu _{{\rm s}}$,动摩擦系数为$\mu_{{\rm k}}$。
图1
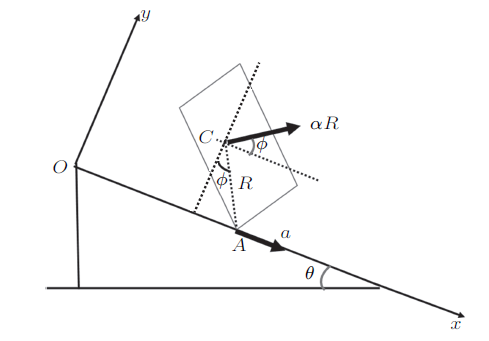
设$A$点沿斜面滑动的加速度为$a$,物体滚动角加速度为$\alpha$,由图2易看出,物体质心加速度的$x$分量$a_{Cx}$和$y$分量$a_{Cy}$分别为
图2
假设物体和斜面都是刚性的,不发生形变,即不考虑滚动摩擦,物体动力学方程为
物体沿斜面滑动有三种情况:不滑动($a=0$);沿斜面向下滑动($a>0$);沿斜面向上滑动($a<0$)。物体倾倒(即物体绕与斜面接触点转动)也有三种情况:不倾倒($\alpha=0$);向下倾倒($\alpha >0$);向上倾倒($\alpha <0$)。物体运动将是滑动和倾倒的组合,总共有九种可能的运动情况。不同的运动情况下,重力和支持力方向不会变化,而摩擦力则不然,摩擦力有三种情况:静摩擦力(方向可能沿斜面向上,也可能沿斜面向下);方向沿斜面向上的动摩擦力(物体向下滑动);方向沿斜面向下的动摩擦力(物体向上滑动)。对此三种情况,下面分别进行讨论。每种情况下,对于滑块的形状和质量分布,又分$\phi \geqslant 0$和$\phi <0$两种情形。
1.1 摩擦力为静摩擦力
物体不滑动,$a=0$,代入式(4),由式(3)$\sim\!$式(5),得
支持力$N$方向只能垂直斜面向上,即总有$N\geqslant 0$。摩擦力为静摩擦力,$\vert f\vert \leqslant \mu_{{\rm s}}N$,其中$\mu _{{\rm s}}$为最大静摩擦系数,方向可沿斜面向上($f>0$)也可沿斜面向下($f<0$)。
1.1.1 $\phi \geqslant 0$
由式(6)可以看出,$N\geqslant 0$自然成立。由式(7)知,$f>0$,由$\left| f \right|=f\leqslant \mu_{{\rm s}}N$,结合式(6)和式(7),得
由式(8)可知,当$\theta =\phi $时,$\alpha=0$,此时物体不滑动也不倾倒,将静止于斜面上;当$\theta >\phi $时,$\alpha >0$,物体将向下倾倒;当$\theta <\phi $时,$\alpha <0$,物体将向上倾倒。
1.1.2 $\phi <0$
由式(8)可知,$\alpha >0$,物体向下倾倒,不可能向上倾倒。由$N\geqslant 0$和式(6),得
由$|f|=f\leqslant \mu_{{\rm s}}N$,结合式(6)和式(7),可得
其中
容易证明,$\tan \theta^{\ast }\leqslant \tan \theta{'}$。
由式(10)$\sim\!$式(13)可知,物体静摩擦力方向平行斜面向上($f\geqslant 0$)或向下($f<0$),体系分别应满足的条件为
和
1.2 摩擦力为方向沿斜面向上的动摩擦力
摩擦力为$f=\mu_{{\rm k}}N$,代入式(4),然后由式(3)$\sim\!$式(5),得
体系应满足条件$a\geqslant 0$和$N\geqslant 0$。下面对$\phi \geqslant 0$和$\phi<0$两种情况分别予以讨论,并讨论$\alpha $的符号。
1.2.1 $\phi \geqslant 0$
由$N\geqslant 0$,结合式(16),得
由$a\geqslant 0$,结合式(17),得
易证明函数
$\begin{eqnarray*} f(\tan \theta )=\dfrac{(k+{\sin }^{2} \phi )\tan \theta +\sin \phi \cos \phi }{k+{\cos }^{2} \phi +\sin \phi \cos \phi \tan \theta } \end{eqnarray*}$
是$\tan \theta$的增函数,并有
$\begin{eqnarray*} &&f(0)=\lt(\dfrac{k}{\sin \phi\cos \phi }+\cot \phi )^{-1}=\mu {'}\\ &&f(\tan \phi )=\tan \phi\\ &&f\lt(\tan \frac{\pi}{2})=\dfrac{k}{\sin \phi \cos \phi }+\tan \phi =\mu^{{\ast}} \end{eqnarray*}$
所以,只要式(20)成立,式(19)自动成立。
由$\alpha =0$和式(18),并结合式(19)和式(20),得物体不发生倾倒的条件为
由$\alpha >0$和式(18),并结合式(19)和式(20),得物体向下倾倒的条件为
由$\alpha <0$和式(18),并结合式(19)和式(20),得物体向上倾倒的条件为
1.2.2 $\phi <0$
由式(16)知,$N\geqslant 0$自动成立。由式(18)可知,$\alpha >0$一定成立,即此时物体只可能向下倾倒。
由$a\geqslant 0$,结合式(17),得
如果$k+{\cos}^{2}\phi +\sin \phi \cos \phi \tan \theta \leqslant 0$,即$\tan \theta \geqslant -{k}/({\sin \phi \cos \phi})-\cot \phi =\tan \theta{'}$, $a\geqslant 0$成立。如果$\tan \theta <\tan \theta{'}$,$a\geqslant 0$,则要求
$\begin{eqnarray*} \mu_{{\rm k}}\leqslant \dfrac{\left( k+\sin^{2}\phi \right)\tan \theta +\sin {\phi \cos \phi }}{k+\cos^{2}\phi +\sin {\phi \cos {\phi \tan \theta }}}=f(\tan \theta ) \end{eqnarray*}$
总之,下滑的物体不会向上倾倒,只可能会向下倾倒,条件是$\tan \theta \geqslant \tan \theta{'}$或$\tan \theta <\tan \theta {'}$且
$\begin{eqnarray*} \mu_{{\rm k}}\leqslant \dfrac{\left( k+\sin^{2}\phi \right)\tan \theta +\sin {\phi \cos \phi }}{k+\cos^{2}\phi +\sin {\phi \cos {\phi \tan \theta }}} \end{eqnarray*}$
1.3 摩擦力为方向沿斜面向下的动摩擦力
摩擦力为$f=-\mu_{{\rm k}}N$,将式(16)$\sim\!$式(18)三式中的$\mu_{{\rm k}}$换成$-\mu_{{\rm k}}$,即是此时动力学方程的解
体系还应满足条件$a\leqslant 0$和$N\geqslant 0$。
1.3.1 $\phi \geqslant 0$
由式(26),$a\leqslant 0$不可能成立,即物体不可能上滑。
1.3.2 $\phi <0$
由$N\geqslant 0$和式(25),得
由$a\leqslant 0$和式(26),得
这里$\theta{'}$和$\theta^{\ast }$分别满足式(12)和式(13)。
由式(12)和式(13)易证明$\theta^{\ast }<\theta{'}$,所以$\theta$与$\theta^{\ast }$和$\theta{'}$的大小关系为$\theta <\theta^{\ast }<\theta{'}$或$\theta^{\ast}<\theta <\theta{'}$或$\theta^{\ast }<\theta{'}<\theta$,但是,第二种情况与式(29)矛盾,如果是第三种情况,根据式(29),有
这与式(28)矛盾,因此$\theta $与$\theta{'}$和$\theta^{\ast}$二者的大小关系为$\theta <\theta^{\ast }<\theta {'}$。因此,物体做上滑运动的条件是
结合式(31)和式(27),得$\alpha >0$,即物体只可能向下倾倒,不会向上倾倒。
2 运动“相图”
梳理一下上部分的结果,斜面上的带棱角物体在静止释放瞬间的运动是滑动和转动(即物体发生倾倒)的组合,共九种情况,各运动形式的发生条件,列于表1,其中,$\mu_{{\rm s}}$为最大静摩擦系数,$\mu _{{\rm k}}$为动摩擦系数,
$\begin{eqnarray*} &&f(\tan \theta )=\dfrac{(k+{\sin }^{2} \phi)\tan \theta +\sin \phi \cos \phi}{k+{\cos }^{2} \phi +\sin \phi\cos \phi \tan \theta }\\ &&g_{1}\left( \tan \theta\right)=-\left(\dfrac{k}{\sin \phi \cos \phi}+\tan \phi \right)\dfrac{\tan \theta -\tan \theta ^{\ast }}{\tan \theta -\tan \theta{'}}\\ &&g_{2}\left( \tan\theta \right)=\left( \dfrac{k}{\sin \phi \cos \phi}+\tan \phi \right)\dfrac{\tan \theta -\tan \theta^{\ast }}{\tan \theta -\tan \theta{'}} \end{eqnarray*}$
$\theta{'}$和$\theta^{\ast}$表达式分别见式(12)和式(13)。 从表中可以看出,九种运动不是都可以发生的。不可以发生的运动,其实是可以预先判断出来的,基于能量和力矩两个物理量可做出判断。物体不会发生纯上滑运动和上滑上滚运动,否则能量将增加。分析物体关于质心的力矩,可知,$\phi\geqslant 0$的物体不会上滑上倾运动,$\phi<0$的物体不会向上无滑倾倒(即绕接触点的纯转动)或下滑上倾运动。
为更直观起见,做一下运动“相图”。从表1可以看出,最方便的作图方式是,在一定$\phi$下,遍历参数空间($\tan \theta $, $\mu )$。分两种情形$\phi \geqslant 0$和$\phi<0$分别作图。
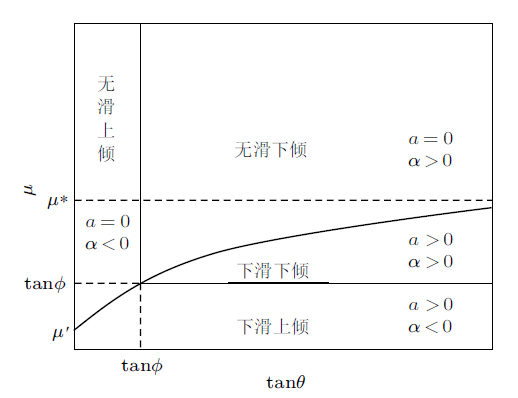
2.1 $\phi \geqslant 0$
$\phi \geqslant 0$时,物体可能的运动情况总结在图3中,摩擦系数$\mu $在$a=0$的区域为最大静摩擦系数$\mu_{{\rm s}}$,否则为动摩擦系数$\mu_{{\rm k}}$。图中$\mu {'}=\bigg( \dfrac{k}{\sin \phi \cos \phi }+$ $\cot \phi \bigg)^{-1}$,$\mu^{{\ast }}=\dfrac{k}{\sin \phi \cos \phi }+\tan \phi$。
图3
当静摩擦系数比较大时,
$\begin{eqnarray*} \mu_{{\rm s}}\geqslant \dfrac{(k+{\sin }^{2}\phi)\tan \theta +\sin \phi \cos \phi}{k+{\cos }^{2}\phi +\sin \phi \cos \phi\tan \theta} \end{eqnarray*}$
物体不会沿斜面滑动,但可以倾倒,斜面倾角比较小(即物体“后仰”程度大)时,$\theta<\phi$,物体向上倾倒,斜面倾角比较大(即 物体“后仰”程度小)时,$\theta>\phi $,物体向下倾倒,$\theta =\phi$时,物体静止于斜面上,显然,这是不稳定平衡。
当动摩擦系数
$\begin{eqnarray*} \mu_{{\rm k}}\leqslant \dfrac{(k+{\sin }^{2}\phi )\tan \theta +\sin \phi \cos \phi }{k+{\cos }^{2}\phi +\sin \phi \cos \phi \tan \theta} \end{eqnarray*}$
物体将边滑边倒,但只会向下滑动,而不会向上滑动。斜面倾角$\theta <\phi$时,物体做下滑上倾运动,斜面倾角$\theta >\phi$时,物体可能下倾也可能上倾,分界线是$\mu_{{\rm k}}=\tan \phi$,此线以上,物体下滑下倾,此线以下,物体下滑上倾。
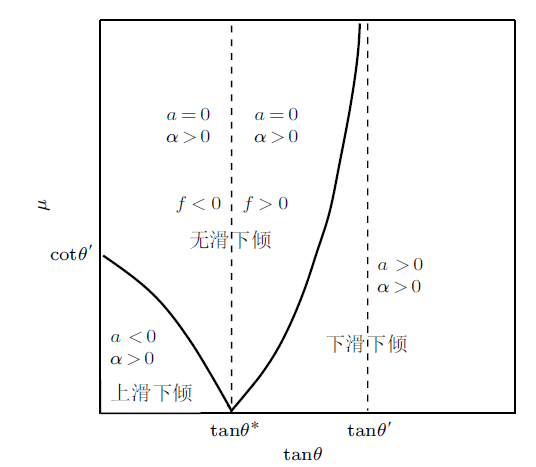
2.2 $\phi<0$
$\phi<0$时,图4总结了物体所有可能的运动情况,摩擦系数$\mu $在$a=0$的区域为最大静摩擦系数$\mu_{{\rm s}}$,否则为动摩擦系数$\mu_{{\rm k}}$。图中$\tan \theta^{\ast}=-\left( \dfrac{k}{\sin \phi \cos \phi }+\tan \phi\right)^{-1}$, $\tan \theta{'}=-\dfrac{k}{\sin \phi\cos \phi }-\cot \phi $。
图4
物体不会向上倾倒,这是符合直觉的,物体重心靠前,只会向下倾倒。
当斜面倾角比较大时,$\tan \theta \geqslant \tan \theta {'}=-{k}/$$(\sin\phi\cos \phi )-\cot \phi $,物体必定向下滑动,与摩擦系数无关。
当斜面倾角比较小,$\tan \theta <\tan \theta^{\ast }=-[{k}/(\sin$ $ \phi$ $ \cos$ $ \phi) +$ $\tan \phi]^{-1}$,且摩擦系数比较小,
$\begin{eqnarray*} \mu_{{\rm k}}<\dfrac{\tan \theta^{\ast }-\tan \theta}{\tan \theta{'}-\tan \theta }\cot \theta^{\ast} \end{eqnarray*}$
此时,物体向下倾倒的同时向上滑动。
当$\tan \theta <\tan \theta^{\ast }$且
$\begin{eqnarray*} \mu_{{\rm s}}>\dfrac{\tan \theta^{\ast }-\tan \theta }{\tan \theta{'}-\tan \theta }\cot \theta^{\ast } \end{eqnarray*}$
时,物体不滑动,静摩擦力方向沿斜面向下,即物体有向上滑动的趋势。当$\tan\theta^{\ast }<\tan \theta <\tan \theta{'}$,且
$\begin{eqnarray*} \mu_{{\rm s}}\geqslant \dfrac{(k+{\sin }^{2}\phi )\tan \theta +\sin \phi \cos \phi }{k+{\cos }^{2}\phi +\sin \phi\cos \phi \tan \theta} \end{eqnarray*}$
时,物体有向下滑动的趋势,静摩擦力方向沿斜面向下。
3 结语
带有棱角的物体静止置于斜面上之后物体有丰富的运动形式。
就教学而言,斜面上带棱角物体运动比球或圆柱运动有三个优势:一是,更接近实际;二是,参数更多,物理内涵更丰富;三是,更具有科研的 味道,方便向学生展示科研—至少是理论研究的过程。物理科学研究中,尤其是理论研究中,通常是对整个参数空间的不同范围对应的不同物理效应给出预言。
作者将此问题用于教学过程取得了很好的教学效果,学生们,尤其是资优学生们,普遍反映深化了对相关知识的理解(刚体动力学)、锤炼了物理直觉(从日常生活经验猜想物体会如何运动)、感受到了探索的乐趣(下滑上倾情形出乎意料)。将本文拓展一下,研究物体有两个棱角或一条边与斜面接触,物体将做何运动,交由学生来做,取得了很好的效果。
本文只讨论了物体被静止释放后瞬间会做何运动,没有讨论物体此后具体的运动过程。物体的运动也有丰富的物理内涵,从偏心圆轮的无滑滚动[4]中可见一斑。
参考文献