一般来说,在理论力学的动力学教学中,绝大部分问题都只需要学生会受力分析、列写动力学方程,并不要求进一步求出具体的运动^[1]。原因之一是绝大部分问题没有解析解,用传统数学方法不好解;原因之二是学时限制,没有更多时间教学生如何求解。

随着计算软件的发展,目前已经可以很轻松地求出动力学方程的解,包括运动和力随时间的变化关系,也可以很容易在屏幕上进行动画演示。

本篇先从动力学中最简单的单摆问题开始介绍：单摆的动力学方程如何求解?数值解的精度如何?大角度情况下周期如何变化?然后介绍椭圆摆的相关问题。

案例1：假设单摆中小球$A$质量为$m$,尺寸不计,绳子$OA$长度为$l$,不计质量(图1)。试比较不同初始角度对运动的影响,以及如何证明计算的结果可靠?

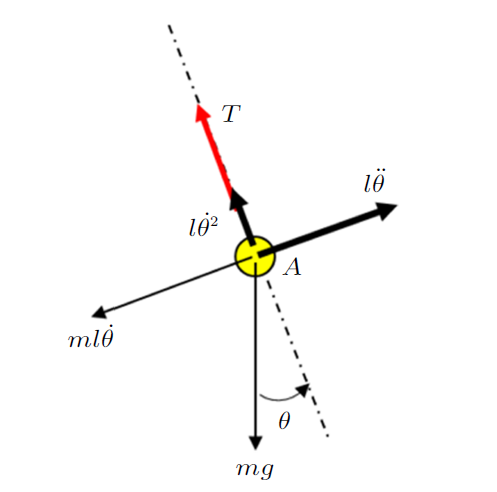
单摆运动时,根据其受力图(图2),可以在切向方向列写系统的动力学方程,为

虽然方程(1)在线性化时有解析解,但是大角度时比较复杂。但在Matlab中,可以直接调用ode45函数统一求解这类常微分方程,其格式是^[3]

其中黑体是固定的格式,斜体是变量或自己命名的函数。其中options是积分的选项,可以控制积分的精度,$'$RelTol$'$表示积分中的相对误差,$'$AbsTol$'$是积分中的绝对误差。在Matlab数值积分计算中,通常$number1$和$number2$可以选为$10^{-8}\sim 10^{-10}$ (精度太高会花费更多计算时间,也没有必要),如果省略则默认为$10^{-3}$。ode45函数则是求解常微分方程的一种常用函数,其中[$t,y$]是积分的时间和结果;动力学方程在子程序$file\_name$中描述; $y0$是初始条件;[$start\_time: step\_time: end\_time$]表示积分时按等步长$step\_time$从开始积分到结束(等步长积分是为了动画演示时每一帧时长相同)。

注意ode45求解标准的一阶常微分方程组,因此要把动力学中的二阶微分方程转换为一阶微分方程组。把方程(1)这样处理：设$y_{1} =\theta$, $y_{2} =\dot{{\theta}}$,得到一阶微分方程组

初始条件为 $y_{1} (0)=\theta (0)$, $y_{2} (0)=\dot{{\theta }}(0)$。

单摆动力学方程求解的源代码见图3,子程序源代码见图4。

主程序源代码中global是表示全局变量,在主程序中赋值后在其他子程序中可以直接调用;plot是画线段的函数,如果很密集,各段微小的线段就构成了曲线;$y(:,1)$表示$y$数组中的第1列,实际上就是每一步计算得到的单摆角度;xlabel和ylabel是给图中坐标轴加上标注,科学论文中一般需要知道坐标是什么含义,什么单位。

子程序用function开头,注意在Matlab中子程序文件名与函数名相同;zeros(2,1)表示生成一个$2\times1$的列阵,里面元素都是0;子程序中的动力学方程直接按照式(3)写出。

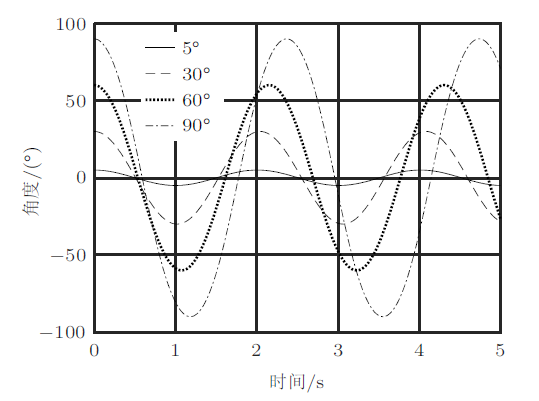
数值计算中初始角度可以变化,其他参数不变,如下所示

图5是方程(1)在不同初始角度下的解(暂时没有考虑空气阻力),可以看到解的周期与初始参数有关,这也是非线性方程的特点。具体计算时可以把不同的初值积分结果赋值给$y1$,$y2$,$y3$,$y4$,在画图plot命令后使用hold on命令可以把不同的曲线叠加在一起;title是给图命名;legend相当于图例,可以给不同的曲线命名以示区别,见图6。

数值计算通常是有误差的,包括数值的截断误差、算法本身的误差等。不过随着计算技术的发展,可显示的最小值越来越小,例如在Matlab中输入realmin($'$single$'$),显示出单精度最小正浮点数为$1.175\,494\,4\times10^{-38}$,所以普通计算精度完全满足要求。

那么方程(1)的数值积分精度如何呢?这首先取决于options中的精度控制,在前面所说的$10^{-8}\sim10^{-10}$情况下,积分计算精度也基本是这一数量级。怎么证明这一点呢?可以通过方程的守恒量来判断。

不考虑空气阻力时,方程(1)有守恒量(机械能)

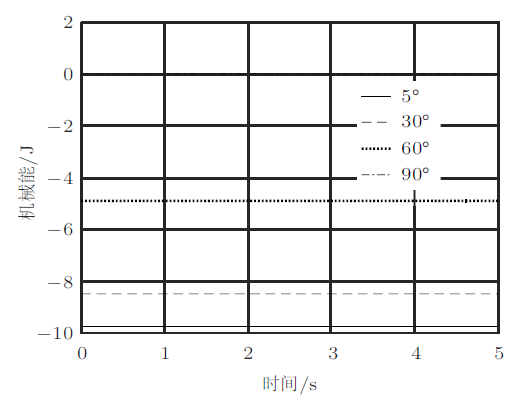
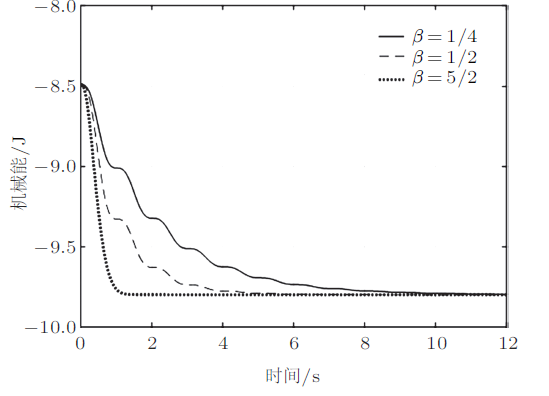
守恒量理论上是一个常数,因此可以用于检测数值计算的可靠性。在数值计算中,可以先把每一步的角度、角速度等量计算出来,然后计算每一步的$E$。考虑到计算有误差,这个“守恒量”应该在极小范围内变化才合理。图7是不同初始条件下方程的积分结果,看起来很平坦,从而证明积分的结果很可靠。

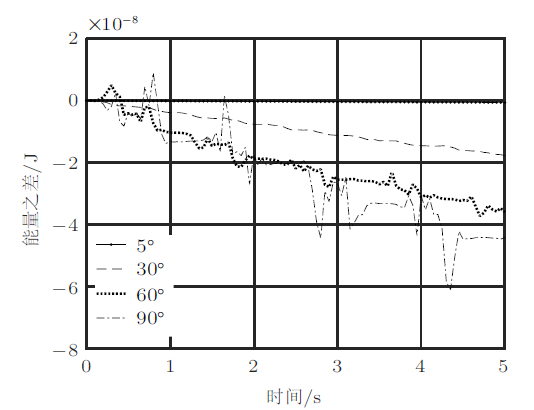
如果想了解积分常数变化的细节,利用能量之差是有效的方法。能量之差定义为

如果没有事先指定等比例(用axis equal命令表示$x$和$y$轴等比例),Matlab在画图时坐标轴会自动根据数据范围进行缩放,因此能量之差的细节变化就可以反映出来(图8),根据能量之差,可以看出系统机械能的变化范围与积分的允许误差范围同阶,初始角度小时计算误差更小。

上述分析表明数值计算是可靠的,然后再考虑系统有阻尼的情况。图9显示了不同阻尼情况下摆角的变化情况,初始摆角均是$30^{\circ}$, 其中$\beta = n/(2m)$是阻尼系数。图10显示了阻尼对系统机械能的影响,最后能量趋于平坦,为系统静止时的机械能。图10中一个细节是：阻尼系数较小时,机械能呈现台阶状的下降,这是因为摆角每次到最大幅值时速度接近,此时空气阻力很小,机械能接近守恒,所以机械能在下降过程中就形成了台阶。

椭圆摆是动力学中的一个典型问题,我们想了解一下：椭圆摆的运动是周期的吗?其周期是多少?

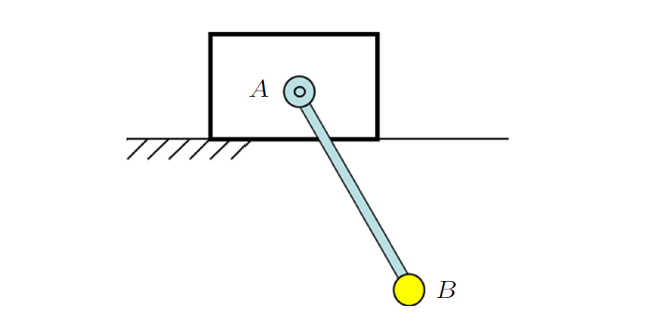
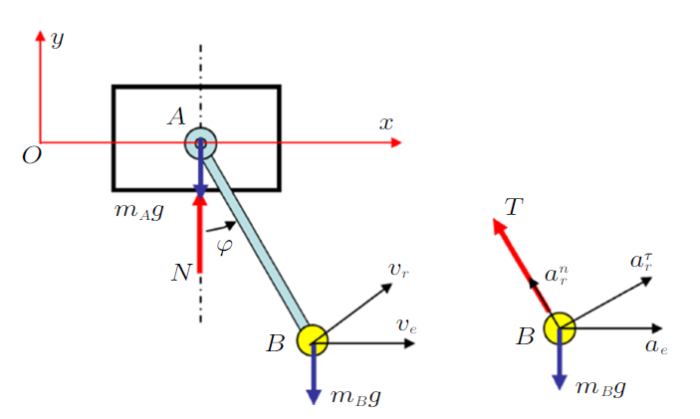
案例2：椭圆摆(图11)由质量为$m_{A}$的滑块$A$和质量为$m_{B}$的单摆$B$构成。滑块可沿光滑水平面滑动,$AB$杆长为$l$,质量不计。试建立系统的运动微分方程,并求水平面对滑块$A$的约束力。

系统有2个自由度,建立$Oxy$坐标系,取$A$点位移$x$和$AB$杆的相对转角$\varphi$为广义坐标(图12),传统分析可得到系统的运动微分方程以及压力的表达式(过程略)为

通常理论力学教材或教学到了这一步就算结束了。椭圆摆在运动过程中$A$滑块和$AB$杆是否为周期运动?是否为正弦运动?压力是如何变化的?类似这样的问题传统方法都不好回答。

系统的运动是周期的吗?在式(7)中消去$\ddot{{x}}$,有

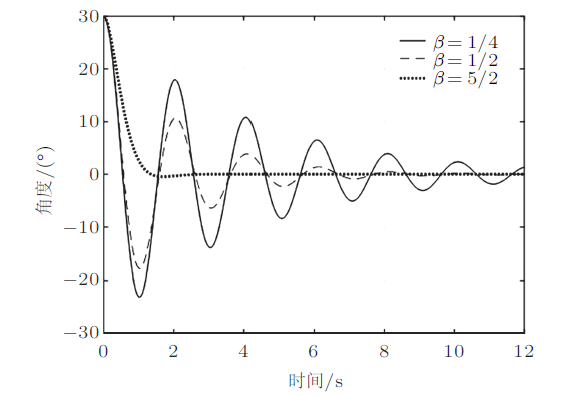
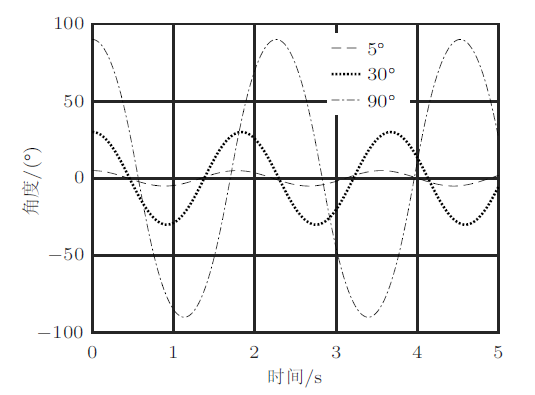
可以看出,摆角的方程(9)在小角度、线性化后是周期的;类比单摆,大角度情况下摆动周期与初始条件有关。下面的计算只改变椭圆摆的 初始角度$\varphi_{0} $,其他参数均不变。

图13显示了初始条件对摆角的影响,看起来不同条件下摆角都是周期函数,但是周期不同。图14进一步显示了周期和初始条件的关系,同时表明：初始角为小量时与线性化的结果比较接近。

图15和图16表明位移和压力也是周期函数,但是初始大角度时位移和压力曲线已经明显偏离标准正弦曲线了。如果没有数值计算,这些细节无法得到。

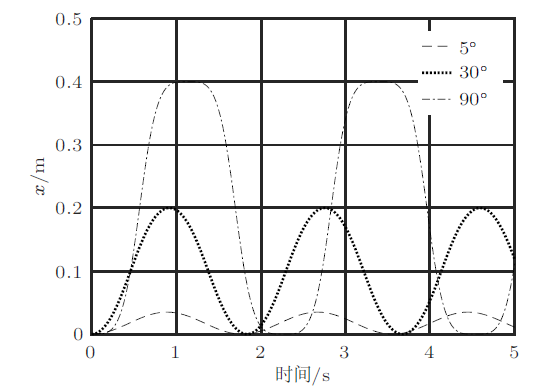
另外还有一个现象,系统的位移、摆角、压力虽然都是周期函数,但是周期并不相同。虽然椭圆摆的摆角看上去像余弦曲线(图13),但是否为标准的余弦曲线?这可以使用快速傅里叶变换来分析。在Matlab中,可以直接调用 fft($data\_name$)函数求出数据$data\_name$的频率。

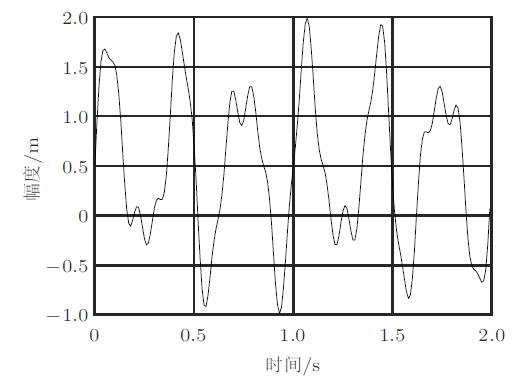
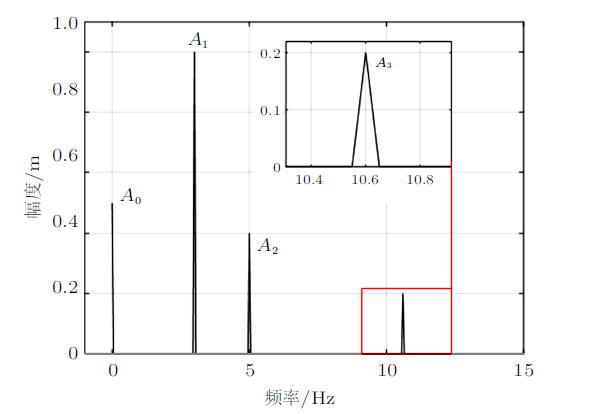
在处理椭圆摆之前,先看看 fft 的效果,设测试函数为

其中$ A_{0}=0.5$, $A_{1} =1$, $A_{2}=0.4$, $A_{3} =0.2$; $f_{1} =3$, $f_{2} =5$, $f_{3} =10.6$,其时域图(图17)看不出什么规律,但经过快速傅里叶变换变化后,在频域图中就可以清楚看出只会在$f=f_{i}$处有一个孤立的峰值$A_{i}$, 而在其他位置均为0：因此在频域图中可以直接得出测试函数(11)中的所有参数(图18)。

下面对椭圆摆的摆角和位移进行快速傅里叶变换变化(位移通过平移去掉直流分量),为了方便比较不同初始条件的结果,把快速傅里叶变换变化后的结果归一化处理：最大值取为1,处理后的结果见图19和图20,可以发现：

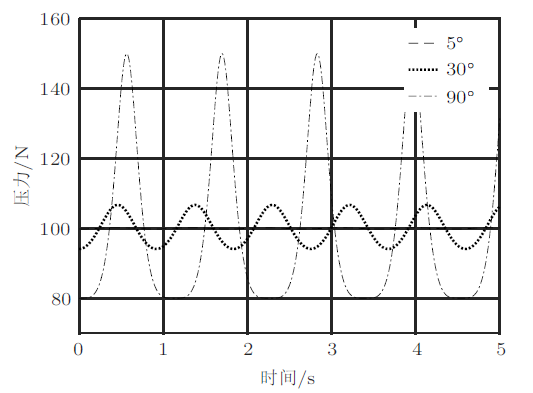
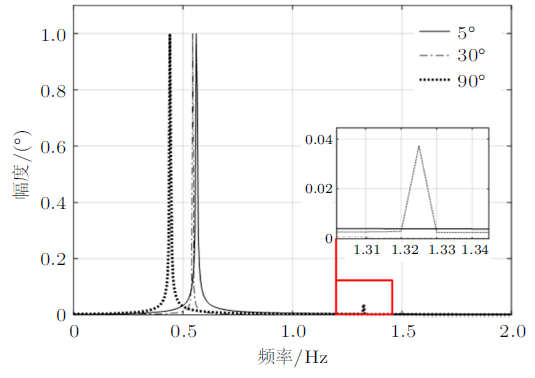
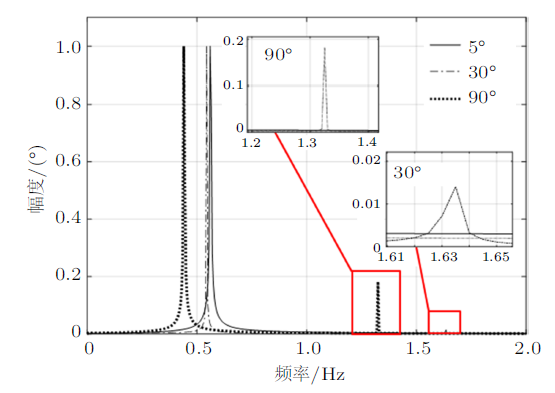
(1)可以看到各条曲线都有一个明显的峰值,但其他位置还有连续的不全为0的值,且大角度时高倍频处还会有小峰值,这说明椭圆摆的摆角不再是标 准的余弦函数;

(2)由于峰值相对明显,所以在时域图中看起来很像余弦曲线;

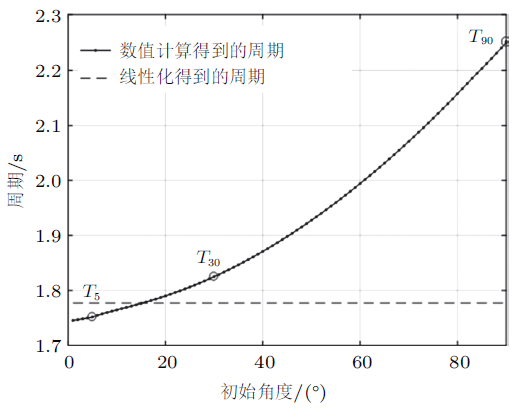
(3)各曲线最大峰值对应的主频率不同：频率随初始角度增加而减少,或周期随初始角度增加而增加,符合图14的结论,这反映了非线性函数的周期或频率与初始条件有关。

现代科学的发展,使得计算的重要性大为提升,它和理论分析、试验验证同为科学研究的三大重要手段。例如,1963年MIT的气象学家Lorenz在计算大气对流问题时发现了混沌现象、现代飞机的设计涉及大量动力学软件的计算,等等。

在这种背景下,在动力学中引入Matlab,除了会列写动力学方程,还能计算和演示系统整个运动过程,便于发现系统丰富的动力学现象。

本篇着重介绍了动力学中运动微分方程的求解,首先把二阶微分方程转换为一阶微分方程组,然后采用荣格库塔法进行求解。涉及到的Matlab核 心函数是 odeset (设置积分精度)和 ode45 (求微分方程);plot和hold on命令可以实现多个图叠在一起。另外介绍了 fft 函数(把时域数据转换到频域),可以分析复杂曲线的频率或周期。

可以看出,借助Matlab可以更加深入地研究动力学问题,解决传统分析方法无法处理的问题。