尾矿作为一种特殊的人工土,与天然土体有很大差异[1 ] 。颗粒沉积特性和分选规律决定着尾矿土的形成过程和工程特性,也影响着尾矿坝的稳定特征。分选和沉积规律受控于尾矿颗粒大小、矿物成分、排放方法以及矿浆浓度 等因素,在多种复杂外力的作用下,形成了不同结构特征和物理力学性质的尾矿堆积体。
尾矿浆流动属于固液两相流动。在稀疏两相流中,尾矿颗粒间的距离较大。颗粒之间、颗粒与流体之间,相互作用力很小,可以忽略[2 ] ;但当超过一定浓度时,颗粒间距离缩小,相互作用力就不能忽略。因此,前者只要承受很小剪切力,流体即发生流动,可视为牛顿流体;后者只有承受剪切力超过一定值,流体才能流动,即为宾汉流体,此剪切力称为屈服剪切力。
本文基于两相流体力学理论,开展了尾矿颗粒在牛顿和非牛顿流体中的沉降和分选规律研究,可为尾矿库放矿管理、勘察、设计等提供客观依据。
1 尾矿颗粒在流体中的受力分析
1.1 第一类作用力(与固$-$流相对运动无关的力)
(1) $\begin{eqnarray} f_{1} =-\frac{1}{6}{\pi}d^{3}\rho_{\rm p}\frac{{\rm d}u_{\rm p} }{{\rm d}t} \end{eqnarray}$
式中,$d$,$\rho_{\rm p} $,$u_{\rm p}$分别为尾矿颗粒的直径、密度及速度。
(2) $\begin{eqnarray} f_{2} =\frac{1}{6}{\pi}d^{3}\rho_{\rm p} g \end{eqnarray}$
(3) $\begin{eqnarray} f_{3} =\frac{1}{6}{\pi}d^{3}\rho_{\rm w} \frac{{\rm d}p}{{\rm d}x} \end{eqnarray}$
式中,${{\rm d}p}/{{\rm d}x}$为压强梯度,若为重力作用引起,则${{\rm d}p}/{{\rm d}x}=g$,该压差力即为浮力;$\rho_{\rm w}$为流体密度。
1.2 第二类作用力(与固$-$流相对运动有关的力)
(4) $\begin{eqnarray} f_{4} =\frac{1}{8}{\pi}c_{\rm p} d^{2}\rho _{{\rm w}} (u_{{\rm w}} -u_{\rm p} )\left| {u_{{\rm w}} -u_{\rm p}}\right| \end{eqnarray}$
式中,$c_{\rm p} $为阻力系数,$c_{\rm p} =({24}/{Re})f(Re)$;$u_{{\rm w}} $为流体速度;$\rho_{{\rm w}}$为流体密度;$f(R{{e}})$为根据不同的雷诺数$Re$进行选择[4 ] :
当取$f(Re)=1$,可解得Stokes阻力公式[4 ]
(5a) $\begin{eqnarray} f_{5a}=3\pi \mu d(u_{\rm w}-u_{\rm p}) \end{eqnarray}$
当取$f(Re)=1+(3/16)Re$,可解得Oseen阻力公式[4 ]
(5b) $\begin{eqnarray} f_{5b}=3\pi \mu d(u_{\rm w}-u_{\rm p})\lt(1+\frac{3}{16}Re) \end{eqnarray}$
如为非球形,需乘以修正系数,可以通过相关手册[5 ] 进行查阅。
(6) $\begin{eqnarray} f_{6} =-\frac{1}{12}{\pi}d^{3}\rho_{\rm w}\lt(\frac{{\rm d}u_{\rm p} }{{\rm d}t}-\frac{{\rm d}u_{{\rm w}} }{{\rm d}t}) \end{eqnarray}$
(7) $\begin{eqnarray} f_{7} =\frac{3}{2}d^{2}\rho_{\rm w} \sqrt {\pi\mu} \int_{t_{0}}^t \frac{\xi (t')}{\sqrt {t-t'} }{\rm d}t^{\prime} \end{eqnarray}$
式中,$\xi (t')$为以前加速度历史的函数,$t_{0} $为启动时间;$\mu$为流体黏度系数。
与固流相对运动垂直的力即侧向力,在一维二相流中不考虑。
(8) $\begin{eqnarray} f_{8} =\frac{1}{8}{\pi}d^{2}\rho_{{\rm w}} c_{\rm L} \lt(u_{{\rm w}} -u_{\rm p}) \end{eqnarray}$
式中,$c_{\rm L} $为升力系数,球形颗粒的$c_{\rm L}$为零,非球形颗粒的$c_{\rm L}$不为零,但由于尾矿颗粒在各方向随机分布,升力互相抵消,因此升力作用可以忽略;$d$为球径。
(9) $\begin{eqnarray} f_{9} =\frac{1}{8}{\pi}d^{3}\omega \rho_{{\rm w}} (u_{{\rm w}} -u_{\rm p} ) \end{eqnarray}$
该力与$\left( {u_{{\rm w}} -u_{\rm p} } \right)$和$\omega$构成右手坐标系。
(10) $\begin{eqnarray} f_{10} =1.62d^{2}\sqrt {\rho_{{\rm w}} \mu } \lt(u_{{\rm w}}-u_{\rm p} )\sqrt {\frac{{\rm d}u_{{\rm w}} }{{\rm d}y}} \end{eqnarray}$
其正负号由$\left( {u_{{\rm w}} -u_{\rm p} }\right){{\rm d}u_{{\rm w}}}/{{\rm d}y}$的符号决定,往往发生在固壁附近,因在固壁附近速度梯度大。
1.3 各种力的作用效果分析
当尾矿浆流动是稳定的,则惯性力$f_{1}$和附加质量力$f_{6}$均为零。同时由于颗粒速度不变,没有相对加速度,因而Basset力$f_{7}$也不存在。即使尾矿浆是非稳定流动,也不是所有的力均同等重要,有必要对以上各力作以量级比较。
(11) $\begin{eqnarray} &&\frac{f_{7}}{f_{5a}}=\frac{d}{2\sqrt {{\pi}\mu} }\frac{1}{u_{{\rm w}} -u_{\rm p} }\int_{t_{0} }^t {\frac{\xi (t')}{\sqrt {t-t'} }{\rm d}t'} =\\&&\qquad\frac{d}{\sqrt {{\pi}\mu} \sqrt {t-t_{0} } }\end{eqnarray}$
(12) $\begin{eqnarray} &&\frac{f_{9}}{f_{5a}}=\frac{1}{24}\frac{\omega d^{2}\rho_{{\rm w}}}{\mu}\\ &&\frac{f_{10}}{f_{5a}}=0.18\sqrt {\frac{d}{u_{{\rm w}} -u_{\rm p} }\frac{{\rm d}u_{{\rm w}} }{{\rm d}y}Re } \end{eqnarray}$
(13) $\begin{eqnarray} &&\frac{f_{10}}{f_{5a}}=0.18\sqrt {\frac{d}{u_{{\rm w}} -u_{\rm p} }\frac{{\rm d}u_{{\rm w}} }{{\rm d}y}Re } \end{eqnarray}$
可见,在初期$[t-t_{0} ]\leqslant 30d^{2}/\mu$时,Basset力$f_7$作用显著;当$\omega d^{2}\gg1$,颗粒旋转很强时,Magnus力$f_9$作用显著;除非流场速度梯度很大,在颗粒尺度范围就变化显著,且$Re$较大,否则Saffman力$f_{10}$影响很小。例如:对于$d\approx 0.1$ mm的颗粒,取$\mu\approx 0.14$ m$^{2}$/s,在$t-t_{0} >20$ $\mu$s时Basset力$f_7$可忽略不计;对于$\omega \approx1400$ r/s的旋转,Magnus力$f_9$可忽略不计;对于${\rm d}u_{{\rm w}}/{\rm d}y<550$ cm/s的速度梯度,Saffman力$f_{10}$可以忽略。
(14) $\begin{eqnarray} &&\hspace{-8mm}\frac{f_{10}}{f_{2}}=3.1\frac{\rho_{{\rm w}} }{\rho _{\rm p} }\sqrt {v\frac{{\rm d}u_{{\rm w}} }{{\rm d}y}} \frac{u_{{\rm w}} -u_{\rm p} }{d}\frac{1}{g}\sqrt 2\qquad \end{eqnarray}$
(15) $\begin{eqnarray} &&\hspace{-8mm}\frac{f_{9}}{f_{2}}=\frac{\dfrac{1}{8}\pi d^{3}\rho_{{\rm w}} \omega (u_{{\rm w}} -u_{\rm p} )}{\dfrac{1}{6}{\pi}d^{3}\rho _{\rm p} g}=\frac{3}{4}\frac{\rho_{{\rm w}} }{\rho_{\rm p}}\frac{\omega (u_{{\rm w}} -u_{\rm p} )}{g} \end{eqnarray}$
显然,要使颗粒在Saffman力$f_{10}$作用下起跳,该力必须大于重力$f_{2}$。此时床面附近流速梯度应大于1230 s$^{-1}$。但是Saffman力$f_{10}$是球形颗粒在均匀无界的均匀剪切流场推出的,只在最大流速梯度的固壁附近,需要考虑。在颗粒跳起后,离固壁距离增加,流速梯度减小,Saffman力$f_{10}$ 也随之减小,小于重力$f_{2}$时颗粒下落。但对于在水中尾矿颗粒旋转时,在同样的速度梯度下将受Saffman力$f_{10}$作用而浮起。
当粒径$d$超过0.01 cm,转动角速度$\omega$达2200 r/s, ${\rho_{\rm p} }/{\rho_{{\rm w}} }=2$时,速度梯度$u_{{\rm w}} -u_{\rm p} $大于1230 s$^{-1}$时,Magnus力$f_{9}$才超过重力$f_{2}$,固体颗粒才能被Magnus力$f_{9}$所托起。
2 在牛顿流体中的沉降和分选
一般颗粒随水流流动的旋转速度均很小,而且除固壁附近外,垂直梯度不大,因此Magnus力和Saffman力对颗粒沉降影响可以忽略不计。固体颗粒沉降是颗粒在垂直流动方向的运动,只是在重力、浮力、绕流层差阻力作用下发生的。
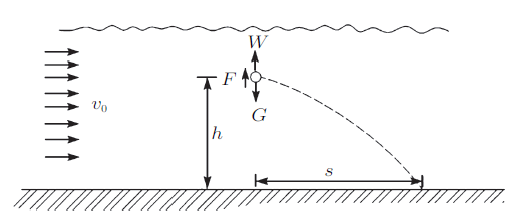
如图1 ,设流体以$v_{0}$的速度作水平层流流动,在离底面$h$处的球形颗粒直径为$d$,水的黏度系数为$\mu$,为牛顿流体,仅考虑在重力$G$、浮力$W$及颗粒运动开始后的绕流压差阻力, 即黏性阻力$F$。颗粒和水的密度分别为$\rho_{\rm p} $和$\rho_{\rm w} $。
图1
(16) $\begin{eqnarray} G-F-W=m\frac{{\rm d}u}{{\rm d}t} \end{eqnarray}$
(17) $\begin{eqnarray} \left. {\begin{array}{l} G=\dfrac{1}{6}{\pi}d_{\rm p}^{3}\rho_{\rm p} g \\ W=-\dfrac{1}{6}{\pi}d^{3}\rho_{\rm w} g \\ F=3{\pi}\mu d_{\rm p} u \\ \end{array}} \right\} \end{eqnarray}$
式中,$u$为沉降速度;$m$为颗粒质量,$m=({\pi d_{\rm p}^{2}}/{6})\cdot$ $\rho _{\rm p} $;$d_{\rm p}$为颗粒直径。
(18) $\begin{eqnarray} &&\frac{{\pi}d_{\rm p}^{3}}{6}\rho_{\rm p} g-3{\pi}\mu d_{\rm p} u-\frac{{\pi}d_{\rm p}^{3}}{6}\rho_{{\rm w}} g=\frac{{\pi}d_{\rm p}^{3}}{6}\rho_{\rm p} \frac{{\rm d}u}{{\rm d}t}\quad \end{eqnarray}$
(19) $\begin{eqnarray} &&\frac{{\rm d}u}{{\rm d}t}+18\frac{\mu }{d^{2}_{\rm p} }u-\lt(1-\frac{\rho _{{\rm w}} }{\rho_{\rm p} })g=0 \end{eqnarray}$
化简初始条件为$t=0$,$u=0$,对微分方程(19)求解得
(20) $\begin{eqnarray} &&u=\frac{\lt(\rho_{\rm p} -\rho_{{\rm w}} )d_{\rm p}^{2}g}{18\mu }-\frac{\lt(\rho_{\rm p} -\rho_{{\rm w}} )d_{\rm p}^{2}g}{18\mu }{\rm e}^{-\dfrac{18\mu }{d_{\rm p}^{2}g\rho_{\rm p} }\displaystyle t}=\\&&\qquad \frac{d_{\rm p}^{2}g\lt(\rho_{\rm p} -\rho_{{\rm w}})}{18\mu }\lt(1-{\rm e}^{-\dfrac{18\mu }{d_{\rm p}^{2}\rho_{\rm p}}\displaystyle t}) \end{eqnarray}$
如沉降距离为$h$,则由式(20)可求得沉降距离$h$与时间$t$的关系式
(21) $\begin{eqnarray} &&\hspace{-4mm}h=\int_0^t u{\rm d}t=\\&&\hspace{-4mm}\qquad \int_0^t {\frac{\lt(\rho_{\rm p} -\rho_{{\rm w}} )d^{2}_{\rm p} g}{18\mu }} \lt(1-{\rm e}^{-\dfrac{18\mu }{d^{2}_{\rm p} \rho_{\rm p} }\displaystyle t}){\rm d}t=\\&&\hspace{-4mm}\qquad \frac{\lt(\rho_{\rm p} -\rho_{{\rm w}} )d^{4}_{\rm p} g\rho_{\rm p} }{324\mu^{2}}\left( {{\rm e}^{-\dfrac{18\mu t}{d^{2}_{\rm p} \rho_{\rm p} }}+\frac{18\mu t}{d^{2}_{\rm p} }-1} \right) \end{eqnarray}$
单个球形颗粒在离床面$h$处的流水中开始沉降的同时,随着水流以流速$v_{0}$一道流动。设水流速为常数,颗粒在水流中扩散作用忽略不计,尾矿颗粒在水中浓度低, 忽略颗粒间的相互作用,则在$t$时间内移动的水平距离$s$为
(22) $\begin{eqnarray} s=\upsilon_{0} t \end{eqnarray}$
据式(21)解出沉降时间$t$,即可得到颗粒沉降时在滩面上分布的位置。但该式是时间$t$的隐式,需用试算法进行反复求解,比较烦琐。分析尾矿颗粒在水中的沉降过程:由于重力大于浮力,开始产生加速沉降,颗粒与流体产生相对速度;初期黏性阻力很小,因而沉降加速度很大;随着时间增加,相对速度和黏性力随之增加;当黏性阻力、重力和浮力接近受力平衡状态,颗粒加速度很小,接近于等速沉降,沉降速度达到极限。为此,令$t\to \infty $,得到最大沉降速度即极限沉降速度
(23) $\begin{eqnarray} u_{\rm t} =\frac{\lt(\rho_{\rm p} -\rho_{{\rm w}})d^{2}_{\rm p}g}{18\mu } \end{eqnarray}$
将整个过程视为以极限速度等速沉降,进行简化计算,则有
(24) $\begin{eqnarray} h= \frac{(\rho_{\rm p} -\rho_{{\rm w}} )d_{\rm p}^{2}g}{18\mu }t \end{eqnarray}$
(25) $\begin{eqnarray} t=\frac{18\mu h}{(\rho_{\rm p} -\rho_{{\rm w}} )d_{\rm p}^{2}g} \end{eqnarray}$
(26) $\begin{eqnarray} s=v_{0} \frac{18\mu h}{(\rho_{\rm p} -\rho_{{\rm w}} )d_{\rm p}^{2}g} \end{eqnarray}$
即流过滩面的固体颗粒,沉积位置与其在流体中位置及流体黏度成正比,与颗粒粒径的平方、颗粒密度与流体密度差成反比。
如果尾矿颗粒形状为非球形,则沉降速度$u_{\rm t1} =\psi u_{\rm t} $,式中,$\psi $为沉降速度的形状系数,按表1 [5 ] 选取;$u_{\rm t} $为等效球形颗粒的沉降速度。
以上所述黏性阻力是假设流体为牛顿体,雷诺数$Re =1$的情况,实验结果与理论结果有很好的近似。当$Re>1$的情况下,由于在Stokes近似中假设迁移项不等于零,在远离物体处,迁移速度将等于自由流速,位移惯性力不能完全不计。 因而在中等$Re$数$10>Re>1$的情况下,应该采用考虑部分位移惯性力影响的Oseen解公式$f_{5b}$计算阻力,然后依次进行以上步骤,得到沉降速度的公式、沉降距离与时间的关系、极限沉降速度、水流中不同粒径在滩面的分布。
3 在尾矿浆中的沉降和分选
3.1 颗粒分选特征研究
设颗粒直径$d_{\rm p} =2r$,浆体为宾汉流体,屈服切应力为$\tau $,颗粒在浆体中受有浮力$W$、重力$G$和剪切阻力$\tau $的作用。设与重力相垂直的微分面积为d$A$,则${\rm d}A={\pi}r^{2}\cos {\rm d}\theta$,设在此微分面上的剪切力为${\rm d}\tau_{\rm B}$,则${\rm d}\tau_{\rm B} =2{\pi}r^{2}\cos^{2}\theta {\rm d}\theta$[8 ] ,$\tau_{\rm B} =\int_{0}^{\pi/2}4{\pi}r^{2}\cos^{2}\theta {\rm d}\theta =4{\pi}r^{2}\int _{0}^{\pi/2} \cos^{2}\theta {\rm d}\theta $。
(27) $\begin{eqnarray} F_{\rm B} =\frac{{\pi}^{2}}{4}d_{\rm p}^{2}\tau_{\rm B} \end{eqnarray}$
(28) $\begin{eqnarray} G=\frac{1}{6}{\pi}d_{\rm p}^{3}\rho_{\rm p} g \end{eqnarray}$
(29) $\begin{eqnarray} W=\frac{1}{6}{\pi}d_{\rm p}^{3}\rho_{\rm m} g \end{eqnarray}$
式中,$\rho_{\rm m}$为浆体密度,即单位时间流过的单位体积的浆体质量$Q_{\rm m} $,即
(30) $\begin{eqnarray} \rho_{\rm m} =\frac{Q_{\rm p} \rho_{\rm p} +Q_{\rm w} \rho_{\rm w} }{Q_{\rm m}} \end{eqnarray}$
式中,$\rho_{\rm p} $为尾矿颗粒密度,kg/m$^{3}$;$\rho_{{\rm w}}$为清水密度,kg/m$^{3}$;$Q_{\rm p}$为尾矿颗粒流量,m$^{3}$/h;$Q_{{\rm w}} $为清水流量,m$^{3}$/h。
颗粒在浆液中不发生沉降时有$G\leqslant W+F_{\rm B} $,由式(28)和式(29),有
(31) $\begin{eqnarray} \frac{1}{6}{\pi}d_{\rm p}^{3}\rho_{\rm p} g\leqslant \frac{1}{6}{\pi}d_{\rm p}^{3}\rho_{\rm m} g+\frac{{\pi}^{2}}{4}d_{\rm p}^{2}\tau_{\rm B} \end{eqnarray}$
(32) $\begin{eqnarray} d_{\rm p0} =\frac{3{\pi}\tau_{\rm B} }{2(\rho_{\rm p} -\rho_{\rm m} )} \end{eqnarray}$
当尾矿颗粒小于$d_{{\rm p0}} $时不发生沉降。由式(32)可见,当屈服应力$\tau_{\rm B} =0$,尾矿浆流体为牛顿体,$d_{{\rm p0}}=0$,即全部尾矿颗粒均可发生沉降。如果屈服应力不等于零时,则小于界限直径的部分尾矿颗粒不发生沉降,即不能分选,大于界限直径的颗粒仍然发生沉降。
设尾矿浆的体积浓度为$C_{\rm v}$,尾矿中小于$d_{\rm p0}$的颗粒含量为$S_0$,此部分颗粒不发生沉降,与水组成为两相流体。则根据定义有
(33) $\begin{eqnarray} &&1 -\frac{\rho_{\rm p} -\rho_{{\rm m}} }{\rho_{\rm p} -\rho_{{\rm w}} }=S_0C_{{\rm v}} \end{eqnarray}$
(34) $\begin{eqnarray} &&\rho_{\rm p} -\rho_{{\rm m}} =\lt(1-S_0C_{{\rm v}} )\lt(\rho_{\rm p} -\rho_{{\rm w}} ) \end{eqnarray}$
(35) $\begin{eqnarray} d_{{\rm p0}} =\frac{3{\pi}\tau_{\rm B}}{2(1-S_0C_{{\rm v}} )(\rho_{\rm p} -\rho_{\rm w} )g} \end{eqnarray}$
可见,$d_{\rm p0}$与浆体屈服应力和尾矿颗粒的体积浓度有关,且屈服应力$\tau_{\rm B}$也随着浓度增加而增大,因而浓度是影响尾矿颗粒浆体沉降中最重要因素。此外,小于界限直径的颗粒含量越大则$d_{\rm p0}$越大,说明$d_{\rm p0}$与粒度级配和尾矿颗粒的密度有关。
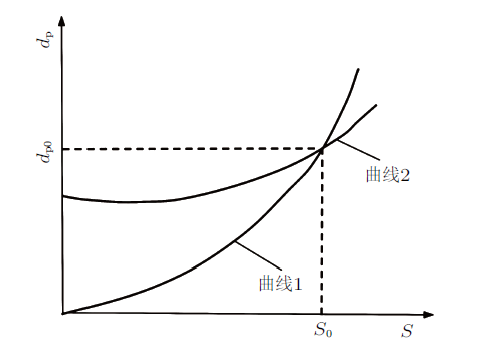
式(35)中有两个未知数$S_0$及$d_{\rm p0}$,需要补充一个方程,才能求解不沉降最大直径$d_{\rm p0}$。为此,可先绘出粒度级配曲线$d_{\rm p}$-$S$ (曲线1),然后据式(35)绘出另一条曲线(曲线2),两曲线的交点坐标即为($S_{0}, d_{\rm p0})$,如图2 所示。
图2
由式(35)可见,浆体分选沉降可分为三种:(1) 浓度较低时:$\tau_{\rm B}=0$,$d_{{\rm p0}}=0$,全部尾矿颗粒均参与,此时载体不含任何尾矿颗粒。一般为清水,称为不稳定浆体。(2) 浓度较高时,$\tau _{\rm B} \ne 0$,$d_{{\rm p0}} >0$,大于$d_{{\rm p0}}$的部分尾矿颗粒参与分选沉降,小于$d_{{\rm p0}}$的颗粒则与水构成新流体,不发生沉降,一般尾矿浆均如此,称为半稳定浆体。(3) 浓度进一步提高时,$\tau_{\rm B} $值很大,$d_{{\rm p0}}$值大于所有尾矿颗粒直径,则浆体中物料不再发生分选沉降,称为稳定浆体。
3.2 颗粒沉降规律研究
不沉的最大颗粒直径$d_{\rm p0} $与$\tau_{\rm B}$有关,即与浆料的浓度有关[9 ] 。浓度小,$\tau_{\rm B}$越小,即分子增大,同时$C_{\rm v}$增大,分母增大,故颗粒不沉直径也减小,同时随浓度中稳定部分所占的比例减小而减小。即原来不沉降颗粒也将有部分发生沉降,随着沉降不断发生,物料浓度降低,不沉颗粒也随之发生沉降,从而使物料浓度 再降低,不沉降物料颗粒进一步降低,直至全部颗粒都发生沉降,这就是浆体沉降的过程。
仍假设物料为球体。在宾汉体中存在屈服应力$\tau_{\rm B}$,在沉降过程中除受到牛顿流体中的重力、浮力及黏性阻力作用外,还受到$\tau_{\rm B} $引起的阻力$F_{\rm B} $,计算公式
(36) $\begin{eqnarray} F_{\rm B} =\frac{{\pi}^{2}}{4}d_{\rm p}^{2}\tau_{\rm B} \end{eqnarray}$
(37) $\begin{eqnarray} &&G-F-F_{\rm B} -W=m\frac{{\rm d}u}{{\rm d}t}\\ \end{eqnarray}$
(38) $\begin{eqnarray} &&\frac{{\pi}}{6}d_{\rm p}^{3}\rho_{\rm p} g-\frac{1}{6}{\pi}d_{\rm p}^{3}\rho_{\rm m} g-3{\pi}\mu d_{\rm p}u-\frac{{\pi}^{2}}{4}d_{\rm p}^{2}\tau_{\rm B} =\\&&\qquad\frac{{\pi}}{6}d_{\rm p}^{3}\rho_{\rm p} \frac{{\rm d}u}{{\rm d}t} \end{eqnarray}$
(39) $\begin{eqnarray} \frac{{\pi}}{6}d_{\rm p}^{3}(\rho_{\rm p}'-\rho _{{\rm w}} )g-3{\pi}\mu d_{\rm p} u =\frac{{\pi}}{6}d_{\rm p}^{3}\frac{{\rm d}u}{{\rm d}t}\rho_{\rm p} \end{eqnarray}$
与球体在牛顿流体中沉降微分方程(18)对比可见,通过当量密度变换,可将宾汉体中的沉降分选问题化为在牛顿流体中的沉降问题,从而2节中颗粒在牛顿流体的沉降及分选公式可以适用,得沉降速度公式
(40) $\begin{eqnarray} u=\frac{d_{\rm p}^{2}g(\rho_{\rm p}'-\rho_{{\rm w}} )\rho _{\rm p} }{18\mu }\lt(1-{\rm e}^{-\dfrac{18\mu }{d_{\rm p}^{2}\rho } t}) \end{eqnarray}$
(41) $\begin{eqnarray} h=\frac{\rho_{\rm p} (\rho_{\rm p}'-\rho _{{\rm w}} )d_{\rm p}^{4}g}{324\upsilon^{2}}\lt({\rm e}^{-\dfrac{18\mu t}{d_{\rm p}^{2}}}+\frac{18\mu t}{d\mbox{p}^{2}}) \end{eqnarray}$
同样,颗粒在沉降的同时,以与水流相同速度$v_{0}$沿沉积滩向前流动,对于分选沉降颗粒粒径不同则沉积在沉积滩不同位置上,有
(42) $\begin{eqnarray} S=v_{0} t \end{eqnarray}$
在宾汉流体中沉降时,其沉速将等于极限速度,这个极限速度称为最终沉速,有
(43) $\begin{eqnarray} u_{\rm t} =\frac{(\rho_{\rm p}'-\rho_{{\rm w}} )d_{\rm p} ^{2}g}{18\mu } \end{eqnarray}$
(44) $\begin{eqnarray} t=\frac{18\mu h}{(\rho_{\rm p}'-\rho _{{\rm w }} )d_{\rm p}^{2}g} \end{eqnarray}$
则在$t$时间内,沉降至底面时颗粒随水流$v_{0}$的水平运移距离为
(45) $\begin{eqnarray}s=v_{0} \frac{18\mu h}{(\rho_{\rm p}'-\rho_{{\rm w}} )d_{\rm p} ^{2}g} \end{eqnarray}$
3.3 结果讨论和验证
尾矿浆浓度按20%考虑[10 ] ,动力黏度$\mu $取500 MPa$\cdot$s;矿浆密度变化范围1.8$\sim$2.0 g/cm$^{3}$,将$\rho' _{\rm p}$取为1.9 g/cm$^{3}$;6种典型尾矿的平均粒径取为[11 ] :$d_{\rm p}$(尾中砂) = 0.35 mm,$d_{\rm p}$ (尾细砂) = 0.20 mm,$d_{\rm p}$ (尾粉砂) = 0.074 mm,$d_{\rm p}$ (尾粉土) = 0.05 mm,$d_{\rm p}$ (尾粉质黏土) = 0.035 mm,$d_{\rm p}$ (尾黏土) = 0.02 mm。据《尾矿库手册》[10 ] 和《尾矿设施设计规范》[11 ] ,尾矿浆输送流速不宜小于1.0 m/s,且矿浆流速达到1.5 m/s以上时管槽不会冻结,为此将计算流速$v_{0}$取为1.5 m/s。
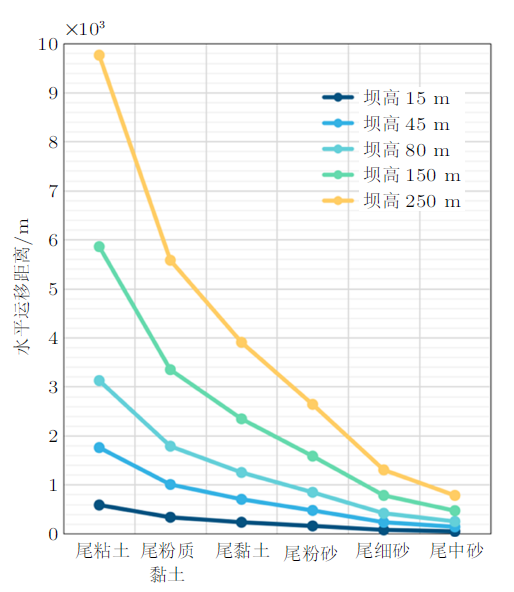
取各等别尾矿库坝高[11 ] 的均值为代表,绘制5个等别尾矿库的尾矿水平运移距离。相应坝高为:15 m (五等库)、45 m (四等库)、85 m (三等库)、150 m (二等库)、250 m (一等库)。根据式(45)绘制水平运移距离$S$变化曲线,如图3 所示。
由图3 可见:(1) 不同等别尾矿库的水平运移距离曲线变化趋势是一致的;(2)随着坝高增加,水平运移距离急剧增大,如尾黏土颗粒运移距离由五等库的585 m增加到9761 m;(3)粒径增加导致水平运移距离减小,而且随着坝高增加,粒径的影响程度愈加显著,如对于坝高250 m的一等库,运移距离由780 m变化到9761 m,说明坝高对尾矿浆沉降和分选产生重大影响。
图3
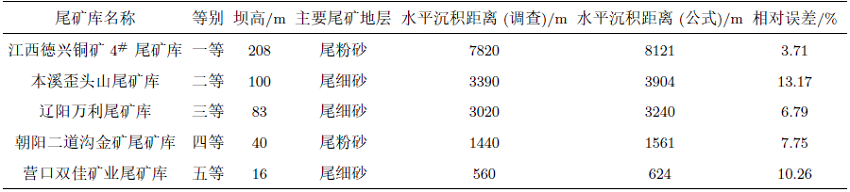
收集国内代表性尾矿库的沉积情况,与理论公式(45)的计算结果进行对比,见表2 。
可见,调查与理论计算结果基本吻合,但略小于理论值。分析原因,应是由其他因素对尾矿沉积过程的影响造成的,如尾矿浆向尾矿库内流动时,随着较大颗粒的沉降导致浓度降低,$\tau_{\rm B}$随之变化,原来不沉的颗粒也会发生沉降;尾矿浆从放矿口排出时,由于浓度高,部分不沉颗粒也跟着一起集体沉降,从而影响尾矿颗粒的输运距离和分布,导致理论计算结果的误差。
4 结论
(1)剖析了尾矿颗粒在浆体中所受的两类作用力。第一类包括惯性力、重力和压差力;第二类包括:沿固$-$流相对运动方向的力(绕流压差阻力、附加质量力和Basset力)和与固$-$流相对运动垂直的力(升力、Magnus力和Saffman力)。
(2)通过与Stokes力比较:在$[t-t_{0} ]\leqslant 30d^{2}$/$\mu$时,Basset力作用显著;当$\omega d^{2}\gg 1$,颗粒旋转很强时,Magnus力作用显著;在流场速度梯度很大,且$Re$较大时,Saffman力作用显著。通过与重力比较,给出了Saffman力与Magnus力的尾矿颗粒起跳判据。
(3)建立了牛顿流体中的尾矿颗粒受力方程,进行了尾矿颗粒的受力特征和沉降特点分析,推导出了尾矿颗粒的最终沉降速度、沉降与距离之间关系式。按等速沉降简化分析,建立了沉降距离与时间关系的解析计算式,对不同$Re$的沉降计算进行了说明。
(4)确定了尾矿颗粒在宾汉型流体中的分选特点,提出固体颗粒在浆体流动中不沉最大粒径的概念,给出不沉最大粒径$d_{\rm p0max}$的表达式及确定方法,分析了不同浓度时浆体分选沉降特征。
(5)推导出宾汉流体中的尾矿颗粒沉降微分方程。通过当量密度与密度的等效变换,得到沉降速度计算公式,并建立沉降距离和时间关系,求得沉降至底面时颗粒随水流的水平移动距离表达式,分析了尾矿浆从放矿口排出后的颗粒沉降特征。
(6)对不同等别尾矿库的不同类别尾矿水平运移规律进行讨论,利用国内代表性尾矿库的尾矿沉积资料数据,得出运移距离的计算相对误差在15%以内,验证了理论公式的可靠性,并对误差原因进行了分析。
参考文献
View Option
[1]
郝喆 , 陈殿强 , 侯永莉 . 尾矿库加高增容稳定性及监测技术研究 . 沈阳 : 东北大学出版社 , 2018
[本文引用: 1]
Hao Zhe Chen Dianqiang Hou Yongli . Study on Stability of Heightening-expanding and Monitoring Technology of Tailings Pond . Shenyang : Northeastern University Press , 2018 (in Chinese)
[本文引用: 1]
[2]
黄朋举 . 颗粒物料下落、反弹和堆积过程的数值模拟. [硕士论文]
西安: 西安建筑科技大学 , 2015
[本文引用: 1]
Huang Pengju . Numerical simulation of falling, rebounding and stacking of granular materials. [Master Thesis]
Xi'an: Xi'an University of Architecture and Technology , 2015 (in Chinese)
[本文引用: 1]
[3]
林雪松 , 陈殿强 , 何峰 . 固液两相流中颗粒浓度分布统一公式的研究
水资源与水工程学报 , 2013 , 24 (4 ): 82 -84
[本文引用: 1]
Lin Xuesong Chen Dianqiang He Feng . Study on unified formula of particle concentration distribution in two-phase flow of liquid-solid
Journal of Water Resources and Water Engineering 2013 , 24 (4 ): 82 -84 (in Chinese)
[本文引用: 1]
[4]
郭烈锦 . 两相与多相流动力学 . 西安 : 西安交通大学出版社 , 2002
[本文引用: 4]
Guo Liejin . Flow Mechanics of Two Phases and Polyphase . Xi'an : Xi'an Jiaotong University , 2002 (in Chinese)
[本文引用: 4]
[5]
涂启华 , 扬赉斐 . 泥沙设计手册 . 北京 : 中国水利水电出版社 , 2006
[本文引用: 2]
Tu Qihua Yang Laifei . Sediment Design Manual . Beijing : China Water Resources and Hydropower Press , 2006 (in Chinese)
[本文引用: 2]
[6]
由长福 , 祁海鹰 , 徐旭常 . Basset力研究进展与应用分析
应用力学学报 , 2002 , 19 (2 ): 31 -33 , 139 -140
[本文引用: 1]
You Changfu Qi Haiying Xu Xuchang . Research progress and application analysis of Basset force
Journal of Applied Mechanics 2002 , 19 (2 ): 31 -33 , 139 -140 (in Chinese)
[本文引用: 1]
[7]
赵万勇 , 李易松 , 王振 等 . 旋流泵中颗粒运动方程的探讨
兰州理工大学学报 , 2007 , 33 (6 ): 47 -49
[本文引用: 1]
Zhao Wanyong Li Yisong Wang Zhen , et al . The study of particle motion equation in swirl pump
Journal of Lanzhou University of Technology 2007 , 33 (6 ): 47 -49 (in Chinese)
[本文引用: 1]
[8]
Davies MP Martin TE . Upstream constructed tailings dam-A review of the basics
The Seventh International Conference on Tailings and Wine Waste, Fort Collins , 2000
[本文引用: 1]
[9]
Hu HH . Direct simulation of flows of solid-liquid mixtures
International Journal of Multiphase Flow 1996 , 22 (2 ): 335 -352
DOI
URL
[本文引用: 1]
[10]
沃廷枢 . 尾矿库手册 . 北京 : 冶金工业出版社 , 2013
[本文引用: 2]
Wo Tingshu . Tailings Pond Manual . Beijing : Metallurgical Industry Press , 2013 (in Chinese)
[本文引用: 2]
[11]
GB50863-2013尾矿设施设计规范 . 北京 : 中国计划出版社 , 2013
[本文引用: 3]
GB50863-2013 Code for Design of Tailings Facilities . Beijing : China Planning Publishing House , 2013 (in Chinese)
[本文引用: 3]
1
2018
... 尾矿作为一种特殊的人工土,与天然土体有很大差异[1 ] .颗粒沉积特性和分选规律决定着尾矿土的形成过程和工程特性,也影响着尾矿坝的稳定特征.分选和沉积规律受控于尾矿颗粒大小、矿物成分、排放方法以及矿浆浓度 等因素,在多种复杂外力的作用下,形成了不同结构特征和物理力学性质的尾矿堆积体. ...
1
2018
... 尾矿作为一种特殊的人工土,与天然土体有很大差异[1 ] .颗粒沉积特性和分选规律决定着尾矿土的形成过程和工程特性,也影响着尾矿坝的稳定特征.分选和沉积规律受控于尾矿颗粒大小、矿物成分、排放方法以及矿浆浓度 等因素,在多种复杂外力的作用下,形成了不同结构特征和物理力学性质的尾矿堆积体. ...
颗粒物料下落、反弹和堆积过程的数值模拟. [硕士论文]
1
2015
... 尾矿浆流动属于固液两相流动.在稀疏两相流中,尾矿颗粒间的距离较大.颗粒之间、颗粒与流体之间,相互作用力很小,可以忽略[2 ] ;但当超过一定浓度时,颗粒间距离缩小,相互作用力就不能忽略.因此,前者只要承受很小剪切力,流体即发生流动,可视为牛顿流体;后者只有承受剪切力超过一定值,流体才能流动,即为宾汉流体,此剪切力称为屈服剪切力. ...
颗粒物料下落、反弹和堆积过程的数值模拟. [硕士论文]
1
2015
... 尾矿浆流动属于固液两相流动.在稀疏两相流中,尾矿颗粒间的距离较大.颗粒之间、颗粒与流体之间,相互作用力很小,可以忽略[2 ] ;但当超过一定浓度时,颗粒间距离缩小,相互作用力就不能忽略.因此,前者只要承受很小剪切力,流体即发生流动,可视为牛顿流体;后者只有承受剪切力超过一定值,流体才能流动,即为宾汉流体,此剪切力称为屈服剪切力. ...
固液两相流中颗粒浓度分布统一公式的研究
1
2013
固液两相流中颗粒浓度分布统一公式的研究
1
2013
4
2002
... 式中,$c_{\rm p} $为阻力系数,$c_{\rm p} =({24}/{Re})f(Re)$;$u_{{\rm w}} $为流体速度;$\rho_{{\rm w}}$为流体密度;$f(R{{e}})$为根据不同的雷诺数$Re$进行选择[4 ] : ...
... 当取$f(Re)=1$,可解得Stokes阻力公式[4 ] ...
... 当取$f(Re)=1+(3/16)Re$,可解得Oseen阻力公式[4 ] ...
... (3) Saffman力[4 ] ...
4
2002
... 式中,$c_{\rm p} $为阻力系数,$c_{\rm p} =({24}/{Re})f(Re)$;$u_{{\rm w}} $为流体速度;$\rho_{{\rm w}}$为流体密度;$f(R{{e}})$为根据不同的雷诺数$Re$进行选择[4 ] : ...
... 当取$f(Re)=1$,可解得Stokes阻力公式[4 ] ...
... 当取$f(Re)=1+(3/16)Re$,可解得Oseen阻力公式[4 ] ...
... (3) Saffman力[4 ] ...
2
2006
... 如为非球形,需乘以修正系数,可以通过相关手册[5 ] 进行查阅. ...
... 如果尾矿颗粒形状为非球形,则沉降速度$u_{\rm t1} =\psi u_{\rm t} $,式中,$\psi $为沉降速度的形状系数,按表1 [5 ] 选取;$u_{\rm t} $为等效球形颗粒的沉降速度. ...
2
2006
... 如为非球形,需乘以修正系数,可以通过相关手册[5 ] 进行查阅. ...
... 如果尾矿颗粒形状为非球形,则沉降速度$u_{\rm t1} =\psi u_{\rm t} $,式中,$\psi $为沉降速度的形状系数,按表1 [5 ] 选取;$u_{\rm t} $为等效球形颗粒的沉降速度. ...
Upstream constructed tailings dam-A review of the basics
1
2000
... 设颗粒直径$d_{\rm p} =2r$,浆体为宾汉流体,屈服切应力为$\tau $,颗粒在浆体中受有浮力$W$、重力$G$和剪切阻力$\tau $的作用.设与重力相垂直的微分面积为d$A$,则${\rm d}A={\pi}r^{2}\cos {\rm d}\theta$,设在此微分面上的剪切力为${\rm d}\tau_{\rm B}$,则${\rm d}\tau_{\rm B} =2{\pi}r^{2}\cos^{2}\theta {\rm d}\theta$[8 ] ,$\tau_{\rm B} =\int_{0}^{\pi/2}4{\pi}r^{2}\cos^{2}\theta {\rm d}\theta =4{\pi}r^{2}\int _{0}^{\pi/2} \cos^{2}\theta {\rm d}\theta $. ...
Direct simulation of flows of solid-liquid mixtures
1
1996
... 不沉的最大颗粒直径$d_{\rm p0} $与$\tau_{\rm B}$有关,即与浆料的浓度有关[9 ] .浓度小,$\tau_{\rm B}$越小,即分子增大,同时$C_{\rm v}$增大,分母增大,故颗粒不沉直径也减小,同时随浓度中稳定部分所占的比例减小而减小.即原来不沉降颗粒也将有部分发生沉降,随着沉降不断发生,物料浓度降低,不沉颗粒也随之发生沉降,从而使物料浓度 再降低,不沉降物料颗粒进一步降低,直至全部颗粒都发生沉降,这就是浆体沉降的过程. ...
2
2013
... 尾矿浆浓度按20%考虑[10 ] ,动力黏度$\mu $取500 MPa$\cdot$s;矿浆密度变化范围1.8$\sim$2.0 g/cm$^{3}$,将$\rho' _{\rm p}$取为1.9 g/cm$^{3}$;6种典型尾矿的平均粒径取为[11 ] :$d_{\rm p}$(尾中砂) = 0.35 mm,$d_{\rm p}$ (尾细砂) = 0.20 mm,$d_{\rm p}$ (尾粉砂) = 0.074 mm,$d_{\rm p}$ (尾粉土) = 0.05 mm,$d_{\rm p}$ (尾粉质黏土) = 0.035 mm,$d_{\rm p}$ (尾黏土) = 0.02 mm.据《尾矿库手册》[10 ] 和《尾矿设施设计规范》[11 ] ,尾矿浆输送流速不宜小于1.0 m/s,且矿浆流速达到1.5 m/s以上时管槽不会冻结,为此将计算流速$v_{0}$取为1.5 m/s. ...
... [10 ]和《尾矿设施设计规范》[11 ] ,尾矿浆输送流速不宜小于1.0 m/s,且矿浆流速达到1.5 m/s以上时管槽不会冻结,为此将计算流速$v_{0}$取为1.5 m/s. ...
2
2013
... 尾矿浆浓度按20%考虑[10 ] ,动力黏度$\mu $取500 MPa$\cdot$s;矿浆密度变化范围1.8$\sim$2.0 g/cm$^{3}$,将$\rho' _{\rm p}$取为1.9 g/cm$^{3}$;6种典型尾矿的平均粒径取为[11 ] :$d_{\rm p}$(尾中砂) = 0.35 mm,$d_{\rm p}$ (尾细砂) = 0.20 mm,$d_{\rm p}$ (尾粉砂) = 0.074 mm,$d_{\rm p}$ (尾粉土) = 0.05 mm,$d_{\rm p}$ (尾粉质黏土) = 0.035 mm,$d_{\rm p}$ (尾黏土) = 0.02 mm.据《尾矿库手册》[10 ] 和《尾矿设施设计规范》[11 ] ,尾矿浆输送流速不宜小于1.0 m/s,且矿浆流速达到1.5 m/s以上时管槽不会冻结,为此将计算流速$v_{0}$取为1.5 m/s. ...
... [10 ]和《尾矿设施设计规范》[11 ] ,尾矿浆输送流速不宜小于1.0 m/s,且矿浆流速达到1.5 m/s以上时管槽不会冻结,为此将计算流速$v_{0}$取为1.5 m/s. ...
3
2013
... 尾矿浆浓度按20%考虑[10 ] ,动力黏度$\mu $取500 MPa$\cdot$s;矿浆密度变化范围1.8$\sim$2.0 g/cm$^{3}$,将$\rho' _{\rm p}$取为1.9 g/cm$^{3}$;6种典型尾矿的平均粒径取为[11 ] :$d_{\rm p}$(尾中砂) = 0.35 mm,$d_{\rm p}$ (尾细砂) = 0.20 mm,$d_{\rm p}$ (尾粉砂) = 0.074 mm,$d_{\rm p}$ (尾粉土) = 0.05 mm,$d_{\rm p}$ (尾粉质黏土) = 0.035 mm,$d_{\rm p}$ (尾黏土) = 0.02 mm.据《尾矿库手册》[10 ] 和《尾矿设施设计规范》[11 ] ,尾矿浆输送流速不宜小于1.0 m/s,且矿浆流速达到1.5 m/s以上时管槽不会冻结,为此将计算流速$v_{0}$取为1.5 m/s. ...
... [11 ],尾矿浆输送流速不宜小于1.0 m/s,且矿浆流速达到1.5 m/s以上时管槽不会冻结,为此将计算流速$v_{0}$取为1.5 m/s. ...
... 取各等别尾矿库坝高[11 ] 的均值为代表,绘制5个等别尾矿库的尾矿水平运移距离.相应坝高为:15 m (五等库)、45 m (四等库)、85 m (三等库)、150 m (二等库)、250 m (一等库).根据式(45)绘制水平运移距离$S$变化曲线,如图3 所示. ...
3
2013
... 尾矿浆浓度按20%考虑[10 ] ,动力黏度$\mu $取500 MPa$\cdot$s;矿浆密度变化范围1.8$\sim$2.0 g/cm$^{3}$,将$\rho' _{\rm p}$取为1.9 g/cm$^{3}$;6种典型尾矿的平均粒径取为[11 ] :$d_{\rm p}$(尾中砂) = 0.35 mm,$d_{\rm p}$ (尾细砂) = 0.20 mm,$d_{\rm p}$ (尾粉砂) = 0.074 mm,$d_{\rm p}$ (尾粉土) = 0.05 mm,$d_{\rm p}$ (尾粉质黏土) = 0.035 mm,$d_{\rm p}$ (尾黏土) = 0.02 mm.据《尾矿库手册》[10 ] 和《尾矿设施设计规范》[11 ] ,尾矿浆输送流速不宜小于1.0 m/s,且矿浆流速达到1.5 m/s以上时管槽不会冻结,为此将计算流速$v_{0}$取为1.5 m/s. ...
... [11 ],尾矿浆输送流速不宜小于1.0 m/s,且矿浆流速达到1.5 m/s以上时管槽不会冻结,为此将计算流速$v_{0}$取为1.5 m/s. ...
... 取各等别尾矿库坝高[11 ] 的均值为代表,绘制5个等别尾矿库的尾矿水平运移距离.相应坝高为:15 m (五等库)、45 m (四等库)、85 m (三等库)、150 m (二等库)、250 m (一等库).根据式(45)绘制水平运移距离$S$变化曲线,如图3 所示. ...