矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础。能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史。变分法可以用于处理函数变量的问题。截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果。例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题。混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] 。混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了。
本文将应用变分原理中的混合变量的最小势能原理讨论矩形板在静水压力作用下的弯曲问题,并最终得到矩形板受静水压力的数值精确解。应用Matlab软件计算出矩形板挠度的精确值,应用ANSYS模拟软件得到矩形板挠度模拟值,并对两项数值进行对比分析,说明本文方法具有更好的准确性。
1 三边简支一边固定矩形板
1.1 挠曲线方程
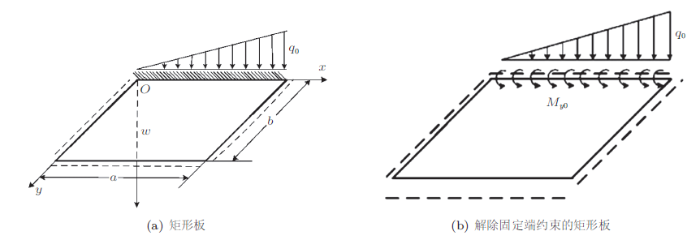
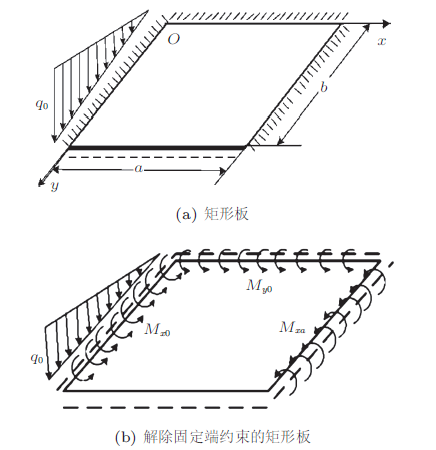
现考虑受静水压力的矩形板,边界条件如图1 (a)所示。图中$q_0$为三角形分布的均布载荷,$b$为矩形板沿$y$轴方向的长度,$a$为矩形板沿$x$轴方向的长度,$w$为挠度。以分布弯矩$M_{y0}$代替固定边的弯曲约束,创建如图1 (b)所示的变形后的等效图。
图1
(1) $\begin{eqnarray} \label{eq1} q=\frac{x}{a}q_{0} \end{eqnarray}$
(2) $\begin{eqnarray} \label{eq2} \overline{M}_{y0} =\sum\limits_{m=1,2}^{\infty} {C_{m} } \sin (\alpha_{m} x) \end{eqnarray}$
式中$C_{m}$为待定系数,$\alpha_{m}=m\pi/a$,同时假设板的弱容许挠度为
(3) $\begin{eqnarray} \label{eq3} &&w\left( {x,y} \right)=\sum\limits_{m=1,2}^{\infty} {\sum\limits_{n=1,2}^{\infty} {A_{mn} } } \sin (\alpha_{m} x)\sin(\beta_{n} y)\\&&\qquad 0\leqslant x\leqslant a,\ 0 \leqslant y\leqslant b \end{eqnarray}$
(4) $\begin{aligned}\Pi_{m_{\mathrm{P}}} &=\int_{0}^{a} \int_{0}^{b} \frac{D}{2}\left\{\left(\frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial y^{2}}\right)^{2}-\right.\\&\left.2(1-v)\left[\frac{\partial^{2} w}{\partial x^{2} \partial y^{2}}-\left(\frac{\partial^{2} w}{\partial x \partial y}\right)^{2}\right]\right\} \mathrm{d} x \mathrm{~d} y-\\& \int_{0}^{a} \int_{0}^{b} q w \mathrm{~d} x \mathrm{~d} y-\int_{0}^{a} \bar{M}_{y 0}\left(\frac{\partial w}{\partial y}\right)_{y=0} \mathrm{~d} x\end{aligned}$
式中$D={Eh^{3}}/[{12\left( {1-\nu^{2}}\right)}]$,为板的抗弯刚度,$E$为弹性模量,$\nu$为泊松比。
将式(1)和式(2)代入式(4)经过积分运算并且对$A_{mn}$取变分极值得
(5) $\begin{eqnarray} \label{eq5} &&A_{mn} =\frac{4q_{0} }{Dab}\frac{1}{K_{mn}^{2} }\frac{1}{\alpha_{m}\beta_{n} }\left( {-1} \right)^{m}\left[ {\left( {-1} \right)^{n}-1} \right]+\\&&\qquad \frac{2}{Db}\frac{\beta_{n} }{K_{mn}^{2} }C_{m} \end{eqnarray}$
式中$ K_{mn} =\alpha_{m}^{2} +\beta_{n}^{2} $。
(6) $\begin{eqnarray} \label{eq6} &&\hspace{-3mm}w\left( {x,y} \right)=\frac{4q_{0} }{Dab}\sum\limits_{m=1,2}^{\infty} {\sum\limits_{n=1,2}^{\infty} {(-1)^{m}} } \left[ {1-(-1)^{n}} \right]\cdot \\&&\hspace{-3mm}\qquad\frac{1}{\alpha_{m} \beta_{n} }\frac{1}{K_{mn}^{2} }\sin (\alpha _{m} x)\sin (\beta_{n} y)+ \\&&\hspace{-3mm}\qquad \frac{2}{Db}\sum\limits_{m=1,2}^{\infty} {\sum\limits_{n=1,2}^{\infty} {\frac{\beta_{n} }{K_{mn}^{2} }} } C_{m} \sin (\alpha_{m} x)\sin(\beta_{n}y) \end{eqnarray}$
在推导本边界条件挠曲线方程的过程中,式(6)是用混合变量最小势能原理导出的以正弦双重三角级数表示的弱容许挠度。而对于非齐次挠度和弯矩边界条件,正弦双重三角级数将会在边界上出现第二类间断点。为避免出现这种情况,并且能够加快级数收敛速度,需要将式(6)转换成为在边界上连续可微的挠度,而该挠度即为本次边界条件下的挠度表达式。应用文献[5 ]中附录式(A92)和式(A47)分别对式(6)各项进行转化,则得
(7) $\begin{eqnarray} &&\hspace{-4mm}w\left( {x,y} \right)=\frac{2q_{0} }{Da}\sum\limits_{m=1,2}^{\infty} {(-1)^{m+1}} \bigg\{ 1+\frac{1}{2\cosh(\alpha_{m}b/2)}\cdot \\[1mm]&&\hspace{-4mm}\quad\bigg[\alpha_{m} \lt(y-\frac{b}{2})\sinh \lt(y-\frac{b}{2}) -\\[1mm]&&\hspace{-4mm}\quad\left( {2+\frac{\alpha_{m} b}{2}\tanh \lt(\frac{1}{2}\alpha _{m} b)} \right)\cosh \lt[\alpha_{m} \lt(y-\frac{b}{2})]\bigg] \bigg\}\cdot \\[1mm]&&\hspace{-4mm}\quad \frac{1}{\alpha_{m}^{5} }\sin (\alpha_{m} x)+\frac{1}{2D}\sum\limits_{m=1,2}^{\infty} \big[ \alpha_{m} b\coth (\alpha _{m} b)-\\[1mm]&&\hspace{-4mm}\quad \alpha_{m} (b-y)\coth [\alpha_{m} (b-y)] \big] \frac{1}{\alpha _{m}^{2} \sinh (\alpha_{m} b)}\cdot\\[1mm]&&\hspace{-4mm}\quad \sinh [\alpha_{m} (b-y)]\sin (\alpha_{m} x)C_{m}, \\[1mm]&&\hspace{-3mm}\quad 0\leqslant x\leqslant a,\ \ 0\leqslant y\leqslant b \end{eqnarray}$
1.2 边界条件
固定端转角为0,故式(7)应符合式(8)的边界条件,其他边界条件已自动满足
(8) $\begin{eqnarray} \left( {\frac{\partial w}{\partial y}} \right)_{y=0} =0 \end{eqnarray}$
将方程式(7)代入式(8)中,经过运算整理可得执行方程
(9) $\begin{eqnarray} &&\hspace{-3mm}\frac{1}{2}\left( {\coth (\alpha_{m} b)-\frac{\alpha_{m} b}{\sinh^{2}(\alpha_{m} b)}} \right)\frac{1}{\alpha_{m} }C_{m}= \frac{q_{0} }{a}\left( {-1} \right)^{m}\cdot\\[1mm]&&\qquad\hspace{-3mm}\bigg( \tan\lt(\frac{1}{2}\alpha_{m} b)- \frac{1}{2}\alpha_{m} b\frac{1}{\cosh^{2}(\alpha_{m} b/2)} \bigg)\frac{1}{\alpha_{m}^{4} } \end{eqnarray}$
1.3 数值计算
取矩形板的各项参数:$a=b=1$ m,泊松比$\nu=0.3$,弹性模量 $E=2.0\times 10^{11}$ Pa,板的厚度$h=0.01$ m,静水压力$q_0=1$ MPa。其中含有未知项$C_{m}$。其次,应用Matlab软件编程计算,可求得具体挠度值。对计算程序循环50次,便可保障计算结果的收敛性。
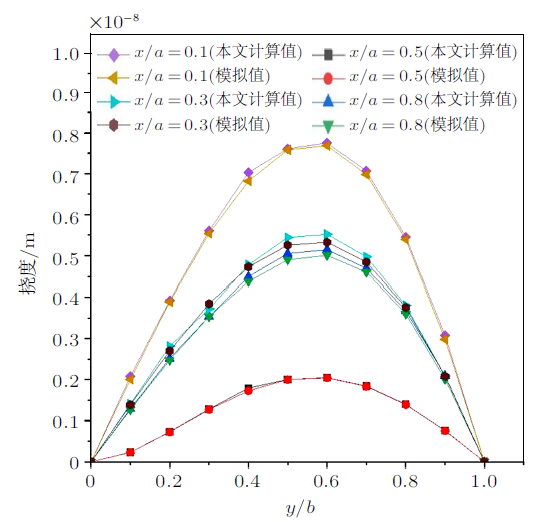
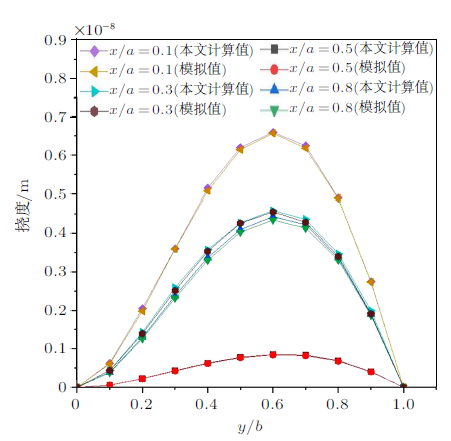
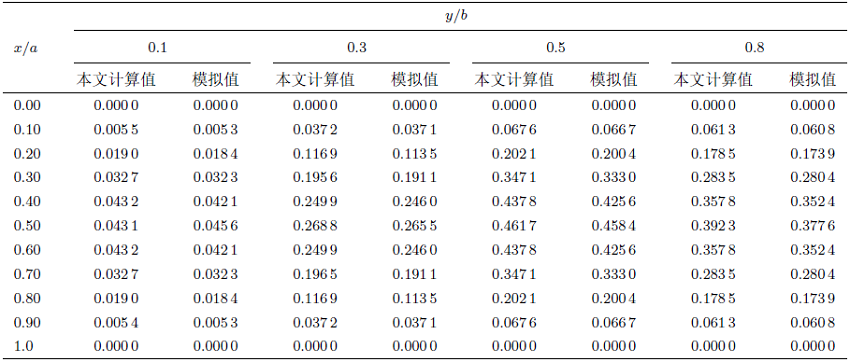
同时,应用模拟软件对本次边界条件下的矩形板进行建模分析,作为参考解与本文解进行对比。此种边界条件选用模型shell63单元,该单元具有弯曲能力和薄膜效应,并且忽略剪切变形,可以很好地应用于矩形板变形过程中的数值模拟。弯曲矩形板在$x/a =0.1$,$x/a =0.3$,$x/a =0.5$和$x/a =0.8$与$y/b =0.1$,$y/b =0.3$,$y/b =0.5$和$y/b =0.8$线上的模拟数值与本文计算数值两项数据绘制成图和表,如图2 与表1 所示。
图2
图2
$x/a=0.1$, $x/a=0.3$, $x/a=0.5$ 和 $x/a=0.8$处挠度分布曲线图
1.4 结果分析
图2 为矩形板沿$x$轴不同位置处的本文计算值和模拟值的挠度对比曲线图,可以直观看到,由于结构受三角形载荷作用,矩形板在静水压力作用下的挠度并非对称分布变化,且符合实际受力变化规律,计算结果更为贴近实际,这也间接说明混合变量 的最小势能原理解决矩形板受静水压力问题的适用性。
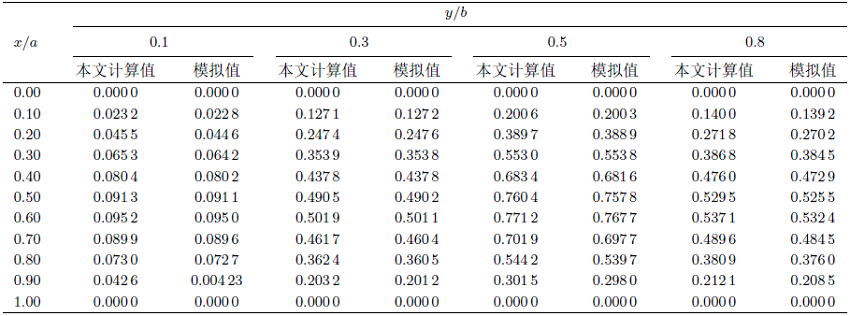
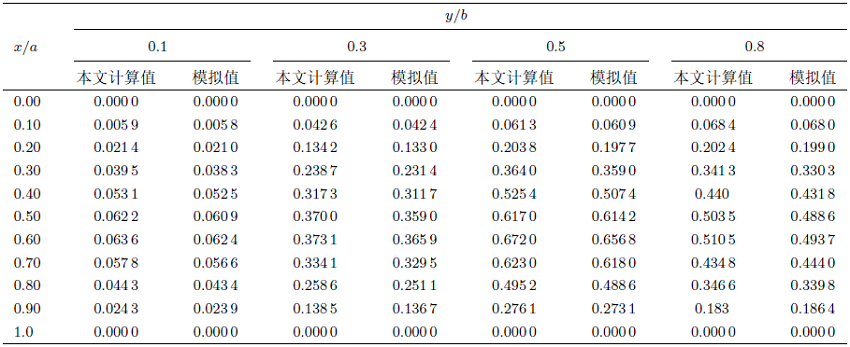
表1 给出了矩形板在$y/b =0.1$,$y/b =0.3$, $y/b =0.5$和$y/b=0.8$位置处沿$x$轴方向变化的挠度计算值和模拟参考值。通过对两项数值的对比分析,可以得到两者挠度的最大相对差值分别为:4.0%,3.8%,3.7%,本文研究方法计算的挠度值略大于有限元模拟的参考解,表明本方法可以更好地保证结构安全,反映结构在载荷作用下的变形规律,对矩形板弯曲解拥有更好的有效性和适用性,可以更精准地计算矩形板的挠度问题。
2 两邻边固定两邻边简支矩形板
2.1 挠曲线方程
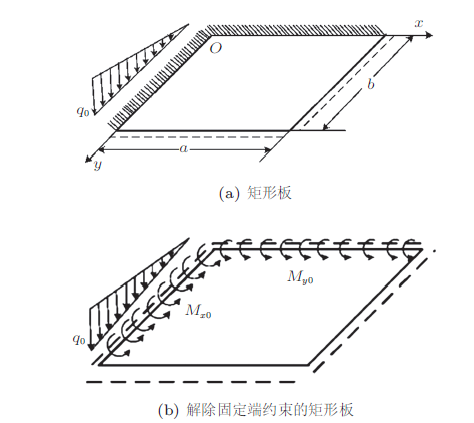
现考虑受静水压力的矩形板,边界条件如图3 (a)所示。以分布弯矩$M_{x0}$,$M_{y0}$代替固定边的弯曲约束,创建如图3 (b)所示的变形后的等效图。
图3
(10) $\begin{eqnarray} q=\frac{y}{b}q_{0} \end{eqnarray}$
(11) $\begin{eqnarray} &&\overline{M}_{x0} =\sum\limits_{n=1,2}^{\infty} {A_{n} } \sin (\beta_{n} y)\end{eqnarray}$
(12) $\begin{eqnarray} &&\overline{M}_{y0} =\sum\limits_{m=1,2}^{\infty} {C_{m} } \sin (\alpha_{m} x) \end{eqnarray}$
式中,$A_{n}$为待定系数。同时假设板的弱容许挠度为
(13) $\begin{eqnarray} &&w(x,y)=\sum\limits_{m=1,2}^{\infty} {\sum\limits_{n=1,2}^{\infty} {A_{mn} } } \sin (\alpha_{m} x)\sin(\beta_{n} y), \\&&\qquad 0\leqslant x\leqslant a,0\leqslant y\leqslant b \end{eqnarray}$
(14) $\begin{eqnarray} &&\varPi_{mp} =\int_0^a \int_0^b \Bigg\{ \left( {\frac{\partial ^{2}w}{\partial x^{2}}+\frac{\partial^{2}w}{\partial y^{2}}} \right)^{2}-2(1-v)\cdot \\&&\qquad \left[ {\frac{\partial^{2}w}{\partial x^{2}}\frac{\partial^{2}w}{\partial y^{2}}-\left( {\frac{\partial ^{2}w}{\partial x\partial y}} \right)^{2}} \right] \Bigg\} {\rm d}x{\rm d}y -\\&&\qquad \int_0^a \int_0^b qw{\rm d}x{\rm d}y -\int_0^b {\overline M_{x0} } \left( {\frac{\partial w}{\partial x}} \right)_{x=0} {\rm d}y -\\&&\qquad\int_0^a {\overline M _{y0} } \left( {\frac{\partial w}{\partial y}} \right)_{y=0} {\rm d}{x} \end{eqnarray}$
将式(10)$\sim$式(12)代入式(14)经过积分运算并且对$A_{mn}$取变分极值得
(15) $\begin{eqnarray} &&A_{mn} =\frac{4q_{0} }{Dab}\frac{1}{K_{mn}^{2} }\frac{1}{\alpha_{m} \beta _{n} }\left( {-1} \right)^{m}\left[ {1-\left( {-1} \right)^{n}} \right]+\\&&\qquad\frac{2}{Da}\frac{\alpha { }_{m}}{K_{mn}^{2} }A_{n} +\frac{2}{Db}\frac{\beta_{n} }{K_{mn}^{2} }C_{m} \end{eqnarray}$
(16) $\begin{eqnarray} &&w(x,y)=\frac{4q_{0} }{Dab}\sum\limits_{m=1,2}^{\infty} {\sum\limits_{n=1,2}^{\infty} {\left( {-1} \right)^{m}} } \left[ {\left( {-1} \right)^{n}-1} \right]\cdot\\&&\qquad\frac{1}{\alpha_{m} \beta_{n} }\frac{1}{K_{mn}^{2} }\sin (\alpha_{m} x)\sin(\beta_{n} y) +\\&&\qquad\frac{2}{Da}\sum\limits_{m=1,2}^{\infty} {\sum\limits_{n=1,2}^{\infty} {\frac{1}{K_{mn}^{2} }} } \frac{m\pi }{a}A_{n} \sin (\alpha_{m} x)\cdot\\&&\qquad\sin (\beta _{n} y) +\frac{2}{Db}\sum\limits_{m=1,2}^{\infty} {\sum\limits_{n=1,2}^{\infty} {\frac{1}{K_{mn}^{2} }} } \frac{n\pi }{b}C_{m}\cdot\\&&\qquad \sin (\alpha_{m} x)\sin (\beta _{n} y), \\&&\qquad 0\leqslant x\leqslant a,\ 0\leqslant y\leqslant b \end{eqnarray}$
同理,需要将式(16)转换成双曲函数和三角级数混合表示的基本解。应用文献[5 ]中附录式(A47)和式(A92)分别对式(16)各项进行转化,得
(17) $\begin{eqnarray} &&w(x,y)=-\frac{2q_{0}}{Da}\sum\limits_{m=1,2}^{\infty} \bigg[ \big(2+\alpha_{m} b\coth (\alpha_{m} b) \big)\cdot\\[1mm]&&\qquad\frac{1}{\sinh(\alpha _{m} b)} \sinh (\alpha_{m} y)- \frac{1}{\sinh (\alpha_{m} b)}\alpha_{m} y\cdot\\[1mm]&&\qquad\cosh (\alpha_{m} y) -\frac{2}{b}y \bigg]\frac{1}{\alpha_{m}^{5}}\sin (\alpha_{m}x) +\\[1mm]&&\qquad\frac{1}{2D}\sum\limits_{n=1,2}^{\infty} \big[ \beta_{n} a\coth (\beta _{n} a)-\\[1mm]&&\qquad \beta_{n} \left( {a-x} \right)\coth [\beta_{n} \left( {a-x} \right)] \big]\cdot\\[1mm]&&\qquad\frac{1}{\beta_{n}^{2} \sin (\beta_{n} a)}\sinh[\beta_{n} (a-x)]\sin (\beta_{n} y)(A_{n})+\\[1mm]&&\qquad\frac{1}{2D}\sum\limits_{m=1,2}^{\infty} \big[ \alpha_{m} b\coth\alpha_{m} b-\\[1mm]&&\qquad\alpha_{m} \left( {b-y} \right)\coth [\alpha_{m} \left( {b-y} \right)] \big]\cdot\\[1mm]&&\qquad \frac{1}{\alpha_{m}^{2} \sinh( \alpha_{m} b)}\sinh[\alpha_{m} \left( {b-y} \right)]\sin (\alpha_{m} x)C_{m}, \\[1mm]&&\qquad 0\leqslant x\leqslant a,\ 0\leqslant y\leqslant b \end{eqnarray}$
2.2 边界条件
固定端应满足转角为零,故式(17)应符合式(18)和式(19)的边界条件,其他边界条件已自动满足
(18) $\begin{eqnarray} &&\left( {\frac{\partial w}{\partial x}} \right)_{x=0} =0\end{eqnarray}$
(19) $\begin{eqnarray} &&\left( {\frac{\partial w}{\partial y}} \right)_{y=0} =0 \end{eqnarray}$
将方程式(17)代入式(18)和式(19)中,运算整理得执行方程
(20) $\begin{eqnarray} &&\frac{1}{2}\left( {\coth \bigg(\frac{1}{2}\beta_{n}\bigg) -\frac{\beta _{n} a}{2\cosh^{2}(\beta_{n} a)}} \right)\frac{1}{\beta_{n} }{A_{n} } +\\&&\qquad\frac{2}{b}\sum\limits_{m=1,2}^{\infty} {\frac{1}{K_{mn}^{2} }} \left( {\frac{m\pi }{a}} \right)\left( {\frac{n\pi }{b}} \right) {C_{m} } =\\&&\qquad\frac{1}{b}\left( {\tanh \lt(\frac{1}{2}\beta_{n} a)-\frac{\beta_{n} a}{2\cosh ^{2}(\beta_{n} a)}} \right)\frac{1}{\beta_{n}^{4} } \end{eqnarray}$
(21) $\begin{eqnarray} &&\frac{2}{a}\sum\limits_{m=1,2}^{\infty} {\frac{1}{K_{mn}^{2} }} \left( {\frac{m\pi }{a}} \right)\left( {\frac{n\pi }{b}} \right){A_{n} }+\\&&\qquad\frac{1}{2}\left( {\coth(\alpha_{m} b)-\frac{\alpha_{m} b}{\sinh ^{2}(\alpha_{m} b)}} \right)\frac{1}{\alpha_{m} }{C_{m} } =\\&&\qquad\frac{2q_{0} }{a}\bigg( \alpha_{m} b\coth(\alpha_{m} b)+\\&&\qquad \frac{1}{\sinh (\alpha_{m} b)}-\frac{2}{\alpha_{m} b} \bigg)\frac{1}{\alpha_{m}^{4} } \end{eqnarray}$
2.3 数值计算
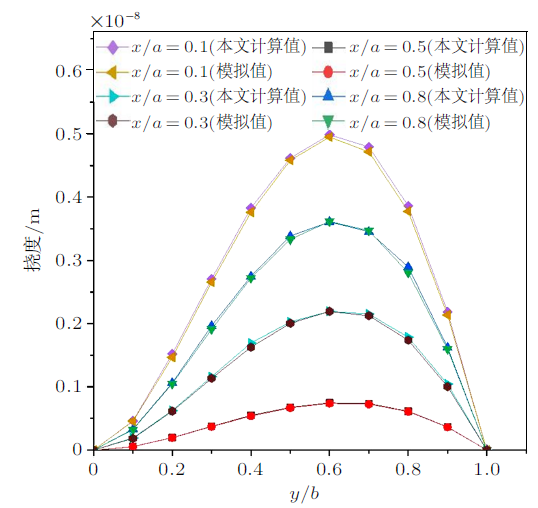
通过之前的公式推导,已经得到本边界条件的执行方程。且矩形板的计算参数与1.3相同。本节中所需要求解的未知数是$A_{n}$和$C_{m}$,对计算程序循环50次,运行结果不再变化,得到本边界条件下的挠度值。应用模拟软件对本次边界条件下的矩形板进行建模分析,单元类型采用Shell63,将弯曲矩形板在$x/a = 0.1$,$x/a = 0.3$,$x/a =0.5$ 和 $x/a = 0.8$ 与$y/b = 0.1$,$y/b = 0.3$,$y/b = 0.5$和$y/b = 0.8$线上的模拟数值与本文计算数值分别绘制成图和表,如图4 与表2 所示。
图4
图4
$x/a = 0.1$,$x/a = 0.3$,$x/a = 0.5$和$x/a = 0.8$处挠度分布曲线图
2.4 结果分析
图4 给出了矩形板沿$x$轴不同位置处的本文计算值和模拟值的挠度对比曲线图,可以直观看出,本文研究方法计算的挠度值略大于有限元模拟的参考解,表明本方法可以更好地保证结构安全,反映结构在载荷作用下的变形规律,对矩形板弯曲解具有更好的有效性和适用性,可以更精准地计算矩形板的挠度问题。由于受到载荷分布位置与边界条件不同的影响,矩形板的挠度曲线均沿坐标轴先增大后减小,且在$x/a=0.6$的位置达到了最大值。表明计算出的矩形板在静水压力作用下的挠度变化是符合 受力变化规律的。
表2 给出了矩形板在$y/b =0.1$,$y/b =0.3$, $y/b =0.5$和$y/b =0.8$位置处沿$x$轴方向变化的挠度公式计算值和模拟值。通过对两项数值的对比分析,可以得到两者挠度的最大相对差值分别为:3.5%、3.4%、3.0%,本文研究方法计算的挠度值略大于有限元模拟的参考解,表明本方法可以更好地保证结构 安全,反映结构在载荷作用下的变形规律,使矩形板挠度问题的计算更为精确。
3 三边固定一边简支矩形板
3.1 挠曲线方程
现考虑受静水压力的矩形板,边界条件如图5 (a)所示。以分布弯矩$M_{x0}$,$M_{y0}$,$M_{xa}$代替固定边的弯曲约束,创建如图5 (b)所示的变形后的等效图。
图5
(22) $\begin{eqnarray} q=\frac{y}{b}q_{0} \end{eqnarray}$
(23) $\begin{eqnarray} &&\overline M_{x0} =\overline M_{xa} =\sum\limits_{n=1,2}^{\infty} {A_{n} } \sin (\beta_{n} y)\end{eqnarray}$
(24) $\begin{eqnarray} &&\overline M_{y0} =\sum\limits_{m=1,2}^{\infty} {C_{m} } \sin (\alpha_{m} x) \end{eqnarray}$
(25) $\begin{eqnarray} &&w\left( {x,y} \right)==\sum\limits_{m=1,2}^{\infty} {\sum\limits_{n=1,2}^{\infty} {A_{mn} \sin (\alpha_{m} x)\sin (\beta_{n} y)} }, \\&&\qquad0\leqslant x\leqslant a,\ 0\leqslant y\leqslant b \end{eqnarray}$
(26) $\ni\begin{eqnarray} &&\varPi_{m{\rm p}} =\int_0^a \int_0^b \frac{D}{2} \bigg\{ \left( {\frac{\partial^{2}w}{\partial x^{2}}+\frac{\partial^{2}w}{\partial y^{2}}} \right)^{2}-2\left( {1-\nu} \right)\cdot\\&&\qquad\left[ {\frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial^{2}w}{\partial y^{2}}-\left( {\frac{\partial^{2}w}{\partial x\partial y}} \right)^{2}} \right] \bigg\}{\rm d}x{\rm d}y-\\&&\qquad\int_0^a \int_0^b qw{\rm d}{x}{\rm d}{y} -\int_0^b {\overline M_{x0} } \left( {\frac{\partial w}{\partial x}} \right)_{x=0} {\rm d}{y} +\\&&\qquad \int_0^b {\overline M _{xa} } \left( {\frac{\partial w}{\partial x}} \right)_{x=a} {\rm d}{y} -\\&&\qquad\int_0^a {\overline M_{y0} } \left( {\frac{\partial w}{\partial y}} \right)_{y=0} {\rm d}{x} \end{eqnarray}$
将式(22)$\sim$式(24)代入式(26)经过积分运算并且对$A_{mn}$取变分极值得
(27) $\begin{eqnarray} &&\hspace{-5mm}A_{mn} =\frac{\mbox{4}q_{0} }{Dab}\frac{1}{K_{mn}^{2} }\frac{1}{\alpha_{m} \beta_{n} }(-1)^{m}\left[ {1-(-1)^{n}} \right]+\\&&\hspace{-5mm}\qquad \frac{2}{Da}\frac{\alpha _{m} }{K_{mn}^{2} }\left[ {1-(-1)^{m}} \right]A_{n} +\frac{2}{Db}\frac{\beta_{n} }{K_{mn}^{2} }C_{m} \end{eqnarray}$
(28) $\begin{eqnarray} &&w\left( {x,y} \right)=\frac{4q_{0} }{Dab}\sum\limits_{m=1,2}^{\infty} {\sum\limits_{n=1,2}^{\infty} {\left( {-1} \right)^{m}} } \left[ {(-1)^{n}-1} \right]\cdot \\&&\qquad\frac{1}{\alpha_{m} \beta_{n} }\frac{1}{K_{mn}^{2} }\sin (\alpha _{m} x)\sin (\beta_{n} y) +\\&&\qquad\frac{2}{Da}\sum\limits_{m=1,2}^{\infty} {\sum\limits_{n=1,2}^{\infty} {\frac{1}{K_{mn}^{2} }} } \frac{m\pi }{a}\left[ {1-(-1)^{m}} \right]\cdot \\&&\qquad A_{n} \sin (\alpha_{m} x)\sin (\beta_{n} y) +\\&&\qquad\frac{2}{Db}\sum\limits_{m=1,2}^{\infty} {\sum\limits_{n=1,2}^{\infty} {\frac{1}{K_{mn}^{2} }} } \frac{n\pi }{b}C_{m} \sin (\alpha_{m} x)\sin (\beta _{n} y), \\&&\qquad0\leqslant x\leqslant a,\ 0\leqslant y\leqslant b \end{eqnarray}$
同理,需要将式(28)转换成双曲函数和三角级数混合表示的基本解。应用文献[5 ]中附录式(A47)和式(A92)分别对式(28)各项进行转化,可得
(29) $\begin{eqnarray} &&\hspace{-3mm}w\left( {x,y} \right)=-\frac{2q_{0} }{Db}\sum\limits_{m=1,2}^{\infty} \bigg[ \left( 2+\alpha_{m} b\coth (\alpha_{m} b) \right)\cdot\\&&\hspace{-3mm}\qquad\frac{1}{\sinh \alpha _{m} }\sin (\alpha_{m} y)- \frac{1}{\sinh (\alpha_{m} b)}\alpha_{m} y\cos (\alpha_{m} y)-\\&&\hspace{-3mm}\qquad\frac{2}{b}y \bigg]\frac{1}{\alpha_{m}^{5}}\sin (\alpha_{m} x) \cdot \left( {a-x} \right)\sin (\beta_{n} y){A_{n} }+\\&&\hspace{-3mm}\qquad\frac{1}{2D}\sum\limits_{n=1,2}^{\infty} {\left( {\beta_{n} a\coth (\beta_{n} a)-\beta_{n} x\coth (\beta_{n} x)} \right)}\cdot\\&&\hspace{-3mm}\qquad \frac{1}{\beta _{n}^{2} \sinh (\beta_{n} a)} \sinh (\beta_{n} x)\sin (\beta_{n} y){A_{n} }+\frac{1}{2D}\cdot \\&&\hspace{-3mm}\qquad\sum\limits_{n=1,2}^{\infty}\big[ \alpha_{m} b\coth (\alpha_{m} b)-\alpha_{m} \left( {b-y} \right) \cdot\\&&\hspace{-3mm}\qquad \coth [\alpha_{m} (b-y)]\big] \frac{1}{\alpha_{m}^{2} \sinh (\alpha_{m} b)}\cdot\\&&\hspace{-3mm}\qquad\sinh [\alpha_{m} \left( {b-y} \right)] \sin (\alpha_{m} x)C_{m}, \\&&\hspace{-3mm}\qquad 0\leqslant x\leqslant a,0\leqslant y\leqslant b \end{eqnarray}$
3.2 边界条件
固定端应满足转角为零,故式(29)应符合式(30)和式(31)的边界条件,其他边界条件已自动满足
(30) $\begin{eqnarray} &&\left( {\frac{\partial w}{\partial x}} \right)_{x=0} =\left( {\frac{\partial w}{\partial x}} \right)_{x=a} =0 \end{eqnarray}$
(31) $\begin{eqnarray} &&\left( {\frac{\partial w}{\partial x}} \right)_{y=0} =0 \end{eqnarray}$
把方程式(29)代入式(30)和式(31)中,经过运算整理得执行方程。
(32) $\begin{eqnarray} &&\frac{1}{2}\left( {\coth (\beta_{n} a)-\frac{\beta_{n} a}{\sinh^{2}(\beta_{n} a)}} \right)\frac{1}{\beta_{n} }{A_{n} }-\\[1mm]&&\qquad\frac{1}{2}\left( {\beta_{n} a\coth (\beta_{n} a)-1} \right){A_{n} } +\frac{2}{b}\sum\limits_{m=1,2}^{\infty} {\frac{1}{K_{mn}^{2} }}\cdot\\[1mm]&&\qquad \left( {\frac{m\pi }{a}} \right)\left( {\frac{n\pi }{b}} \right){C_{m} }=\frac{q_{0} }{b}\left( {-1} \right)^{n}\cdot\\[1mm]&&\qquad\bigg( \tanh \frac{1}{2}(\beta_{n} a)- \frac{\beta_{n} a}{2\cosh^{2}(\beta_{n} a)} \bigg)\frac{1}{\beta _{n}^{4} }\\[1mm] \end{eqnarray}$
(33) $\begin{eqnarray} &&\frac{2}{a}\sum\limits_{m=1,2}^{\infty} {\frac{1}{K_{mn}^{2} }} \left( {\frac{m\pi }{a}} \right)\left( {\frac{n\pi }{b}} \right){A_{n} }-\\[1mm]&&\qquad\frac{2}{a}\sum\limits_{m=1,2}^{\infty} {\frac{1}{K_{mn}^{2} }} \left( {-1} \right)^{m}\left( {\frac{m\pi }{a}} \right)\left( {\frac{n\pi }{b}} \right){A_{n} } +\\[1mm]&&\qquad\frac{1}{2}\left( {\mbox{coth}(\alpha_{m} b)-\frac{\alpha_{m} b}{\sinh ^{2}(\alpha_{m} b)}} \right)\frac{1}{\alpha_{m} }C_{m}=\\[1mm]&&\qquad\frac{2q_{0} }{a}\bigg( \alpha_{m} b\coth (\alpha_{m} b)\frac{1}{\sinh (\alpha_{m} b)}+\\[1mm]&&\qquad \frac{1}{\sinh (\alpha_{m} b)}-\frac{1}{\alpha_{m} b} \bigg)\frac{1}{\alpha_{m}^{4} } \end{eqnarray}$
3.3 数值计算
通过之前的公式推导,已经得到本边界条件的执行方程。且矩形板的计算参数与1.3相同。本节中所需要求解的未知数是$A_{n}$和$C_{m}$,同理为了保障计算数值的收敛性,对计算程序循环50次,得到本边界条件下的挠度值,并通过模拟软件模拟分析,将模拟结果作为参考值。将弯曲矩形板在$x/a =0.1$,$x/a =0.3$,$x/a =0.5$和$x/a =0.8$与$y/b =0.1$,$y/b =0.3$,$y/b =0.5$和$y/b =0.8$线上的模拟数值与本文计算数值两项数据分别绘制成图和表,如图6 与表3 所示。
图6
图6
$x/a =0.1$,$x/a=0.3$,$x/a=0.5$和$x/a =0.8$处挠度分布曲线图
3.4 结果分析
图6 给出了矩形板沿$y$轴不同位置处的本文计算值和模拟值的挠度对比曲线图,可以直观看出,由于受到载荷分布位置与边界条件不同的影响,矩形板的挠度曲线都沿坐标轴先增大后减小,且在$x/a=$0.6的位置达到了最大值。表明计算出的矩形板在静水压力作用下的挠度变化符合受力变化规律。
表3 给出了矩形板在$y/b =0.1$,$y/b =0.3$, $y/b =0.5$和$y/b =0.8$位置处沿$x$轴方向变化的挠度公式计算值和模拟值。通过对两项数值的对比分析,可以得到两者挠度的最大相对差值分别为:4.2%、3.9%、3.2%,本文研究方法计算的挠度值略 大于有限元模拟的参考解,表明本方法可以更好地保证结构安全,并且对求解矩形板弯曲解拥有更好的有效性和适用性。
4 结论
本文依据混合变量的最小势能原理推导出了三边简支一边固定、两邻边固定两邻边简支、三边固定一边简支三种不同边界条件的弯曲矩形板在静水压力作用下的边界应力函数的表达式和封闭解析解,数值计算软件求得的数值解与模拟软件的模拟值进行归纳分析,表明本文方法的正确性,说明了本文研究方法可以使矩形板的弯曲问题的求解简单化和精确化。
参考文献
View Option
[1]
卢圣治 . 变分法初步
大学物理 , 1988 (4 ): 38 -42
[本文引用: 1]
Lu Shengzhi . Preliminary variational method
University Physics 1988 (4 ): 38 -42
[本文引用: 1]
[2]
刘国钰 . 变分原理在物理学理论研究中的重要作用
电大理工 , 2013 (2 ): 48 -50, 81
[本文引用: 1]
Liu Guoyu . Important role of variational principle in theoretical research of physics
Science and Technology of RTVU 2013 (2 ): 48 -50, 81
[本文引用: 1]
[3]
王根会 , 樊江 , 操俊林 等 . 新型组合箱梁竖向弯曲力学行为的研究
铁道工程学报 , 2019 , 36 (9 ): 23 -30, 48
[本文引用: 1]
Wang Genhui Fan Jiang Cao Junlin , et al . Research on the vertical bending mechanical behaviors of new composite box girder
Journal of Railway Engineering 2019 , 36 (9 ): 23 -30, 48 (in Chinese)
[本文引用: 1]
[4]
曾祥勇 , 邓安福 , 丁济新 . 弹性半空间体上矩形筏板的变分分析方法
地下空间 , 2001 (1 ): 67 -75
[本文引用: 1]
Zeng Xiangyong Deng Anfu Ding Jixin . Variational analysis method of rectangular raft on elastic half space
Underground Space 2001 (1 ): 67 -75
[本文引用: 1]
[5]
付宝连 . 弹性力学混合变量的变分原理及其应用 . 北京 : 国防工业出版社 , 2010
[本文引用: 4]
Fu Baolian . Variational Principle of Mixed Variables in Elasticity and Its Application . Beijing : National Defense Industry Press , 2010
[本文引用: 4]
[6]
鲍四元 , 沈峰 . 各向异性矩形板和环扇形板横向自由振动的一种通用解法
固体力学学报 , 2019 , 40 (6 ): 560 -570
[本文引用: 1]
Bao Siyuan Shen Feng . A General method for transverse free vibration of anisotropic rectangular plates and ring sector plates
Chinese Journal of Solid Mechanics 2019 , 40 (6 ): 560 -570
[本文引用: 1]
[7]
张紫祥 . 任意位置集中载荷作用下复合材料圆弧浅拱的非线性面内弹性稳定
第28届全国结构工程学术会议, 南昌 , 2019
[本文引用: 1]
Zhang Zixiang . Nonlinear in-plane elastic stability of composite circular arc shallow arch under concentrated load at any position
28 National Conference on Structural Engineering, Nanchang , 2019 (in Chinese)
[本文引用: 1]
[8]
孙加平 , 魏星 , 宋保保 . 基于最小势能原理的三维边坡稳定矢量和法
长江科学院院报 , 2020 , 37 (11 ): 102106
Sun Jiaping Wei Xing Song Baobao . Three-dimensional slope stability vector sum method based on minimum potential energy principle
Journal of Yangtze River Scientific Research Institute 2020 , 37 (11 ): 102106 (in Chinese)
[9]
Tan Junyu . Remarks of some problems for rectangular thin plates with free edges on elastic foundations
Applied Mathematics and Mechanics (English Edition )1991 , 12 (4 ): 415 -420
DOI
URL
[本文引用: 1]
[10]
István E Attila B . Saint--Venant torsion of cylindrical orthotropic elliptical cross section
Mechanics Research Communications 2019 , 99 : 42 -46
DOI
URL
[本文引用: 1]
[11]
王轶 . Hoek-Brown 准则最小势能法的路堤边坡安全系数计算研究
《工业建筑》2018 年全国学术年会, 北京 , 2018
[本文引用: 1]
[12]
Kanno Y Ohsaki M . Minimum principle of complementary energy for nonlinear elastic cable networks with geometrical nonlinearities
Journal of Optimization Theory and Applications 2005 , 126 (3 ): 617 -641
DOI
URL
[本文引用: 1]
变分法初步
1
1988
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
变分法初步
1
1988
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
变分原理在物理学理论研究中的重要作用
1
2013
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
变分原理在物理学理论研究中的重要作用
1
2013
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
新型组合箱梁竖向弯曲力学行为的研究
1
2019
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
新型组合箱梁竖向弯曲力学行为的研究
1
2019
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
弹性半空间体上矩形筏板的变分分析方法
1
2001
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
弹性半空间体上矩形筏板的变分分析方法
1
2001
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
4
2010
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
... 在推导本边界条件挠曲线方程的过程中,式(6)是用混合变量最小势能原理导出的以正弦双重三角级数表示的弱容许挠度.而对于非齐次挠度和弯矩边界条件,正弦双重三角级数将会在边界上出现第二类间断点.为避免出现这种情况,并且能够加快级数收敛速度,需要将式(6)转换成为在边界上连续可微的挠度,而该挠度即为本次边界条件下的挠度表达式.应用文献[5 ]中附录式(A92)和式(A47)分别对式(6)各项进行转化,则得 ...
... 同理,需要将式(16)转换成双曲函数和三角级数混合表示的基本解.应用文献[5 ]中附录式(A47)和式(A92)分别对式(16)各项进行转化,得 ...
... 同理,需要将式(28)转换成双曲函数和三角级数混合表示的基本解.应用文献[5 ]中附录式(A47)和式(A92)分别对式(28)各项进行转化,可得 ...
4
2010
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
... 在推导本边界条件挠曲线方程的过程中,式(6)是用混合变量最小势能原理导出的以正弦双重三角级数表示的弱容许挠度.而对于非齐次挠度和弯矩边界条件,正弦双重三角级数将会在边界上出现第二类间断点.为避免出现这种情况,并且能够加快级数收敛速度,需要将式(6)转换成为在边界上连续可微的挠度,而该挠度即为本次边界条件下的挠度表达式.应用文献[5 ]中附录式(A92)和式(A47)分别对式(6)各项进行转化,则得 ...
... 同理,需要将式(16)转换成双曲函数和三角级数混合表示的基本解.应用文献[5 ]中附录式(A47)和式(A92)分别对式(16)各项进行转化,得 ...
... 同理,需要将式(28)转换成双曲函数和三角级数混合表示的基本解.应用文献[5 ]中附录式(A47)和式(A92)分别对式(28)各项进行转化,可得 ...
各向异性矩形板和环扇形板横向自由振动的一种通用解法
1
2019
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
各向异性矩形板和环扇形板横向自由振动的一种通用解法
1
2019
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
任意位置集中载荷作用下复合材料圆弧浅拱的非线性面内弹性稳定
1
2019
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
任意位置集中载荷作用下复合材料圆弧浅拱的非线性面内弹性稳定
1
2019
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
基于最小势能原理的三维边坡稳定矢量和法
0
2020
基于最小势能原理的三维边坡稳定矢量和法
0
2020
Remarks of some problems for rectangular thin plates with free edges on elastic foundations
1
1991
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
Saint--Venant torsion of cylindrical orthotropic elliptical cross section
1
2019
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
Hoek-Brown 准则最小势能法的路堤边坡安全系数计算研究
1
2018
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...
Minimum principle of complementary energy for nonlinear elastic cable networks with geometrical nonlinearities
1
2005
... 矩形板作为结构基本构件之一,我们可以把矩形板理论分析方法归纳分为精确解法和近似解法,且这两类方法均以能量原理为基础.能量法又称为变分法,可以追溯到17世纪末,有着悠久的历史.变分法可以用于处理函数变量的问题.截止到目前,国内外学者普遍非常重视变分原理[1 -2 ] 的研究,而且已经有了丰硕的成果.例如:王根会等[3 ] 基于能量变分法推导了新型组合箱梁的总势能式与微分控制方程,为新型组合箱梁的应用推广提供了理论和技术支持;曾祥勇等[4 ] 以能量变分法的最小势能原理为基础分析了矩形筏板的受弯问题.混合变量的极 值变分原理[5 -6 ] 包含混合变量的最小势能原理[7 -9 ] 与混合变量的最小余能原理[10 ] .混合变量的极值变分原理,其容许位移与容许内力分别被弱容许位移与弱容许内力所代替,与传统理论[11 -12 ] 相比增强了等价方程,而且需要预先满足的条件减弱了. ...