层状弹性体系力学是多层柔性路面、机场道面以及多层地基设计与计算的理论基础。该理论及在其基础上所编制的各种实用程序在世界各国的上述工程结构的科学研究和设计与计算中得到了广泛的应用。

层状弹性体系力学是弹性力学的一个分支。层状弹性体系力学将所研究的物体看作是自上而下由若干弹性层和半无限弹性体组成的弹性体系。

尽管层状弹性体系力学属于弹性力学的范畴,但与传统的弹性力学相比,层状弹性体系力学有很大的不同。传统的弹性力学只能解决半无限弹性体的力学分析和计算问题,而层状弹性体系力学可以解决半无限层状弹性体系的力学分析和计算问题。在层状弹性体系力学中,经常采用汉克尔(Hankel)积分变换公式并频繁使用各种特殊函数(伽马(gamma)函数、贝塔(beta)函数、普西(psi)函数、椭圆积分、超几何函数、贝塞尔(Bessel)函数、勒让德(Legendre)函数、拉姆达(lambda)函数)的计算公式,而这两种计算公式在传统的弹性力学的力学分析与计算中很少出现或几乎不出现。因此层状弹性体系力学大大丰富了弹性力学的理论宝库。

目前在我国,层状弹性体系力学在交通工程界已得到广泛的应用,而在力学界则鲜为人知。本文是迄今国内第一次以论文的形式全面、系统地向国内广大读者宣传、介绍层状弹性体系力学的发展历史、基础理论、计算公式和计算方法及其在科学研究和工程设计中的应用。尽管层状弹性体系力学诞生已经几十年了,文中的内容对于国内很多读者来说,仍然是十分新鲜并具有理论价值和实用价值的知识,值得一读。

层状弹性体系力学是在半无限弹性体力学的基础上发展起来的。1885年,Boussinesq对半无限弹性体表面在单个垂直集中力作用下的应力和位移作出了理论解,它在近代土力学中获得了广泛的应用。1882 年,Cerruti对半无限弹性体表面在单个水平集中力作用下的应力和位移作出了理论解。

由于数学和弹性力学的发展,到20世纪40$\sim$60年代,层状弹性体系力学取得了长足的进步。1945年,Burmister^[1]利用Love位移函数得到了在轴对称垂直载荷作用下双层和多层弹性体系应力和位移的理论解。1962年,Schiffman^[2] 又将其进一步推广到多层弹性体系非轴对称问题的求解。

20世纪60$\sim$70年代,电子计算机及计算方法发展很快,而工程实际也要求解决多层(层数$N>3$)弹性体系的力学计算,于是多层弹性体系力学计算程序在各国学者的努力下应运而生。

1973 年,De Jong等^[3]合作编制成功BISAR (bitumen structures analysis in roads)计算机程序,该程序可以计算在多圆均布复合载荷(包括垂直、单向水平载荷)作用下$N$层弹性连续—半结合体系内任一点的应力和位移分量、主应力和主应变分量以及主方向等。

除此之外,世界各国还有不少计算$N$层弹性体系应力和位移分量的计算机程序,但迄今为止世界上公认比较有名、实用且影响比较深远的仍然是BISAR程序。

改革开放以来,随着交通事业的发展,高等级公路和城市道路沥青路面的大量设计与修建,我国迫切需要解决多层弹性体系的力学计算问题。但国外在这一方面对我国搞专利封锁,著名的BISAR程序专利费高达100万美元。

为了打破国外的专利封锁,中国学者们决心攻克这一国内难题。1980年笔者编制成功了在圆形均布垂直载荷作用下$N$层弹性连续体系的力学计算程序, 并从此开始将笔者本人编写的$N$层弹性体系力学计算程序统称为NESCP ($N$-layer elastic system computer program)程序^[4]。1981 年笔者又编制成功了在双圆均布复合载荷(垂直和单向水平载荷)作用下$N$层弹性连续体系的力学计算程序^[5]。在此基础上笔者经过数年努力,于1984年编制了功能更全面的多层弹性体系力学计算程序。该程序的功能已达 到BISAR程序的功能^[6-9]。1990 年,由笔者完成的“层状弹性体系应力与位移的一般分析与计算”课题获陕西省科技进步一等奖。

除了笔者之外,我国还有不少学者按照不同思路编制了若干多层弹性体系力学计算程序,较有影响的有朱照宏的“高阶矩阵代数法”程序^[10],郭文复的“分层求逆子阵的传递矩阵法”程序^[11],郭大智的“系数递推法”程序^[12]以 及吴晋伟的“反力递推法”程序^[13]等。

应当指出,由于国外技术封锁,我国多层弹性体系力学分析与计算的研究工作,基本上是在自力更生的基础上进行的,但这也促使我们的研究在很多方面具有中国特色。

由多层弹性体系力学计算可知,如何从线性代数方程组快速地求算出积分常数,是保证快速计算出应力与位移分量的关键。在这一方面,中外的学者们提出了不同的方法,一种是笔者提出的“递推回代法”,另一种是“传递矩阵法” (由于保密,国外文献中 从不介绍该计算方法的具体细节)。计算表明,“递推回代法”的计算时间少,不会出现“病态矩阵”,对层间完全连续、层间完全光滑和层间半结合时积分常数的求解问题都能解决,比“传递矩阵法” (该方法不能解决层间完全光滑时积分常数的求解问题) 明显优越。

积分计算公式是多层弹性体系力学计算的另一个关键计算公式。由于保密,国外文献中从不介绍积分计算公式的内容。笔者在前人工作的基础上,通过数学推导和误差分析,得到了论文中所述的积分计算公式并成功地应用于多层弹性体系的力学计算。

由于本文篇幅有限,有关内容的详细介绍,请参看参考文献[14]。

以上仅对层状弹性体系力学的发展历史作了简单的回顾,下文将进一步介绍$N$层弹性体系的力学分析与计算。

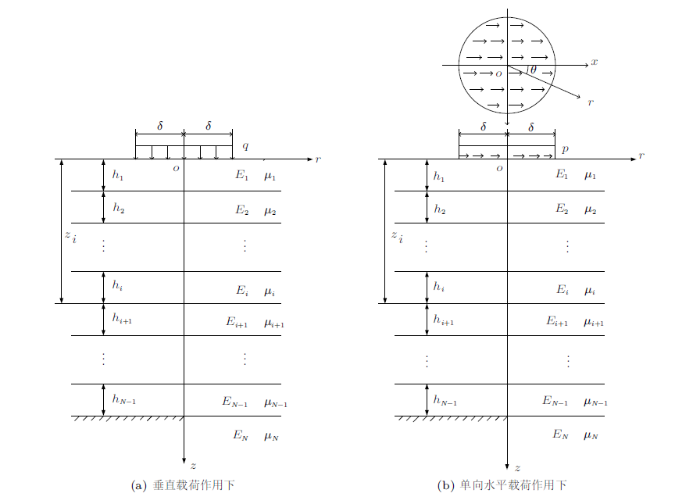
层状弹性体系力学包含了丰富的内容,由于篇幅有限,本文只着重介绍在工程实践中应用最广泛的在圆形均布垂直载荷或单向水平载荷作用下$N$层弹性体系的力学分析与计算并在介绍过程中对NESCP程序和BISAR程序的力学计算公式和计算方法进行比较。所谓$N$层弹性体系通常指自上而下由$N-1$层有限厚的水平弹性层和最下层半无限弹性体组成的体系。当$N=$1时,层状弹性体系即变为半无限弹性体。$N$层弹性体系在单圆均布垂直载荷或单向水平载荷作用下的力学计算简图如图1 所示。图中$q$和$p$分别为垂直载荷和水平载荷集度,$\delta$为载荷圆半径,$h_{i}$,$E_{i} $和$\mu_{i} $分别为弹性体系各层的厚度、弹性模量和泊松比。

为了进行层状弹性体系的力学分析,在层状弹性体系力学中关于层状弹性体系,引入如下几个基本假定：

(1)各层是连续的、完全弹性的、均匀的和各向同性的理想弹性体;

(2)最下层半无限弹性体在水平方向和垂直向下方向均为无限大,其上各层垂直方向具有有限的厚度,水平方向为无限大;

(3)各层水平无限远处和最下层无限深处,应力和位移分量为零;

(4)层间结合状况可以是完全连续的,或者是完全光滑的,或者是介于二者之间的半结合状况,但层间不出现脱空现象;

(5)体系受力后位移和变形是微小的,在进行力学分析时体力可忽略不计。

采用位移函数法和汉克尔积分变换的公式^[15]求解柱坐标系中弹性力学三维问题的基本方程,即可得到$N$层弹性体系在单圆均布垂直载荷或单向水平载荷作用下应力和位移分量的表达式：

当载荷为垂直载荷时

其中

\begin{eqnarray*} &&U_{1i} =q\int_0^\infty \dfrac{{\rm J}_{1} \bigg(\dfrac{r}{\delta }x\bigg){\rm J}_{1} (x)}{\dfrac{r}{\delta }x}\cdot\\[1mm]&&\qquad\bigg\{\bigg[C_{i} +\bigg(1+\dfrac{z}{\delta }x\bigg)A_{i} \bigg]{\rm e}^{\frac{z}{\delta }x}-\\[1mm]&&\qquad\bigg[D_{i} -\bigg(1-\dfrac{z}{\delta }x\bigg)B_{i} \bigg]{\rm e}^{-\frac{z}{\delta }x}\bigg\}{\rm d}x \end{eqnarray*}

当载荷为单向水平载荷时

其中

$\begin{eqnarray*} \begin{array}{l} U_{2i} =p\int_0^\infty \dfrac{{\rm J}_{2} \bigg(\dfrac{r}{\delta }x\bigg){\rm J}_{1} (x)}{x}\cdot\\[4mm]\qquad\bigg\{\bigg[C_{i} +\bigg(1+\dfrac{z}{\delta }x\bigg)A_{i} +2F_{i} \bigg]{\rm e}^{\frac{z}{\delta }x}-\\[4mm]\qquad\bigg[D_{i} -(1-\dfrac{z}{\delta }x)B_{i} -2I_{i} \bigg]{\rm e}^{-\frac{z}{\delta }x}\bigg\}{\rm d}x \\[3mm] V_{0i} =p\int_0^\infty \dfrac{{\rm J}_{0} \bigg(\dfrac{r}{\delta }x\bigg){\rm J}_{1} (x)}{x}\cdot\\[4mm]\qquad\bigg\{\bigg[C_{i} +\bigg(1+\dfrac{z}{\delta }x\bigg)A_{i} -2F_{i} \bigg]{\rm e}^{\frac{z}{\delta }x}-\\[4mm]\qquad\bigg[D_{i} -\bigg(1-\dfrac{z}{\delta }x\bigg)B_{i} +2I_{i} \bigg]{\rm e}^{-\frac{z}{\delta }x}\bigg\}{\rm d}x \\[3mm] T_{2i} =p\int_0^\infty {\rm J}_{2} \bigg(\dfrac{r}{\delta }x\bigg){\rm J}_{1} (x)\cdot\\[4mm]\qquad\bigg\{\bigg[C_{i} +\bigg(2\mu _{i} +\dfrac{z}{\delta }x\bigg)A_{i} +F_{i} \bigg]{\rm e}^{\frac{z}{\delta }x}+\\[4mm]\qquad\bigg[D_{i} -\bigg(2\mu _{i} -\dfrac{z}{\delta }x\bigg)B_{i} -I_{i} \bigg]{\rm e}^{-\frac{z}{\delta }x}\bigg\}{\rm d}x \\[3mm] S_{0i} =p\int_0^\infty{\rm J}_{0} \bigg(\dfrac{r}{\delta }x\bigg){\rm J}_{1} (x)\cdot\\[4mm]\qquad\bigg\{\bigg[C_{i} +\bigg(2\mu _{i} +\dfrac{z}{\delta }x\bigg)A_{i} -F_{i} \bigg]{\rm e}^{\frac{z}{\delta }x}+\\[4mm]\qquad\bigg[D_{i} -\bigg(2\mu _{i} -\dfrac{z}{\delta }x\bigg)B_{i} +I_{i} \bigg]{\rm e}^{-\frac{z}{\delta }x}\bigg\}{\rm d}x \\ \end{array} \end{eqnarray*}$

以上各式中,${\rm J}_{0} (x)$,${\rm J}_{1} (x)$和${\rm J}_{2} (x)$分别为零阶、一阶和二阶第一类贝塞尔函数,下标$i$表示各力学分量计算点所在的层数;$A_{i}$,$B_{i}$,$C_{i}$,$D_{i}$,$F_{i}$,$I_{i}$为积分常数,实际为积分变量$x$的函数。如下所述,它们将根据具体力学问题的定解条件来确定,其他各变量解释详见参考文献[14],下同。

2.3.1 NESCP程序

当载荷为垂直载荷时

(1) 表面应力边界条件($z=0$)

(2) 层间结合条件($z=z_{i} $)

此外,定解条件还有：当$z\to \infty $时,所有应力和位移分量均应趋于零,因此必有$A_{N} =C_{N} =0$。

当载荷为单向水平载荷时

(1) 表面应力边界条件$(z=0)$

(2) 层间结合条件$(z=z_{i} )$

此外,定解条件还有$A_{N}=C_{N} =F_{N} =0$,理由 同前。

以上诸式中$z_{i} =\sum\limits_{j=1}^i {h_{j} } $为第$i$层和第$i+1$层的界面的$z$坐标(参看图1); $K_{i} $称为第$i$层和第$i+1$层的界面的层间结合系数,$0\leqslant K_{i} <\infty {\begin{array}{*{20}c} \\ \end{array} }(i=1,2,\cdots\!,N-1)$。当$K_{i} \to \infty $时,$u_{i+1} =u_{i} $,$v_{i+1} =v_{i} $,层间完全连续;当$K_{i} =0$时,$\tau_{zri} =\tau _{zri+1} =0$,$\tau_{z\theta i} =\tau_{z\theta i+1} =0$,层间完全光滑;当$0<K_{i} <\infty $时层间结合状况介于上述两种极端状况之间,处于半结合状况。

2.3.2 BISAR程序

BISAR程序进行力学计算所采用的定解条件与上述NESCP程序所采用的定解条件基本一致,仅 式(4)和式(6)中水平位移与水平剪应力的关系式分别修改为

式(7)中$AK_{i}$称为界面剪切弹簧系数,$0\leqslant AK_{i} <\infty\ (i=1,2,\cdots\!, N-1)$。当$AK_{i} =0$时,$u_{i} =u_{i+1}\ v_{i} =v_{i+1} $,层间完全连续;当$AK_{i} \to \infty $时,$\tau_{zri} =\tau_{zri+1} =0$, $\tau_{z\theta i} =\tau_{z\theta i+1} =0$,层间完全光滑;当$0<AK_{i} <\infty$时层间处于半结合状况。

由上述可知：

(1)当层间处于半结合状况时,NESCP程序中采用的水平位移与水平剪应力的关系式是严格按照哥德曼(Goodman)法则的表达式,即

$\begin{eqnarray*} \tau =K\Delta u \end{eqnarray*}$

得到的,而BISAR程序中采用的关系式仍按照哥德曼法则的表达式但做了一点变化。

(2)在具体力学计算时,界面剪切弹簧系数$AK_{i} $与层间结合系数$K_{i}$实际上是互为倒数关系。

由于本文篇幅有限,下文仅介绍垂直载荷作用下$N$层弹性体系力学计算的有关内容。单向水平载荷作用下$N$层弹性体系力学计算的有关内容与此基本相似,请参看参考文献[14],不再一一叙述。将 式(1)中有关应力分量的表达式代入表面应力 边界条件式(3)并对每一个等式两边施加汉克尔积分变换^[15]即可得到两个方程式(写成矩阵形式)

将式(1)中有关力学分量的表达式代入层间结合条件式(4)并对每一个等式两边施加汉克尔积分变换^[15]即可得到($4N-4$)个方程式(写成矩阵 形式)

上述$4N-2$个方程式再加上$A_{N} =C_{N}=0$两个方程式,正好构成4$N$元线性代数方程组,用于求解4$N$个未知积分常数$A_{i}$,$B_{i}$,$C_{i}$,$D_{i}$ $\left( {i=1,2,\cdots\!,N} \right)$。

由多层弹性体系力学计算可知,如何从上述线性代数方程组快速地求算出积分常数,是保证快速计算出应力与位移分量数值的关键。在这一方面,中外学者们提出了不同的方法,一种是笔者提出的“递推回代法”并用于NESCP程序,另 一种是“传递矩阵法”,为BISAR程序所采用,现分别叙述如下。

2.5.1 用“递推回代法”求解积分常数

由前述可知,在垂直载荷作用下$N$层弹性体系求解积分常数的4$N$元线性代数方程组可以分成若干小组,其中由表面应力边界条件得到的两个方程式构成一个小组,由每一个层间界面上的四个层间结合条件得到的四个方程式分别构成$N-1$个小组。如果能利用这一特性建立相邻结构层积分常数的递推关系式,则4$N$元线性代数方程组的求解问题就可以简化成若干个四元乃至二元线性代数方程组的求解问题,从而大大简化计算。笔者提出的“递推回代法”正是基于这一思路,而“传递矩阵法”也是基于 这一思路。“递推回代法”的具体过程,简单来说就是先以各个小组为单位,将式(8)和式(9)内的$B_{i}$,$D_{i} $表示成以$A_{i}$,$C_{i}$ ($i=1,2,\cdots\!,N$)为自变量的多项式函数表达式

其次,通过式(10)和式(11)中$i=1$的方程式小组以及式(11)中相邻层间界面的方程式小组$B_{i}$和$D_{i} $相等的关系,消去$B_{i}$,$D_{i}$(i=1,2,...,N-1),即可进一步建立$A_{i}$,$C_{i}$与$A_{i+1}$,$C_{i+1}$之间的递推关系式

利用该递推关系式以及$A_{N}$=$C_{N}$=$0$,从$i=N-1$开始通过自下而上逐层递推,求出所需的$A_{i} $和$C_{i} $,这就是递推过程;再将已求得的$A_{i} $和$C_{i} $回代到$B_{i} $和$D_{i} $的多项式函数表达式中,求出所需的$B_{i} $和$D_{i} $,这就是回代过程。

2.5.2 用“传递矩阵法”求解积分常数

现将“传递矩阵法”的求解过程(仍以垂直载荷作用下$N$层弹性体系为例)叙述如下：

由式(9)并记$[T_{i} ]_{4\times 4} =[K_{i} ]_{4\times 4}^{-1} [K_{i+1} ]_{4\times 4} $ (式中矩阵$[T_{i} ]$称为传递矩阵),则可得到

又记 $[T]\!=\![T_{1} ][T_{2} ]\cdots[T_{N-1} ]$并利用$A_{N}\!=\!C_{N} =0$,即可得到第一层积分常数与第$N$层积分常数之间的关系式为

将式(14)代入式(8),得

求解时,首先利用式(15)确定$B_{N} $和$D_{N} $,然后利用式(13)和$A_{N} =C_{N} =0$,从第$N$层起逐层向上计算,直至计算出所需的$A_{i}$,$B_{i}$,$C_{i} $和$D_{i} $ 为止。

2.5.3 “递推回代法”与“传递矩阵法”的比较

首先,由于“传递矩阵法”的求算过程仍基于矩阵代数方法,在积分计算过程中需要频繁进行矩阵求逆或矩阵相乘运算,费时颇多;而“递推回代法”的求算过程完全成了普通的代数运算,比“传递矩阵法”省去了很多中间计算过程,从而大大节省了 计算时间。其次,“传递矩阵法”不能解决层间完全光滑时积分常数的求解问题。这是由于层间完全光滑时式(9)中的系数矩阵$[K_{i}]$为奇异矩阵(有一行元素全部为零),其对应的逆矩阵$[K_{i}]^{-1}$不存在。而“递推回代法”对层间完全连续、层间完全光滑和层间半结合时积分常数的求解问题都能解决。第三,由BISAR程序的计算可知,采用“传递矩阵法”进行矩阵运算时,有时会出现“病态矩阵”并导致计算结果很不精确。 而“递推回代法”不会出现“病态矩阵”。

由式(1)和式(2)可知,$N$层弹性体系应力与位移分量积分表达式的被积函数中包含贝塞尔函数和指数函数多项式两个部分。通过上述积分常数的求解和计算,被积函数中指数函数多项式部分已完全可以计算。下面再进一步介绍被积函数中贝塞尔函数的计算。在NESCP程序和BISAR程序中一般采用计算方法中的逼近多项式和逼近公式计算贝塞尔函数,前者采用阿伦(Allen)逼近公式,后者采用切比雪夫(Chebyshev)逼近公式,二者的计算精度和计算时间基本一致,前者稍佳。由于本文篇幅有限,下面仅介绍阿伦逼近公式。在NESCP程序中计算第一类零阶和一阶贝塞尔函数${\rm J}_{0} (x)$和${\rm J}_{1} (x)$的计算公式,如式(16)和式(17)所示。

当$x\leqslant 3$时,令$t=({x}/{3})^{2}$,${\rm J}_{0} (x)$和${\rm J}_{1} (x)$的逼近多项式为

当$x>3$时,令$t={3}/{x}$,${\rm J}_{0} (x)$和${\rm J}_{1} (x)$的逼近公式为

其中$A_{0}$,$B_{0}$,$A_{1}$,$B_{1} $采用的逼近多项式为

$\begin{array}{l}A_{0}=0.79788456-0.00000077 t-0.0055274 t^{2}-\\\begin{array}{l}0.00009512 t^{3}+0.00137237 t^{4}-0.00072805 t^{5}+ \\0.00014476 t^{6}\end{array}\\B_{0}=0.78539816+0.04166397 t+0.00003954 t^{2}-\\0.00262573 t^{3}+0.00054125 t^{4}+0.00029333 t^{5}-\\0.00013558 t^{6}\\A_{1}=0.79788456+0.00000156 t+0.01659667 t^{2}+\\0.00017105 t^{3}-0.00249511 t^{4}+0.00113653 t^{5}-\\0.00020033 t^{6}\\B_{1}=0.78539816-0.12499612 t-0.0000565 t^{2}+\\0.00637879 t^{3}-0.00074348 t^{4}-0.00079824 t^{5}+\\0.00029166 t^{6}\end{array}$

由式(1)和式(2)可知,$N$层弹性体系的应力与位移分量表达式都是含贝塞尔函数和指数函数的复杂被积函数的无穷积分,一般只能通过数值积分并采用有限数值的积分上限进行计算。在前人工作的基础上,笔者通过数学推导和误差分析,得到了如下述的积分计算公式(为简单明了起见,未写出应力与位移分量表达式积分号前的系数和无穷积分式大方括号外面的三角函数)和积分上限$x_{\rm s} $的计算公式并用于NESCP程序。

(1)积分计算公式

当$z\geqslant h_{1} $时

当$z<h_{1} $时,除了计算$0\sim x_{\rm s}$的积分值之外,还要加上相应的积分余项的值

以上二式中,$z$为计算点的$z$坐标,$h_{1} $为多层弹性体系第一层的厚度,${\rm J}(x)$表示各力学分量积分表达式中被积函数的贝塞尔函数部分,$E(x)$表示被积函数的指数函数多项式部分,$e(x)$是当弹性体为半无限弹性体时$E(x)$的表达式,积分$\int_0^{x_{\rm s} } {{\rm J}(x)E(x){\rm d}x} $和$\int_0^{x_{\rm s} } {{\rm J}(x)[E(x)-e(x)]{\rm d}x} $采用高斯(Gauss)求积公式,利用数值积分计算出,而积分$\int_0^\infty {{\rm J}(x)e(x){\rm d}x} $则采用列普司切兹$\!-\!$汉克尔(Lipschitz-Hankel)积分公式计算出^[16]。

(2)积分上限计算公式

其中$\delta $为载荷圆半径,$z$,$ h_{1} $的意义同式(19)。

试算表明,当积分上限$x_{\rm s} $取式(20)计算且在$0\sim x_{\rm s}$积分区间内设置足够多的数值积分结点时,即可满足计算结果至少精确到小数点后四位数。

由于保密,国外文献中从不介绍积分计算公式的内容,但根据对有关资料和对比算例的综合分析可知,BISAR程序的积分计算公式与上述NESCP程序基本一致,主要不同之处在于NESCP程序的积分上限$x_{\rm s}$是由式(20)通过计算确定的,而BISAR程序的积分上限$x_{\rm s}$是数值积分过程中根据计算精度分析确定的,见下文2.8节数值积分中所述。

在NESCP程序中笔者采用高斯$\!-\!$勒让德求积公式对各应力与位移分量表达式进行数值积分,在利用式(20)计算出积分上限$x_{\rm s}$后,首先将积分区间[0,$x_{\rm s}$]划分成长度相等的$m$个子区间,每个子区间上采用34结点高斯$\!-\!$勒让德求积公式计算其积分值,然后再将$m$个子区间的积分值相加,得到整个积分区间上的积分值。试算表明,在通常情况下当使用由式(20)得到的积分上限$x_{\rm s} $且$m$取3$\sim$5时,应力与位移分量的计算结果与国内外已公开发表的计算结果或者完全一致,或者十分接近并且满足计算结果至少精确到小数点后四位数。

在BISAR程序中各应力与位移分量表达式的数值积分过程为：

由式(1)和式(2)可知,各力学分量表达式都含有贝塞尔函数,贝塞尔函数是一个波动衰减函数,在积分区间[0,$x_{\rm s}$]内有很多零点。BISAR程序中的数值积分是在原点($x=0$)到第一个贝塞尔函数乘积的零点($x=z_{1}$)以及在后续的一个贝塞尔函数乘积的零点($x=z_{n}$)到下一个贝塞尔函数乘积的零点($x=z_{n+1}$) ($n=1,2,\cdots$)之间的区间上进行的。在第一个区间[0,$z_{1}$]上,采用8结点高斯$\!-\!$勒让德求积公式计算区间的积分值。从第二个区间开始,采用4$\sim$15结点高斯$\!-\!$洛巴多(Lobatto)求积公式计算每一个区间的积分值。设$INT$为 累计积分值,在积分计算过程中,如果连续两个贝塞尔函数乘积的零点之间的区间上积分的绝对值小于$10^{-5}$ (当$\vert INT\vert <0.01$)或区间上的积分值与$INT$之比的绝对值小于$10^{-4}$(当$\vert INT\vert \geqslant 0.01$),则积分计算结束。

当计算积分常数的矩阵运算过程中出现病态矩阵,数值积分会过早地停止并显示中止的原因。

由上述可知,NESCP程序数值积分过程简单明了,而BISAR程序则细致繁复,这大大增加了数值积分计算的时间。除此之外,在BISAR程序积分过程中,当由于出现病态矩阵使得数值积分过早停止时,将导致数值积分的结果很不精确。

以上内容介绍了在单圆载荷作用下$N$层弹性体系的应力与位移计算,在BISAR程序和NESCP程序中,后续的力学计算还有如下几项。

(1) 将各单圆载荷在计算点处产生的柱坐标中的应力与位移分量变换成公共直角坐标中的应力与位移分量,再通过求和得到多圆载荷作用下在计算点处产生的公共直角坐标中的总应力与总位移分量并利用弹性力学公式进一步计算出公共直角坐标中的总应变分量;

(2) 计算主应力及其方向余弦和主应变;

(3) 计算极值剪应力、极值剪应变及其相应正应力以及它们的方向余弦;

(4) 计算弹性体内每单位体积的总应变能和畸变应变能。

由于本文篇幅有限,上述后续力学计算的计算公式和计算过程请参看参考文献[14, 17-20]的有关论述,本文不再一一介绍。

计算算例是一个如图1所示的$N$等于5的五层弹性体系,表面承受单圆均布垂直载荷或单向水平载荷的作用。由于本文篇幅有限,下文仅列出该算例用NESCP程序和BISAR程序分别计算的在单圆均布垂直载荷或单向水平载荷作用下,各计算点处产生的 柱坐标应力与位移分量。

(1)五层弹性体系的结构参数

五层弹性体系的结构参数如表1所示。

(2)载荷计算参数

载荷计算参数如表2所示。

(3)数值计算结果

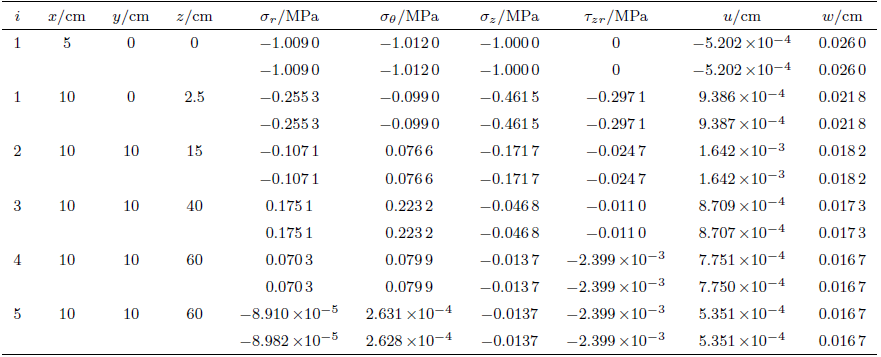
第一个载荷即垂直载荷单独作用时数值计算结果如表3所示(表中从左至右依次为计算点所在的层数$i$,计算点的$x$,$y$,$z$坐标,柱坐标应力与位移分量。每个计算点的计算数据的第一行为NESCP程序的计算结果,第二行为BISAR程序的计算结果)

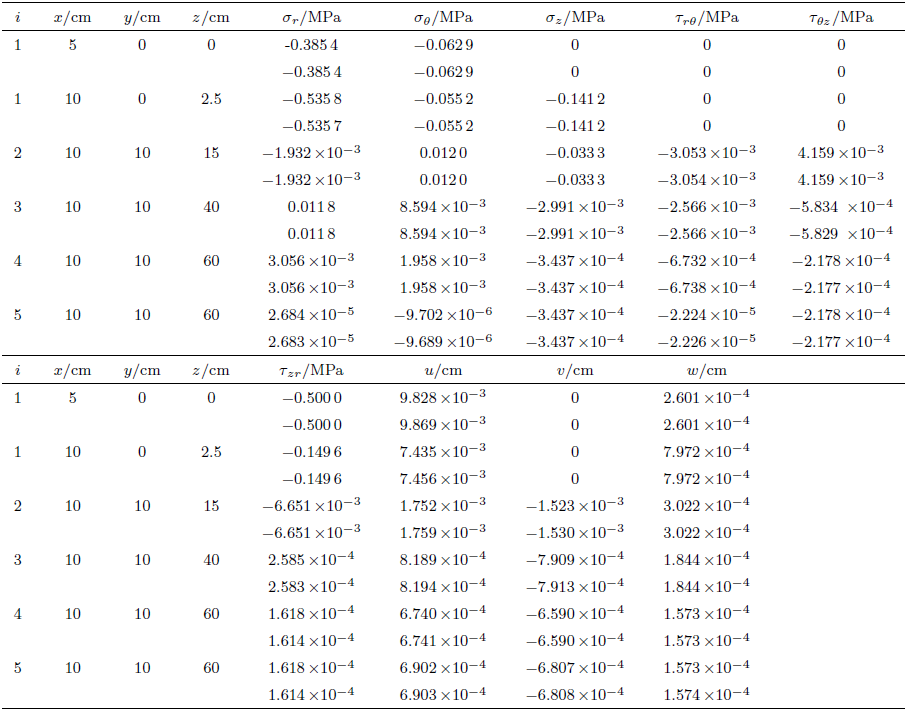
第二个载荷即单向水平载荷单独作用时数值计算结果如表4所示(表中从左至右依次为计算点所在的层数$i$,计算点的$x$,$y$,$z$坐标,柱坐标应力与位移分量。每个计算点的计算数据的第一行为NESCP程序的计算结果,第二行为BISAR程序的计算结果)。

由两个程序的对比计算结果可知,绝大多数对比数据完全一致,少数对比数据虽不完全一致,但十分接近(小数点后至少前4位数据能保持一致)。

如本文开头所述,层状弹性体系力学是多层柔性路面、机场道面以及多层地基设计与计算的理论基础。该理论及在其基础上所编制的各种实用程序在世界各国的上述工程结构的科学研究以及设计与计算中得到了广泛的应用。

以BISAR程序为例,英荷壳牌石油公司在最初编写BISAR程序时,对BISAR程序的使用功能作了两点定位：一是多层弹性体系通用力学计算程序,二是为壳牌路面设计方法SPDM (shell pavement design mothod)编制路面设计图表。自1973年BISAR程序问世以来,该程序为世界各国的路面与机场道面的科学研究和工程设计与计算做出了重大的贡献。

同样笔者编写的NESCP程序从20世纪80年代开始,为我国的路面与机场道面的科学研究也做出了很大的贡献,先后计算了几十万个数据。笔者在NESCP程序的基础上编制了多个公路和城市道路沥青路面设计程序, 服务于我国交通建设事业和高校教学。到目前为止,这些程序已在全国几百个设计单位和高校得到了成功应用,取得了显著的社会经济效益。

(1) 本文是迄今国内第一次以论文的形式全面、系统地向国内广大读者宣传、介绍层状弹性体系力学及其应用,让层状弹性体系力学发扬光大并得到新的更大的发展。层状弹性体系力学包含了丰富的内容而本文篇幅有限,为了比较深入和全面地了解层状弹性体系力学,笔者建议有兴趣的读者可以进一步阅读参考文献[14]。

(2) BISAR程序是当今世界上最负盛名的多层弹性体系力学计算程序。本文第二节对笔者编写的NESCP程序和BISAR程序的力学计算公式和计算方法进行了系统的对比。对比结果表明,NESCP程序的功能不仅可以与BISAR程序相媲美,而且在某些方面甚至更优越。本文用事实证明,外国人能做到的,中国人通过努力也一定能做到,而且还可能做得更好。