直升机舱门不均匀分布气动载荷加载方法研究

doi:10.6052/1000-0879-20-446

直升机舱门不均匀分布气动载荷加载方法研究

李玉莲^,¹⁾, 袁胜弢

哈尔滨飞机工业集团有限责任公司飞机设计研究所,哈尔滨 150066

ASYMMETRIC DISTRIBUTED AERODYNAMIN LOADS ON HELICOPTER DOOR

LI Yulian^,¹⁾, YUAN Shengtao

Aircraft Design & Research Institute, AVIC Harbin Aircraft Industry Group Co. LTD, Harbin 150066, China

通讯作者: 1)E-mail:liyulian1980@163.com

责任编辑: 王永会

收稿日期: 2020-10-19 网络出版日期: 2021-06-08

Received: 2020-10-19 Online: 2021-06-08

作者简介 About authors

摘要

针对直升机舱门结构强度有限元力学分析中,不均匀分布气动载荷难以施加的问题,提出基于数学分析,采用最小二乘法,对直升机机身局部结构的气动压力点的压力值进行压力分布曲面拟合,快速得到所有有限元节点的压力值,并通过Patran分析软件前处理中的Field (域)功能实现对有限元节点快速加载。该方法对某型机舱门的不均匀分布气动载荷加载进行验证,结果表明该方法精度高,可快速实现不均匀分布载荷的施加,有效解决有限元仿真分析前处理中不均匀载荷的加载问题。

关键词： 有限元分析; 气动载荷; 最小二乘法; 有限元节点

Abstract

In order to solve the problem of asymmetric distributed aerodynamic loads on the helicopter door, a least squares method is used to fit the data of the existing pressure on the aerodynamic nodes of the helicopter door, and to calculate the pressure on the FEM nodes, by the use of the function of the patran field, to realize the quick loading on FEM nodes. This method is proved to be steady and reliable through the experiment of putting the asymmetric distributed aerodynamic load on the helicopter door. The asymmetric distributed aerodynamic loading on the surface can be implemented faster by using this method, and the FEM analysis with the asymmetric distributed load can be made effectively.

Keywords： FEM analysis; aerodynamic loads; least squares; FEM nodes

PDF (5566KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李玉莲, 袁胜弢. 直升机舱门不均匀分布气动载荷加载方法研究. 力学与实践, 2021, 43(3): 347-352 DOI:10.6052/1000-0879-20-446

LI Yulian, YUAN Shengtao. ASYMMETRIC DISTRIBUTED AERODYNAMIN LOADS ON HELICOPTER DOOR. MECHANICS IN ENGINEERING, 2021, 43(3): 347-352 DOI:10.6052/1000-0879-20-446

应力分析是直升机结构强度设计最重要的工作内容之一,随着商业分析软件的快速发展,有限元已经成为复杂结构应力分析中最重要的工具^[1]。结构强度有限元分析过程包括有限元前处理、求解计算和后处理。对于直升机舱门结构强度有限元分析前处理工作,气动载荷是分析设计工作中非常重要的载荷设计输入^[2]。在国内航空界大部分科研院所,气动载荷分布由载荷专业计算,结构强度分析专业在有限元的前处理工作中将该载荷模拟并施加在有限元模型节点(单元)上,以进行有限元的求解计算工作。在工程设计中,将不均匀分布气动载荷施加到有限元节点上是一项非常繁琐但又很重要的工作。截至目前,航空航天行业广泛应用的有限元分析软件如Patran/Nastran,Abaqus等,尽管提供了强大的有限元分析计算功能,但对于不均匀分布面载荷还不能自动实现加载。人工手动对有限元节点或者单元进行逐个加载,满足不了实际工程设计的需求,因为直升机结构强度设计中的载荷工况较多,而且有限元细节模型的节点数目非常庞大,逐个单元或者节点的加载方式严重影响载荷施加的效率以及质量。如何提高有限元分析前处理工作中加载的效率与质量成为国内外专家学者重视的问题。

为了解决有限元分析前处理中施加不均匀分布气动载荷这一难题,国内外出现了很多算法。目前航空领域针对翼面结构的气动载荷分布,常用的算法是"多点排"方法^[3],该方法以静力等效以及应变能最小为约束条件,将每一种气动载荷分配到结构有限元分析模型的节点上。林小夏等^[4]提出基于特征函数分布对不均匀载荷进行加载。王专利^[5]、徐建新等^[6]使用了"多点排"的计算方法。高尚君等^[7]提出基于弹簧悬臂梁模型最小变形能的气动载荷分配方法。张建刚等^[8]针对翼面结构提出薄板样条插值函数来计算节点压力值,这些算法能解决实际中的问题,但需要在结构有限元模型与气动模型之间建立一种载荷数据传递关系,这种传递关系通过样条矩阵来实现。这些方法都是基于数值插值分析,即每一次计算均要调用原始数据,增加了算法的时间以及复杂度,而针对直升机结构气动载荷如何实现快速加载、等效分配的方法比较少。

本文以直升机舱门强度设计的工程实际需求为出发点,根据已知气动模型节点的压力值,通过数学分析最小二乘法,拟合出压力分布曲面,由该曲面拟合函数计算得到结构有限元模型每一节点的压力值,并对数值回归性进行分析。通过该拟合压力分布曲面函数的方法,可以准确、快速地将直升机舱门的不均匀分布气动载荷分配施加到有限元节点上,以供直升机结构强度工程师参考。

1 直升机舱门气动载荷

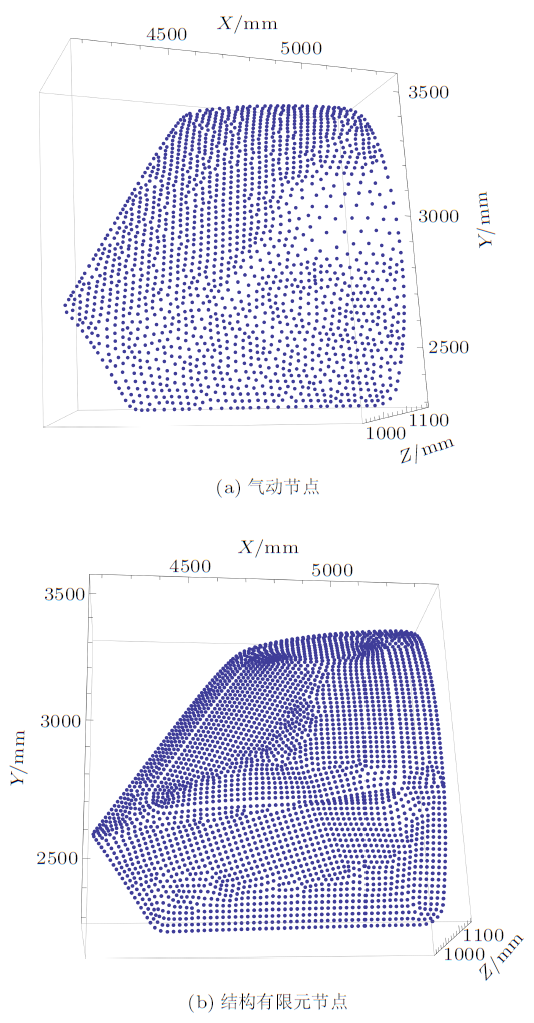
现代飞行器结构建模和气动模型普遍采用有限单元法^[9],两种模型划分是为了各自的分析任务而独立进行的。由于两种模型的分析目的不同,建模方式也存在很大的不同,以某型号直升机舱门为例,舱门的气动模型与结构分析有限元模型节点存在很大的差异。舱门气动模型的节点数为1892个,气动压力分布计算结果为1892组离散数据;而有限元模型为了保留结构边界,区分玻璃区域与结构区域,模型划分方法以及节点数目与气动模型均存在不同,两种模型的有限元节点差异对比如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 气动节点与结构有限元节点差异示意图

在舱门的结构强度分析有限元模型中,要实现施加不均匀分布的气动载荷,需要在结构有限元模型与气动模型之间建立一种载荷数据传递关系,工程上一般采用数值插值法或数据拟合法。数据拟合法根据气动载荷分布数据拟合出相对简单的数学模型,不需要每一个有限元节点的计算均调用原始气动分布数据,降低了算法时间和复杂度,拟合函数更逼近真实函数,本文中这种传递关系通过数学分析,采用最小二乘法拟合来实现^[10]。

2 最小二乘法基本理论

最小二乘法是一种基于已知离散点而拟合出近似函数的方法,使用离散点数据拟合得到曲面。最小二乘法具有拟合精度高、通用性强的特点。已知离散点函数(称为真实气动载荷)是单值连续的,则对空间区域$D$上的任何一个向量坐标点来说,理论上必有且只有一个确定的函数与之对应。由于在计算过程中真实函数是不知道的,任一向量所对应的函数值无法直接求出。为此,必须利用已知条件(有限元的节点以及气动载荷信息)构成一个逼近函数,用它来代替真实函数,借以计算任一向量所对应的函数的近似值。

假设空间区域$D$内,已知数值的$n$个数据点集$p_{i}$,其中$i=1,2,\cdots,n$,其坐标可以表示为$(x_{i}$, $y_{i}$, $z_{i})$,在$n$个节点$z_{i} =(x_{i},y_{i} )$有已知值

(1) $ \begin{eqnarray} \overline{\mathbf \varphi_{i} } =\overline{\mathbf \varphi} (x_{i} ,y_{i})\ \ (i=1,2,\cdots, n) \end{eqnarray} $

已知数值用矢量表示为

(2) $ \begin{eqnarray} \label{eq2} \mathbf \phi_{i} =\left\{ {{\begin{array}{c} {\phi_{1} } \\ {\phi_{2} } \\ \vdots\\ \phi_{m} \\ \end{array} }} \right\}_{i} (i=1,2,\cdots ,n) \end{eqnarray} $

设拟合函数$\mathbf \phi (z)=[b_{1} (z)\ \ b_{2} (z)\ \ \cdots \ \ b_{m} (z)]$。已知数值用矢量表示为

(3) $ \begin{eqnarray} \label{eq3} \left\{ {{\begin{array}{c} {\lambda_{1} (z)} \\ {\lambda_{2} (z)} \\ \vdots \\ {\lambda_{m} (z)} \\ \end{array} }} \right\}=\mathbf b^{\rm T}(z)\mathbf \lambda (z) \end{eqnarray} $

其中$b_{m} (z)$为$m$个线形无关的基函数,$\mathbf \lambda(z)$为$m$维系数矢量,是基函数的待定系数。最小二乘法即按照偏差平方和最小原则选取拟合曲线,在计算区域内,由式(3),利用加权最小二乘法构成二次形式

(4) $ \begin{eqnarray} \min \sum\limits_{i=1}^n {\mathbf \delta_{i}^{2} } =\min \sum\limits_{i=1}^n {\mathbf w(z)} \left[ {\sum\limits_{i=1}^n {\mathbf B\mathbf \lambda (z)-\overline {\mathbf \varphi} } } \right]^{2} \end{eqnarray} $

其中

(5) $ \begin{eqnarray} && \mathbf B=\left[ {{\begin{array}{*{20}c} {b_{1} (z_{1} )} & {b_{2} (z_{1} )} & \cdots & {b_{m} (z_{1} )} \\ {b_{1} (z_{2} )} & {b_{2} (z_{2} )} & \cdots & \\ \vdots & \vdots & & \vdots \\ {b_{1} (z_{n} )} & {b_{2} (z_{n} )} & \cdots & {b_{m} (z_{n} )} \\ \end{array} }} \right] \end{eqnarray} $

(6) $ \begin{eqnarray} \label{eq5} \mathbf w(z)=\left[ {{\begin{array}{*{20}c} {w_{1} (z-z_{1} )} & 0 & \cdots & 0 \\ {0} & {w_{2} (z-z_{2} )} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & {w_{m} (z-z_{n} )} \\ \end{array} }} \right] \end{eqnarray} $

基函数$b_{m} (z)$是已知的,为求得待定系数,式(4)中对$\mathbf \lambda(z)$一次求导等于0,求得

(7) $ \begin{eqnarray} \label{eq6} \mathbf \lambda (z)=[\mathbf B^{\rm T}{\mathbf w}(z)\mathbf B]^{-1}\mathbf B^{\rm T}\mathbf w(z)\overline {\mathbf \varphi} \end{eqnarray} $

从而求得拟合近似函数为

(8) $ \begin{eqnarray} \label{eq7} \mathbf \phi(z)=\mathbf b^{\rm T}(z)[\mathbf B^{\rm T}{\mathbf w}(z)\mathbf B]^{-1}\mathbf B^{\rm T}\mathbf w(z)\overline{\mathbf \varphi} \end{eqnarray} $

3 舱门气动分布拟合

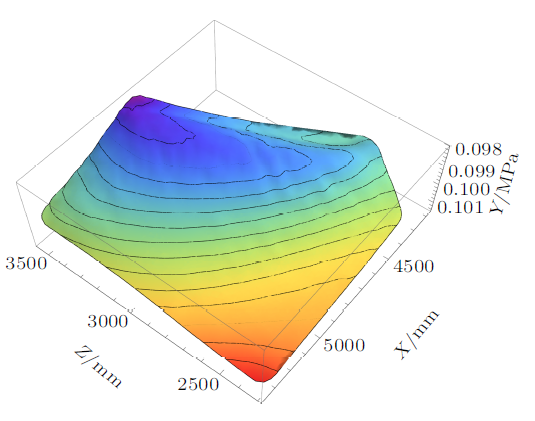
直升机舱门的气动载荷为不均匀的分布载荷,载荷专业提供的舱门压力为气动模型离散点的分布,在某型号直升机设计中,舱门某种状态的气动压力分布等高线分布图如图2所示。从图中可以看出,对于直升机舱门结构,沿着舱门纵向坐标$X$以及高度方向坐标$Z$的不同,气动压力分布呈现为非均布载荷。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 某型机舱门气动分布

舱门气动载荷拟合函数具有最小二乘法的性质,得到直升机在空中各种不同飞行状态时压力分布的逼近曲面函数。在计算过程中,待定系数的快速求解采用数学分析软件Mathematica中的程序进行^[11]。

分析计算中,有限元节点的坐标值参考坐标系为机身全局坐标系。舱门机身轴向向后为$X$坐标正向,机身高度向上为$Z$坐标正向。最小二乘法拟合函数可以是一次、二次函数等所有初等函数,在舱门的压力分布中,分别对平面分布和曲面分布进行多次拟合以及回归性分析,以计算校核逼近函数的精度。其中线性基拟合时,式(3)中$m$取3,基函数表达式为式(9);二次基拟合时,式(3)中$m$取6,基函数表达式为式(10);立方基拟合时,式(3)中$m$取10,基函数表达式为式(11)。

(9) $ \begin{eqnarray} \label{eq8} &&\mathbf b^{\rm T}=(1,x,z) \end{eqnarray} $

(10) $ \begin{eqnarray} \label{eq9} \mathbf b^{\rm T}=(1,x,z, x^{2},xz,z^{2}) \end{eqnarray} $

(11) $ \begin{eqnarray} \label{eq10} \mathbf b^{\rm T}=(1,x,z, x^{2},xz,z^{2},x^{3},x^{2}z,xz^{2},z^{3}) \end{eqnarray} $

当$m=3$时,舱门的压力分布载荷呈平面分布,基函数取二次以上时,舱门的压力分布为曲面分布。根据已知气动点的压力值求出逼近函数,进而求得有限元节点压力值。有限元软件Patran中有Field (域)加载功能,通过最小二乘法拟合,可快速实现不均匀分布载荷的施加处理过程。

4 舱门气动载荷拟合结果分析

4.1 数学分析与拟合

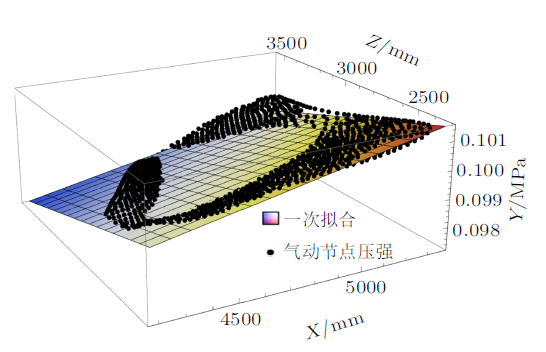
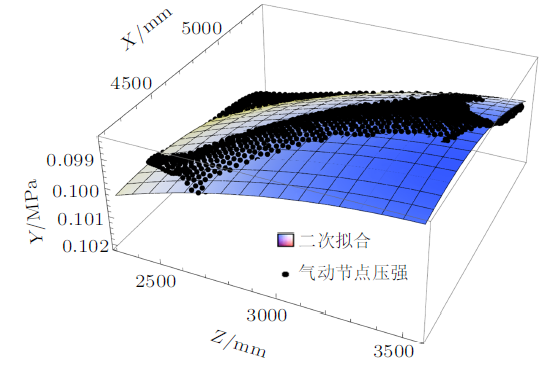
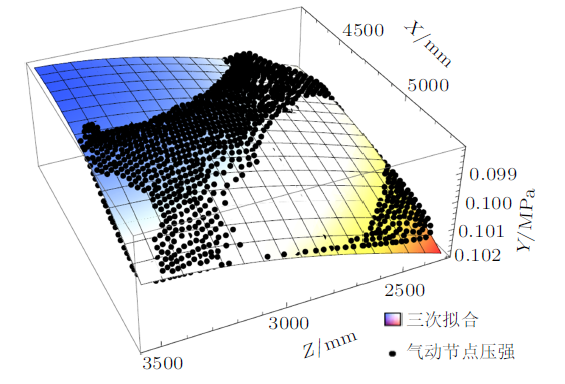
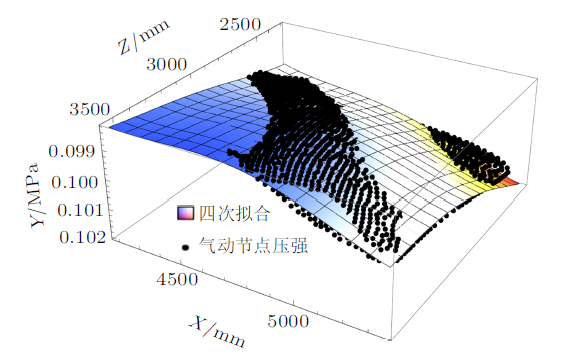
某型号直升机舱门的非均布气动分布载荷,当采用不同的基函数进行最小二乘法拟合时,确定系数如表1所示。图3$\sim\!$图6是不同基函数所计算得出的拟合函数与舱门原气动点压力值对比分析,从图4与图3的对比结果可以看出,随着拟合函数系数的增高,拟合后的压力曲面和拟合前的节点压力分布趋势一致,吻合程度逐渐提高,结合表1数据分析,从线性基到二次基的确定系数提高量最大,二次基后随着拟合函数次数提高,确定系数的数值区域增加得较为平缓。

表1 拟合误差分析表

新窗口打开| 下载CSV

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 舱门气动载荷数据与一次拟合曲面

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 舱门气动载荷数据与二次拟合曲面

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 舱门气动载荷数据与三次拟合曲面

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 舱门气动载荷数据与四次拟合曲面

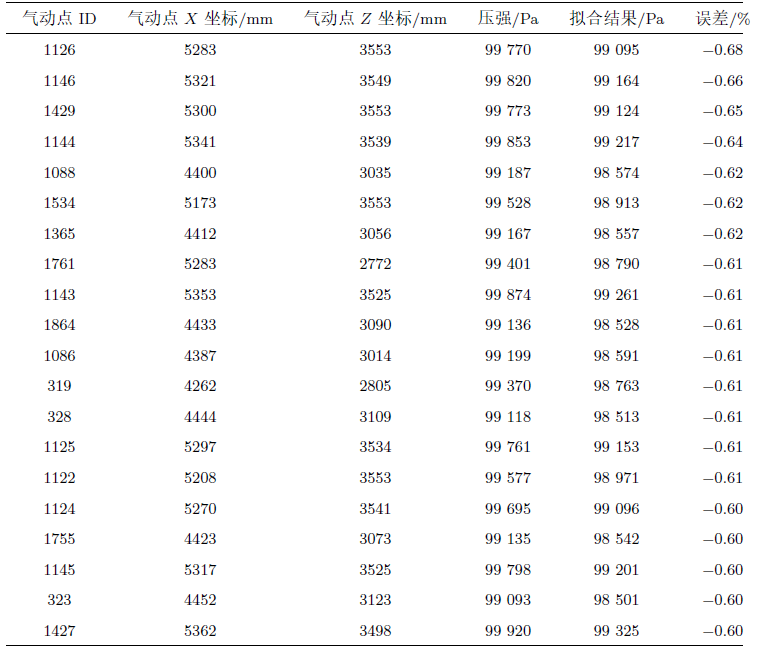
根据以上分析,二次基的拟合结果较为优异,当采用二次基函数拟合时,对气动节点进行拟合精度分析,计算结果见表2,拟合结果与原始数据的单点误差最大值小于1%,最小二乘法的曲面拟合结果具有较高精度,能够满足工程上的设计要求。

表2 拟合结果与气动节点压强对比分析表

新窗口打开| 下载CSV

4.2 拟合结果分析

从图6中可以看出,插值拟合的压力曲面和插值前的气动点压力分布吻合程度很好,通过这种数据传递方式,可以快速实现由气动模型的散点压力分布求出有限元节点的压力分布,进而通过逼近函数实现对有限元模型的快速加载。

5 结论

本文根据工程实际需求,基于气动离散点压力分布,通过最小二乘法拟合函数,可以实现直升机舱门压力载荷拟合加载,提高有限元分析中加载的效率,拟合加载的精度较高。

Mathematica程序中的数学理论清晰,编程拟合插值简单,可以有效解决工程中的实际问题。根据不同的工况,拟合逼近函数随着气动离散点压力分布的改变而改变,尤其针对直升机的飞行状态多变、压力分布多变的情况,插值拟合函数具有较好的适应性,对多工况可以实现快速方便地加载,对于主要承受不均匀分布的气动载荷的结构,提高了强度有限元分析的效率。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

孙侠生

. 飞机结构强度新技术. 北京: 航空工业出版社, 2017