据《墨子·鲁问》记载^[1],在楚越战争期间,由于越国位于楚国下游河流,越国失利可顺流而退。鲁班为帮助楚国发明了"钩强",以"钩"住逃跑的越国船只。后来,为了训练这一战术而形成了一种称之为"牵钩"的游戏。世界上许多国家都流行拔河,只是规则不同。1900-1920年之间,拔河曾是奥运会比赛项目,但因缺乏统一规则于1920年被取消^[2]。1960年,由英国、瑞典等国正式成立国际拔河联合会(Tug of War International Federation, TWIF),1965年开始举办欧洲锦标赛,1975年开始举办世界锦标赛。此后欧洲锦标赛和世界锦标赛每年交替进行。由牛顿第三定律知道,拔河双方所受的拉绳拉力始终相同,但同样的力施加于双方却产生出了不同的效果。李林等^[3]对拔河中队员运动分为平动和转动,通过受力分析比较了摩擦力与重力矩在拔河过程中的重要作用,但该分析没能对拔河运动的训练提出建议。本文仍将拔河队员运动分为平动和转动,补充讨论运动员身体倾角和拉绳倾角,以及手臂、腿部弯曲等因素对拔河比赛的影响,为拔河训练提供一些理论参考。

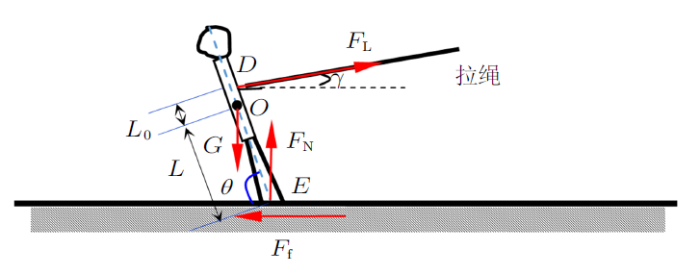
如图1所示为一对一拔河中一方的受力模型,为了简化,当人的姿态确定后将其视为刚体模型,受力包括：拉绳的拉力$F_{\rm L}$,地面对运动员的支撑力$F_{\rm N}$,重力$G$,摩擦力$F_{\rm f}$。并引入下列参数：拉绳与水平线的夹角$\gamma$,人体向后倾角$\theta$,人体重心$O$,绳拉力在人体上的作用点$D$,且$L_{0} =\left| {OD}\right|$,$L=\left| {OE} \right|$。

拔河过程可分为僵持阶段和运动阶段,运动阶段又可以分为平动和转动两种形式^[3]。考虑处于僵持阶段,列出平衡方程

水平方向

竖直方向

对$E$点的矩平衡

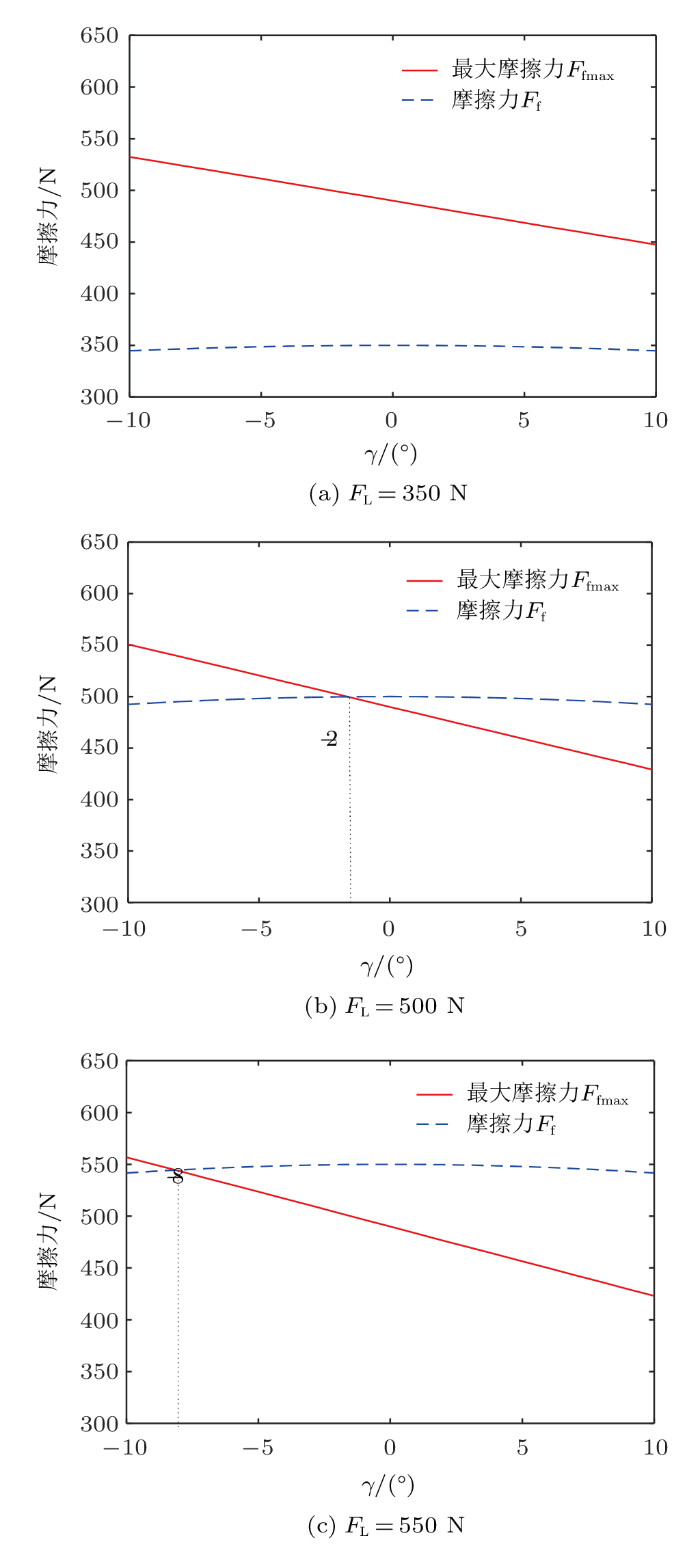
当双方用力拉动对方时,绳拉力由0逐渐增加,摩擦力也随之增加,当一方的摩擦力先达到最大静摩擦力时,也将先达到由僵持转向平动的临界状态,即

这里,$F_{\rm fmax } $表示最大静摩擦力,以$\mu$表示静摩擦因数,有$F_{\rm fmax } =\mu F_{\rm N} =\mu \left( {G-F_{\rm L} \sin \gamma } \right)$。一般情况下,$\gamma$取值很小,大约在$\left( {-10^\circ,10^\circ}\right)$之间,该区间内$F_{\rm fmax } $为减函数,意味着$\gamma $越小越有利于增加最大静摩擦力。从受力上看,当$\gamma <0$时,拉力$F_{\rm L}$使得正压力增加,也就增加了最大静摩擦力$F_{\rm fmax }$;相反,当$\gamma >0$时,拉力$F_{\rm L} $会减小正压力,从而减小最大静摩擦力$F_{\rm fmax }$。综合式(1)、式(2)和式(4),可知不被拉动时$\gamma $应满足条件

式(5)取等号时为临界状态。为了直观地观察$\gamma $的临界值,假定$G=700$ N,$\mu=0.7$,画出不同拉力作用下摩擦力随$\gamma $的变化曲线,如图2(a) $\sim\!$图2(c)所示。可见,当拉力较小时无论$\gamma$取何值都不会被拉动,如图2(a)所示。当拉力$F_{\rm L} =500$ N时,$\gamma =-2^\circ$为临界状态,如图2(b)所示。当拉力$F_{\rm L}=550$ N时,$\gamma =-8^\circ$为临界状态,如图2(c)所示。

拔河中的拉绳要么水平、要么倾斜。当拉绳水平时,双方的$\gamma$角均为0,此时$F_{\rm L} =\mu G$,如果双方体重和摩擦因数完全相同,将同时达到临界状态。当拉绳倾斜时,双方的$\gamma $角必然为一正一负、且大小相等。可以证明$\cos \gamma +\mu \sin \gamma $在$\left( {-10^\circ,10^\circ}\right)$之间为增函数,因此,在一定的拉力作用下,若我方$\gamma$取负,对方$\gamma$取正,对方将率先 超出条件(5),我方获胜机会增加。比赛中,一方队员一旦坐在地上就很容易被拉动,正是因为坐在地上时$\gamma$角较大,影响效果明显。

当最大静摩擦力足够大时,虽然拉力不能使运动员滑动却有可能拉动身体前倾,人为了确保身体平衡,会向前挪动脚步从而输掉比赛。身体前倾就是身体发生了转动,这一过程可以看作是绳拉力矩和重力矩的较量,将其分别记为

绳拉力矩

重力矩

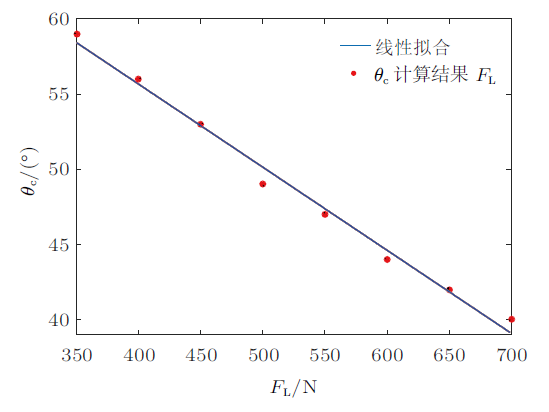
当$M_{\rm L} >M_{\rm G} $时就有可能输掉比赛。根据文献^[3],$\theta $的取值范围大致在$\left( {30^\circ,90^\circ}\right)$,该范围内$M_{\rm L} $为增函数($\gamma $取值很小),$M_{\rm G} $为减函数。身体后倾可使$\theta $取较小值,达到减小拉力矩、增大重力矩的目的。由式(3)可知,当拉绳倾角$\gamma$和拉力$F_{\rm L} $确定后,可求出身体发生转动的临界倾角,记为$\theta_{\rm c}$。当$\theta $小于$\theta_{\rm c}$时,拉力矩小于重力矩,将不会被拉动。设队员身高为1.78 m时,因重心大概位于人体高度的56%左右,近似有$L=1$ m,$L_{0}=0.2$ m,因$\gamma $很小,令其为0,拉力取值设定在350 N~700 N之间,求解不同拉力下的$\theta_{\rm c}$,如图3所示。显然,在该取值范围内,$\theta_{\rm c} $随拉力$F_{\rm L}$近似线性递减,这说明拉力越大,保持平衡所需的$\theta $就越小。不过,也应注意到身体倾角越小,有可能导致$\gamma$为正,从而减小最大静摩擦力。因此,需要综合考虑$\theta $和$\gamma $的取值。

最后,在拔河中弯曲手臂肘部紧贴腰部,拉力作用点位于腰部,而将手臂展开拉力沿着手臂作用,作用点在肩部,这说明$L_{0}$可以通过弯曲和伸展手臂调整。同时$L$也可以通过微弯腿部来调整。由式(6)和式(7)可以看出,减小$L_{0}$也就减小了绳拉力矩的力臂,从而减小拉力矩。微弯腿部减小$L$虽然同时减小了拉力矩和重力矩,不过腿部微弯后再蹬地,由于身体后倾,可将腿部力量转换为拉绳的拉力,这相比于手臂拉力可大大增加$F_{\rm L}$的值,因此微弯腿部虽然会损失重力矩,但有利于蹬地发力,可将腿部力量转化为拉力从而增加对抗力量。

本文通过建立一对一的拔河模型,分析了拉绳倾角$\gamma $,身体倾角$\theta$,以及身体姿态对拔河比赛的影响规律。结果表明抬高拉绳,使我方拉力斜向下时有利于增大我方最大静摩擦力,并减小对方最大静摩擦力;较小的身体倾角有利于减小拉绳拉力矩、增加重力矩,但需要综合考虑拉绳倾角的影响;从运动员的姿态考虑,手臂应弯曲后紧贴腰部以减小拉力矩;腿部微弯虽然会导致拉力矩和重力矩同时减小,但通过脚蹬地,可将腿部力量转化为拉力$F_{\rm L}$,间接影响比赛结果。在实际比赛中,虽然上述各量的可调整范围都非常小,但如果力量相当时,适时地根据对方的姿态和状况做出有利于我方的调整,恰当的运用力学原理,微弱的优势也会成为取胜的关键。

责任编辑: 胡漫