理论力学教具DIY系列(四)一个教具的受力分析与讨论

理论力学教具DIY系列(四)一个教具的受力分析与讨论

高云峰^,¹⁾

清华大学航天航空学院, 北京100084

通讯作者: 1)E-mail:gaoyunfeng@tsinghua.edu.cn

责任编辑: 胡漫

收稿日期: 2020-02-14 网络出版日期: 2021-02-08

Received: 2020-02-14 Online: 2021-02-08

作者简介 About authors

PDF (2473KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

高云峰. 理论力学教具DIY系列(四)一个教具的受力分析与讨论. 力学与实践[J], 2021, 43(1): 94-99 DOI:

受力分析是理论力学教学中的重要内容,而多点摩擦问题是其中的难点。在目前的教学安排中,静力学有少量求解多点摩擦的习题,学生可以画图、列出方程并求解;但是在动力学中,几乎没有涉及多点摩擦的习题,而且也不要求解方程。

一个实际问题如何简化为力学模型、如何分析列出方程、如何求解、如何验证,是工科学生必需掌握的基本技能。当然一门课程不可能教会学生处理实际问题的所有环节或流程,但在适当的情况下让学生了解这一过程,让部分感兴趣的学生深入探究,还是有可能的。因此我在教学中有意识地设计了一些教具,让学生有机会分析处理一个"完整问题"——问题的简化、分析、计算、制作模型验证。

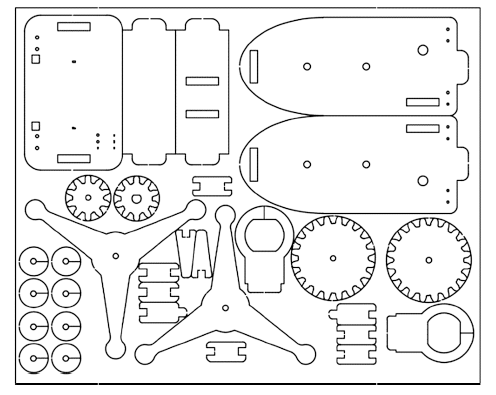
1 实际问题:一个小巧的力学演示装置

这是一个专门设计的装置(图1),利用激光切割后,加上减速电动机、电池和开关,就可以拼装出一个爬行装置,且装置尾巴长度可调(图2)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 爬行装置的设计图

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 实际的爬行装置

为了突出"完整问题"的分析过程而不陷入复杂的计算,可以通过调整重心位置让装置在平面内运动。观察发现,装置的运动状况依赖于它的尾长:短尾时轮子一部分时间打滑,一部分时间不打滑,装置前进得比较慢;长尾时轮子不打滑,前进得稍快些。

定性解释很容易:尾长影响重心相对位置,导致尾部和轮子处的压力不同。尾短时重心靠近尾部,轮子处压力小会打滑;尾长时重心靠近轮子,轮子处压力大不会打滑。

但是具体分析计算就复杂得多,轮子旋转时,轮子和尾部受到的压力、摩擦力与装置的加速度和角加速度有关,不容易直观判断哪一点会打滑。为了进行具体的分析计算,首先就需要建立一个力学模型。

2 力学模型:如何合理简化?

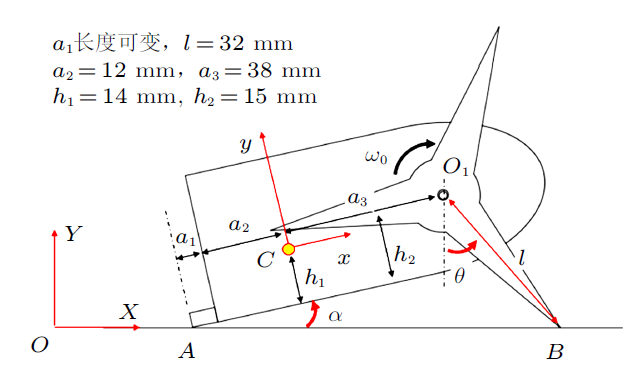
设$OXY$是地面参考坐标系,$Cxy$是随体坐标系,$C$是装置主体(不包轮子)的质心,任意时刻,尾巴$A$和轮子边缘$B$接触地面。装置的几何尺寸参数为:尾巴长度$a_{1}$;质心距离尾部$a_{2}$,距离底部$h_{1} $,轴心$O_{1} $距离尾部$a_{2} +a_{3}$,距离底部$h_{2}$;轮长为$l$ (图3)。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 装置的力学模型

装置分为两部分,主体和轮子。设主体质量为$m_{1}$,轮子质量为$m_{2}$;主体质心$C$的坐标为$x_{C}$,$y_{C}$;车身俯仰角度为$\alpha$ (绕$z$轴);观察发现车轮以匀角速度$\omega_{0} $顺时针转动,设$t$时刻$\theta=\pi/3 -\omega_{0} t$,因此$\theta \in (-\pi /3, \pi/3)$为某轮接触地面时的角度范围。由于$A$、$B$始终接触地面,可以得到$\alpha$与轮子转角$\theta $的关系,根据轴心$O_{1}$距离水平面的高度,有

(1)$\begin{eqnarray} (a_{1} +a_{2} +a_{3} )\sin \alpha +h_{2} \cos \alpha =l\cos \theta \end{eqnarray} $

从式(1)解出$\alpha $,求导后$\dot{{\alpha }}$、$\ddot{{\alpha}}$也都已知。类似可以得到$y_{C}$, $y_{O1} $与$\alpha $或$\theta$的关系。

为了保证装置能正常运动,轮子长度需要满足2个条件:(1) $l\cos (\pi/3) >h_{2}$,保证轮子总能接触地面;(2)轮子不能太长,保证重心总落在$A$、$B$之间,否则装置会翻倒。

3 数学模型

装置在平面内运动时,涉及的运动参数有$x_{C}$, $y_{C}$, $\alpha $,力参数有$F_{A}$, $N_{A}$, $F_{B}$, $N_{B}$。注意到装置中$A$、$B$两点接触地面,哪点会打滑是多点摩擦问题中的难点。通常假设某点不打滑,然后得到计算结果,再判断结果是否合理。在本问题中,存在三种模式。

3.1 模式一(假设$A$不动,$B$打滑)

设$t$时刻$A$点坐标$x_{A} (t)=x_{A}^{* }$, $y_{A}=0$已知,根据图3,其他各点的坐标为

(2)$\left.\begin{array}{l} x_{C} =x_{A} +(a_{1} +a_{2} )\cos \alpha -h_{1} \sin \alpha\\ y_{C} =(a_{1}+a_{2} )\sin \alpha +h_{1} \cos \alpha \end{array}\right\} $

(3)$\left.\begin{array}{l} x_{O1} =x_{C} +a_{3} \cos \alpha -(h_{2} -h_{1} )\sin \alpha\\ y_{O1}=y_{C} +a_{3} \sin \alpha +(h_{2} -h_{1} )\cos \alpha \end{array}\right\} $

(4)$x_{B} =x_{O1} +l\sin \theta,\ \ y_{B} =y_{O1} -l\cos \theta $

相应各点速度、加速度都可以求出,从而各点的位置、速度、加速度都是已知函数。

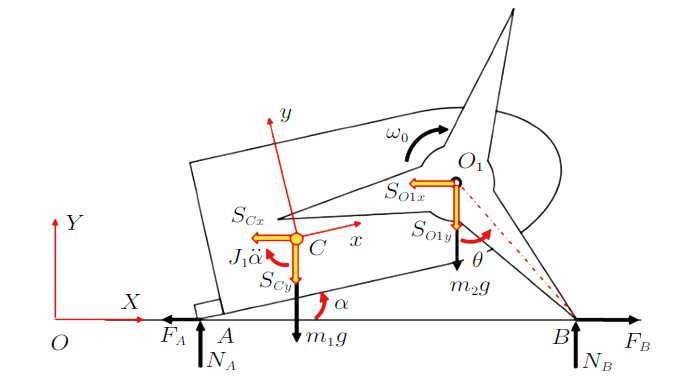
根据受力图(图4),利用动静法,可以列出$X$和$Y$方向力的平衡方程、$B$点打滑的摩擦力补充方程、对$A$点力矩的平衡方程,为

(5)$\begin{eqnarray} \left. {\begin{array}{l} -m_{1} \ddot{{x}}_{C} -m_{2} \ddot{{x}}_{O1} -F_{A} +F_{B} =0 \\ -m_{1} \ddot{{y}}_{C} -m_{2} \ddot{{y}}_{O1} +N_{A} +N_{B} -\\\qquad m_{1} g-m_{2}g=0 \\ F_{B} =\mu N_{B} \\ -J_{1} \ddot{{\alpha }}+N_{B} x_{AB} -m_{1} (g+\ddot{{y}}_{C} )x_{AC} -\\\qquad m_{2} (g+\ddot{{y}}_{O1} )x_{AO1} +m_{1} \ddot{{x}}_{C} y_{C} +\\\qquad m_{2} \ddot{{x}}_{O1} y_{O1} =0 \\ \end{array}} \right\} \end{eqnarray} $

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 装置的受力分析

这时方程(5)中所有的运动学参数都是已知量,因此是代数方程,容易解出。

解出后要验证是否满足(1)所有压力、摩擦力均大于0;(2) $F_{A} \leqslant \mu N_{A} $是否成立。如果条件都满足,说明模式一假设成立($A$不动,$B$打滑),然后对$t+\Delta t$时刻进行计算;否则说明模式一不成立,转入模式二。

3.2 模式二(假设$B$不动,$A$打滑)

设$t$时刻$B$点坐标$x_{B} (t)=x_{B}^{* }$,$y_{B}=0$已知,根据图3,其他各点的坐标为

(6)$x_{O1} =x_{B} -l\sin \theta ,\ \ y_{O1} =l\cos \theta $

(7)$\left.\begin{array}{l} x_{C} =x_{O1} -a_{3} \cos \alpha +(h_{2} -h_{1} )\sin \alpha\\ y_{C}=y_{O1} -a_{3} \sin \alpha -(h_{2} -h_{1} )\cos \alpha \end{array}\right\} $

(8)$\left.\begin{array}{l} x_{A} =x_{C} -(a_{1} +a_{2} )\cos \alpha +h_{1} \sin \alpha\\y_{A} =y_{C} -(a1+a2)\sin \alpha -h_{1} \cos \alpha \end{array}\right\} $

相应各点的速度、加速度都可以求出,从而各点的位置、速度、加速度都是已知函数。

根据受力图(图4),利用动静法,系统方程为

(9)$\begin{eqnarray} \left. {\begin{array}{l} -m_{1} \ddot{{x}}_{C} -m_{2} \ddot{{x}}_{O1} -F_{A} +F_{B} =0 \\ -m_{1} \ddot{{y}}_{C} -m_{2} \ddot{{y}}_{O1} +N_{A} +N_{B} -\\\qquad m_{1} g-m_{2} g=0 \\ F_{A} =\mu N_{A} \\ -J_{1} \ddot{{\alpha }}-N_{A} x_{AB} +m_{1} (g+\ddot{{y}}_{C} )x_{CB} +\\\qquad m_{2} (g+\ddot{{y}}_{O1} )x_{O1B} +m_{1} \ddot{{x}}_{C} y_{C} +\\\qquad m_{2} \ddot{{x}}_{O1} y_{O1} =0 \\ \end{array}} \right\} \end{eqnarray} $

方程(9)也是代数方程,解出后要验证是否满足(1)所有压力、摩擦力均大于0;(2) $F_{B}\leqslant \mu N_{B}$是否成立。如果条件都满足,说明假设模式二成立($B$不动,$A$打滑),然后对$t+\Delta t$时刻进行计算;否则说明模式二不成立,转入模式三。

3.3 模式三(假设$A$、$B$均打滑)

在这种模式下$\ddot{{x}}_{C}$,$\ddot{{x}}_{O1}$成为未知量,利用运动学关系把$\ddot{{x}}_{O1} $用$\ddot{{x}}_{C}$表示,因此得到一组微分代数方程

(10)$\begin{eqnarray} \left. {\begin{array}{l} (m_{1} +m_{2} )\ddot{{x}}_{C} +F_{A} -F_{B} =f_{1} (\alpha ,\dot{{\alpha }},\ddot{{\alpha }}) \\ N_{A} +N_{B} =f_{2} (\alpha ,\dot{{\alpha }},\ddot{{\alpha }}) \\ (m_{1} y_{C} +m_{2} y_{O1} )\ddot{{x}}_{C} -N_{A} x_{AB} =f_{3} (\alpha ,\dot{{\alpha }},\ddot{{\alpha }}) \\ F_{A} -\mu N_{A} =0 \\ F_{B} -\mu N_{B} =0 \\ \end{array}} \right\} \end{eqnarray} $

方程(10)中$f_{1}$, $f_{2}$, $f_{3} $是$\alpha$, $\dot{{\alpha}}$, $\ddot{{\alpha}}$的函数,5个方程5个未知数,可以求解。求解结束后要验证是否满足(1)所有压力、摩擦力均大于0;(2) $F_{A} \leqslant \mu N_{A} $,$F_{B} \leqslant \mu N_{B}$是否成立。如果条件都成立说明假设模式三成立($A$和$B$都打滑),然后对$t+\Delta t$时刻进行计算;否则说明公式或程序中可能存在错误,要返回检查。

但是如何求解微分代数方程,需要一些技巧,在下面数值计算中会介绍。

4 数值计算

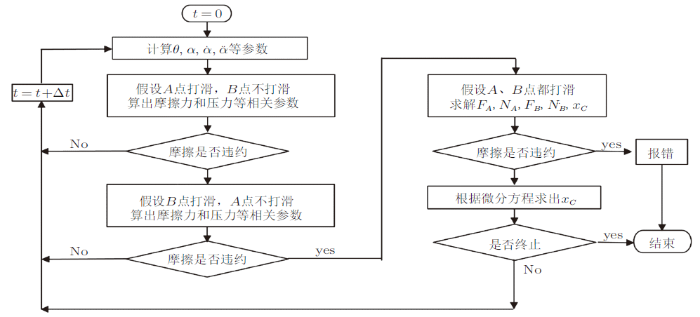
有了方程,可以算出装置运动和受力随时间变化规律,然后把数据进行可视化处理。数值求解前通常先要画出计算框图,考虑各种可能情况(图5)。下面采用Matlab程序进行计算,可以在计算结束后直观从屏幕上查看虚拟装置如何运动,方便与实际装置进行比较。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 求解方程的计算框图

Matlab程序采用矩阵和列阵计算很方便,可以把前面的方程统一改写为$AX=B$的形式,例如方程(10)改写为

(11)$\begin{eqnarray} &&\left[ {{\begin{array}{*{20}c} 1 & 0 & {-1} & 0 & {(m_{1} +m_{2} )} \\ 0 & 1 & 0 & 1 & 0 \\ 0 & {-x_{AB} } & 0 & 0 & {(m_{1} y_{C} +m_{2} y_{O1} )} \\ 1 & {-mu} & 0 & 0 & 0 \\ 0 & 0 & 1 & {-mu} & 0 \\ \end{array} }} \right]\cdot\\&&\qquad\left( {{\begin{array}{*{20}c} {F_{A} } \\ {N_{A} } \\ {F_{B} } \\ {N_{B} } \\ {\ddot{{x}}_{C} } \\ \end{array} }} \right)=\left( {{\begin{array}{*{20}c} {f_{1} (\alpha ,\dot{{\alpha }},\ddot{{\alpha }})} \\ {f_{2} (\alpha ,\dot{{\alpha }},\ddot{{\alpha }})} \\ {f_{3} (\alpha ,\dot{{\alpha }},\ddot{{\alpha }})} \\ 0 \\ 0 \\ \end{array} }} \right) \end{eqnarray} $

在模式一、模式二中,调用$X={\rm inv}(A)^* B$的命令格式就完成了求解。但模式三的微分代数方程处理起来要复杂一些:先把$\ddot{{x}}_{C}$当作代数量,用$X={\rm inv}(A)^* B$求解出来,设解出$\ddot{{x}}_{C}=\ddot{{x}}_{C}^{*}$ (这时$\ddot{{x}}_{C}^{*}$是具体数值),再把$\ddot{{x}}_{C}=\ddot{{x}}_{C}^{*}$当作微分方程,化为标准的一阶微分方程组后,直接调用荣格库塔法(Runge-Kutta methods)求解常微分方程。

具体过程是:设$t$时刻系统各个参数(位置、速度)都已经算出,现在要通过微分方程$\ddot{{x}}_{C}=\ddot{{x}}_{C}^{*}$计算出$t+\Delta t$时刻的参数。设$y_{1}=x_{C} $,$y_{2} =\dot{{y}}_{1}$,这样就把二阶微分方程化为标准的一阶微分方程组以及相应的初始条件,为

(12a)$\left. {\begin{array}{l} \dot{{y}}_{1} =y_{2} \\ \dot{{y}}_{2} =\ddot{{x}}_{C}^{* } \\ \end{array}} \right\}$

(12b)$\left. {\begin{array}{l} y_{1} (0)=x_{C} (t) \\ y_{2} (0)=\dot{{x}}_{C} (t) \\ \end{array}} \right\}$

积分时间段为$[t,t+\Delta t]$,求解常微分方程调用的格式为

(13)$ [t,iy]=ode45('rg{\_}kt', [time,time+hh],y0,options); $

程序式(13)中参数按顺序含义为:"t"是存放积分时间;"iy"是存放积分结果;"ode45"是求解常微分方程的标准函数;"rg_kt"是微分方程表达式的子函数;"[time, time+hh]"是积分时间段;"y"是初始值;"options"是积分的误差选项。

值得说明的是,考虑到数值计算存在误差,因此在判断摩擦关系是否违约时要稍微放松一点要求,假设.积分允许误差为$\varepsilon =1.0\times 10^{-6}$,则把摩擦关系$F\leqslant \mu N$放松为

(14)$\begin{eqnarray} F\leqslant (1+\varepsilon )\mu N \end{eqnarray} $

数值计算得到的结果符合定性分析的结论,但是有更多细节。下面是装置在一个周期内($\theta \in [-\pi/3, \pi/3]$)各参数变化的情况。

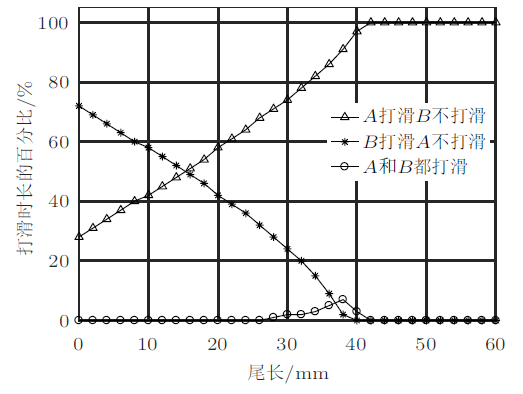
图6表明了尾长与各点打滑时长的关系:(1)尾巴越长,$A$点打滑时间越多;存在一个临界尾长$a_{1}^{*}$,$a_{1} \geqslant a_{1}^{* }$时$A$点始终打滑。(2)大部分情况下装置不会出现$A$和$B$都打滑的情况,只在临界尾长附近才会出现,且存在的时间都很短,在实际中不容易观察到。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 尾长与打滑时长的关系

图7显示了$a_{1}=5$ mm时主体质心加速度的变化,一方面看出模式转换时加速度会有跳变,另一方面可以看出质心加速度比重力加速度小3个数量级,因此可以认为装置运动是"准静态"过程,从而可以从静力学角度近似估计出$a_{1}^{*} $:如果轮子在$x$方向距离质心最远时有$N_{B} \geqslant N_{A} $,则$A$点会一直要打滑。分别对图4中的$A$和$B$取矩,有

(15)$\begin{eqnarray} \left.\begin{array}{l} N_{A} x_{AB} =m_{1} g\bigg[ l\sin \dfrac13\pi +a_{3} \cos \alpha_{0} -\\\qquad \left( {h_{2} -h_{1} } \right)\sin \alpha_{0} \bigg]+m_{2} gl\sin \dfrac13\pi \\ N_{B} x_{AB}\!=\!m_{1} g\left[ {\left( {a_{2}\! +\!a_{1} } \right)\cos \alpha_{0} \!-\!h_{1} \sin \alpha_{0} } \right]+\\\qquad m_{2} g\left[ {\left( {a_{1} +a_{2} +a_{3} } \right)\cos \alpha_{0} -h_{2} \sin \alpha_{0} } \right] \\ \end{array} \right\} \end{eqnarray} $

考虑到实际上$\alpha $是小量,从式(15)中近似得到

(16)$\begin{eqnarray} a_{1}^{* } \approx l\sin \dfrac13\pi -a_{2} +(m_{1} -m_{2} )a_{3} /(m_{1} +m_{2} ) \end{eqnarray} $

代入装置的数据,得到$a_{1}^{* } \approx39$ mm,接近图6中的40 mm。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 尾长与质心加速度的关系

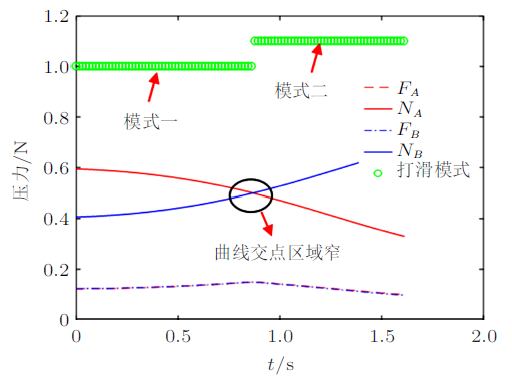
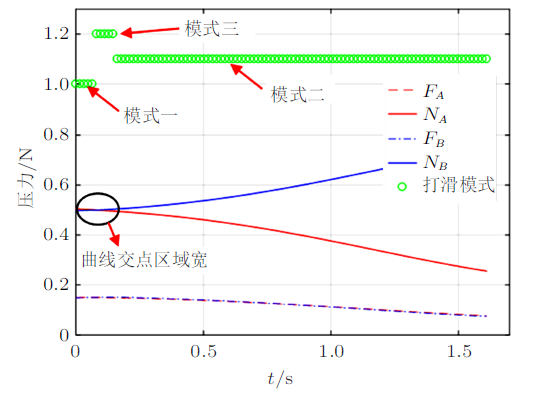
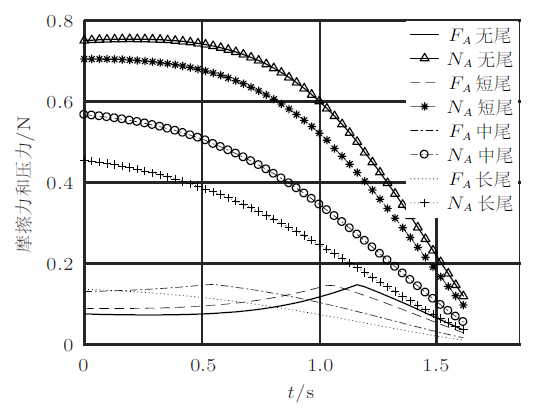
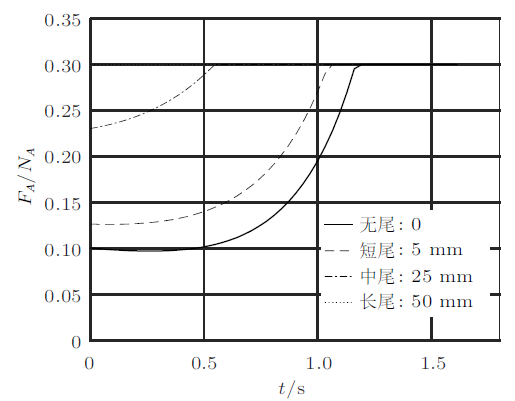
为什么在临界尾长$a_{1}^{*}$附近才会出现$A$和$B$均打滑的情况? 从图8和图9中可以看出,当$A$和$B$压力曲线有交点时,会出现模式转换。当压力曲线交点区域较窄时(斜率大),只在模式一和模式二间进行转换,不会出现模式三;当压力曲线交点区域较宽时(斜率小),三种模式都会出现。这可以理解为:临界尾长$a_{1}^{*}$的装置在$t\to 0$时,$A$和$B$压力就很接近,此时质心速度很小,数值计算时不能一步跨出这个区域,就会出现$A$和$B$都打滑这种模式。在非临界尾长情况下,若$A$和$B$压力接近,此时质心速度较大,数值计算时可以一步跨出这个区域,不会出现$A$和$B$都打滑的状况。