再生混凝土是利用再生骨料部分或全部替代天然骨料拌制的混凝土,可再次应用于建筑结构或者市政工程,实现资源的可持续利用,同时可有效解决废弃建筑垃圾造成的环境污染及资源浪费等问题,实现建筑垃圾的重复利用。虽然再生混凝土的力学性能低于普通混凝土,但研究证明,其仍然有应用于建筑结构的价值[1 ] 。
基于断裂理论,材料力学研究分为宏观、细观、微观及纳观四个层次[2 ] 。宏观层次上,再生混凝土的非均质性较普通混凝土更为复杂,通常被认为由再生粗骨料、新硬化水泥砂浆、老硬化水泥砂浆、老粘结带、新粘结带五相材料组成。各国学者对再生混凝土的基本力学性能或钢组合构件性能进行了大量研究,取得了丰富的成果[3 -6 ] 。但由于材料来源不确定性、骨料形状及宏观试验环境等随机因素的影响,针对同一问题,不同学者基于不同试验目的结论离散程度较高[1 ] 。基于细观层次理论的混凝土数值模拟方法,可以有效避免宏观试验各因素的不利影响,同时可弥补宏观试验时观察混凝土内部微裂纹开展及演变过程较为困难的不足,为混凝土等材料性能的研究提供了新思路。
基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] 。Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能。研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响。Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究。数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增。Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度。研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带。
本文基于势能原理的基面力元法[18 -19 ] ,以单元边界长度与单元的外法向量的乘积为基本元素,通过利用连续介质学理论推导四边形单元应变及刚度矩阵显式表达式,可解决ANSYS,ABAQUS等常规有限元软件需要构造位移插值函数及借助高斯积分才能求解刚度矩阵等限制,适用于任意坐标系任意平面及空间单元静力及动力分析[20 -21 ] 。
本文根据再生混凝土的细观结构特征,建立五种不同再生骨料取代率(0%,30%,50%,70%及100%)的二维圆形及任意凸多边形随机骨料模型,基于基面力元法研究单轴载荷作用时混凝土内部微裂纹的演变过程、断面破坏形态与再生骨料取代率、分布及形状的关系。
1 基面力
对于任意二维弹性体区域,$P$和$Q$表示物质点变形前和变形后的径矢。$x^{\alpha}\left(\alpha =1,2\right)$为物质点Lagrange坐标,物质点位移为
(1) $\begin{eqnarray} {u}={Q}-{P} \end{eqnarray} $
(2) $\begin{eqnarray} {P}_{\alpha } =\frac{\partial {P}}{\partial x^{\alpha }},\ \ {Q}_{\alpha } =\frac{\partial {Q}}{\partial x^{\alpha }} \end{eqnarray} $
(3) $\begin{eqnarray} {u}_{\alpha } =\frac{\partial {u}}{\partial x^{\alpha }} =Q_{\alpha } -{P}_{\alpha } \end{eqnarray} $
假定物质点为小变形,Green应变张量${\varepsilon }$为
(4) $\begin{eqnarray} {\varepsilon }=\frac{1}{2}\left( {u_{\alpha } \otimes P^{\alpha }+P^{\alpha }\otimes u_{\alpha } } \right) \end{eqnarray} $
如图1 所示,为描述$Q$点的应力状态,在向量d$x{Q}_{1}$, ${\rm d}x{Q}_{2} $上作四边形微元,d${T^1}$, d${T^2}$表示对应边上的力,约定:$2+1=1$,$1-1=2$。则定义
(5) $\begin{eqnarray} {T^\alpha }=\frac{1}{{\rm d}x^{\alpha +1}{\rm d}x^{\alpha -1}}{\rm d}{T^\alpha } \end{eqnarray} $
图1
则$T^{\alpha}$ $(\alpha =1,2)$为Lagrange坐标系$x^{\alpha}$ $(\alpha =1,2)$中$Q$点的基面力。
基于"基面力"概念,Cauchy应力张量可通过式(6)表达
(6) $\begin{eqnarray} {\sigma }=\frac{1}{A_{Q}}T^{\alpha }\otimes Q_{\alpha } \end{eqnarray} $
(7) $\begin{eqnarray} T^{\alpha }=\rho A_{Q} \frac{\partial W}{\partial u_{\alpha } }=\rho_{0} A_{P} \frac{\partial W}{\partial u_{\alpha } } \end{eqnarray} $
式中,$\rho$和$\rho_{0} $为物质点变形前后的物质密度,$W$为物质点应变能密度。
由式(7)可知,位移梯度$u_{\alpha}$为基面力$T^{\alpha}$的共轭变量。因此,由$u_{\alpha } $与$T^{\alpha }$可以描述所有力学问题。
2 四边形基面力模型
假定任意$x^{\alpha }\left( {\alpha =1,2}\right)$坐标系中,任意一个考虑边界位移协调问题的四边形单元,$I,J,K,L$表示单元节点编码,${u^I},{u^J},{u^K},{u^L}$表示单元节点位移,如图2 所示。
图2
2.1 单元应变
(8) $\begin{eqnarray} \overline{\varepsilon} =\frac{1}{A}\int_A {{\varepsilon} {\rm d}V} \end{eqnarray} $
将Green应变张量$\varepsilon $代入单元平均应变,则单元平均应变为
(9) $\begin{eqnarray} \overline {\varepsilon} =\frac{1}{2A}\int_A {\left( {u_{\alpha } \otimes P^{\alpha }+P^{\alpha }\otimes u_{\alpha } } \right){\rm d}A} \end{eqnarray} $
(10) $\begin{eqnarray} \overline{\varepsilon} =\frac{1}{2A}\int_S {\left( {u\otimes n+n\otimes u} \right){\rm d}S} \end{eqnarray} $
式中,$S$为四边形单元边界,$n$为外法线矢量。
(11) $\begin{eqnarray} \overline{\varepsilon} =\frac{1}{2A}\sum\limits_{i=1}^4 {L_{i} \left( {u_{i} \otimes n_{i} +n_{i} \otimes u_{i} } \right)} \end{eqnarray} $
式中,$L_{i} \left( {i=1,2,3,4} \right)$为边界长度,$n_{i} \left({i=1,2,3,4} \right)$为边界线外法线向量,$u_{i} \left( {i=1,2,3,4}\right)$为边界线几何中心点位移向量。
假定变形过程中,边界线始终保持直线状态,则边界线几何中心点的位移向量$u_{i}$为
(12) $\begin{eqnarray} u_{i} =\frac{1}{2}\left( {u_{I} +u_{J} } \right) \end{eqnarray} $
式中,$u_{I} ,u_{J} $表示边界线节点$I,J$位移向量。单元应变可表示为
(13) $\begin{eqnarray} \overline{\varepsilon} =\frac{1}{2A}\left( {u_{I} \otimes m^{I}+m^{I}\otimes u_{I} } \right) \end{eqnarray} $
(14) $\begin{eqnarray} m^{I}=\frac{1}{2}\left( {L_{IJ} n^{IJ}+L_{IK} n^{IK}} \right) \end{eqnarray} $
式中,$L_{IJ} ,L_{IK} $为边界长度;$n^{IJ},n^{IK}$为边界外法线向量。
2.2 单元刚度矩阵
(15) $\begin{eqnarray} W_{D} =\frac{AE}{2\left( {1+\nu } \right)}\left[ {\frac{\nu }{1-2\nu }\left( {\overline {\varepsilon} :U} \right)^{2}+\overline{\varepsilon} :\overline{\varepsilon} } \right] \end{eqnarray} $
式中,$\nu $为泊松比,$E$为弹性模量。将单元应变$\overline \varepsilon $代入应变能公式(15),得
(16) $\begin{eqnarray} &&W_{D} =\frac{E}{4A\left( {1+\nu } \right)}\bigg[ \frac{2\nu }{1-2\nu }\left( {u_{I} \times m^{I}} \right)^{2}+ \left( {u_{I} \cdot u_{J} } \right)m^{IJ}+\left( {u_{I} \cdot m^{J}} \right)\left( {u_{J} \cdot m^{I}} \right) \bigg] \end{eqnarray} $
式中,$m^{IJ}=m^{I}\cdot m^{J}$。则作用在单元$I$节点的力为
(17) $\begin{eqnarray} f^{I}=\frac{\partial W_{D} }{\partial u^{I}}=K^{IJ}u_{J} \end{eqnarray} $
(18) $\begin{eqnarray} &&K^{IJ}=\frac{E}{2A\left( {1+\nu } \right)}\bigg( \frac{2\nu }{1-2\nu }m^{I}\otimes m^{J}+ m^{IJ}U+m^{J}\otimes m^{I} \bigg) \end{eqnarray} $
3 再生混凝土二维随机骨料模型
3.1 骨料颗粒数
根据瓦拉文公式[22 ] ,试件内骨料粒径$D<D_{0} $的累积分布概率为
(19) $\begin{eqnarray} P_{\rm c} (D<D_{0} )=P_{\rm k} \bigg[ 1.065\left( {\frac{D_{0} }{D_{\max } }} \right)^{1/2}- \\ 0.053\left( {\frac{D_{0} }{D_{\max } }} \right)^{4}- 0.012\left( {\frac{D_{0} }{D_{\max } }} \right)^{6} -\\ 0.0045\left( {\frac{D_{0} }{D_{\max } }} \right)^{8}-0.0025\left( {\frac{D_{0} }{D_{\max } }} \right)^{10} \bigg] \end{eqnarray} $
式中,$P_{\rm c} $为粒径小于$D_{0} $的骨料累积分布概率;$P_{\rm k}$为骨料与试件面积比,取0.75;$D_{\max } $为最大骨料直径。
基于瓦拉文级配曲线,确定100mm$\times$100mm, 150mm$\times$150mm及300mm$\times$300mm试件内随机骨料等效粒径及颗粒数,如表1 所示。
3.2 网格映射
根据瓦拉文公式获得各粒径骨料颗粒数后,建立骨料储存库,通过逐粒提取、逐粒投放方法将骨料库内的骨料投放到指定断面内,建立随机骨料分布模型。随后,建立四边形背景网格,并映射到随机骨料分布模型。根据四边形节点与骨料圆心或形心的相对位置判别该四边形的属性,判别规则及步骤如下:
(2)四边形的四个节点全部位于骨料内部,则该单元为骨料;
(3)剩余的新砂浆单元中,若四边形的四个节点中至少存在1个节点,且至多存在3个节点位于骨料内部,则该单元为老粘结带;
(4)剩余的新砂浆单元中,若四边形的四个节点全部位于附着砂浆内部,则该单元为附着砂浆单元;
(5)剩余的新砂浆单元中,若四边形的四个节点至少存在1个节点,且至多存在3个节点位于附着砂浆内部,则该单元为新粘结带单元。
以取代率为50%的凸多边形骨料模型为例,网格映射过程如图3 所示。
图3
再生混凝土有限元模型中各项介质的分布如图4 所示。图4 清晰地描述再生混凝土有限元模型中各项介质的分布,表明本文采用的骨料投放技术及网格映射技术可以用来建立和表征再生混凝土内部复杂的非均质复合材料的特性。
图4
3.3 圆形随机骨料模型
基于蒙特卡洛随机算法,生成两个伪随机数$R_{n}$, $E_{n} (0<R_{n}, E_{n}<1)$确定骨料圆心坐标$\left( {x_{n} ,y_{n} } \right)$。
(20) $\begin{eqnarray} \left. {\begin{array}{l} x_{n} =R_{n} b \\ y_{n} =E_{n} l \\ \end{array}} \right\} \end{eqnarray} $
通过Fortran语言编写的二维圆形随机骨料生成软件,生成100 mm$\times$100 mm,150 mm$\times$150 mm及300 mm$\times$300 mm的再生混凝土细观模型,如图5 所示。
图5
3.4 凸多边形随机骨料模型
基于圆形随机骨料模型,根据最小基框架长度限定条件及面积等值规则,在圆形骨料圆周上生成基框架并向外部延伸,建立任意凸多边形随机骨料模型。
为避免基框架延伸后形成凹型骨料,基框架延伸点$P_{j}(x,y)$与延伸直径两节点$A_{i}(x_{i},y_{i})$, $A_{i+1}(x_{i+1},y_{i+1})$组成三角形$P_{j} A_{i} A_{i+1}$的面积应满足$S_{P_{j}} <0$。
为避免新骨料侵入已投放骨料,基框架延伸点$P_{j} \left( {x,y}\right)$与延伸直径相邻基框架节点组成的三角形$P_{j} A_{i-1} A_{i} $、$P_{j}A_{i+1} A_{i+2} $的面积应满足$S_{P_{j} } >0$。
(21) $\begin{eqnarray} S_{P_{j} } =\frac{1}{2}\left| {{\begin{array}{c@{\quad }c@{\quad }c} x & y & 1 \\ {x_{i} } & {y_{i} } & 1 \\ {x_{i+1} } & {y_{i+1} } & 1 \\ \end{array} }} \right| \end{eqnarray} $
为避免骨料相互侵入,运用式(21)对新插入延伸点$P_{j} \left( {x,y}\right)$与已投放凸多边形骨料各边组成的三角形面积进行判断,至少存在一个三角形面积$P_{j}A_{n} A_{n+1} <0$。
通过Fortran语言编写的二维任意凸多边形随机骨料生成软件,生成100 mm $\times$ 100 mm,150 mm $\times$ 150 mm及300 mm$\times$300 mm的再生混凝土细观模型,如图6 所示。
图6
3.5 不同取代率随机骨料模型
根据150 mm$\times$150 mm再生混凝土细观结构特征,建立骨料取代率为0%,25%,50%,70%及100%的二维圆形及任意凸多边形随机骨料模型,如图7 所示。
图7
4 再生混凝土单轴受压数值模拟
4.1 材料损伤模型
细观数值模拟过程中,材料的损伤本构模型对材料的载荷响应行为具有重要的影响。作为非均质复合材料,没有统一且特定的损伤本构模型来描述再生混凝土在载荷作用下的损伤行为。基于试验及理论研究,弹塑性模型[23 ] 、非均匀强化塑性模型[24 ] 、塑性模型[25 ] 、塑性断裂模型[26 ] 、Ottosen模型[27 ] 、Darwin-Pecknold模型[28 ] 、Stankow-Gerstle模型[29 ] 及过-徐模型[30 ] 等一系列数学模型被提出以描述混凝土的细观力学行为。本文基于最大拉应力强度准则,通过多折线损伤模型[20 ] 表征五相介质在位移载荷作用下的力学行为,如图8 所示。
图8
(22) $\begin{eqnarray} E=E_{0} \left( {1-D} \right) \end{eqnarray} $
式中,$E$为当前状态下的弹性模量,$E_{0}$为初始弹性模量,$D$为材料损伤因子,表达式为
(23) $\begin{eqnarray} D_{\rm t} =\left\{ \begin{array}{l} 0, \qquad {\varepsilon \leqslant \varepsilon_{\rm t0} } \\ {1-\dfrac{\varepsilon_{\rm t0} }{\varepsilon }+\dfrac{\varepsilon -\varepsilon_{\rm t0} }{\eta_{\rm t} \varepsilon_{\rm t0} -\varepsilon_{\rm t0} }\dfrac{\varepsilon_{\rm t0} }{\varepsilon }\left( {1-\alpha } \right)}, \\\qquad {\varepsilon_{\rm t0} <\varepsilon \leqslant \eta_{\rm t} \varepsilon_{\rm t0} } \\ {1-\dfrac{\alpha }{\xi_{\rm t} -\eta_{\rm t} }\dfrac{\varepsilon -\eta_{\rm t} \varepsilon_{\rm t0} }{\varepsilon }+\dfrac{\alpha \varepsilon_{\rm t0} }{\varepsilon }}, \\\qquad {\eta_{\rm t} \varepsilon_{\rm t0} <\varepsilon \leqslant \xi_{\rm t} \varepsilon_{\rm t0} } \\ 1, \qquad {\varepsilon >\xi_{\rm t} \varepsilon_{\rm t0} } \\ \end{array} \right. \end{eqnarray} $
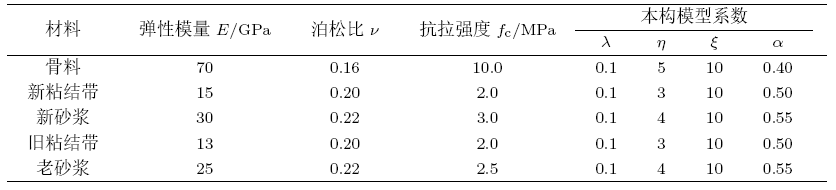
式中,$\varepsilon_{\rm t0} $ 为峰值应变;$f_{\rm t} $ 为抗拉强度;$\lambda$,$\eta$,$\xi$分别为弹性应变、残余应变及极限应变系数;$\alpha$为强度系数,如表2 所示。
细观层次上,再生混凝土的结构特征可通过五相介质描述。因此,其力学性能受到五相介质基本力学参数的影响。Xiao等[13 ] 研究发现,骨料的弹性模量介于40$\sim$100 GPa,新砂浆及附着砂浆弹性模型介于17.5$\sim$40 GPa,新旧粘结带的弹性模量介于9.2$\sim$25.0 GPa。同时,试验表明[13 ,31 -33 ] ,新粘结带及旧粘结带的弹性模量为新砂浆及附着砂浆弹性模量的50%$\sim$80%。而粘结带作为骨料与砂浆之间的薄弱传力层,力学性能及粘结性能较差,因此本文取50%。结合文献[13 , 31 -33 ],本文数值模拟时,五相介质的力学参数取值如表2 所示。
4.2 内部破坏裂纹
为了研究载荷作用下,试件内部裂纹的萌生及延伸,本文建立试件尺寸为150 mm$\times$150 mm的随机骨料模型,将圆形及任意凸多边形随机骨料模型映射到四边形网格背景,单元尺寸为1.0 mm,运用基于基面力概念不同取代率的再生混凝土损伤程序,采用位移控制模式进行单轴加载,步长为0.005 mm/步。
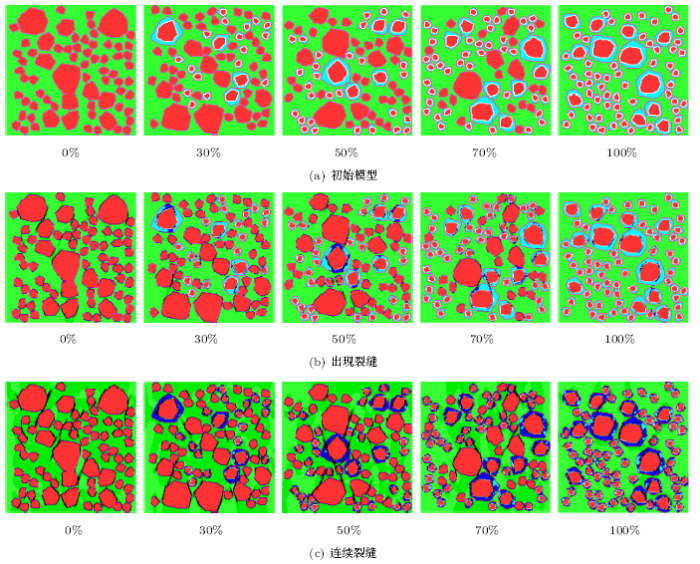
圆形随机骨料断面内微裂纹产生及延伸过程如图9 所示。可以看出,圆形随机骨料模型在加载过程中,内部微裂纹首先出现在粘结带区域,且裂纹较离散。随着位移载荷逐渐增加,新老粘结带裂纹之间的老砂浆应力增大,随后发生破坏,在骨料周围形成局部破坏裂缝,此时试件达到峰值应力。载荷继续增加,骨料之间的新砂浆应力逐渐增大,随后发生破坏,骨料之间形成斜向45$^\circ$的连续破坏裂缝。
图9
图9
不同取代率的圆形再生混凝土单轴压缩裂缝开展过程
随着再生骨料取代率的增加,内部微裂纹的首次出现位置逐渐由新粘结带向旧粘结带转移。当再生骨料取代率低于50%时,试件内部沿斜向45$^\circ$形成1$\sim$2条连续破坏裂缝,且裂缝宽度较小。当再生骨料取代率超过50%时,试件内部沿双向45$^\circ$形成多条V型连续破坏裂缝,且裂缝宽度逐渐增加。
骨料密集区域新砂浆含量低于其他区域,骨料周围形成局部破坏裂缝后,骨料之间传递应力的新砂浆含量较少,局部应力远高于其他区域,因此试件内部连续破坏裂缝主要集中在骨料密集区域。随着骨料取代率的增加,断面内薄弱区域增多,连续破坏裂缝向再生骨料密集区域过渡,且裂缝路径容易受到骨料分布的影响。
任意凸多边形随机骨料试件内部微裂纹产生及延伸过程如图10 所示。可以看出,任意凸型随机骨料模型在加载过程中,内部微裂纹首先出现位置、骨料周围局部裂缝与圆形随机骨料模型类似。但是加载过程中任意凸型骨料尖端位置存在应力集中现象,因此局部裂缝首先沿骨料各边发展,随后与其他骨料的局部裂缝贯通形成连续破坏裂缝。由于受到骨料形状的影响,试件内部局部裂缝更离散,连续破坏裂缝数量多于圆形随机骨料模型。
图10
图10
不同取代率的凸型再生混凝土单轴压缩裂缝开展过程
4.3 单轴抗压强度
试件尺寸为100 mm及150 mm的圆形骨料及任意凸型骨料再生混凝土单轴抗压强度如表3 所示。
由表3 可知,随着再生骨料取代率的增加,再生混凝土的峰值应力逐渐递减。当再生骨料取代率低于50%时,峰值应力下降速率较大,当再生骨料取代率超过50%时,再生混凝土抗压强度下降速率逐渐减小,最终趋于稳定。由于凸型骨料内部较圆形骨料内部分布更多的离散裂缝,储存了更多的应变能,因此凸型骨料再生混凝土强度略高于普通混凝土。
4.4 网格尺寸的影响
基于势能原理的位移有限元法,在计算内部各点的位移时,需要构造单元的位移插值函数,位移插值函数虽然是连续的,但却是近似的。通过位移插值函数用有限自由度来描述具有无限自由度的体系,从而限制了单元的变形,其获得的位移近似解要小于精确解。同时,势能原理位移有限元的计算精度受到单元网格尺寸的影响,单元尺寸越小,位移的近似解越收敛于精确解。多数学者在进行混凝土材料的数值模拟时,单元尺寸通常选取为0.5$\sim$2.0 mm[14 -16 ,20 ,34 -35 ] 。为了研究基于基面力概念的势能有限元方法对网格尺寸的依赖性,本文借助凸型骨料模型研究有限元网格大小对计算结果的影响,试件尺寸为100 mm$\times$100 mm,以再生取代率为50%为例,单元网格尺寸由2.0 mm逐渐减小到0.5 mm,数值模拟结果如表4 所示。
由表4 可知,随着单元网格尺寸由2.0 mm逐渐降低至0.5 mm,抗压强度略微增加,但增幅较小,可以忽略。结果表明,单轴压缩载荷作用下,基于基面力元法的再生混凝土数值模拟对网格的依赖性较小。
5 结论
本文基于基面力概念及基面力元法,建立适用任意坐标系、任意形状的四边形单元势能基面力元模型,基于"瓦拉文公式"及"蒙特卡洛随机抽样算法"建立0%,30%,50%,70%及100%的二维圆形及任意凸多边形随机骨料模型,通过位移控制模式模拟单轴压缩试验,研究内部裂纹的萌生、扩展及基面力对单元网格尺寸的依赖性,结论如下:
(1)基于势能原理的基面力元法表达的刚度矩阵及节点位移具有显式的表达形式,求解过程中无需高斯积分且无精度损伤,具有精度高、计算速度快的优点。在数值模拟过程中,网格尺寸对数值模拟结果的影响可以忽略不计,表明基面力元模型对网格尺寸的依赖性较弱。
(2)单轴受压时内部微裂纹首先出现在新旧粘结带位置,裂纹较离散,随后贯穿新旧砂浆发展为斜向45$^\circ$连续破坏裂缝;再生骨料取代率较低时,试件内部形成1$\sim$2条斜向连续裂缝,随着再生骨料取代率的增加,斜向连续破坏裂缝数量增多、宽度增加并出现裂缝分叉现象,最终在骨料密集区域形成多条V型连续破坏裂缝。
(3)骨料形状对内部微裂纹发展路径影响较大,圆形骨料模型内部微裂纹沿切向方向发展为与骨料直径呈垂直状态的斜向连续裂缝;凸型骨料模型内部微裂纹沿骨料外轮廓线向骨料尖端发展为与骨料轮廓线呈平行状态的斜向连续裂缝,试件内部裂缝更离散。
(4)当再生骨料取代率较低时,再生混凝土的抗压强度下降速率较大,随着取代率的增加,抗压强度下降速率减小,最终趋于稳定。由于凸型骨料较圆形骨料能够吸收更多的应变能,因此凸型骨料再生混凝土强度略高于圆形骨料再生混凝土。
参考文献
View Option
[1]
Xiao JZ Li WG Fan H , et al . An overview of study on recycled aggregate concrete in China (1996-2011)
Construction and Building Materials 2012 ,31 :364 -383
DOI
URL
[本文引用: 2]
A series of investigations on the mechanical property, durability, and the structural performance of recycled aggregate concrete (RAC) have been carried out in the past 15 years (1996-2011) in China. The achievements of researches on recycled concrete are relatively sufficient to review and share with investigators from other countries. Some research progress of micro- and meso-structure of RAC is introduced in the first part of this paper. The second part of this paper is devoted to the mechanical properties of RAC material: strength, elastic modulus, Poisson's ratio, stress-strain curve. The third part of the paper gives research on durability of RAC: carbonization, chloride penetration, shrinkage and creep. The last part presents a review on the structural performance of RAC elements and structures: beams, columns, slabs, beam-column joints, shear walls as well as frames made with RAC. Results of all researches reveal that with proper design and construction, it is safe and feasible to apply RAC as a structural material in civil engineering. Moreover, in this paper, the relevant research results of RAC obtained in China and from other countries are compared and discussed. This review provides helpful directions to those who are already engaged in this research, and points out areas which are needed to promote safe and economic use of RAC. (C) 2011 Elsevier Ltd.
[2]
Wittmann FH Roelfstra PE Sadouki H . Simulation and analysis of composite structures
Materials Science & Engineering 1985 ,68 (2 ):239 -248
[本文引用: 2]
[3]
Liu C Liu HW Xiao JZ , et al . Effect of old mortar pore structure on relative humidity response of recycled aggregate concrete
Construction and Building Materials 2020 ,247 :118600
DOI
URL
[本文引用: 1]
[4]
王耀 , 赵华玮 , 胥民尧 等 . 基于基面力概念的二维凸多边形再生混凝土细观裂缝研究
混凝土 , 2018 ,349 (11 ):22 -26
Wang Yao Zhao Huawei Xu Minyao , et al . Research on meso-scopic cracks of 2-D convex polygon recycled aggregate concrete based on the concept of base force
Concrete 2018 ,349 (11 ):22 -26 (in Chinese)
[5]
杨子胜 , 刘盼 , 王文迪 等 . HRB400钢筋与钢纤维再生混凝土黏结性能及影响因素分析
混凝土与水泥制品 , 2020 (2 ):55 -59
Yang Zisheng Liu Pan Wang Wendi , et al . Analysis of bond performance and influencing factors between HRB400 steel and steel fiber recycled concrete
China Concrete and Cement Products 2020 ( 2 ):55 -59 (in Chinese)
[6]
Wang Y Peng YJ Kamel MA , et al . 2D numerical investigation on damage mechanism of recycled aggregate concrete prism
Construction and Building Materials 2019 ,213 :91 -99
DOI
URL
[本文引用: 1]
[7]
Bazant ZP Tabbara MR Kazemi MT , et al . Random particle models for fracture of aggregate or fiber composites
Asce Journal of Engineering Mechanics 1990 ,116 (8 ):1686 -1705
DOI
URL
[本文引用: 1]
[8]
Bažant ZP Byung HOH . Microplane model for progressive fracture of concrete and rock
Journal of Engineering Mechanics 1985 ,111 (4 ):559 -582
DOI
URL
[本文引用: 1]
[9]
Mohamed AR Hansen W . Micromechanical modeling of concrete response under static loading? Part 1: model development and validation
Aci Materials Journal 1999 ,96 (2 ):196 -203
[本文引用: 1]
[10]
Schlangen E Van Mier JG . Lattice model for numerical simulation of concrete fracture
International Conference on Dam Fracture, Denver, Colorado, USA , 1991
[本文引用: 1]
[11]
邢纪波 . 梁颗粒模型导论 . 北京 : 地震出版社 , 1999
[本文引用: 1]
[12]
Xiao JZ Li J Zhang C . Mechanical properties of recycled aggregate concrete under uniaxial loading
Cement & Concrete Research 2005 ,35 (6 ):1187 -1194
[本文引用: 1]
[13]
Xiao JZ Li WG Corr DJ , et al . Simulation study on the stress distribution in modeled recycled aggregate concrete under uniaxial compression
Journal of Materials in Civil Engineering 2013 ,25 (4 ):504 -518
DOI
URL
[本文引用: 4]
[14]
Jayasuriya A Adams MP Bandelt MJ . Understanding variability in recycled aggregate concrete mechanical properties through numerical simulation and statistical evaluation
Construction and Building Materials 2018 ,178 :301 -312
DOI
URL
[本文引用: 2]
[15]
Wang Y Zhao HW Xu MY , et al . Numerical studies on damage behavior of recycled aggregate concrete based on a 3D model
Materials 2020 ,13 :355 -369
DOI
URL
[本文引用: 1]
[16]
Peng YJ Liu YH . Application of base force element method to mesomechanics analysis for recycled aggregate concrete
Mathematical Problems in Engineering 2013 ,2013 :1 -8
[本文引用: 2]
[17]
Peng YJ Chu H Pu JW . Numerical simulation of recycled concrete using convex aggregate model and base force element method
Advances in Materials Science and Engineering 2016 ,2016 :1 -10
[本文引用: 1]
[18]
Gao YC . A new description of the stress state at a point with applications
Archive of Applied Mechanics 2003 ,73 (3 ):171 -183
DOI
URL
[本文引用: 1]
[19]
彭一江 . 基于基面力概念的新型有限元方法. [博士论文]
北京: 北京交通大学 , 2006
[本文引用: 1]
[20]
Wang Y Peng YJ Kamel MA , et al . Base force element method based on the complementary energy principle for the damage analysis of recycled aggregate concrete
International Journal for Numerical Methods in Engineering 2020 ,121 (7 ):1 -23
DOI
URL
[本文引用: 3]
[21]
Wang Y Peng YJ Kamel MA , et al . Modeling interfacial transition zone of RAC based on a degenerate element of BFEM
Construction and Building Materials 2020 ,252 :119063
DOI
URL
[本文引用: 1]
[22]
Walraven JC Reinhardt HW . Concrete mechanics. Part A: Theory and experiments on the mechanical behavior of cracks in plain and reinforced concrete subjected to shear loading. Nasasti/recon technical report n , 1981
[本文引用: 1]
[23]
Chen WF Plasticity in Reinforced Concrete . Plantation, FL : J Ross Publishing , 2007
[本文引用: 1]
[24]
Han DJ Chen WF . A nonuniform hardening plasticity model for concrete materials
Mechanics of Materials 1985 ,4 (34 ):283 -302
DOI
URL
[本文引用: 1]
[25]
Yoder PJ Iwan WD . On the formulation of strain-space plasticity with multiple loading surfaces
International Journal of Applied Mechanics 1981 ,48 (4 ):773 -778
[本文引用: 1]
[26]
Bazant ZP . Plastic fracturing theory for concrete
Journal of Engineering Mechanics 1979 ,105 (EM3 ):407 -428
[本文引用: 1]
[27]
Ottosen NS . Constitutive model for short-time loading of concrete
Journal of Engineering Mechanics 1979 ,105 (1 ):127 -141
[本文引用: 1]
[28]
Darwin D Pecknold DA . Nonlinear biaxial stress-strain law for concrete
Journal of Engineering Mechanics 1977 ,103 (2 ):229 -241
[本文引用: 1]
[29]
Thomas S Kurt HG . Simple formulation of concrete behavior under multiaxial load histories
Journal of the American Concrete 1985 ,82 (2 ):213221
[本文引用: 1]
[30]
过镇海 , 郭玉涛 , 徐焱 等 . 混凝土非线弹性正交异性本构模型
清华大学学报(自然科学版) , 1997 ,37 (6 ):80 -83
[本文引用: 1]
Guo Zhenhai Guo Yutao Xu Yan , et al . Nonlinear elastic orthotropic constitutive model for concrete
Journal of Tsinghua University (Sci & Tech) 1997 ,37 (6 ):80 -83 (in Chinese)
[本文引用: 1]
[31]
Lutz MP Monteiro PJM Zimmerman RW . Inhomogeneous interfacial transition zone model for the bulk modulus of mortar
Cement and Concrete Research 1997 ,27 :1113 -1122
DOI
URL
[本文引用: 2]
[32]
Mondal P Shah SP Marks LD . Nanomechanical properties of interfacial transition zone in concrete
Nanotechnology in Construction 2009 ,3 :3315 -3320
[33]
Li WG Luo ZY Sun ZH , et al . Numerical modelling of plastic--damage response and crack propagation in RAC under uniaxial loading
Magazine of Concrete Research 2018 ,70 (9 ):459 -472
DOI
URL
[本文引用: 2]
[34]
Du XL Jin L Ma GW . A meso-scale analysis method for the simulation of nonlinear damage and failure behavior of reinforced concrete members
International Journal of Damage Mechanics 2013 ,22 (6 ):878904
[本文引用: 1]
[35]
Tan X Li WG Zhao M , et al . Numerical discrete-element method investigation on failure process of recycled aggregate concrete
Journal of Materials in Civil Engineering 2019 ,31 (1 ):1 -14
[本文引用: 1]
An overview of study on recycled aggregate concrete in China (1996-2011)
2
2012
... 再生混凝土是利用再生骨料部分或全部替代天然骨料拌制的混凝土,可再次应用于建筑结构或者市政工程,实现资源的可持续利用,同时可有效解决废弃建筑垃圾造成的环境污染及资源浪费等问题,实现建筑垃圾的重复利用.虽然再生混凝土的力学性能低于普通混凝土,但研究证明,其仍然有应用于建筑结构的价值[1 ] . ...
... 基于断裂理论,材料力学研究分为宏观、细观、微观及纳观四个层次[2 ] .宏观层次上,再生混凝土的非均质性较普通混凝土更为复杂,通常被认为由再生粗骨料、新硬化水泥砂浆、老硬化水泥砂浆、老粘结带、新粘结带五相材料组成.各国学者对再生混凝土的基本力学性能或钢组合构件性能进行了大量研究,取得了丰富的成果[3 -6 ] .但由于材料来源不确定性、骨料形状及宏观试验环境等随机因素的影响,针对同一问题,不同学者基于不同试验目的结论离散程度较高[1 ] .基于细观层次理论的混凝土数值模拟方法,可以有效避免宏观试验各因素的不利影响,同时可弥补宏观试验时观察混凝土内部微裂纹开展及演变过程较为困难的不足,为混凝土等材料性能的研究提供了新思路. ...
Simulation and analysis of composite structures
2
1985
... 基于断裂理论,材料力学研究分为宏观、细观、微观及纳观四个层次[2 ] .宏观层次上,再生混凝土的非均质性较普通混凝土更为复杂,通常被认为由再生粗骨料、新硬化水泥砂浆、老硬化水泥砂浆、老粘结带、新粘结带五相材料组成.各国学者对再生混凝土的基本力学性能或钢组合构件性能进行了大量研究,取得了丰富的成果[3 -6 ] .但由于材料来源不确定性、骨料形状及宏观试验环境等随机因素的影响,针对同一问题,不同学者基于不同试验目的结论离散程度较高[1 ] .基于细观层次理论的混凝土数值模拟方法,可以有效避免宏观试验各因素的不利影响,同时可弥补宏观试验时观察混凝土内部微裂纹开展及演变过程较为困难的不足,为混凝土等材料性能的研究提供了新思路. ...
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
Effect of old mortar pore structure on relative humidity response of recycled aggregate concrete
1
2020
... 基于断裂理论,材料力学研究分为宏观、细观、微观及纳观四个层次[2 ] .宏观层次上,再生混凝土的非均质性较普通混凝土更为复杂,通常被认为由再生粗骨料、新硬化水泥砂浆、老硬化水泥砂浆、老粘结带、新粘结带五相材料组成.各国学者对再生混凝土的基本力学性能或钢组合构件性能进行了大量研究,取得了丰富的成果[3 -6 ] .但由于材料来源不确定性、骨料形状及宏观试验环境等随机因素的影响,针对同一问题,不同学者基于不同试验目的结论离散程度较高[1 ] .基于细观层次理论的混凝土数值模拟方法,可以有效避免宏观试验各因素的不利影响,同时可弥补宏观试验时观察混凝土内部微裂纹开展及演变过程较为困难的不足,为混凝土等材料性能的研究提供了新思路. ...
基于基面力概念的二维凸多边形再生混凝土细观裂缝研究
0
2018
基于基面力概念的二维凸多边形再生混凝土细观裂缝研究
0
2018
HRB400钢筋与钢纤维再生混凝土黏结性能及影响因素分析
0
2020
HRB400钢筋与钢纤维再生混凝土黏结性能及影响因素分析
0
2020
2D numerical investigation on damage mechanism of recycled aggregate concrete prism
1
2019
... 基于断裂理论,材料力学研究分为宏观、细观、微观及纳观四个层次[2 ] .宏观层次上,再生混凝土的非均质性较普通混凝土更为复杂,通常被认为由再生粗骨料、新硬化水泥砂浆、老硬化水泥砂浆、老粘结带、新粘结带五相材料组成.各国学者对再生混凝土的基本力学性能或钢组合构件性能进行了大量研究,取得了丰富的成果[3 -6 ] .但由于材料来源不确定性、骨料形状及宏观试验环境等随机因素的影响,针对同一问题,不同学者基于不同试验目的结论离散程度较高[1 ] .基于细观层次理论的混凝土数值模拟方法,可以有效避免宏观试验各因素的不利影响,同时可弥补宏观试验时观察混凝土内部微裂纹开展及演变过程较为困难的不足,为混凝土等材料性能的研究提供了新思路. ...
Random particle models for fracture of aggregate or fiber composites
1
1990
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
Microplane model for progressive fracture of concrete and rock
1
1985
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
Micromechanical modeling of concrete response under static loading? Part 1: model development and validation
1
1999
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
Lattice model for numerical simulation of concrete fracture
1
1991
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
1
1999
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
Mechanical properties of recycled aggregate concrete under uniaxial loading
1
2005
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
Simulation study on the stress distribution in modeled recycled aggregate concrete under uniaxial compression
4
2013
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
... 细观层次上,再生混凝土的结构特征可通过五相介质描述.因此,其力学性能受到五相介质基本力学参数的影响.Xiao等[13 ] 研究发现,骨料的弹性模量介于40$\sim$100 GPa,新砂浆及附着砂浆弹性模型介于17.5$\sim$40 GPa,新旧粘结带的弹性模量介于9.2$\sim$25.0 GPa.同时,试验表明[13 ,31 -33 ] ,新粘结带及旧粘结带的弹性模量为新砂浆及附着砂浆弹性模量的50%$\sim$80%.而粘结带作为骨料与砂浆之间的薄弱传力层,力学性能及粘结性能较差,因此本文取50%.结合文献[13 , 31 -33 ],本文数值模拟时,五相介质的力学参数取值如表2 所示. ...
... [13 ,31 -33 ],新粘结带及旧粘结带的弹性模量为新砂浆及附着砂浆弹性模量的50%$\sim$80%.而粘结带作为骨料与砂浆之间的薄弱传力层,力学性能及粘结性能较差,因此本文取50%.结合文献[13 , 31 -33 ],本文数值模拟时,五相介质的力学参数取值如表2 所示. ...
... ,新粘结带及旧粘结带的弹性模量为新砂浆及附着砂浆弹性模量的50%$\sim$80%.而粘结带作为骨料与砂浆之间的薄弱传力层,力学性能及粘结性能较差,因此本文取50%.结合文献[13 , 31 -33 ],本文数值模拟时,五相介质的力学参数取值如表2 所示. ...
Understanding variability in recycled aggregate concrete mechanical properties through numerical simulation and statistical evaluation
2
2018
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
... 基于势能原理的位移有限元法,在计算内部各点的位移时,需要构造单元的位移插值函数,位移插值函数虽然是连续的,但却是近似的.通过位移插值函数用有限自由度来描述具有无限自由度的体系,从而限制了单元的变形,其获得的位移近似解要小于精确解.同时,势能原理位移有限元的计算精度受到单元网格尺寸的影响,单元尺寸越小,位移的近似解越收敛于精确解.多数学者在进行混凝土材料的数值模拟时,单元尺寸通常选取为0.5$\sim$2.0 mm[14 -16 ,20 ,34 -35 ] .为了研究基于基面力概念的势能有限元方法对网格尺寸的依赖性,本文借助凸型骨料模型研究有限元网格大小对计算结果的影响,试件尺寸为100 mm$\times$100 mm,以再生取代率为50%为例,单元网格尺寸由2.0 mm逐渐减小到0.5 mm,数值模拟结果如表4 所示. ...
Numerical studies on damage behavior of recycled aggregate concrete based on a 3D model
1
2020
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
Application of base force element method to mesomechanics analysis for recycled aggregate concrete
2
2013
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
... 基于势能原理的位移有限元法,在计算内部各点的位移时,需要构造单元的位移插值函数,位移插值函数虽然是连续的,但却是近似的.通过位移插值函数用有限自由度来描述具有无限自由度的体系,从而限制了单元的变形,其获得的位移近似解要小于精确解.同时,势能原理位移有限元的计算精度受到单元网格尺寸的影响,单元尺寸越小,位移的近似解越收敛于精确解.多数学者在进行混凝土材料的数值模拟时,单元尺寸通常选取为0.5$\sim$2.0 mm[14 -16 ,20 ,34 -35 ] .为了研究基于基面力概念的势能有限元方法对网格尺寸的依赖性,本文借助凸型骨料模型研究有限元网格大小对计算结果的影响,试件尺寸为100 mm$\times$100 mm,以再生取代率为50%为例,单元网格尺寸由2.0 mm逐渐减小到0.5 mm,数值模拟结果如表4 所示. ...
Numerical simulation of recycled concrete using convex aggregate model and base force element method
1
2016
... 基于数值混凝土的概念[2 ] ,细观模型的提出及发展为混凝土力学性能的数值模拟研究提供了理论基础,较成熟的有随机颗粒模型[7 ] 、微平面模型[8 ] 、微观模型[9 ] 、格点模型[10 ] 及束粒子模型[11 ] .Xiao等[12 -13 ] 通过规则分布的圆形骨料模型研究再生混凝土材料的力学性能.研究发现内部微裂纹首先出现在粘结带区域,且粘结带区域存在拉伸应力及剪切应力集中现象,并研究了各项材料对应力集中程度的影响.Jayasuriya等[14 ] 通过建立老砂浆含量为2%,10%,20%及50%的细观数值模型,研究老砂浆含量对再生混凝土力学性能的研究.数值模拟结果表明随着老砂浆含量的递增,再生混凝土弹性模量及抗压强度逐渐递减,而极限压应变逐渐递增.Wang等[15 ] 和Peng等[16 -17 ] 通过再生骨料含量100%的圆形随机骨料模型研究了再生混凝土的单轴拉伸强度及单轴压缩强度.研究表明再生混凝土的强度低于普通混凝土,且内部微裂纹首先出现在老粘结带. ...
A new description of the stress state at a point with applications
1
2003
... 本文基于势能原理的基面力元法[18 -19 ] ,以单元边界长度与单元的外法向量的乘积为基本元素,通过利用连续介质学理论推导四边形单元应变及刚度矩阵显式表达式,可解决ANSYS,ABAQUS等常规有限元软件需要构造位移插值函数及借助高斯积分才能求解刚度矩阵等限制,适用于任意坐标系任意平面及空间单元静力及动力分析[20 -21 ] . ...
基于基面力概念的新型有限元方法. [博士论文]
1
2006
... 本文基于势能原理的基面力元法[18 -19 ] ,以单元边界长度与单元的外法向量的乘积为基本元素,通过利用连续介质学理论推导四边形单元应变及刚度矩阵显式表达式,可解决ANSYS,ABAQUS等常规有限元软件需要构造位移插值函数及借助高斯积分才能求解刚度矩阵等限制,适用于任意坐标系任意平面及空间单元静力及动力分析[20 -21 ] . ...
Base force element method based on the complementary energy principle for the damage analysis of recycled aggregate concrete
3
2020
... 本文基于势能原理的基面力元法[18 -19 ] ,以单元边界长度与单元的外法向量的乘积为基本元素,通过利用连续介质学理论推导四边形单元应变及刚度矩阵显式表达式,可解决ANSYS,ABAQUS等常规有限元软件需要构造位移插值函数及借助高斯积分才能求解刚度矩阵等限制,适用于任意坐标系任意平面及空间单元静力及动力分析[20 -21 ] . ...
... 细观数值模拟过程中,材料的损伤本构模型对材料的载荷响应行为具有重要的影响.作为非均质复合材料,没有统一且特定的损伤本构模型来描述再生混凝土在载荷作用下的损伤行为.基于试验及理论研究,弹塑性模型[23 ] 、非均匀强化塑性模型[24 ] 、塑性模型[25 ] 、塑性断裂模型[26 ] 、Ottosen模型[27 ] 、Darwin-Pecknold模型[28 ] 、Stankow-Gerstle模型[29 ] 及过-徐模型[30 ] 等一系列数学模型被提出以描述混凝土的细观力学行为.本文基于最大拉应力强度准则,通过多折线损伤模型[20 ] 表征五相介质在位移载荷作用下的力学行为,如图8 所示. ...
... 基于势能原理的位移有限元法,在计算内部各点的位移时,需要构造单元的位移插值函数,位移插值函数虽然是连续的,但却是近似的.通过位移插值函数用有限自由度来描述具有无限自由度的体系,从而限制了单元的变形,其获得的位移近似解要小于精确解.同时,势能原理位移有限元的计算精度受到单元网格尺寸的影响,单元尺寸越小,位移的近似解越收敛于精确解.多数学者在进行混凝土材料的数值模拟时,单元尺寸通常选取为0.5$\sim$2.0 mm[14 -16 ,20 ,34 -35 ] .为了研究基于基面力概念的势能有限元方法对网格尺寸的依赖性,本文借助凸型骨料模型研究有限元网格大小对计算结果的影响,试件尺寸为100 mm$\times$100 mm,以再生取代率为50%为例,单元网格尺寸由2.0 mm逐渐减小到0.5 mm,数值模拟结果如表4 所示. ...
Modeling interfacial transition zone of RAC based on a degenerate element of BFEM
1
2020
... 本文基于势能原理的基面力元法[18 -19 ] ,以单元边界长度与单元的外法向量的乘积为基本元素,通过利用连续介质学理论推导四边形单元应变及刚度矩阵显式表达式,可解决ANSYS,ABAQUS等常规有限元软件需要构造位移插值函数及借助高斯积分才能求解刚度矩阵等限制,适用于任意坐标系任意平面及空间单元静力及动力分析[20 -21 ] . ...
1
1981
... 根据瓦拉文公式[22 ] ,试件内骨料粒径$D<D_{0} $的累积分布概率为 ...
1
2007
... 细观数值模拟过程中,材料的损伤本构模型对材料的载荷响应行为具有重要的影响.作为非均质复合材料,没有统一且特定的损伤本构模型来描述再生混凝土在载荷作用下的损伤行为.基于试验及理论研究,弹塑性模型[23 ] 、非均匀强化塑性模型[24 ] 、塑性模型[25 ] 、塑性断裂模型[26 ] 、Ottosen模型[27 ] 、Darwin-Pecknold模型[28 ] 、Stankow-Gerstle模型[29 ] 及过-徐模型[30 ] 等一系列数学模型被提出以描述混凝土的细观力学行为.本文基于最大拉应力强度准则,通过多折线损伤模型[20 ] 表征五相介质在位移载荷作用下的力学行为,如图8 所示. ...
A nonuniform hardening plasticity model for concrete materials
1
1985
... 细观数值模拟过程中,材料的损伤本构模型对材料的载荷响应行为具有重要的影响.作为非均质复合材料,没有统一且特定的损伤本构模型来描述再生混凝土在载荷作用下的损伤行为.基于试验及理论研究,弹塑性模型[23 ] 、非均匀强化塑性模型[24 ] 、塑性模型[25 ] 、塑性断裂模型[26 ] 、Ottosen模型[27 ] 、Darwin-Pecknold模型[28 ] 、Stankow-Gerstle模型[29 ] 及过-徐模型[30 ] 等一系列数学模型被提出以描述混凝土的细观力学行为.本文基于最大拉应力强度准则,通过多折线损伤模型[20 ] 表征五相介质在位移载荷作用下的力学行为,如图8 所示. ...
On the formulation of strain-space plasticity with multiple loading surfaces
1
1981
... 细观数值模拟过程中,材料的损伤本构模型对材料的载荷响应行为具有重要的影响.作为非均质复合材料,没有统一且特定的损伤本构模型来描述再生混凝土在载荷作用下的损伤行为.基于试验及理论研究,弹塑性模型[23 ] 、非均匀强化塑性模型[24 ] 、塑性模型[25 ] 、塑性断裂模型[26 ] 、Ottosen模型[27 ] 、Darwin-Pecknold模型[28 ] 、Stankow-Gerstle模型[29 ] 及过-徐模型[30 ] 等一系列数学模型被提出以描述混凝土的细观力学行为.本文基于最大拉应力强度准则,通过多折线损伤模型[20 ] 表征五相介质在位移载荷作用下的力学行为,如图8 所示. ...
Plastic fracturing theory for concrete
1
1979
... 细观数值模拟过程中,材料的损伤本构模型对材料的载荷响应行为具有重要的影响.作为非均质复合材料,没有统一且特定的损伤本构模型来描述再生混凝土在载荷作用下的损伤行为.基于试验及理论研究,弹塑性模型[23 ] 、非均匀强化塑性模型[24 ] 、塑性模型[25 ] 、塑性断裂模型[26 ] 、Ottosen模型[27 ] 、Darwin-Pecknold模型[28 ] 、Stankow-Gerstle模型[29 ] 及过-徐模型[30 ] 等一系列数学模型被提出以描述混凝土的细观力学行为.本文基于最大拉应力强度准则,通过多折线损伤模型[20 ] 表征五相介质在位移载荷作用下的力学行为,如图8 所示. ...
Constitutive model for short-time loading of concrete
1
1979
... 细观数值模拟过程中,材料的损伤本构模型对材料的载荷响应行为具有重要的影响.作为非均质复合材料,没有统一且特定的损伤本构模型来描述再生混凝土在载荷作用下的损伤行为.基于试验及理论研究,弹塑性模型[23 ] 、非均匀强化塑性模型[24 ] 、塑性模型[25 ] 、塑性断裂模型[26 ] 、Ottosen模型[27 ] 、Darwin-Pecknold模型[28 ] 、Stankow-Gerstle模型[29 ] 及过-徐模型[30 ] 等一系列数学模型被提出以描述混凝土的细观力学行为.本文基于最大拉应力强度准则,通过多折线损伤模型[20 ] 表征五相介质在位移载荷作用下的力学行为,如图8 所示. ...
Nonlinear biaxial stress-strain law for concrete
1
1977
... 细观数值模拟过程中,材料的损伤本构模型对材料的载荷响应行为具有重要的影响.作为非均质复合材料,没有统一且特定的损伤本构模型来描述再生混凝土在载荷作用下的损伤行为.基于试验及理论研究,弹塑性模型[23 ] 、非均匀强化塑性模型[24 ] 、塑性模型[25 ] 、塑性断裂模型[26 ] 、Ottosen模型[27 ] 、Darwin-Pecknold模型[28 ] 、Stankow-Gerstle模型[29 ] 及过-徐模型[30 ] 等一系列数学模型被提出以描述混凝土的细观力学行为.本文基于最大拉应力强度准则,通过多折线损伤模型[20 ] 表征五相介质在位移载荷作用下的力学行为,如图8 所示. ...
Simple formulation of concrete behavior under multiaxial load histories
1
1985
... 细观数值模拟过程中,材料的损伤本构模型对材料的载荷响应行为具有重要的影响.作为非均质复合材料,没有统一且特定的损伤本构模型来描述再生混凝土在载荷作用下的损伤行为.基于试验及理论研究,弹塑性模型[23 ] 、非均匀强化塑性模型[24 ] 、塑性模型[25 ] 、塑性断裂模型[26 ] 、Ottosen模型[27 ] 、Darwin-Pecknold模型[28 ] 、Stankow-Gerstle模型[29 ] 及过-徐模型[30 ] 等一系列数学模型被提出以描述混凝土的细观力学行为.本文基于最大拉应力强度准则,通过多折线损伤模型[20 ] 表征五相介质在位移载荷作用下的力学行为,如图8 所示. ...
混凝土非线弹性正交异性本构模型
1
1997
... 细观数值模拟过程中,材料的损伤本构模型对材料的载荷响应行为具有重要的影响.作为非均质复合材料,没有统一且特定的损伤本构模型来描述再生混凝土在载荷作用下的损伤行为.基于试验及理论研究,弹塑性模型[23 ] 、非均匀强化塑性模型[24 ] 、塑性模型[25 ] 、塑性断裂模型[26 ] 、Ottosen模型[27 ] 、Darwin-Pecknold模型[28 ] 、Stankow-Gerstle模型[29 ] 及过-徐模型[30 ] 等一系列数学模型被提出以描述混凝土的细观力学行为.本文基于最大拉应力强度准则,通过多折线损伤模型[20 ] 表征五相介质在位移载荷作用下的力学行为,如图8 所示. ...
混凝土非线弹性正交异性本构模型
1
1997
... 细观数值模拟过程中,材料的损伤本构模型对材料的载荷响应行为具有重要的影响.作为非均质复合材料,没有统一且特定的损伤本构模型来描述再生混凝土在载荷作用下的损伤行为.基于试验及理论研究,弹塑性模型[23 ] 、非均匀强化塑性模型[24 ] 、塑性模型[25 ] 、塑性断裂模型[26 ] 、Ottosen模型[27 ] 、Darwin-Pecknold模型[28 ] 、Stankow-Gerstle模型[29 ] 及过-徐模型[30 ] 等一系列数学模型被提出以描述混凝土的细观力学行为.本文基于最大拉应力强度准则,通过多折线损伤模型[20 ] 表征五相介质在位移载荷作用下的力学行为,如图8 所示. ...
Inhomogeneous interfacial transition zone model for the bulk modulus of mortar
2
1997
... 细观层次上,再生混凝土的结构特征可通过五相介质描述.因此,其力学性能受到五相介质基本力学参数的影响.Xiao等[13 ] 研究发现,骨料的弹性模量介于40$\sim$100 GPa,新砂浆及附着砂浆弹性模型介于17.5$\sim$40 GPa,新旧粘结带的弹性模量介于9.2$\sim$25.0 GPa.同时,试验表明[13 ,31 -33 ] ,新粘结带及旧粘结带的弹性模量为新砂浆及附着砂浆弹性模量的50%$\sim$80%.而粘结带作为骨料与砂浆之间的薄弱传力层,力学性能及粘结性能较差,因此本文取50%.结合文献[13 , 31 -33 ],本文数值模拟时,五相介质的力学参数取值如表2 所示. ...
... , 31 -33 ],本文数值模拟时,五相介质的力学参数取值如表2 所示. ...
Nanomechanical properties of interfacial transition zone in concrete
0
2009
Numerical modelling of plastic--damage response and crack propagation in RAC under uniaxial loading
2
2018
... 细观层次上,再生混凝土的结构特征可通过五相介质描述.因此,其力学性能受到五相介质基本力学参数的影响.Xiao等[13 ] 研究发现,骨料的弹性模量介于40$\sim$100 GPa,新砂浆及附着砂浆弹性模型介于17.5$\sim$40 GPa,新旧粘结带的弹性模量介于9.2$\sim$25.0 GPa.同时,试验表明[13 ,31 -33 ] ,新粘结带及旧粘结带的弹性模量为新砂浆及附着砂浆弹性模量的50%$\sim$80%.而粘结带作为骨料与砂浆之间的薄弱传力层,力学性能及粘结性能较差,因此本文取50%.结合文献[13 , 31 -33 ],本文数值模拟时,五相介质的力学参数取值如表2 所示. ...
... -33 ],本文数值模拟时,五相介质的力学参数取值如表2 所示. ...
A meso-scale analysis method for the simulation of nonlinear damage and failure behavior of reinforced concrete members
1
2013
... 基于势能原理的位移有限元法,在计算内部各点的位移时,需要构造单元的位移插值函数,位移插值函数虽然是连续的,但却是近似的.通过位移插值函数用有限自由度来描述具有无限自由度的体系,从而限制了单元的变形,其获得的位移近似解要小于精确解.同时,势能原理位移有限元的计算精度受到单元网格尺寸的影响,单元尺寸越小,位移的近似解越收敛于精确解.多数学者在进行混凝土材料的数值模拟时,单元尺寸通常选取为0.5$\sim$2.0 mm[14 -16 ,20 ,34 -35 ] .为了研究基于基面力概念的势能有限元方法对网格尺寸的依赖性,本文借助凸型骨料模型研究有限元网格大小对计算结果的影响,试件尺寸为100 mm$\times$100 mm,以再生取代率为50%为例,单元网格尺寸由2.0 mm逐渐减小到0.5 mm,数值模拟结果如表4 所示. ...
Numerical discrete-element method investigation on failure process of recycled aggregate concrete
1
2019
... 基于势能原理的位移有限元法,在计算内部各点的位移时,需要构造单元的位移插值函数,位移插值函数虽然是连续的,但却是近似的.通过位移插值函数用有限自由度来描述具有无限自由度的体系,从而限制了单元的变形,其获得的位移近似解要小于精确解.同时,势能原理位移有限元的计算精度受到单元网格尺寸的影响,单元尺寸越小,位移的近似解越收敛于精确解.多数学者在进行混凝土材料的数值模拟时,单元尺寸通常选取为0.5$\sim$2.0 mm[14 -16 ,20 ,34 -35 ] .为了研究基于基面力概念的势能有限元方法对网格尺寸的依赖性,本文借助凸型骨料模型研究有限元网格大小对计算结果的影响,试件尺寸为100 mm$\times$100 mm,以再生取代率为50%为例,单元网格尺寸由2.0 mm逐渐减小到0.5 mm,数值模拟结果如表4 所示. ...