最近在微信群中有人提出物理中的"力"是否与力学中"力"的概念不一样的问题。我们一些朋友在家工作,通过网络对力的定义、测量和作用等共同感兴趣的几个问题作了一番云中群聊。

习: 我们当力学教师的几乎每堂课都会提到"力",每个课题都会用到"力",但是"力"这个词粗看起来很熟悉,细琢磨起来往往还感到有几分模糊。的确,大百科全书中已经给出了一个简洁和准确的定义:力是物质间的一种相互作用,机械运动状态变化是由这种相互作用引起的^[1]。但是,有些问题就连"力学圈"的人也不一定每人都能立即说得很清楚。我们能不能在云里聊聊与力有关的几个基础性的"傻瓜"问题?

姜: 好啊！先说说"圈外人"怎么看力?这里所说的所谓"圈外人"是指行走在城市大街上、农村乡间小路上没有受到相关力学熏陶的普通人。据我们感知,他们一般不感兴趣所谓"力"的定义,但知道有"力"这个词的存在。他们会从一个人的力气大小、大树被大风刮倒、物体的轻重、汽车的载重量和速度、一个物体被另一个物体砸坏等日常生活现象中感受力的存在和力的大小。在桥上没有车辆和行人时,他们一般不会觉察到悬索桥上的悬索中力的存在。他们会用秤去称重物,但一般不去考虑杠杆原理;他们会带弹簧秤去买菜,但一般不去考虑弹簧材料的本构关系,更不会考虑标定问题。

周: 力是表征物体之间相互作用程度的物理量,它的量值通过它产生的效果,即造成物体发生运动状态或形状的改变来确定。

姜: 我认为上述论述中的"相互作用"限定为"相互间的机械作用"更合理一些,以区别于电磁感应、化学反应等相互作用。

习: 或者说,力是使物质(气、液、固)形态(包含形状和姿态)发生变化的一种作用。

余: 定性来说,力是表征物体之间相互作用程度的物理量,在牛顿力学中它是一个矢量,具有大小、方向和作用点(线)三个要素。

定量来说,牛顿首先把"力"定义为动量随时间的变化率,即

式中 ${F}$ 为研究对象所受到的合力,$m$为研究对象的质量,${v}$为研究对象的速度。

姜: 在质量恒定的前提下,式(1)可改写为

式中 ${a} $为研究对象的加速度,这也正是牛顿第二定律的现代通用形式。《中国大百科全书$\cdot$力学》中论及力的概念时,也这样定义:"力是使物体获得加速度或形变的外因。在动力学中它等于物体的质量与加速度的乘积。"^[1]

周: 值得说明的是,经查阅文献可以发现牛顿最早所说的"运动(motion)"和"力(force)"是现代意义下的动量和冲量。这从他的著作原文^[2]可以看出(图1)。"界说二:凡动之几何为速与质相乘数"、"公论二:凡动之变与所加之力有比例亦准加力之方向"(李善兰《奈端数理》译语)。可以说牛顿的"牛顿第二定律"其实是冲量定理。但是,牛顿在论著中思考的都是一个微小的恒定时间间隔下的变化量,现代版的牛顿第二定律,即上述式(1)和式(2),依然是牛顿动力学思想的忠实表达。

余: 与牛顿同时代的莱布尼兹出于形而上的哲学思考,也提出过力的另一种概念,有些概念从物理学上似乎更加本质^[3]。例如,莱布尼兹提出过"活力(vis viva)"理论,把$mv^{2}$称为"活力",认为应该用它而不是用动量来度量力^[4]。经过对"活力"进行修正之后,力学家们同意,力也可以定义为动能对位移的微商,即

式中 ${s}$ 为研究对象的位移。

显然,式(1)$\sim$式(3)都可以被当作力的定义,这些定义把力同几个基本物理量($m, v, t, s$)联系起来了。

习: 牛顿将力定义为动量随时间的变化率,而莱布尼兹将力定义为动能随位移的变化率。初学者可能会问到底谁的定义对呢?这两种定义之间有什么异同点吗?

余: 这两个定义分别从不同角度定义了力。从本质上讲,这两种定义是完全等同的。从牛顿对力的定义式可以导出莱布尼兹对力的定义式

因而,两种定义都是正确的,定义的是同一个力,只是参照的物理量不同。我们常用的还是牛顿关于力的定义,即式(1)或式(2)。事实上,如果我们将牛顿第二定律式(2)两边对时间积分,便可得到动量定理;而如果将该定律两边对位移积分,便可得到动能定理。

习: 这样说来,只有在动力学的意义下才能真正地定义力是什么。而我们在教理论力学课程的时候通常是按照"静力学、运动学、动力学"这样一个顺序来教。在没有教动力学之前,我们在静力学部分应该怎样解释力呢?

余: 从历史上来看,人类对于"力"的概念始自于自己在做推、拉、提、举、扛等动作时肌肉的紧张程度,然后推广至牛、马等服役家畜的干活能力的评估。可以说,"力" 最先来自人自身肌肉的感受。静力学解释了力的分解、合成及平衡,实际上讲的是矢量数学的规律,没牵涉到力的本身;而对力本身的理解,也只能停留在自身肌肉的感受,以及对物体重量的感知。在静力学范畴内是无法给出力的定义的。

姜: 力具有$MLT^{-2}$的量纲,它是根据${F}=m{a}$,由质量、长度、时间的基本量纲$M$、$L$、$T$导出的量纲。质量、长度、时间这三个量都是可以直接度量的基本量,它们有国际公认的基准,即千克、米、秒。力只是一个导出量,而不是基本量。我们这里对"力"的量纲的理解直接支持上述论断,即:"力只能在动力学意义下定义"。

习: 那么,力可以用什么方法测量呢?是不是先要对"力"进行标定呢?

姜: 标定"力"的意思是标定力传感器。关键在于如何知道作用在一个具体传感器上的标准的力,即精确的"力"。这种标定所需的物理量必须是已知的或精确可测的。由于力的定义来自牛顿第二定律,只能通过牛顿第二定律(在物体运动速度远低于光速和它的几何尺度远大于量子几何尺度的条件下,它可以被认为是自然界物体运动规律的正确表述)来测得这样的标准力。具体方法可以分为两步:

第一步:测量当地的重力加速度$g$

最简单的重力加速度测定是直接度量落体在给定时间内下落的距离。为了获得更精细读数,1784年,G.阿脱伍德将质量同为$M$的重块用轻质细绳连接后,跨在光滑的轻质滑轮上,再在一个重块上附加一重量小得多的重块$m$ (如图2所示)^[5]。这时,重力拖动大质量物块,使其产生一微小加速度$a={mg}/({2M+m})$。测得$a$后,即可算出$g$。

第二步:测量作用在一个弹性体上的力

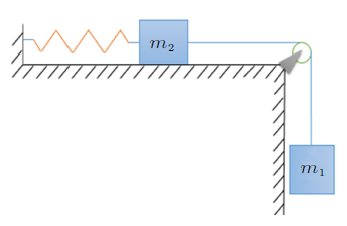
在一光滑平台的最左端固定一个轻质弹性体(如轻质弹簧),弹性体的右端与一放置在光滑平台上的质量块$m_{2}$相连,质量块$m_{2}$的右侧经过轻质细绳跨过平台边缘的轻质滑轮与另一质量块$m_{1}$相连,如图3所示。在重力$m_{1}g$的作用下,测得质量块$m_{2}$和$m_{1}$的共同加速度$a$,可以得到弹性体作用于质量块$m_{2}$的力的大小。从而完成了对力传感器(弹簧)的标定与力的精确测量。

周: 同意上面的原理性描述,"力"的定义来自牛顿第二定律,力的标定只能通过这个定律进行。由于人们对力的直接感觉往往来自于重力,只要标定了重力加速度,就可以通过物体(如砝码)质量来标定力。从另一个角度来看,既然"重力 = 质量 $\times$ 重力加速度",也可以利用单摆或者其他重力摆的振动频率来测量重力加速度。

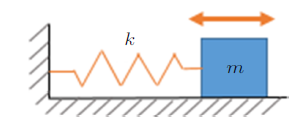
常见的测量力的方法是通过测量固体的变形(利用胡克定律)来进行。胡克说过 "ut tensio, sic vis (the extension is proportional to the force)" ("伸长与力成正比"),把力$F$和变形$x$直接联系起来了:$F=kx$。力导致固体(如弹簧)发生形变,如果已知弹簧的弹性常数$k$,根据测量弹簧的拉伸量,就可以计算出$F$。但是,如何去确定$k$?一般人可能会想到中学实验,用砝码和直尺来标定它的弹性常数——这个实验的隐含条件是砝码的重力是先验确定的。其实,我们可以绕过"已知力"的假设,只要将轻质弹簧与一个已知质量块$m$连接,形成一个"弹簧-质量块"系统(图4),其振动圆频率$\omega=\sqrt{k/m}$,通过测出这个系统的振动周期$T=2\pi /\omega$,就可以很方便地确定弹簧的弹性常数

姜: 前面基于动力学原理获得了标准"力",也完成了力传感器的标定与对力的精确测量,比如图3和图4弹簧刚度标定和弹簧力的测量。在力已标定的基础上,或者说,在材料本构已知的前提下,从力的效果考虑,在一个平衡系统中,便可以通过测量固体的变形从而测量出产生该变形的力,例如弹簧秤和应变片都基于这个原理。力还具有其他表观的物理效果,如肌电、压电、压磁、压阻、压力相变、压力发光(triboluminescence)等,利用这些原理也能够构筑新的传感器和测试系统。对相应传感器进行标定后,被用来进行广泛的、工程意义上的力的测量。

目前只能用"运动状态改变"来进行本源意义上的力的测量,因为这种测量所用到的物理量都有相应的国际标准。利用任何一个经过"标准力"标定的变形、压电等类型的力传感器都可在实验室和工程中进行力的测量。

周: 上面的讨论很有意义,牛顿第二定律给出了"力"的动力学定义,也给出了力的测量方法,从而形成完整的逻辑关联。在这里我想强调一下胡克定律在"测力"过程中也具有动力学意义:早期通过变形(肌肉紧张等)来理解力,是"静力学"的概念;但是胡克定律在动力学系统中依旧有效。不必借助其他的"高阶(更加敏感)"的力传感器,直接采用动力学方法,也能标定弹性元件的弹性系数,如图4和式(5)所示,通过振动系统的周期可以标定弹簧的"弹性系数"。

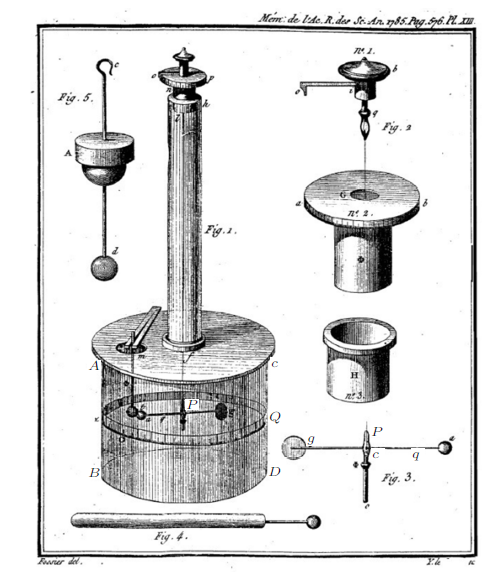
历史上,采用这种方法测量力,解决了许多重要物理问题。例如:在著名的卡文迪许实验^[6]中,通过测量悬吊金属丝的扭转角度,乘以其扭转刚度,来测量质量之间引力的大小(图5);同样,库伦也利用扭杆(图6)测量了带电球体间的相互作用力、进而研究静电力随空间距离的变化关系^[7]。在这些著名实验中,卡文迪许的悬吊金属丝^[6]、以及库伦的扭杆^[7-8]的"扭转刚度"都是通过测量扭摆振动周期,再利用系统的转动惯量而换算出来的,其换算公式类似于式(5)。这表明,扭摆这样的精密测力系统,其测量基础也是牛顿动力学。库伦和卡文迪许正是通过这些精确的力测量,给出了电荷量的测量基准、以及地球质量和万有引力常数等基本物理数据。

习: 把改变物体运动状态的"力"同产生物体变形的"力"统一起来以后,我们是不是可以说在牛顿力学中,"力"只有一种,但表现形式有很多种呢?

周: 在牛顿力学的范畴内,"力"只有一种,即前面所定义的相互作用的量。力本身源于牛顿第二定律$F=ma$,而在胡克定律$F=kx$,或者万有引力公式$F=Gm_{1}m_{2}/r^{2}$之中所见到的$F$同样都是这个力。造成运动状态变化的相互作用、物质之间或者内部的电磁力作用、或者物质之间的万有引力作用,在物理上的效果都是一样的。

余: 除万有引力(包括重力)和电磁力外,牛顿力学中大量处理的是表面力。比如,虽然不容易观察到空气与物体的接触,但空气中传播的冲击波对物体的作用显然也是一种表面的接触力。

姜: 如果跳出牛顿力学讨论"力"的分类,自然界所有的基本力可以分为四个基本类,即:强相互作用力、弱相互作用力、电磁(相互作用)力、万有引力。

周: 我的理解是,现代物理学中"力"代表物质世界的自然的相互作用,根据具体的物理本质,分为两种长程相互作用(即质量之间的万有引力、电荷之间的电磁力)和两种亚原子核尺度的短程相互作用(即夸克之间的强相互作用和弱相互作用)。物理学关注力的本源,即相互作用本源的探讨。如现代物理学已经证实两种长程相互作用的等价性;而经典力学(即牛顿力学)则主要讨论这两种长程相互作用力的作用效果。

余: 我认为,"物理中的力"和"力学中的力"之所以概念有所不同,除了物理学着重于机理与本源、力学着重于运动状态与变形等效果这个基本的学科特性的差异之外,也在于物理学研究的物质尺度(微观,以$\mu$m为量级)同经典力学研究的尺度(宏观,以mm和m为量级)有着重大差异。

习: 近几十年来由于微尺度力学、纳米力学、物理力学和分子动力学的兴起,物理中的"力"和力学中的"力"之间的上述差异是否在逐渐弥合之中?

姜: 我不认为两者在弥合。在二十世纪之前,科学界普遍认为牛顿力学的定律在自然界具有普适性。在相对论和量子力学得到科学界认可后,牛顿力学的定律在物体的运动速度接近光速和所研究粒子的几何尺度接近量子几何尺度的情况下不再适用,相应的"力"的概念也不再相同,因此物理中的"力"和力学中的"力"之间的差异并没有"弥合"之意,界线本来就是清楚的。在我们的研究对象没有跨入量子范畴之前(即:研究对象的轨迹还是可确定的),牛顿力学与物理中的力学没有本质区别,所以牛顿力学原理对细观力学、微尺度力学、纳米力学都是有用的。当我们的研究对象的尺度与量子同量级(或相近)时,相应作用规律应当用量子力学去研究。需要强调的是,"量子力学"的"力学"只是沿用了"力学"这个词而已,与我们常规讨论的牛顿力学中的"力学"已经没有多少关系。有点像"对物体的作用力"与社会学中"生产力" 之间的关系,只是使用的"力"字在表面相同而已。

周: 现代物理学认为力只是相互作用的定量表征,因此追究其本源,即相互作用势$U\left({r} \right)$,力作为势能的空间导数${F}=-{\partial U}/{\partial{r}}$,是一个导出量^[9]。在力学或者工程学中,力则是一个具有清晰定义、可量测、可计算的本质物理量。由于引入"力"的量,加之有关连续性的一些假设,物质之间的相互作用、运动、变形等问题能够在一个相当清晰和优雅的数学分析框架中进行分解、分析和计算;有了描述固体、流体、流变体等介质的"力学"模型,并因此而积累的大量描述具体材料的变形、损伤、破坏等与力相关的数据库,形成了各种力学分析和计算软件、建立了工程结构的性能和安全性分析的规范和标准。可以说,"力"以及据此建立的力学是现代工业发展和人类文明进步的不可缺少的一个学科体系。

网友: (北京航空航天大学殷莎)随着交叉力学的发展,比如在多尺度多物理场耦合问题中,力学人也开始关注物理本质,因此是否可以说传统力学与物理之间在力学概念和研究内涵上差别越来越小?另外,在新的交叉学科中如与化学、生物医学、信息学、人机交互中,力的概念在本质上有没有改变呢?

姜: 殷莎和习会峰老师的问题带有普遍性,从另一个角度也反映我们这次云聊的意义。基于人类的基本生存需要,力学和天文学是发展最早的科学,可以说它们是科学的始祖。后来天文学的好多课题都成了力学的研究内容。力学为后来的科学提供了许多重要的思想和方法。随着力学研究工作在多个领域的深入开展,出现了所谓的"交叉力学"。我个人认为所谓"交叉"其实是"深入和应用"。我们这里讨论的是有"力"的力学,对它我是这样理解的:研究在牛顿力学中定义的力的作用下,作用过程满足质量守恒、动量守恒、能量守恒方程,涉及连续介质时还遵循相应的本构方程的研究对象的运动、变形和破坏规律的科学。所谓微尺度力学、纳米力学和混凝土力学等等只是上述有"力"的力学的思想和方法在某个尺度上或以某个材料为主的研究对象中的深入、具体的应用。因而大多数所谓"交叉力学"都仍然没有脱离牛顿力学的框架,都满足四类基本方程。另一方面,随着力学的术语为大众所熟悉,逐步渗透到其他学科,也出现了许多"没有力"的"XX力学",但这已经不在我们讨论的范畴之内了。

习: 通过这次云中群聊,对"力"的概念、力的测量及力学的重要地位真是越聊越明白了呢！

余: 确实如此,我们这样的云聊可以互相启发、集思广益,同时对于有争议的问题,也能够各抒已见、求同存异。比如说,在这次云聊中我们找到了为什么力学教师在静力学部分总是讲不清楚"力"到底是什么的原因,这就是,只有在动力学中才能真正给出力的定义。我们也谈到了牛顿第二定律定义的力与莱布尼兹从能量角度诠释的力的一致性。再比如,我们可以通过观测受力物体的运动状态改变来标定力,也可以利用力所产生的物体运动或变形的周期、频率来标定力;而一旦建立起了力的基准,根据胡克定律就可以利用固体(例如弹簧或传感器)的变形相当便捷地测定科学实验和工程中的力的量值。

力学的教学和研究中还有一些大家都关心的共同话题,也许下次我们还可以继续云聊。