滑块碰撞是牛顿力学中常见的问题,一般通过动量守恒和能量变化的关系去研究碰撞过程;而圆周率$\pi$是几何数学的问题,为圆的周长与直径之比,历史上我国数学家刘徽通过割圆术算出$\pi$的小数点后第5位3.14159,之后数学家们计算出的小数点后位数越来越多[1 -2 ] 。$\pi$的数字为:3.14159265358979323846264338327950288419716939937510$\cdots$,滑块碰撞与 这两者看起来毫无联系,但有趣的是,作者在研究碰撞问题时,发现滑块的碰撞次数与$\pi$极其相似,并分析了它们的内在关联。
1 问题来源
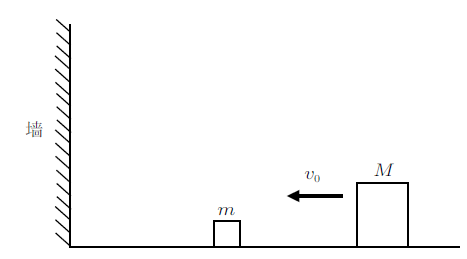
如图1 所示,水平光滑的地面上放置小木块$m$,大木块$M$,左端是固定的墙壁,初始时刻$m$静止,$M$以初速度$v_{0}$向左运动,将与$m$发生碰撞,之后$m$获得速度向左运动,将与墙壁发生碰撞反弹,所有碰撞均没有动能损失,求碰撞次数。
图1
解析: 首先考虑最简单情况,若两滑块质量相等$m=M$,则$M$向左运动第一次与$m$碰撞,根据动量守恒和能量守恒,将发生速度传递,接下来$m$以$v_{0}$向左运动与墙壁第二次碰撞,速度反向向右,大小不变,之后向右运动,与$M$第三次碰撞,$m$停止,$M$以$v_{0}$向右运动。总碰撞次数为3。
接下来讨论滑块质量不相等的情况,设$M/m=k$,以水平向左为正方向,为了描述的需要,称两滑块之间的碰撞为碰撞,称$m$与墙壁的碰撞为反射,设第$n$次碰撞(包括反射)后,$m$与$M$速度分别为$u_{n}$和$v_{n} $,对第一次碰撞,根据动量守恒和能量守恒有
(1) $\begin{eqnarray} \left. {{\begin{array}{l} {mu_{1} +Mv_{1} =Mv_{0} }\\ {\dfrac{1}{2}mu_{1}^{2} +\dfrac{1}{2}Mv_{1}^{2} =\dfrac{1}{2}Mv_{0}^{2} }\\ \end{array} }} \right\} \end{eqnarray} $
(2) $\begin{eqnarray} \left. {{\begin{array}{l} {u_{1} =\dfrac{2k}{k+1}v_{0} } \\[2mm] {v_{1} =\dfrac{k-1}{k+1}v_{0} } \\ \end{array} }} \right\} \end{eqnarray} $
(3) $\begin{eqnarray} \left. {{\begin{array}{l} {u_{2} =-u_{1} } \\ {v_{2} =v_{1} } \\ \end{array} }} \right\} \end{eqnarray} $
第一次反射后,$m$将向右运动与$M$发生第二次碰撞,同样根据动量守恒和能量守恒
(4) $\begin{eqnarray} \left. {{\begin{array}{*{20}c} {mu_{3} +Mv_{3} =mu_{2} +Mv_{2} } \\ {\dfrac{1}{2}mu_{3}^{2} +\dfrac{1}{2}Mv_{3}^{2} =\dfrac{1}{2}mu_{2}^{2} +\dfrac{1}{2}Mv_{2}^{2} } \\ \end{array} }} \right\} \end{eqnarray} $
(5) $\begin{eqnarray} \left. {{\begin{array}{*{20}c} {u_{3} =\dfrac{(1-k)u_{2} +2kv_{2} }{k+1}} \\[2mm] {v_{3} =\dfrac{2u_{2} +(k-1)v_{2} }{k+1}} \\ \end{array} }} \right\} \end{eqnarray} $
将$u_{n}$,$v_{n} $写成向量$\left( {u_{n} \;v_{n} }\right)$,式(3)和式(5)可变为矩阵运算形式
(6) $\begin{eqnarray} \left\{ {{\begin{array}{*{20}c} {u_{2} } \\ {v_{2} } \\ \end{array} }} \right\}=\left[ {{\begin{array}{*{20}c} {-1} & 0 \\ 0 & 1 \\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} {u_{1} } \\ {v_{1} } \\ \end{array} }} \right\} \end{eqnarray} $
(7) $\begin{eqnarray} \left\{ {{\begin{array}{*{20}c} {u_{3} } \\ {v_{3} } \\ \end{array} }} \right\}=\frac{1}{k+1}\left[ {{\begin{array}{*{20}c} {1-k} & {2k} \\ 2 & {k-1} \\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} {u_{2} } \\ {v_{2} } \\ \end{array} }} \right\} \end{eqnarray} $
对比式(2)与式(7),发现式(2)也可以写为类似式(7)的样子
(8) $\begin{eqnarray} \left\{ {{\begin{array}{*{20}c} {u_{1} } \\ {v_{1} } \\ \end{array} }} \right\}=\frac{1}{k+1}\left[ {{\begin{array}{*{20}c} {1-k} & {2k} \\ 2 & {k-1} \\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} 0 \\ {v_{0} } \\ \end{array} }} \right\} \end{eqnarray} $
接下来第二次反射,第三次碰撞分别与式(3)和式(4)类似,只需将式(3)和式(4)中速度下标加1,因此结论也与式(6)和式(7)相似,因此每次碰撞和反射后,两滑块速度向量变换矩阵分别为
(9) $\begin{eqnarray} \frac{1}{k+1}\left[ {{\begin{array}{*{20}c} {1-k} & {2k} \\ 2 & {k-1} \\ \end{array} }} \right],\ \ \left[ {{\begin{array}{*{20}c} {-1} & 0 \\ 0 & 1 \\ \end{array} }} \right] \end{eqnarray} $
当两滑块碰撞后速度满足$v_{n} <0$ 且$\left| {u_{n} } \right|<\left| {v_{n} }\right|$时,碰撞将不再发生。
根据式(1)$\sim$式(9),作者编写了MATLAB函数文件,如图2 所示,利用该函数文件,计算了不同$k$值下的碰撞次数N_collide,如表1 所示。根据表1 数据,发现当$k=100^{N}$,N_collide与圆周率$\pi $的小数点后$N$位数字一样。
图2
2 理论证明
由表1 可以猜测,N_collide $=[(10^N)\cdot Pi]$,$[x]$为小于$x$的最大整数,接下来证明这个猜测。
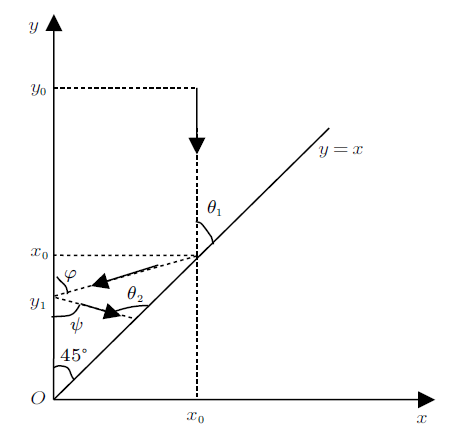
以水平面与墙壁交点为原点,水平向右为正方向,设初始时刻,$m$与$M$位置为$x_{0}$,$y_{0}$,$t$时刻$m$与$M$位置为$x(t)$,$y(t)$,根据图1
(10) $\begin{eqnarray} 0\leqslant x(t)\leqslant y(t) \end{eqnarray} $
当$x(t)=0$时,$m$与墙壁碰撞;当$x(t)=y(t)$时,$m$与$M$碰撞。如图3 所示,点$(x(t),y(t))$即可描述$t$时刻两滑块的位置,随着时间的推移,点$(x(t), y(t))$的移动形成位置相空间的轨迹图。第一次碰撞前,$m$位置不变,$M$向左运动,因此轨迹为竖直向下的直线,直至碰到直线$y=x$,发生碰撞,之后两滑块均向左运动,故$x(t)$,$y(t)$均减小,轨迹变为斜向下,直至$x(t)=0$,$m$与墙壁碰撞反射,反射后$m$速度反向,大小不变,因此在图像中有
(11) $\begin{eqnarray} \varphi =\psi \end{eqnarray} $
图3
之后,将发生第2次滑块间碰撞,反射$\cdots\cdots$。当第$n$次碰撞后,轨迹直线方向为斜向右上方,且接近与$y=x$平行时,将不再与$y=x$相交,即碰撞结束,轨迹与$y$轴、直线$y=x$交点个数之和为碰撞发生次数。由图3 可知
(12) $\begin{eqnarray} \theta_{1} =45^{\circ},\ \ \tan \varphi =u_{1} /v_{1},\ \ \theta_{2}=45^{\circ}+\varphi, \cdots \end{eqnarray} $
根据式(12)可以计算出碰撞次数,但计算有点繁琐,主要是因为式(12)中第二式涉及两滑块速度,而每次碰撞后,滑块速度均发生变化,为了计算的简单,接下来我们对相空间$(x(t),y(t))$ 作一个变形,使式(12)中第二式消失。
将$(x(t),y(t))$变形为$(X(t),Y(t))$,变换关系为
(13) $\begin{eqnarray} \left( {X\ \ Y} \right)=(x\ \ y)\left[ {{\begin{array}{*{20}c} {\sqrt m } & 0 \\ 0 & {\sqrt M } \\ \end{array} }} \right] \end{eqnarray} $
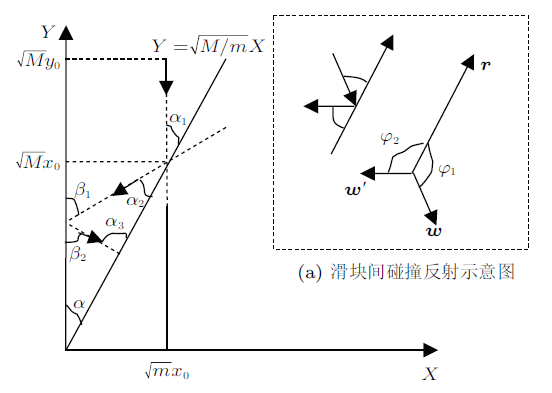
故$X(t)=\sqrt m x(t)$,$Y(t)=\sqrt M y(t)$,$X-Y$ 相空间轨迹如图4 所示,$x-y$ 相空间中的直线$y=x$变为$X-Y$中的$Y=\sqrt {{M}/{m}} X$,它与$Y$轴夹角为
(14) $\begin{eqnarray} \tan \alpha =\sqrt {\frac{m}{M}} \end{eqnarray} $
图4
当$m$与墙壁碰撞后,$m$速度反向,故图4 中$\beta_{1} =\beta_{2} $,当两滑块碰撞时,如图4 (a),$r$为直线$Y=\sqrt {{M}/{m}}x$方向向量$\left( {\sqrt m ,\sqrt M } \right)$,$w$为碰前入射向量$(\sqrt m u,\sqrt M v)$,${w}'$为碰后反射向量$(\sqrt m {u}',\sqrt M {v}')$,根据动量守恒,能量守恒式(4)可以改写为
(15) $\begin{eqnarray} \left. {{\begin{array}{l} r\cdot w=r\cdot {w}'={\rm cons1}\\ |w|=|w'| ={\rm cons2} \\ \end{array} }} \right\} \end{eqnarray} $
由式(15)可得入射向量$w$与$r$夹角同反射向量${w}'$与$r$夹角相等,即
(16) $\begin{eqnarray} \varphi_{1}=\varphi_{2} \end{eqnarray} $
(17) $\begin{eqnarray} \left.\begin{array}{l} \alpha_{1} =\alpha_{2} =\alpha\\ \beta_{1}=\alpha +\alpha_{2} =2\alpha\\ \alpha_{3}=\alpha +\beta_{2} =3\alpha\\ \qquad \quad \vdots \end{array}\right\} \end{eqnarray} $
由式(17)可知第$n$次碰撞前,轨迹方向与直线$Y=\sqrt {{M}/{m}}x$夹角为$n\alpha $,应满足条件
(18) $\begin{eqnarray} n\alpha <\pi \end{eqnarray} $
(19) $\begin{eqnarray} n=\left[ {\frac{\pi }{\alpha }} \right] \end{eqnarray} $
(20) $\begin{eqnarray} n=\left[ {\frac{\pi }{\arctan \sqrt {{m}/{M}} }} \right]=\left[ {\frac{\pi }{\arctan \sqrt {{1}/{k}} }} \right] \end{eqnarray} $
(21) $\begin{eqnarray} n=\left[ {\frac{\pi }{\arctan (10^{-N})}} \right] \end{eqnarray} $
将$\arctan x$在$x=0$ 附近作泰勒展开可得
(22) $\begin{eqnarray} \arctan x=x-\frac{x^{3}}{3}+\frac{x^{5}}{5}-\frac{x^{7}}{7}+\cdots \end{eqnarray} $
(23) $\begin{eqnarray} &&\dfrac{1}{\arctan x}-\dfrac{1}{x}=\dfrac{x-\arctan x}{\arctan x\cdot x}=\\&&\qquad \dfrac{\dfrac{1}{3}x^{3}-\dfrac{1}{5}x^{5}+\dfrac{1}{7}x^{7}-\cdots}{x\left( {x-\dfrac{1}{3}x^{3}+\dfrac{1}{5}x^{5}-\cdots} \right)}= \\&&\qquad x\dfrac{\dfrac{1}{3}-\dfrac{1}{5}x^{2}+\dfrac{1}{7}x^{4}-\cdots}{1\mbox{-}x^{2}\left( {\dfrac{1}{3}-\dfrac{1}{5}x^{2}+\cdots} \right)} \end{eqnarray} $
$\begin{eqnarray*} \lim\limits_{x\to 0} \left( {\frac{1}{\arctan x}-\frac{1}{x}} \right)=0,\ \ 0<\frac{1}{\arctan x}-\frac{1}{x}<x \end{eqnarray*}$
因此式(21)变为$n=\left[ {\pi \cdot 10^{N}} \right]$ 。
3 结语
本文通过MATLAB计算了滑块碰撞次数,发现当$k=100^{N}$,碰撞次数为$[\pi \times 10^{N}]$,即碰撞次数与圆周率小数点后数字一样,并利用相空间轨迹法巧妙地证明了该联系。将力学过程用几何图像表示出来有助于清晰理解整个运动过程,使计算变得简化。
参考文献
View Option
[1]
鞠实儿 , 张一杰 . 刘徽和祖冲之曾计算圆周率的近似值吗? 中国科技史杂志 , 2019 (4 ):389 -401
[本文引用: 1]
Ju Shi'er Zhang Yijie . Did Liu Hui and Zu Chongzhi compute the approximation of $\pi$
The Chinese Journal for the History of Science and Technology 2019 (4 ):389 -401 (in Chinese)
[本文引用: 1]
[2]
Mikami Y The Development of Mathematics in China and Japan . New York : Chelsea Publishing Company , 1913
[本文引用: 1]
Did Liu Hui and Zu Chongzhi compute the approximation of $\pi$
1
2019
... 滑块碰撞是牛顿力学中常见的问题,一般通过动量守恒和能量变化的关系去研究碰撞过程;而圆周率$\pi$是几何数学的问题,为圆的周长与直径之比,历史上我国数学家刘徽通过割圆术算出$\pi$的小数点后第5位3.14159,之后数学家们计算出的小数点后位数越来越多[1 -2 ] .$\pi$的数字为:3.14159265358979323846264338327950288419716939937510$\cdots$,滑块碰撞与 这两者看起来毫无联系,但有趣的是,作者在研究碰撞问题时,发现滑块的碰撞次数与$\pi$极其相似,并分析了它们的内在关联. ...
Did Liu Hui and Zu Chongzhi compute the approximation of $\pi$
1
2019
... 滑块碰撞是牛顿力学中常见的问题,一般通过动量守恒和能量变化的关系去研究碰撞过程;而圆周率$\pi$是几何数学的问题,为圆的周长与直径之比,历史上我国数学家刘徽通过割圆术算出$\pi$的小数点后第5位3.14159,之后数学家们计算出的小数点后位数越来越多[1 -2 ] .$\pi$的数字为:3.14159265358979323846264338327950288419716939937510$\cdots$,滑块碰撞与 这两者看起来毫无联系,但有趣的是,作者在研究碰撞问题时,发现滑块的碰撞次数与$\pi$极其相似,并分析了它们的内在关联. ...
1
1913
... 滑块碰撞是牛顿力学中常见的问题,一般通过动量守恒和能量变化的关系去研究碰撞过程;而圆周率$\pi$是几何数学的问题,为圆的周长与直径之比,历史上我国数学家刘徽通过割圆术算出$\pi$的小数点后第5位3.14159,之后数学家们计算出的小数点后位数越来越多[1 -2 ] .$\pi$的数字为:3.14159265358979323846264338327950288419716939937510$\cdots$,滑块碰撞与 这两者看起来毫无联系,但有趣的是,作者在研究碰撞问题时,发现滑块的碰撞次数与$\pi$极其相似,并分析了它们的内在关联. ...